装载机线控转向系统的设计与分析

， 　，

(四川大学 制造科学与工程学院， 四川 成都　610065)

引言

装载机转向系统在使用时主要存在以下问题：系统主要为节流和溢流控制，能量损耗大；方向盘与转向系统连接复杂造成驾驶室工作环境差；驾驶员驾驶易疲劳。

针对以上缺点，设计了线控转向系统，该系统充分利用了电子和液压技术，采用ECU作为系统的控制核心，利用传感器采集的数据，在ECU处实时比较，实现了装载机的准确转向。ECU作为控制中心可以在特点算法下处理一些情况，可以减轻驾驶员的劳动强度，另外本设计采用变量泵作为供油元件，变节流控制为容积控制，具有较好的节油性。

1　系统设计

如图1所示，线控转向系统主要由比例控制变量泵、方向盘、转向马达和电磁换向阀等组成。其中比例控制变量泵由三通比例阀、变量活塞和变量反馈杆以及变量泵组成。当系统工作时，首先由ECU发出信号控制三通比例阀，输入的电流所产生的电磁力使三通比例阀产生一个与输入电流成正比的开度，这样先导液压油通过打开的阀口进入变量活塞的无杆腔，变量活塞杆产生位移，使泵的排量增加，活塞杆位移通过反馈杆作用在三通比例阀的阀套上，使阀套移动，直到将刚才打开的阀口关闭，阀芯重新进入一个平衡状态，此位置对应泵的一个排量值，变量泵的排量与输入三通比例阀的电信号大小成比例关系。转向马达的转角通过转角传感器将转向角度信号传递到ECU，ECU将马达转角信号与方向盘转角信号进行比较，若比较结果为零，则ECU控制系统停止转向；若不为零，则ECU控制转向系统调整，直至停止转向。

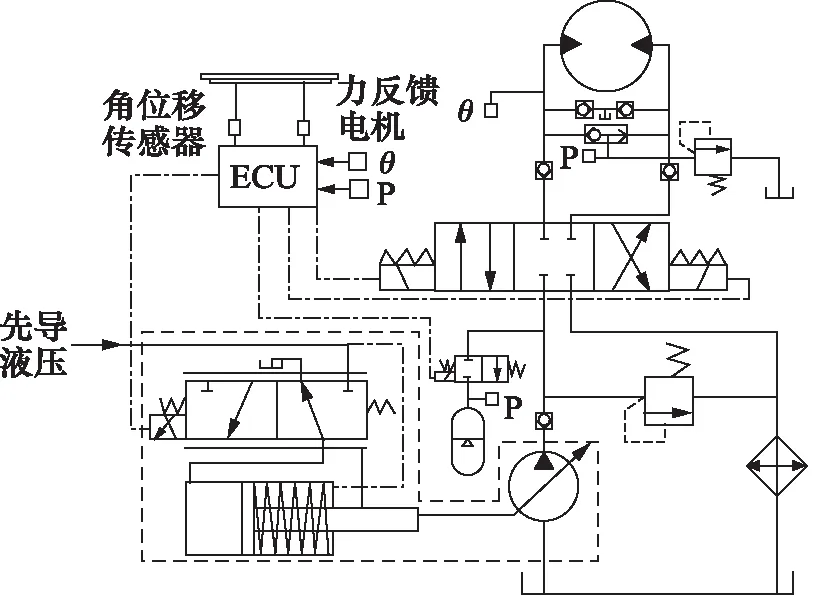
图1　线控转向系统原理图

2　系统数学模型

2.1　三通比例阀数学模型[1]

三通比例阀的传递函数为：

(1)

其中，Kbv—— 比例阀的增益系数

ξbv—— 比例阀液压阻尼系数

ωbv—— 比例阀液压固有频率

2.2　三通比例阀控制变量油缸

三通比例阀从本质上来说是1个二位三通阀，因此三通比例阀控制变量油缸可以简化为三通阀差动控制压缸的数学模型。于是可有三通比例阀控制变量油缸的数学模型为[2]：

(2)

其中，Kq—— 液压弹簧刚度

ωh—— 液压固有频率

ξh—— 液压阻尼比

2.3　变量油缸控制变量泵传递函数[2]

变量油缸控制变量泵的传递函数为：

(3)

其中，L—— 活塞施力点与斜盘底面距离

2.4　变量泵控制转向马达数学模型

液压马达转角对变量泵斜盘倾角的传递函数为：

(4)

液压马达转角对外负载的传递函数为：

(5)

其中，Kp—— 变量泵的排量梯度

r—— 变量泵斜盘倾角

ωh—— 液压固有频率

ξh—— 液压马达液压阻尼比

2.5　角位移传感器数学模型

角位移传感器是用来探测转向马达的转角，并将转角信号与方向盘转角进行比较，以此来确定转向的准确性。

角位移传感器的动态响应很高，可以视为一阶比例环节，其传递函数为：

Kθ=U(s)/θm(s)

(6)

2.6　放大器建模

放大器为比例环节，其传递函数为：

KF=I(s)/U(s)

(7)

2.7　方向盘转角与转速传递函数

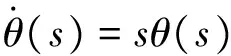
(8)

2.8　传递函数化简

在泵控马达系统中，由于泵控马达环节的动态远低于比例阀控制变量油缸环节的动态，因此忽略阀控液压缸环节，此时比例阀可以简化为比例环节[3]，所以，比例阀的传递函数可以简化为：

(9)

比例阀控制变量油缸的环节可以简化为一个比例环节和一个积分环节[5]，所以阀控液压缸环节可以简化为：

(10)

2.9　系统控制方框图

根据设计要求，方向盘的转角要与转向油缸活塞杆伸缩量成比例关系，方向盘转速要与变量泵排量成比例关系，因此其传递函数方框图如图2、图3所示。

图2　线控转向系统执行系统控制方框图

图3　简化控制方框图

3　系统的PID模糊控制

PID模糊控制是PID控制技术与模糊控制技术的产物，PID控制可以方便地调节系统的震荡、超调和延迟等，模糊控制特别适用于难以获得精确数学模型的系统，例如装载机转向过程中，由于路面和负载的变化的不确定性，转向负载难以精确量化，模糊控制给了我们最优的选择。

本设计的PID模糊控制是增量式模糊控制，通过在已有的PID参数基础上加上装载机转向角度误差的模糊控制输出，最终对转向系统进行控制矫正。其控制公式为：

(11)

(12)

(13)

误差e和误差变化ec的基本论域为:

e，ec={-5,-4,-3,-2,-1,0,1,2,3,4,5}。

ΔKp=[0,0.1]，ΔKi=[0,0.01]，

ΔKd=[0,0.001]；模糊子集为：

e,ec={NB,NM,NS,ZO,PS,PM,PB}；

ΔKp,ΔKi，ΔKd={NB,NM,NS,ZO,PS,PM,PB}。

NB——负大，NM——负中，NS——负小，ZO——零，PS——正小，PM——正中，PB——正大。

本设计的采集误差为方向盘转角与液压缸活塞杆位移的伸缩量之间的差值，对应的意义如下：

NB——差值为负值，且很大；NM——差值为负值，且较大；NS——差值为负值，且较小；PB——差值为正，且很大；PM——差值为正，且较大；PS——差值为正，且较大；ZO——差值为零。

模糊控制规则如表1～表3所示。

表1　ΔKp的模糊控制规则表

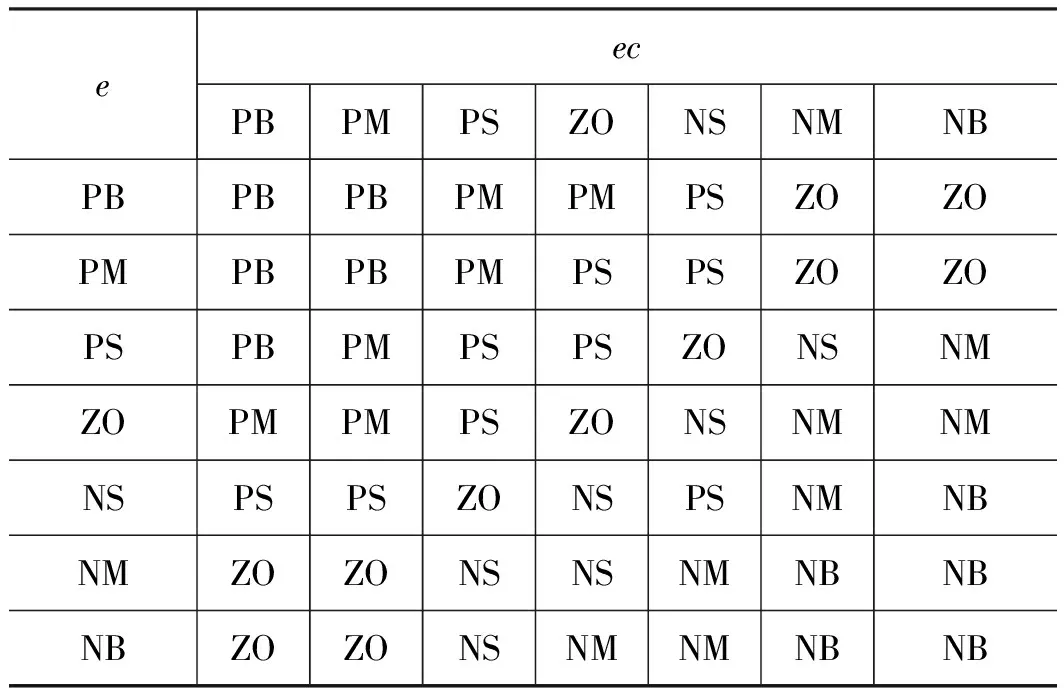
表2　ΔKi模糊控制规则表

图4　模糊控制方块图

eecPBPMPSZONSNMNBPBPBPSPSPMPMPMPBPMPBPSPSPSPSNSPMPSZOZOZOZOZOZOZOZOZONSNSNSNSNSZONSZONSNSNMNMNSZONMZONSNMNMNBNSPSNBPSNMNBNBNBNSPS

于是建立PID 模糊控制模型如图4、图5所示。

4　参数计算

误差量化因子：

(14)

误差变化量化因子：

(15)

ΔKp的量化因子：

(16)

ΔKi的量化因子：

(17)

ΔKd的量化因子：

(18)

表4是系统仿真参数表。

表4　执行系统参数表

5　系统仿真

在系统稳定工作在15 MPa时，设定以下仿真情形：

(1) 在阶跃信号作用下加入单位阶跃干扰信号的情况；

(2) 在输入正弦信号作用下，突然在1 s加入阶跃信号，其幅值为100(轻干扰)；

(3) 在输入正弦信号作用下，突然在1 s加入阶跃信号，其幅值为500(中干扰)；

(4) 在输入正弦信号作用下，突然在1 s加入阶跃信号，其幅值为1000(重干扰)。

图6～图9为在各种情况下的仿真图形。

图5　PID模糊控制系统仿真图

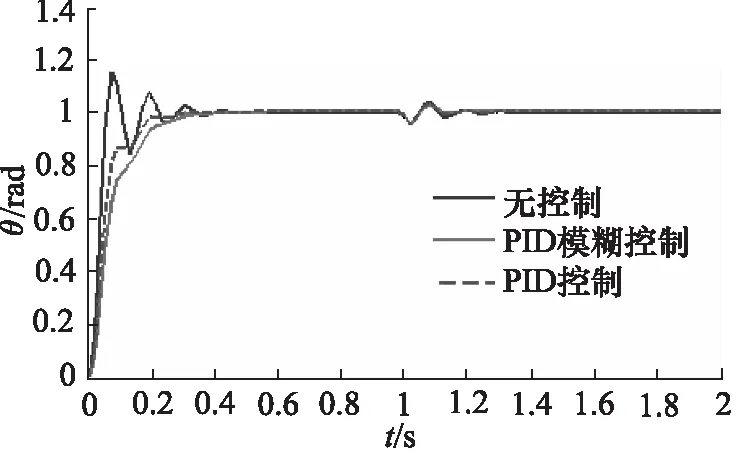
图6　单位阶跃干扰仿真图

图7　轻微干扰仿真图

图8　中度干扰仿真图

图9　重度干扰仿真图

6　结论

从以上图形可知，当系统在不同干扰存在的情况下，系统可以根据控制策略自动调整，仿真表明，PID模糊控制较PID控制和无控制稳定时间更快，震荡更小，超调更小。PID模糊控制应用于线控转向系统的控制系统是具有良好的稳定性和灵敏性，完全满足线控转向的要求。

参考文献：

[1]罗小梅.电液比例泵控马达控制系统的分析研究[D].西安：长安大学，2005．

[2]王春行.液压控制系统.机械工业出版社[M].北京：机械工业出版社，1999.

[3]李寿刚．液压传动[M]．北京：北京理工大学出版社，1993．

[4]卢长庚．液压控制系统的分析与设计[M]．北京：煤炭工业出版社．1991

[5]张磊,史小辉,许明恒,等.隧道挖掘装载机液压系统关键技术研究[J].液压与气动,2011,(5):10-12.

[6]刘增辉,杜长龙.连续式液压装载机闭式回路液压系统设计[J].液压与气动,2012,(5):16-20.