长管拖车复合材料气瓶内胆点蚀处剩余壁厚的研究

王静娴，邓贵德，段滋华，梁海峰(.太原理工大学化学化工学院，山西太原　03004; .中国特种设备检测研究院，北京　0003 )

长管拖车复合材料气瓶内胆点蚀处剩余壁厚的研究

王静娴1，邓贵德2，段滋华1，梁海峰1
(1.太原理工大学化学化工学院，山西太原030024; 2.中国特种设备检测研究院，北京100013 )

摘要:采用有限元软件ANSYS对气瓶内壁存在不同尺寸凹坑缺陷的环缠绕复合材料气瓶及全金属气瓶在各载荷步下进行了计算，其中应用了单元生死技术来控制凹坑出现的时间。基于Goodman平均应力修正方程，计算复合气瓶有点蚀凹坑相对于无点蚀凹坑的等效交变应力幅增量，并与钢制气瓶有点蚀凹坑相对于无点蚀凹坑的等效交变应力幅增量进行比较。计算结果表明，点蚀处剩余壁厚为75%的设计壁厚对于复合材料气瓶来说偏于保守，认为复合材料气瓶点腐蚀处剩余壁厚不得小于设计壁厚的50%较为合理。

关键词:长管拖车复合材料气瓶;点蚀;有限元分析;单元生死

0　引言

长管拖车气瓶作为一种高效的运输设备，被广泛地应用于天然气、氢气等气体的运输中。由于复合材料气瓶质量轻、强度高，有望逐渐取代钢瓶成为长管拖车气瓶市场应用的主流［1-2］。就长管拖车全金属气瓶检验案例来看，腐蚀是目前最常见的问题之一。纤维缠绕复合材料气瓶在工作过程中，由于介质腐蚀的原因，内胆内壁也会出现腐蚀，这会严重影响其抗疲劳性能。我国TSG R7001—2013《压力容器定期检验规则》附录D《长管拖车、管束式集装箱定期检验专项要求》中对钢制长管拖车气瓶内部凹坑深度做了明确规定:点腐蚀剩余壁厚不得小于设计壁厚的75%［3］。为验证此值是否可以直接应用在复合材料长管拖车气瓶的定期检验中，作者采用ANSYS有限元软件，对工作压力为20 MPa、内壁存在点蚀缺陷的钢制长管拖车气瓶和环缠绕复合材料长管拖车气瓶进行了应力分析。采用Goodman［4-5］平均应力修正方程，对计算所得疲劳应力幅进行了等效处理，基于等效疲劳应力幅对环缠绕气瓶的抗疲劳性能进行对比分析。

1　单元生死技术

复合气瓶内胆内壁的点蚀凹坑出现在工作过程中，认为气瓶在自增强过程及出厂时零压力下是无缺陷的。这时希望“杀死”点蚀凹坑模型内的所有单元。在这种情况下，可以在模型加载过程中的某一指定时间(载荷步)利用单元的生与死选项来杀死或重新激活选定的单元。

单元生死选项并非真正删除或重新加入单元。要激活“EKILL”的效果，ANSYS程序只是将其刚度(或传导，或其他分析特性)矩阵乘以一个很小的因子［ESTIF］，默认值为1.0×10－6。死单元的单元载荷将为0，从而不对载荷向量生效。同样，死单元的质量、阻尼、比热和其他类似效果也设为0。死单元的质量和能量将不包括在模型求解结果中。单元的应变在“杀死”的同时也被设为0。同样的，如果单元“出生”，并不是将其加到模型中，而是重新激活它们。要“加入”一个单元，先杀死它，然后在合适的载荷步中重新激活它［6］。

2　数值计算

2.1物理模型

采用的长管拖车钢制气瓶及复合气瓶结构尺寸如图1(a)、(b)所示，其工作压力为20 MPa、公称直径为Φ559 mm、总长为5 m，金属气瓶设计壁厚为16.5 mm，复合材料气瓶内胆壁厚为7.4 mm、内胆外用玻璃纤维环氧树脂材料缠绕30层，总厚度为11 mm。对于复合材料气瓶，气瓶在投入使用前要进行自增强处理，自紧压力为32 MPa。

考虑到模型、载荷和约束的对称性，以及点蚀凹坑相对于整体尺寸较小，影响范围不大，取整体模型的八分之一建模，模型切面建立对称约束。作者建立了钢制带点蚀凹坑及复合材料带点蚀凹坑两种气瓶模型，从气瓶靠近封头开始向气瓶中部，以530 mm为间隔，各建立4个点蚀凹坑位于不同位置的模型，如图1所示，从靠近封头开始记r个位置为位置1、2、3、4。钢制气瓶点蚀凹坑深度z取气瓶定期检验标准中规定的最大深度，即25%设计壁厚;复合材料气瓶模型点蚀凹坑深度z除25%设计壁厚外，又以5%为增量建立变化范围为30%～55%的带点蚀凹坑模型。为了与无缺陷气瓶作对比，又建立了无缺陷的钢制模型和复合材料气瓶模型，共建立了34个模型。

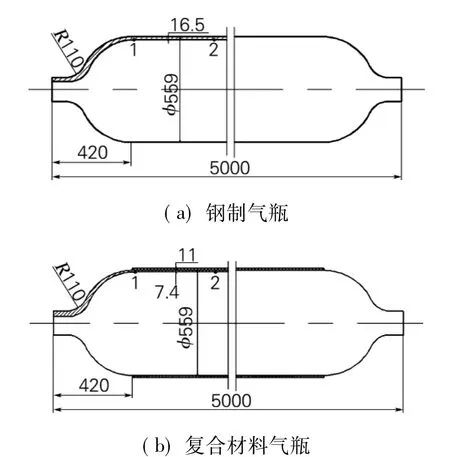
图1　物理模型结构示意图Fig.1　Schematic diagram of the structure of the physical model

对于点腐蚀，点蚀凹坑深度越深，半径越小，应力集中越明显［7］。点腐蚀深度通常都小于孔径。为使计算结果适于最不利情况，假设气瓶内壁点蚀凹坑为半球形，即半径等于深度。通过布尔运算，用球面切割内胆得到凹坑，如图2所示为靠近封头处的凹坑模型。

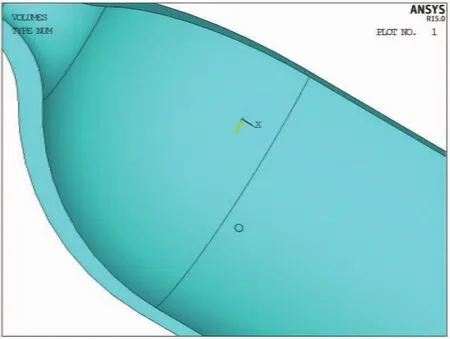
图2　凹坑的钢制气瓶模型Fig.2　A pit defect on a steel cylinder

2.2网格划分

作者采用ANSYS软件进行有限元建模和分析［8-9］。划分网格时，钢制及复合材料气瓶筒体轴向单元长度20 mm，封头轴向单元长度10 mm，钢制气瓶和复合材料气瓶内胆壁厚方向保持为3层单元，凹坑部分采用四面体自由划分，其余部分采用8节点的Solid185进行扫掠网格划分。复合材料气瓶内胆筒体段外表面采用Shell181单元生成面网格，并通过面网格截面属性来设置缠绕层厚度、层数和角度。图3所示为建立的环缠绕复合气瓶整体网格模型，金属气瓶的网格模型除了没有缠绕层外，与复合材料气瓶内胆相似。

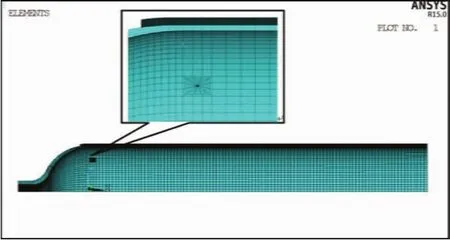
图3　复合材料气瓶网格模型Fig.3　Finite element mesh of the composite cylinder

2.3材料模型

内胆材料30CrMo的弹性模量为206 GPa，泊松比为0.3，实测屈服强度为657.1 MPa、抗拉强度为766.0 MPa，真实应力应变曲线参见文献［10］。有限元计算中内胆材料采用多段线性等向强化模型描述。缠绕层采用碳纤维材料，用线弹性正交各向异性材料模型描述，详细参数如表1所示。

表1　缠绕层材料参数Tab.1 Material parameters of the winding layer

2.4载荷与边界条件

通常情况下，认为气瓶出厂时不存在缺陷，因此，复合气瓶在自紧压力及完全卸载2个载荷步不出现点蚀凹坑缺陷。气瓶出厂后，气瓶的充放气过程用第3、4个载荷步，即工作压力和放气后零压力。在第3个载荷步分析之前，通过单元生死处理，杀死点蚀凹坑处部分单元，将点蚀凹坑“挖出”，并将内压载荷施加于点蚀凹坑表面，再进行计算。表2为4个载荷步下的内压p和瓶口等效拉应力σ。

表2　载荷设置Tab.2 Load applied

3　结果与讨论

3.1钢制气瓶模型计算结果分析

(1)钢制气瓶无缺陷时，工作压力20 MPa下应力分布如图4(a)所示，最大环向应力出现在筒身段，为333.2 Mpa;

(2)模型在充放气循环中应力在0～333.2 MPa变化，交变应力幅为166.6 MPa，平均应力为166.6 MPa;

(3)钢制气瓶存在凹坑时，工作压力20 MPa下应力分布如图4(b)所示，凹坑处出现明显的应力集中，凹坑处最大应力为453.3 MPa，其余部分受力均匀，与无缺陷模型应力分布一致。经计算，凹坑位于其余3个位置的最大应力依次为518.1，509.2，512.1 MPa。

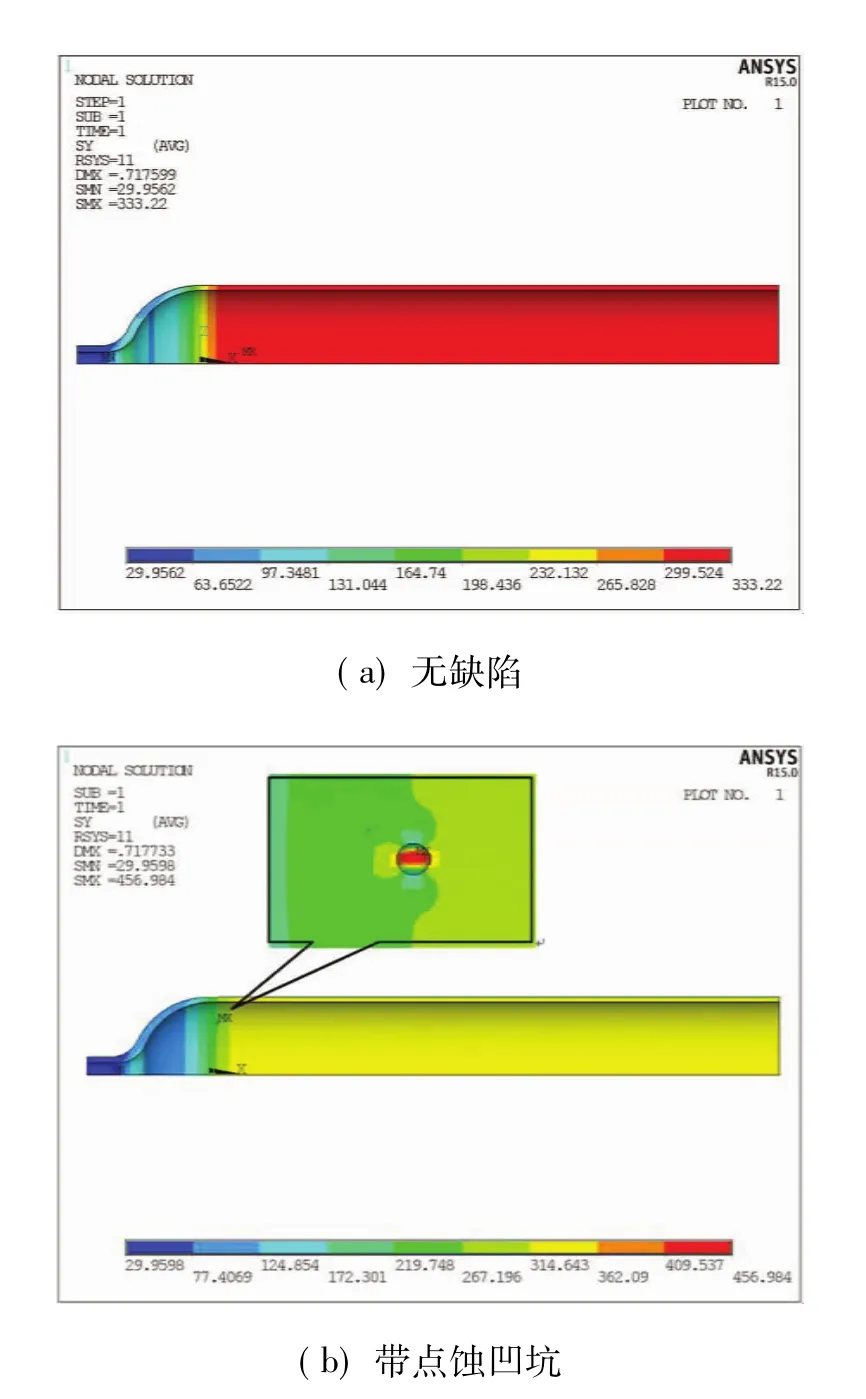
图4　钢制气瓶模型工作压力下的环向应力Fig.4　Hoop stress of the steel cylinder under working pressure

对于不同平均应力下的不同疲劳交变应力幅值，可基于Goodman平均应力修正方程，按照等寿命原则转化为平均应力为零时的等效交变应力幅［4］。基于Goodman方程的等效交变应力幅计算公式为:式中: Sar为平均应力为零时的等效交变应力幅，Sa为平均应力为Sm时的交变应力幅，Rm为材料抗拉强度，本文取内胆实测屈服强度值657.1 MPa。

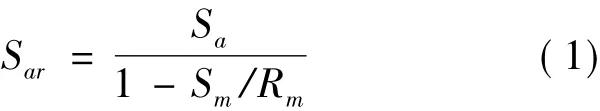
经计算，基于Goodman方程，4个带点蚀凹坑钢制气瓶的等效交变应力幅分别比无点蚀凹坑时增大了55.60%，97.78%，86.25%，87.97%。位置1处的交变应力幅值受封头的约束影响，明显低于其余3个位置应力幅值;位置2、3、4的应力幅值差距较小。

3.2复合材料气瓶模型计算结果

复合材料气瓶计算分4个分析步，在气瓶充放气过程中，气瓶的应力幅为第3、4分析步的差值，通过是否进行单元生死来模拟点蚀凹坑是否存在。

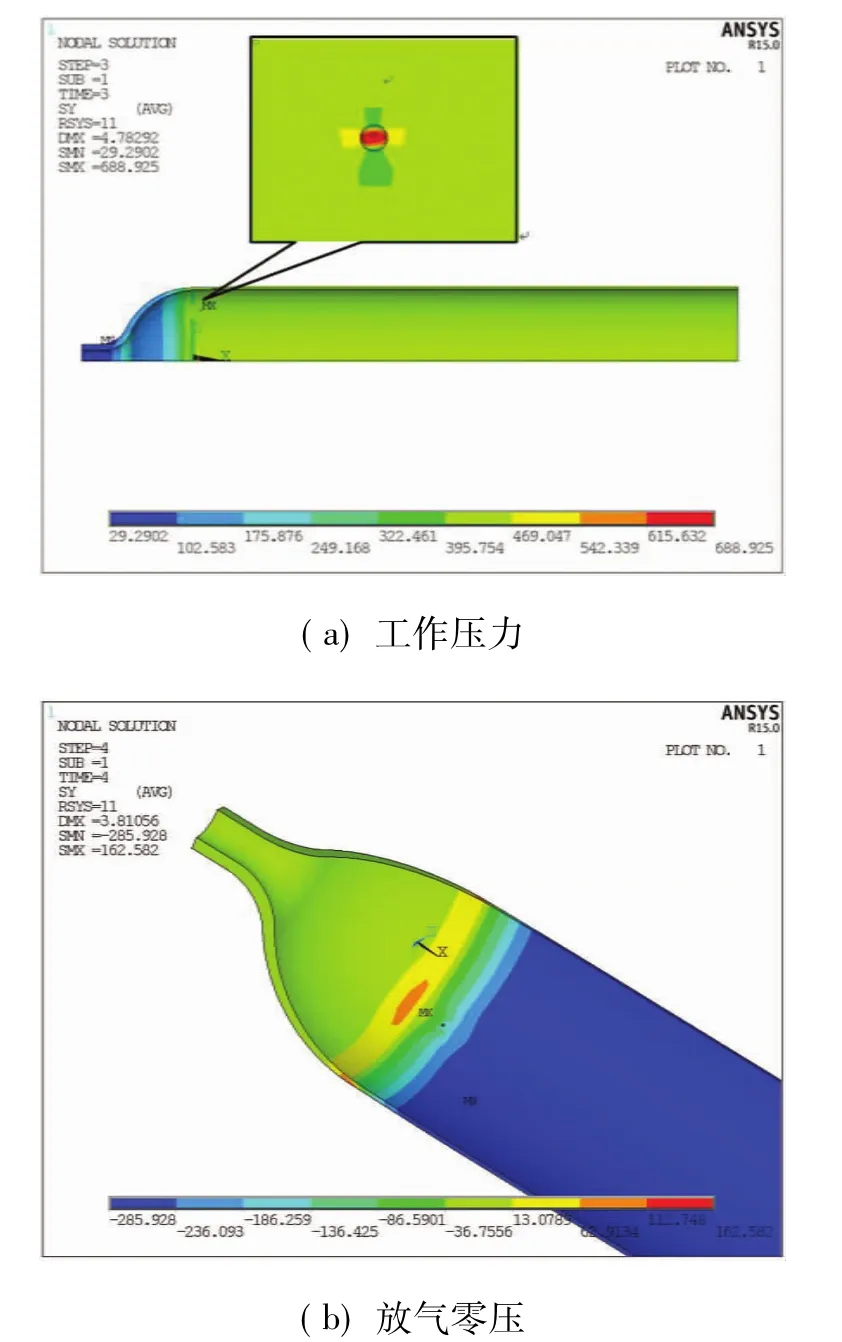
图5　复合材料气瓶带点蚀凹坑1的环向应力Fig.5　The composite cylinder with a pit defect at location 1 under working pressure

通过对无缺陷复合材料气瓶有限元模型计算，在零压下和工作压力下的最大压应力和拉应力分别为－285.9和532.2 MPa，应力幅为409.0 MPa，平均应力为123.1 MPa;图5所示的是复合材料气瓶在凹坑部分单元被杀死后，工作压力及放气为零压下的应力分布。图5(b)可以看出，气瓶放气后，点蚀凹坑处非气瓶最大压应力发生处，最大压应力的位置及数值不受点蚀凹坑存在的影响，最大压应力为－285.9 MPa，所以可以直接用分析步2的结果来代替气瓶使用过程中放气为零压力下的最大压应力值。工作压力下点蚀凹坑处出现明显的应力集中，点蚀凹坑位于位置1的复合气瓶模型最大环向拉应力为688.9 MPa，此时交变应力幅为487.4 MPa，平均应力为201.5 MPa。点蚀凹坑位于其余3个位置的模型零压下最大压应力及工作压力下最大拉应力分别为－285.0/680.5，－285.6/689.2，－285.8/689.6 MPa可以看出，点蚀凹坑的存在增高了气瓶工作过程中的应力幅和最大应力。

经计算，基于Goodman方程，4个有点蚀凹坑模型与无点蚀凹坑相比，等效交变应力幅分别增大了39.66%，39.25%，39.28%，39.32%。计算结果均小于点蚀凹坑位置相对应的全金属气瓶等效交变应力幅的增量，所以可以认为点蚀处剩余壁厚为75%的设计壁厚对于复合材料气瓶来说较为保守，可以适当降低。

3.3复合材料气瓶在不同凹坑深度下的等效交

变应力幅增量

计算了其余6个不同点蚀凹坑深度下，点蚀凹坑位于4个位置上的复合材料气瓶模型。得到压、拉应力最值后，基于Goodman方程计算出等效交变应力幅，并算出与无缺陷相比的增量。最后得到图6所示的折线图。图例中的百分比为点蚀凹坑深度相对于钢制气瓶或复合材料的钢制内胆设计壁厚的百分比。

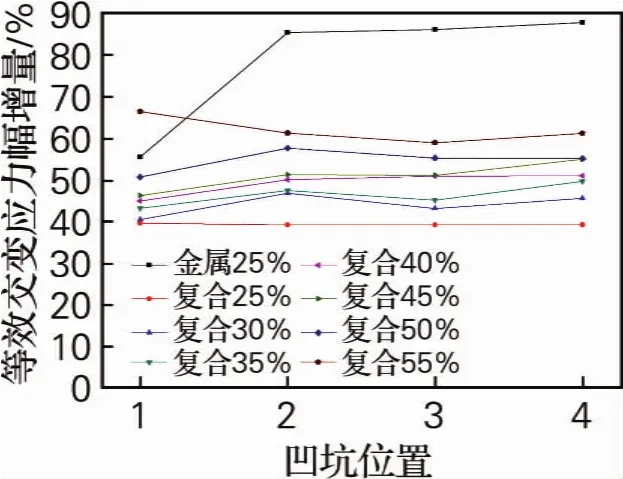
图6　全金属气瓶和复合气瓶在不同凹坑位置下等效交变应力幅增量Fig.6　The incremental of the equivalent alternating stress amplitude in the steel cylinders and the composite cylinders with pit defect at different location

由图6可以看出，同样点蚀凹坑深度下，钢制气瓶点蚀凹坑位置对其疲劳寿命的影响较大，在靠近封头处的点蚀凹坑对钢制气瓶疲劳影响最小;而复合材料气瓶点蚀凹坑位置对其疲劳寿命影响较小，但复合材料气瓶的点蚀凹坑越深，点蚀凹坑处应力集中越明显，对气瓶的寿命影响也就越大。

复合材料气瓶中点蚀凹坑深度在内胆设计壁厚的25%时，其交变应力幅增量远远小于钢制气瓶在凹坑深度为25%设计壁厚时的交变应力幅增量。复合材料气瓶的点蚀凹坑深度越大，其交变应力幅增量越大，在位置1处，复合材料气瓶点蚀凹坑深度为55%设计壁厚模型的等效交变应力幅增量超过钢制气瓶点蚀凹坑深度25%模型，其余值均小于钢制气瓶模型的等效交变应力幅增量值。故认为缠绕层起到保护钢制内胆的作用，使其受点蚀凹坑的影响减小。凹坑深度为25%，即点蚀凹坑处剩余壁厚75%的设计壁厚对于复合材料气瓶来说较为保守，由图6可见，点蚀凹坑深度可以增加到50%，即点蚀凹坑处剩余壁厚可以降低到50%。

4　结论

(1)点蚀凹坑的存在对两种长管拖车气瓶工作压力下的应力分布有明显影响。以点蚀凹坑位于位置1为例，带点蚀凹坑钢制气瓶的最大应力比无缺陷钢制气瓶最大应力增加了36.38%;复合气瓶点蚀凹坑深度越大，应力集中越明显，对气瓶的疲劳寿命影响越大，基于Goodman方程，点蚀凹坑位于位置1模型剩余壁厚均为设计壁厚的75%的等效交变应力幅增量分别55.605%和39.662%。对于点蚀凹坑来说，复合材料气瓶内胆上的凹坑越深，对疲劳影响越大，点蚀凹坑位于位置1剩余壁厚为设计壁厚的75%，70%，65%，60%，55%，50%，45%对应的等效交变应力幅增量为39.662%，40.52%，43.26%，45.03%，46.35%，50.82%，66.52%。

(2)对于钢制气瓶，点蚀凹坑靠近封头时，受封头的影响，气瓶的交变应力幅值明显低于其余位置;对于复合材料气瓶，由于纤维层的约束，点蚀凹坑在靠近封头时几乎不受封头影响。

(3)把钢制气瓶定期检验标准中规定的点腐蚀处剩余壁厚不得小于设计壁厚的75%应用在复合材料定期检测中较为保守，可以适量的降低该百分比。通过数值模拟，认为复合材料气瓶点腐蚀处剩余壁厚不得小于设计壁厚的50%较为合理。

参考文献:

［1］周海成，阮海东.纤维缠绕复合材料气瓶的发展及其标准情况［J］.压力容器，2004，21(9) :32-36.

［2］白金亮.铝内胆碳纤维缠绕气瓶及定期检验［J］.中国特种设备安全，2009，25(11) :21-24.

［3］中华人民共和国国家质量监督检查检疫总局.TSG R 7001—2013压力容器定期检验规则［S］.北京:中国计量出版社，2013.

［4］郑津洋，董其伍，桑芝富.过程设备设计［M］.2版.北京:化工出版社，2005:206-210.

［5］KWOFIE S.An exponential stress function for predicting fatigue strength and life due to mean stresses［J］.International Journal of Fatigue，2001，23 (9) : 829-836.

［6］段成红，吴祥，罗翔鹏.碳纤维缠绕复合气瓶爆破压力的有限元分析［J］.玻璃钢/复合材料，2012(2) : 17-39.

［7］DENG Guide，LI Qingwan，SUN Liang，et al.Fatigue performance analysis of hoop-wrapped composite cylinders with pit defects on liner based on element birth and death method［C］//Proceedings of the ASME 2014 Pressure Vessels and Piping Conference.Anaheim: A-merican Society of Mechanical Engineers，2014: V001T01A084.

［8］李玮，段成红，吴祥.碳纤维复合材料强度的有限元模拟［J］.玻璃钢/复合材料，2011(1) :20-23.

［9］郭亚芳.CNG复合材料缠绕气瓶自紧压力的优化［J］.玻璃钢/复合材料，2013(3) :62-65.

［10］张宗毅，邓贵德，寿比南，等.缠绕张力对环缠绕复合材料气瓶应力的影响［J］.压力容器，2011，28 (5) :7-14.

Research on remaining wall-thickness at pitting of the liners of hoop-wrapped composite cylinders for tube trailers

WANG Jingxian1，DENG Guide2，DUAN Zihua1，LIANG Haifeng1
(1.School of Chemistry and Chemical Engineering，Taiyuan University of Technology，Taiyuan 030024，China; 2.China Special Equipment Inspection and Research Institute，Beijing 100013，China )

Abstract:Finite element method was used to analyze the stress of hoop-wrapped composite cylinders or steel cylinders with pit defects of different sizes，in which the time of pit appearance was determined by element birth and death method.The incremental of the equivalent alternating stress amplitude in composite cylinder with pits against no pits was calculated based on Goodman stress correction equation，and compared with the increments of the seamless steel cylinder.Numeral results suggested that to set the remaining wall thickness as 75% of the design of wall thickness is more conservative for composite cylinders.The percentage can be reduced properly，and 50% is suitable.

Key words:tube trailers with hoop-wrapped composite cylinders; pit; finite element analysis; element birth and death method

作者简介:王静娴(1988-)，女，硕士研究生;通信作者:邓贵德(1982-)，男，高级工程师.

基金项目:国家公益性行业(质检)科研专项项目(201210020).

收稿日期:2014-10-29.

文章编号:1674-1404(2015) 03-0191-05

中图分类号:TQ053.2

文献标志码:A