DHMM在机械设备音频识别中的应用

苏 鹏，程 健

中国科学技术大学 自动化系，合肥 230027

1 引言

随着自动化、计算机、通信技术的发展，监控行业近年来技术不断更新，应用领域逐渐扩展。传统监控方式主要以视频信号作为信息的载体，辅以音频等多媒体信号作为补充。然而，对于机械设备而言，基于视频的监控存在固有的缺点，表现在：（1）视频监控易受到监控环境的光照条件的影响。（2）视频监控需要安装摄像机，对于很多机械设备，摄像机无法拍摄机器内部的运转情况。（3）基于视频的监控系统一般离不开人脑的主观判断而分析现场信息，很难做到高度的自动化和智能化。针对视频监控的不足，以音频信号作为信号载体，可以克服环境光照等因素的影响，反应现场设备工作时内部运转情况，从而大大提高设备控制的自动化、智能化。音频监控主要有三种用途：一是可以远程监控现场设备运行状态；二是可以用于远程故障诊断；三是可以用于特定区域的目标识别。

隐Markov模型（Hidden Markov Models，HMM）作为一种统计模型，广泛应用于语音处理的各个方面，它的理论基础是在1970年前后由Baum等人建立起来的[1-2]，随后由CMU的Baker和IBM的Jelinek等人将它应用于语音识别中[3]。由于Bell实验室Rabiner等人在80年代中期对HMM的深入浅出的介绍[4-5]，才逐渐使HMM为世界各国语音研究人员所熟悉。随后，HMM的应用领域不断扩大，在手写字识别[6]、手势识别[7]、旋转机械启动故障诊断[8-9]、电源监控[10]等应用场合，都取得了比较满意的效果。机械设备音频信号是非平稳信号，HMM是一种模拟非平稳动态模式的多元统计工具[8]。本文采集音频的特征参数矢量，用VQ算法将矢量序列转化成观察序列，用观察序列建立音频的DHMM模型进行分类识别，提出机械设备音频DHMM分析方法。

2 DHMM模型及算法

离散隐Markov模型（Discrete Hidden Markov Model，DHMM）是用来描述随机过程的统计模型。DHMM模型中有若干个状态，每个状态都有状态转移概率，表示从该状态转移到其他状态的概率。在某时刻事件必处于某一个状态，t时刻的状态只前一个时刻t-1的影响。每个状态同时还会产生一个观察值，一个状态的观察值是随机的，因此，每个状态的观察值都有相应的概率分布。

可以用参数集λ=(π，A，B)描述DHMM模型。设qt，t≥1是取值于有限状态空间ϕ={1，2，…，N}的齐次Markov链，Ot，t≥1是观察序列，取值范围为集合V={v1，v2，…，vm}。模型参数定义如下所示。

初始分布π：

状态转移概率矩阵A=(aij)：

观察值概率矩阵B=(bi(vj))：

2.1 DHMM多观察序列参数重估

DHMM需要解决的重要问题之一是给定观察序列O，如何调整模型参数λ，使概率P(O|λ)最大，这就是参数重估问题。在实现时，不仅需要通过标定方法解决前向后向变量的溢出问题，同时需要多个观察样本参与重估运算。

多观察序列的Baum-Welch的重估公式为[4-5]：

由于不同的观察序列对应的Pk=P(Ok|λ)不同，因此分子分母中的Pk不能像单个观察序列重估公式中那样消去。实际计算中的关键是对前向后向变量、进行标定及消去Pk。因为，所以

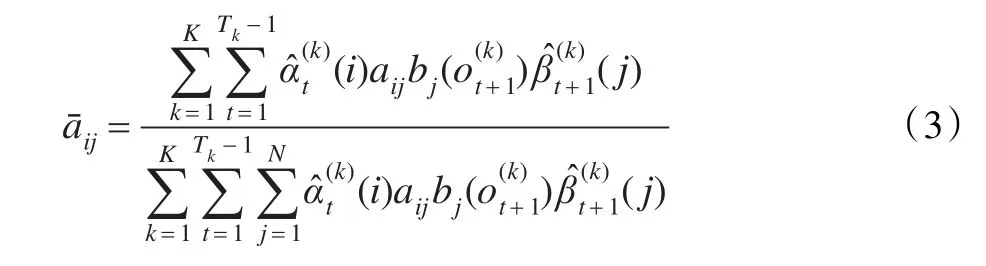
同理可得多观察序列观察值概率重估公式的标定形式为：

2.2 隐状态估计

δt(i)为沿某条路径q1，q2，…，qt，t时刻的状态qt=i且产生观察序列o1，o2，…，ot的最大概率：

可以通过归纳法计算δt(i)，递推公式为：

计算机上实现时，由于δt(i)的值很容易超出双精度浮点数的范围而出现溢出，因此实际计算δt(i)的对数值，Viterbi算法步骤如下所示。

初始化：

对（5）取对数得递推公式：

则最佳状态的概率对数值为：

而最佳状态，，…，由递推得到：

3 DHMM在机机械设备音频识别的应用

DHMM模型应用于音频识别中的结构如图1所示，系统主要由模型训练和识别过程组成。训练音频和识别音频经过采样量化后，经过滤波、预加重等预处理后再分帧，对每一帧提取特征参数。这里提取的是音频的倒谱域参数，主要有MFCC（Mel Frequency Cepstrum Coefficient）参数和 LPCC（Linear Predictive Cepstrum Coefficient）参数，都是多维矢量，分别求出了24维的MFCC参数和LPCC参数。隐马尔科夫模型的输入观察序列是标量序列，因此需要将特征参数的矢量序列转化为标量序列，矢量量化正好可以完成这样的任务。矢量量化的关键是码书设计，经典的码书设计方法是LBG算法[11]。训练码书时，先将所有不同种类的训练音频连接到一起组成一段长音频，经过预处理和特征参数提取后，通过LBG算法计算出码书。这里设计码书的大小为64，码书的码字维数是24，与特征参数的维数相同。在模型训练和音频识别过程中，分别计算训练音频和识别音频的特征参数矢量与码书中各个码字的欧式距离，取距离最小的码字的序号作为帧的观察值，这样就把输入音频转化成了观察序列，用于隐马尔科夫模型的训练和识别。

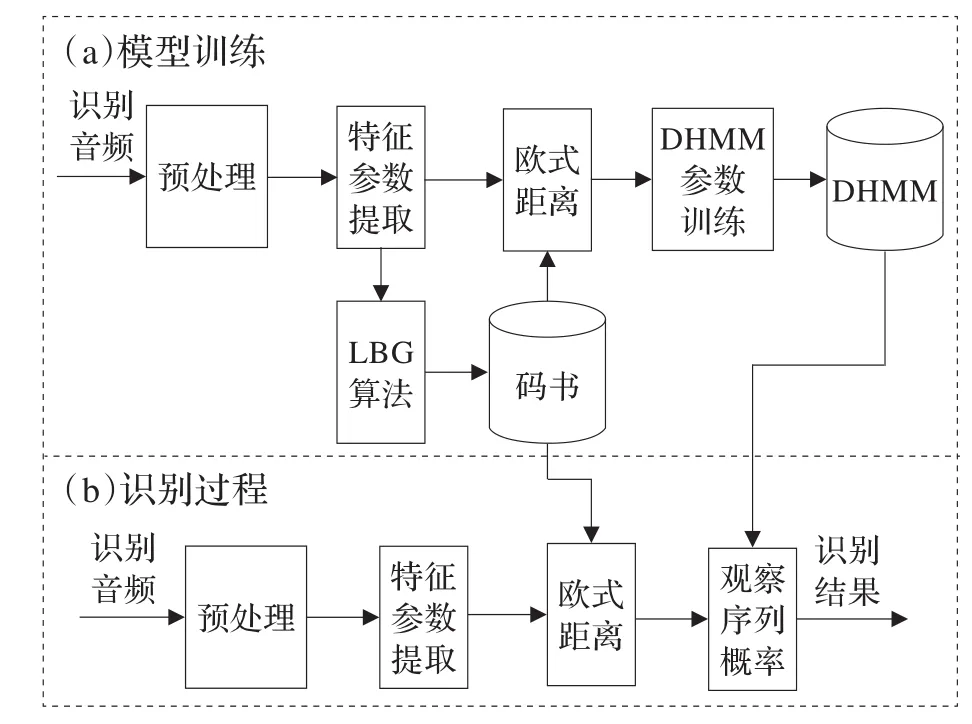
图1 音频识别系统框图

3.1 特征参数提取

MFCC参数是基于人耳听觉特性而提出的一种参数，而LPCC参数是基于音频产生模型提出的。MFCC参数提取过程如图2所示。

图2 MFCC特征参数提取图

音频首先经过预加重、分帧及加窗等处理，然后对每帧信号做快速傅里叶（FFT）变换，得到帧的短时频谱，再将频谱通过24个Mel频率三角滤波器过滤。三角滤波器不仅可以对频谱进行平滑，同时也可以滤除谐波。此处三角滤波器组在Mel频率上是均匀分布的，Mel频率和频率的关系为：

对每一个滤波器输出的能量取对数得到对数能量，用x(k)，k=1，2，…，24表示 24个滤波器输出的对数能量谱，对数能量谱进行反离散余弦变换，得到L（取L=12）个MFCC参数：

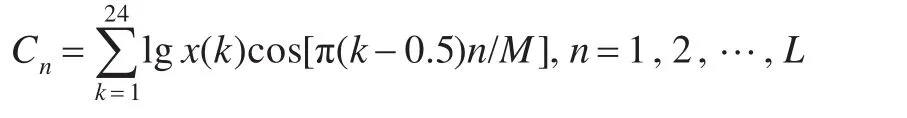
为了反映MFCC参数的动态变化情况，求MFCC参数的微分参数：

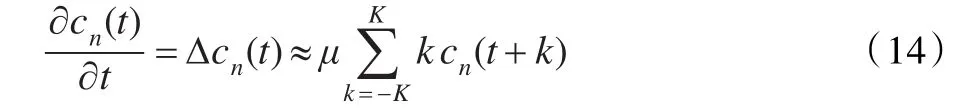
取一阶微分，得到12维的微分参数，与原MFCC参数一起构成24维的MFCC参数：

3.2 训练过程

训练DHMM时，首先将用于训练的同一种类音频分段，一般使每段音频长度为10帧到500帧。训练过程是一个迭代过程，如图3所示。由于观察值概率矩阵B的初始值对训练模型有较大影响[4]，因此需要首先估计出B的初值。相对于B，状态转移矩阵A和初始状态π的初值对训练模型的影响很小，因此A和π可根据模型的特点手动设定。估计B的初值时，先由随意设定的π、A、B初值根据Viterbi算法计算音频的隐状态，然后根据估计出的隐状态和观察值计算每个状态出现各个观察值的概率，从而得到B的初值。

图3 DHMM训练流程图

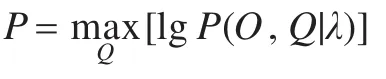
参数π决定起始状态，语音信号的字或者音素都是从发音开始作为起始状态，发音结束作为结束状态，其起始和结束状态很固定，可把发音开始状态强制定为状态1，因此它的初始概率设为：

π=(1，0，…，0)

而对于机器设备信号，起始状态与对信号分割有关，而分割是随机的，因此起始状态不确定，本文的模型的状态数为5，则它的初始状态设为等概率初始状态：

π=(0.2，0.2，0.2，0.2，0.2)

模型参数的参数A决定了DHMM的形式。语音的HMM模型一般采用图4的类型1，特点是起始状态和结束状态都固定，最后一个状态只能转移到本身。由于机械设备音频信号的起始状态和结束状态不确定，且它们的地位和其他状态是平等的，因此图4的类型2和类型3更适合于机械设备信号。类型2和类型3对应的状态转移概率矩阵初值可设为：

图4 DHMM的类型

3.3 识别过程

4 实验结果

实验分别采集了真空泵、风扇、机床、数控切割机、洗衣机、手磨机、空调、抽油烟机等机械设备不同状态共22种音频进行实验。每种音频10个样本用于训练DHMM模型，另外10个样本用于识别，HMM训练循环次数为100次。音频采样频率为8 000 Hz，经过截止频率为4 000 Hz的FIR低通滤波器后分帧，每帧长度为256个采样点，帧移为80个采样点，每一帧在处理前乘以汉明窗进行平滑。训练出的模型中真空泵阀门打开时的状态转移概率矩阵为：

图5分别是风扇3档、真空泵阀门打开、三相异步电机的波形图；图6是一段真空泵音频VQ输出的观察序列。表1给出该段音频在各个模型下的概率对数值。从表中看出，概率最大值出现在真空泵2的HMM模型下，值为-171.5，因此识别结果为真空泵2，即真空泵阀门打开音频；从表1还可以看出，第二大概率值在真空泵1的HMM下取得，值为－389.9。说明真空泵1和真空泵2音频相似，与实际情况一致，实时上，人耳很难分别两种音频。

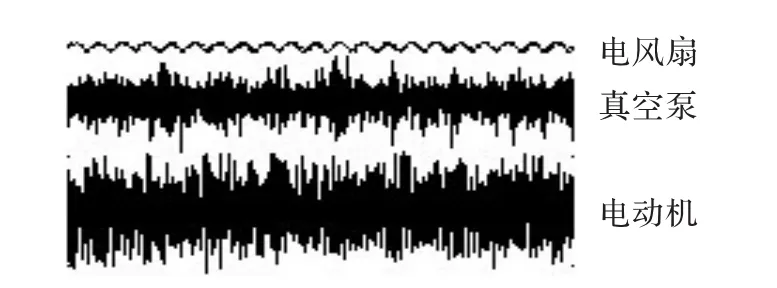
图5 三种机械音频的波形图

图6 VQ输出的真空泵阀门打开时观察值序列

表1 一段真空泵音在各HMM下的概率对数值

音频识别的实时性主要体现在识别程序的执行时间，识别程序主要的算法是Viterbi算法，由于该算法主要是随着观察序列的递归计算，所以执行时间和观察序列的长度近似成正比关系。在Windows系统下的Matlab7仿真程序中，20帧长度的音频所需的执行时间是0.1 s左右。

帧数还与识别准确率有关，因此分割时，帧数不能太大也不能太小。图7是帧数和识别准确率的关系曲线。帧数为20帧到50帧时的识别准确率较高；帧数小于4时识别准确率急剧变小，帧数增大后准确率也略有下降。

图7 音频段的帧数和识别准确率的关系

表2给出不同HMM类型采用MFCC、LPCC参数在没有噪音环境时的识别率。由表2看出，最适合机械设备音频的HMM模型为图4中的类型2，且MFCC参数比LPCC参数更适合于机械设备音频识别，识别准确率高达97%以上。另外，识别准确率与训练的HMM库的个数及VQ输出的码书大小有很大关系。当码书都为64时，将22种音频减少到10种时，识别准确率都接近100%。HMM个数越少，识别率越高；码书尺寸越大，识别率越高，但是计算量增加很多。通过实验发现在噪音环境下识别准确率有所下降，噪音对识别准确率的影响比较复杂，不同频率和能量的噪音对识别的影响不同。在噪音能量相对信号的能量小于1个数量级时，识别准确率能够满足一般需要。

表2 不同参数及不同类型HMM的识别率 （%）

5 结束语

针对机械设备音频，采用MFCC作为特征参数，应用矢量量化和隐Markov模型进行建模分析和识别，准确率可达到97%以上，可以应用于机械设备的远程监控及故障分析。对于音频特征本身相近的同种机械设备不同工作状态，识别准确率有所下降，可以采用后级方法处理。另外，需要解决噪音环境下识别问题和不同音频同时存在时的处理方法，对于未知音频，要能够给出拒绝判决标准，这些都需要进一步的研究。

[1]Baum L E.An inequality and associated maximization technique in statistical estimation for probabilistic functions of markov process[J].Inequalities，1972，3：1-8.

[2]Baum L E，Egon J A.An inequality with applications to statistical estimation for probabilistic functions of a markov process and to a model for ecology[J].Bull Amer Math Soc，1967，73：360-363.

[3]Jelinek F.Continuous speech recognition by statistical methods[J].Proc of the IEEE，1976，64（4）：532-536.

[4]Rabiner L R.A tutorial on hidden markov models and selected applications in speech recognition[J].Proc of the IEEE，1989，77（2）：257-285.

[5]Rabiner L R，Juang B H.fundamentals of speech recognition[M].New Jersey：Prentice Hall PTR，1993：321-371.

[6]肖明，贾振红.基于轮廓特征的HMM手写数字识别[J].计算机工程与应用，2010，46（33）：172-174.

[7]严焰，刘蓉，黄璐等.基于HMM的手势识别研究[J].华中师范大学学报：自然科学版，2012，46（5）：555-559.

[8]邵强，冯长建，管丽娜，等.混合密度连续HMM在旋转机械启动过程故障诊断中的应用[J].机械科学与技术，2009，28（11）：1439-1443.

[9]丁启全，冯长建，李志农，等.旋转机械启动全过程DHMM故障诊断方法研究[J].振动工程学报，2003，16（1）：41-45.

[10]程延伟，谢永成，李光升，等.基于加权HMM的车辆电源系统状态预测[J].计算机应用，2011，31（6）：1696-1698.

[11]韩纪庆，徐希利.一种基于矢量量化的音频场景分析方法[J].电声技术，2002（3）：8-10.

[12]竺乐庆，王鸿斌，张真，等.基于Mel倒谱系数和矢量量化的昆虫声音自动鉴别[J].昆虫学报，2010，53（8）：901-907.

[13]Smith W S.The scientist and engineer’s guide to digital signal processing[M].2nd ed.California：California Technical Publishing，1999：87-260.

[14]Rabiner L R，Levinson S E，Sondhi M M.On the application of vector quantization and hidden Markov models to speaker independent，isolated word recognition[J].Bell System Technical Journal，1983，62（4）：1075-1105.