南平市土地储备方案风险评估模型①

关清元，洪梦莹，陈月勤

(武夷学院数学与计算机学院，福建 武夷山354300)

0 引 言

随着城市的不断发展，土地储备方案已逐渐被提上日程.由于各方面的因素的影响，对储备方案的风险评估就显得尤其重要.本文根据所得到的南平市土地储备方案数据，用改进的灰色关联度分析的方法，结合主成分分析法，相互验证，最终得到了南平市土地储备方案总的风险评估模型.

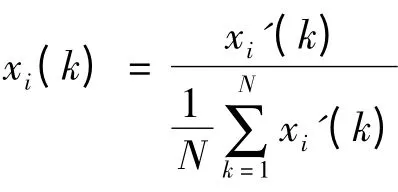
层次分析法是一种将定性与定量分析方法相结合的多目标决策分析方法，秦吉等对层次分析法的基本原理和计算方法进行了介绍［2］.

1 南平市土地储备方案的风险评估表达式确立

1.1 求灰色关联度

选取南平市区2012 年到2015 年不同区域的土地储备的地块面积，预计征收、开发资金，申请贷款额度，预期出让收益，以及回收周期作为评价指标主要因素样本，采用灰色关联分析法求各指标与总风险得分项的关联度.

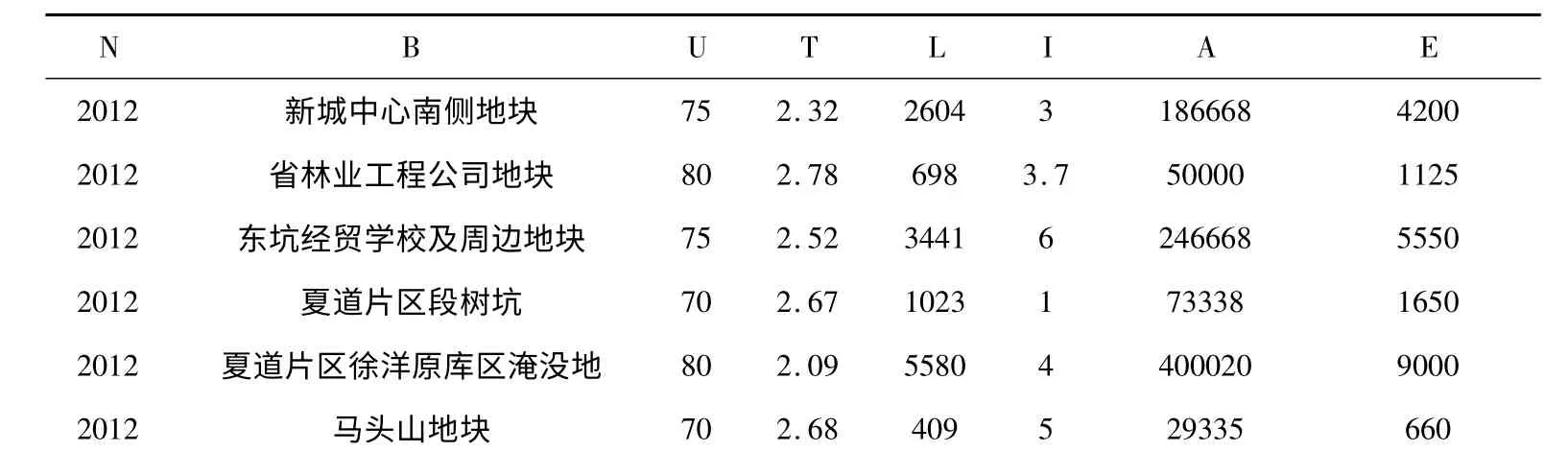
表1 各个因素的原始数据

备注:(U，T 为通过实地考察及平均估算;A，E，L，I 从为南平市人民政府对土地收购储备计划的批复中获得，有些已经换算.N 为土地储备年份(年)，B 为土地储备区域，U 为土地储备区域总风险评分，T 为平均回收周期(年)，L 为申请贷款额度(万元)，I 为预期出让收益(万元)，A 为储备地块面积(平方米)，E 为预计征收、开发资金(万元).

对表1 数据，首先对各序列进行无量纲化，采用改进的灰色关联度方法.据此可得无量纲化后的序列表2:

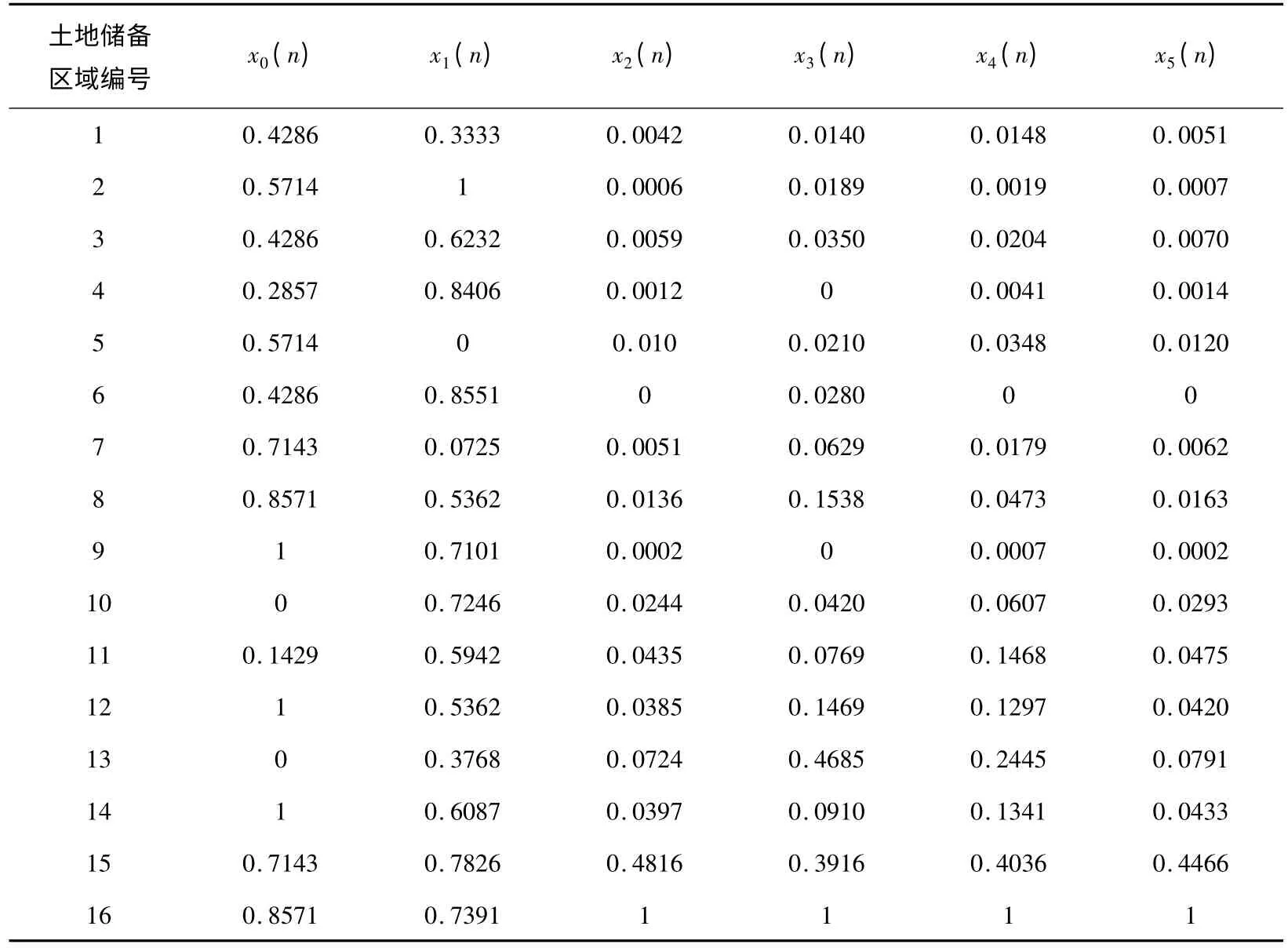
表2 无量纲化后的数据

分别计算各优选指标值与总风险评分在对应 期的间距，结果如表3 所示:

表3 对应期的间距

6 0.4265 0.4286 0.4006 0.4286 0.4286 7 0.6418 0.7092 0.6514 0.6964 0.7081 8 0.3209 0.8435 0.7033 0.8098 0.8408 9 0.2899 0.9998 1 0.9993 0.9998 10 0.7246 0.0244 0.0420 0.0607 0.0293 11 0.4513 0.0994 0.066 0.0039 0.0954 12 0.4638 0.9615 0.8531 0.8703 0.958 13 0.3768 0.0724 0.4685 0.2445 0.0791 14 0.3913 0.9603 0.909 0.8659 0.9567 15 0.0683 0.2327 0.3227 0.3107 0.2677 16 0.118 0.1429 0.1429 0.1429 0.1429

由于上述绝对值数值序列中最大的是1，最小的是0.0039，相差250 多倍，即存在着较大的数量级差异，现将其规范化:

在上表中，Δ(min)=0.0039，Δ(max)=1，此处ρ = 0.5，则 根 据(2)式 可 得 ζo1(1)=同理，可计算出其余的关联系数［4］，如表4 所示:

表4 关联系数

上述结果说明周期风险与总风险的关联度最大，储备风险次之，出让风险的关联度最小;储备风险与总风险的关联度略大于贷款风险的关联度，贷款风险与总风险的关联度略大于利率风险的关联度.

2.2 用层次分析法求权重

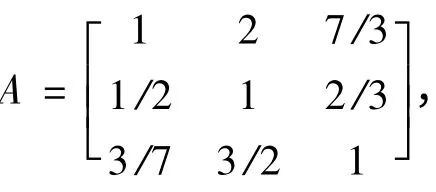
图1 用matlab 运算特征根程序

即矩阵A 的最大的特征值为λmax=3.0349

此特征根所对应的特征向量为:(0.8337，0.3459，0.4305)T，其归一化的特征向量的matlab 程序为:w1 =x(:，1)/sum(x(:，1))，可得:w(1)=(0.5178，0.2148，0.2674)T，计算矩阵A 的一致性指标为:，从而一致性比率因为CR ≺0.1，即矩阵A 的不一致程度在容许的范围之内，可用其特征向量作为权向量，同理:可得优选指标层对准则层的成对比较矩阵依次为:

BK(K=1，2，3)的一致性检验5 结果如下表:

表5 一致性检验的数据

0.1184 0.2437 0.1254 0.1223 0.0831 0.3488 0.1316 0.1247 0.2508 CIk 0.0347 0.0004 0.0071 RIk 1.12 1.12 1.12 CRk 0.0310 0.0004 0.0063

可见BK(K=1，2，3)全部通过一致性检验.

所以通过组合一致性检验.

所以可得总风险的表达式为:

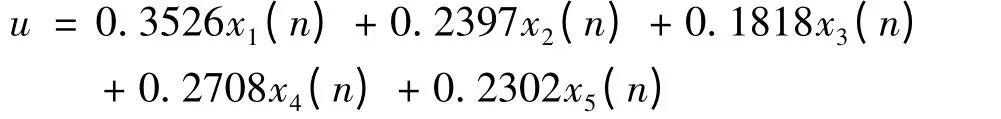
3 结 论

通过主成分分析法得到的各个因子的权重大小关系与用灰色关联因素分析所得到的关联度的大小关系是一致的，这也从一个侧面反映了主成分分析法中的各个因子的权重是合理的.从而能够更好的衡量土地储备的风险，为决策部门提供一种新的参考方法.

［1］ 李炳军，朱春阳，周杰.原始数据无量纲化处理对灰色关联序的影响［J］.河南农业大学学报，2002，36(2):199－202.

［2］ 秦吉，张翼鹏.现代统计信息分析技术在安全工程方面的应用－层次分析法原理［J］.工业安全与尘，1999，25(5):44－48.

［3］ 肖新平.灰色系统模型方法的研究［D］.华中科技大学博士论文，2002.

［4］ 吕锋，刘翔，刘泉.七种灰色系统关联度的比较研究［J］.武汉工业大学学报，2000，22(2):41－43.

［5］ 朱建军，王梦光，刘士新.AHP 判断矩阵一致性改进的若干问 题研究［J］.系统工程理论与实践，2007，27(1):18－22.