K-D 估计及其优良性研究①
杨 影,王志福,周一美,刘佳瑞,田俊杰
(渤海大学 数理学院,辽宁 锦州121013)
0 引 言
考虑线性模型[1]Y = Xβ +ε,E(ε)= 0,Cov(ε)=σ2I,设K=diag(k1,k2,k3,…,kp),D=diag(d1,d2,d3,…,dp),其中0 <di<ki<1,i=1,2,…,r,1 ≤r ≤p,称~β(K,D)= Φ1(Λ1+Kr)-1(Λ1+Dr)Φ1′^β 为K-D 估计.
设X′X 的顺序特征根为λ1,λ2,…,λp,对应的标准正交特征向量为φ1,φ2,…,φp,Φ =(φ1,φ2,…,φp)为p×p 标准正交阵Φ′Φ=I.
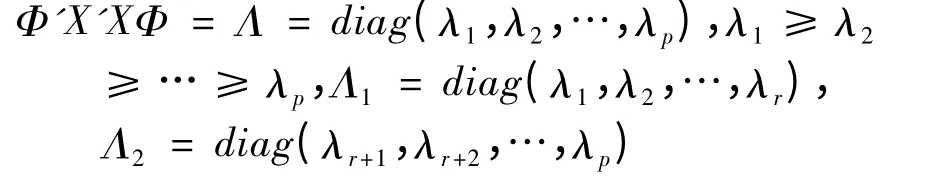
K-D 估计有如下性质:
(2)E[~β(K,D)] = Φ1(Λ1+ Kr)-1(Λ1+Dr)Φ1′β,对于r <p,且0 <di<ki<1,K-D 估计是一个有偏估计.
(2)
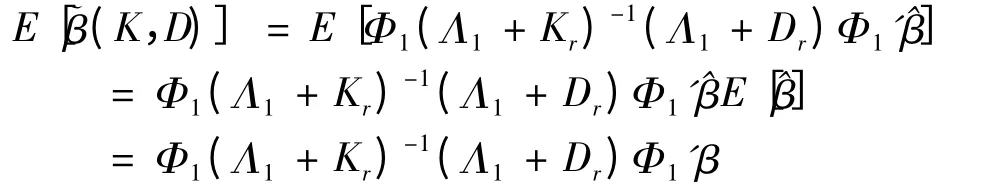
由 于,K = diag(k1,k2,k3,…,kp) D =diag(d1,d2,d3,…,dp),0 <di<ki<1,Φ1(Λ1+Kr)-1(Λ1+Dr)Φ1′β,~β(K,D)是有偏估计.
(3)
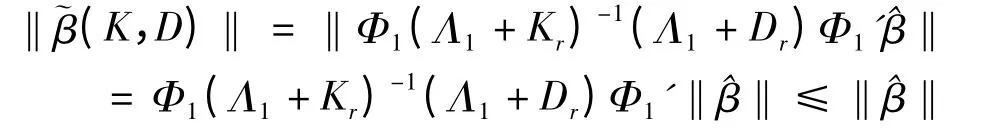
1 K-D 估计优于LS 估计
定理: 若0 <di<ki<1,则K-D 估计在均方误差矩阵意义优于LS 估计的充要条件为
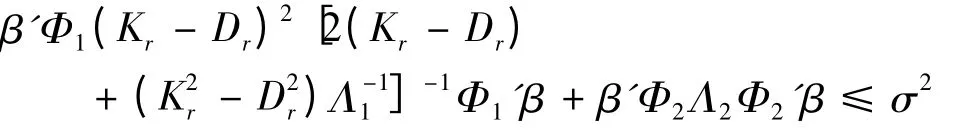
证明:LS 估计的均方误差矩阵为

则
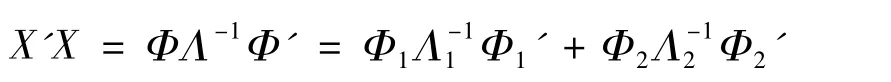
K-D 估计的均方误差矩阵为
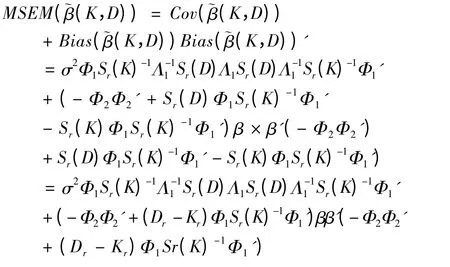
其中Sr(K)=Λ1+Kr,Sr(D)=Λ1+Dr
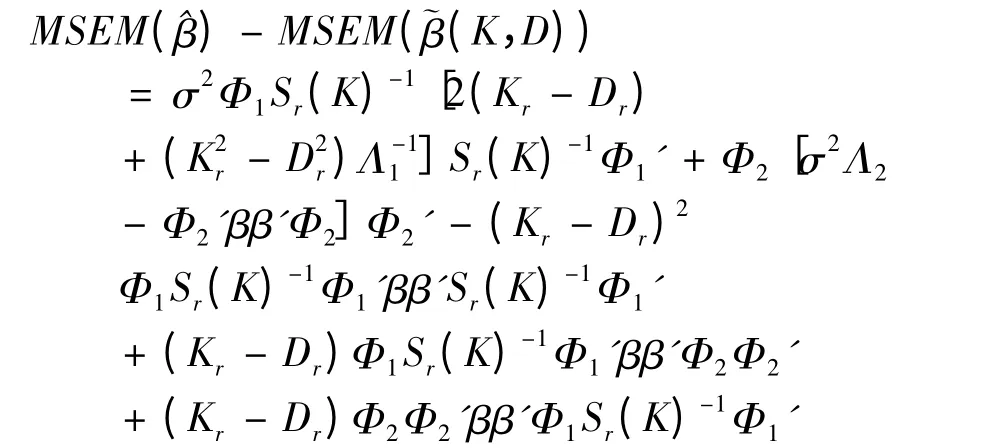
所以


2 K-D 估计的可容许性
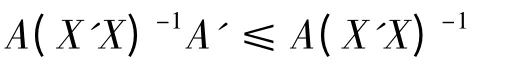
可知

则
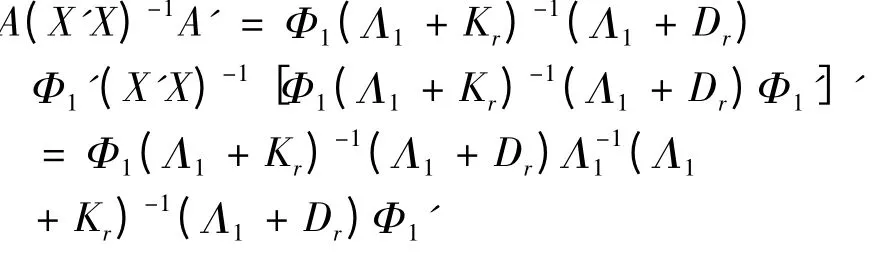

又因为λ1≥λ2≥…≥λp,则即,由于K=diag(k1,k2,k3,…,kp),D = diag(d1,d2,d3,…,dp),其中0 <di<ki<1,i=1,2,…,r,1 ≤r ≤p,称)是β 的可容许估计.
3 K-D 估计的优良性推广
对于以上证明,对估计适当变换,还可以得到K-D 估计在均方误差矩阵下优于几类常见的有偏估计的充要条件.
(1)当0 <di<ki<1,K-D 计在均方误差矩阵下优于主成分估计的充要条件为Φ1′β=0.
(2)当0 <di<ki<1,K-D 计在均方误差矩阵下优于Liu 估计的充要条件为Φ2′β=0.
[1] 陈希孺,王松桂,近代回归分析[M].合肥:安徽教育出版社,1986.
[2] 王松桂,吴密霞,贾忠贞.矩阵不等式[M].北京:科学出版社,2006.
[3] 王松桂,线性模型的理论及应用[M].合肥:安徽教育出版社,1987.
[4] 陈德英.线性模型中的LIU 型估计[D].北京:北京交通大学,2008.
[5] 邬吉波.线性模型参数估计若干性质研究[D].重庆:重庆大学2013.
[6] LIIU K.A NewClass of Biased Estimate in Linear Regression[J].Commun Stat Theory Methods,1993,22:393-402.

