基于"穷举－非线性拟合"算法下的太阳影子定位分析①

郑玉棒，张圣梅，汪 婷，张书琴，李春忠

(1.安徽财经大学统计与应用数学学院，安徽 蚌埠233030;2.安徽财经大学金融学院，安徽 蚌埠233030)

0 引 言

太阳影子定位技术就是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法.太阳的光照方向与影子的朝向相反，如果日出东北，那么影子就是朝西南，如果日落西北，那么影子就朝东南.所以影子的朝向通常被用来判断日出日落的方向，进而用来判断太阳直射点所处的半球.太阳的高度角会影响到物体影子的长度，太阳的高度角越小，影子越长，反之则影子越短.一天中太阳高度在日出和日落时都为0°，影子是最长的;而正午时太阳高度最大，此时的影子是一天中最短的.

1 数据来源与模型假设

本文数据均来自于2015 全国大学生数学建模竞赛A 题［1］.为了合理的解决问题，提出以下几点假设:(1)在较短的时间内，不考虑太阳直射点的移动;(2)太阳直射点做回归运动的移动速度是均匀的;(3)不考虑大气折射率以及所给数据的测量误差;(4)不考虑拍摄影子视频时人为带来角度差.

2 影子长度变化过程的分析模型

首先，分析得到影子长度与太阳高度角、直杆长度的关系式;其次确定太阳高度角关于参数地理纬度、太阳赤纬、时角的表达式;从而通过联立方程式得到影子长度变化的决定公式;然后利用影子长度决定公式画出2015 年10 月22 日北京时间9:00－15:00 之间天安门广场3 米高的直杆的太阳影子长度的变化曲线.

2.1 研究方法

(1)影子长度计算公式

太阳高度角即为地面太阳光线与水平地面的夹角，根据直角三角形的边角关系，可以得到直杆影子长度计算公式

其中:l 为直杆影子长度，h 为太阳高度角，d 为直杆高度.

(2)太阳高度角计算公式

太阳高度角是我们观察太阳时的仰角，随太阳赤纬、时角和地理纬度的变化而变化(太阳赤纬与地理纬度均是北纬为正，南纬为负)，由球面三角形余弦公式［3］可知

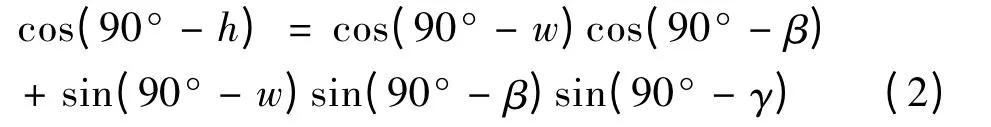
公式(2)化简即有

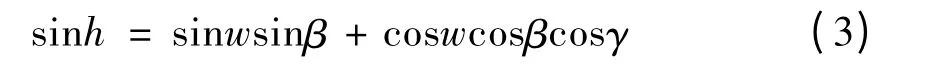
其中:w 为地理纬度，β 为太阳赤尾(太阳直射点的纬度)，γ 为时角.

1)太阳赤纬的确定

①太阳直射点的移动速度

每年太阳直射点在南北回归线之间运动度数为23°26′×4=93°44′=93.733°，一年以365 天记，得到太阳直射点运动速度为

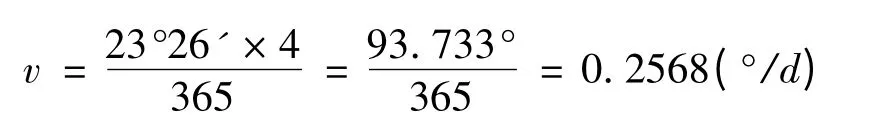
②根据日期确定太阳直射点

根据太阳直射点在南北回归线之间的运动规律，结合太阳直射点运动的速度，可以求出具体日期对应的太阳直射点所在纬度.

2)时角的确定

通过相关文献可知，当地正午12 点的时候时角是0°，前后每隔一小时增加15°，即可以得到当直杆所处地区的时间为时的时角

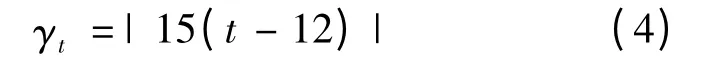
假设直杆所处地区的时间为t 时对应的北京时间为t0，直杆所处地区的经度为j.已知北京的经度是120°E，经度相隔15°E，地方时相差1 小时，且东方时间早于西方时间，即可以得出地方时与北京时间的关系为

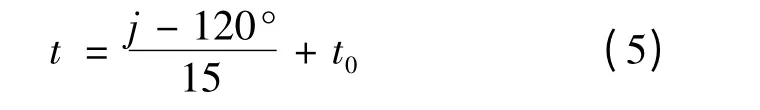
结合公式(4)可以得到直杆所处地区的时间t为时的时角γt与北京时间t0的关系

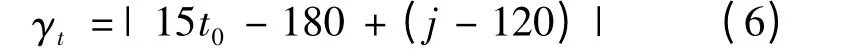
(3)影子长度变化模型

结合公式(1)，(3)，(6)，可得直杆的影子长度与直杆长度、地理纬度、地理经度、太阳赤纬和北京时间之间的关系式为公式(7)

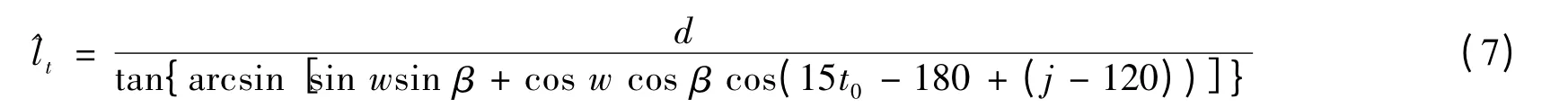
其中w 为地理纬度，j 为地理经度，β 为太阳赤尾(太阳直射点的纬度)，t0为北京时间.

公式(7)即为影子长度决定公式.

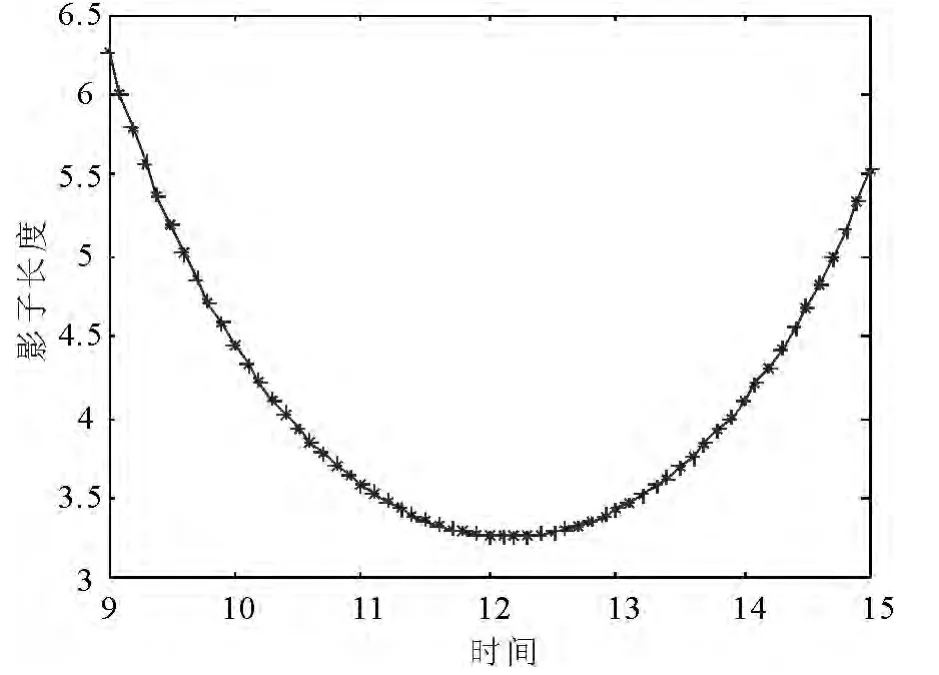
图1 直杆影子长度变化曲线

2.2 结果分析

(1)画出2015 年10 月22 日北京时间9:00－15:00 之间天安门广场，3 米高的直杆的太阳影子长度的变化曲线

1)10 月22 日太阳直射点的位置

每年秋分即9 月23 日，太阳直射点均位于赤道处，分析可知，秋分经过29 天后即为10 月22 日，随后向南回归线运动，计算可知，10 月22 日太阳直射点的位置

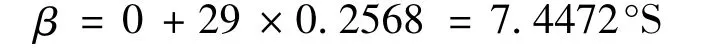
2)太阳影子长度的变化曲线

利用MATLAB 编程求解，可得直杆的影子长度变化曲线如图1 所示.

由于在北京时间为12 点16 分的时候，天安门的地方时为正午12 点，即此刻的影子最短，故有北京时间9 点的影子长度要长于北京时间15 点的影子长度，进而出现曲线不对称，即图1 所示的影子长度变化轨迹图.

(2)结果的检验

针对太阳直射点在小范围内变化时作灵敏度分析图，如图2 所示

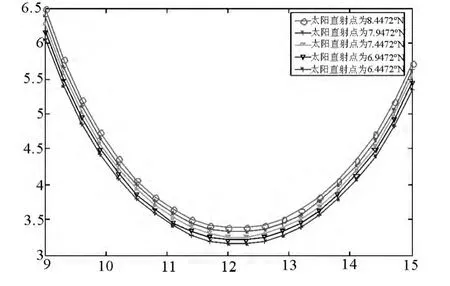
图2 灵敏度分析图

由图2 可以看出太阳直射点移动值Δβ=0.5°时，同一时刻影子长度的绝对差Δl=|l－l′|＜0.1m，由此可知对于假设1 在一天内不考虑太阳直射点的运移动导致的绝对误差ε ＜0.05136、相对误差ε ＜0.01712，由此也可说明假设(1)的合理性.

3 根据影子坐标确定直杆所处位置

3.1 研究思路

首先，根据影子坐标计算影子长度;其次，根据影子长度的变化趋势确定当地经度的范围;然后通过穷举法确定初始位置;最后利用非线性拟合，确定最佳参数，即杆最可能的位置.

3.2 研究方法

(1)计算影子长度

若t 时刻太阳影子顶点坐标为(xt，yt)，则在时刻影子长度

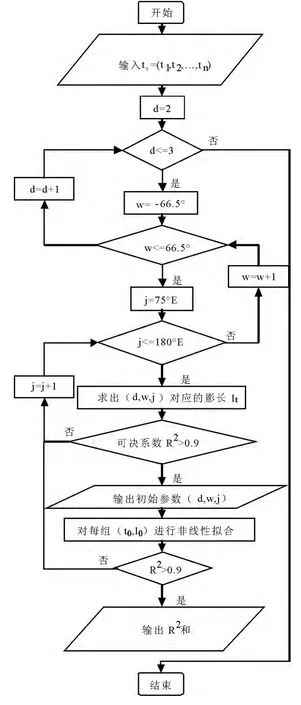
图3 "穷举－非线性拟合"算法流程图

(2)确定直杆所处位置的经度范围

由公式(5)即可以得出直杆所处位置的经度j=120°－15(t0－t)，根据影子长度变化趋势确定直杆所处位置的经度范围.结合附件1［1］的数据，得到附件1 的经度范围j ∈［79°E，180°E］.

(3)"穷举－非线性拟合"算法

1)穷举法确定初始参数

①直杆的长度d 由2m 以步长为1m 变动到3m，直杆所在的纬度w 由－66.5°以步长为1 依次变动到66.5°N(北纬为正，南纬为负)，直杆所在的经度j 由79°E 以步长为1 依次变动到180°E，三个参数相互独立变化.

②利用公式(7)，计算每一组(d，w，j)对应的影子长度③计算影子长度计算值与影子长度实际值lt之间的可决系数

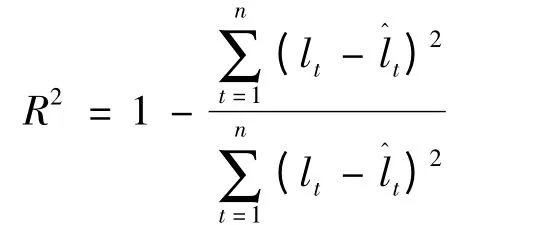
选取可决系数R2＞0.95 时所对应的(d，w，j)作为一个比较合适的初始参数值.

2)非线性拟合［2］，确定最佳参数(即直杆最可能所在的位置及直杆长度)

①根据已知数据确定参数的初始值，利用最小二乘法计算出最佳参数，使最小.

②根据可决系数R2，比较拟合效果，R2越趋近于1 表明拟合效果越好.

3)算法流程图，如图3 所示.

3.3 结果分析

根据所设计的算法，将附件1 的数据代入，利用MATLAB 编程求解，得到固定直杆的长度、固定直杆可能所处地区的经纬度值见表1.

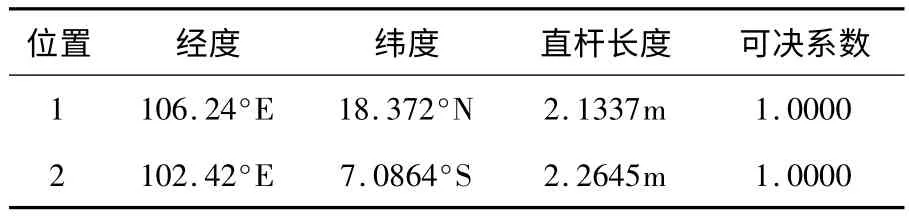
表1 附件1 中固定直杆的相关数据表

根据表1 的数据可以得出直杆所处位置大致位于18.37°N，106.24°E，或者是7.09°S，102.42°E即可得直杆所处的地理位置大致位于越南周边和印度尼西亚.

4 根据影子坐标确定直杆所处位置与测量日期

首先确定经纬度的范围;然后，在第二问的基础上，增加了参数即太阳赤尾β;最后利用"穷举－非线性拟合"算法进行求解，确定直杆最可能所在的位置、最可能测量日期.

4.1 研究方法

(1)确定各参数的范围

延续3.2 的研究方法，可以确定附件2［1］固定直杆所处位置纬度范围w ∈［－66°34′，23°26′］.固定直杆所处地经度的范围为j ∈［0°，95.1°E］.由太阳直射点的运动规律可以确定太阳赤纬β ∈［－23°26′，23°26′］.

(2)利用"穷举－非线性拟合"算法求解

1)让d，w，j，β 在取值范围内独立的取变所有整数值，根据公式(7)计算每一组(d，w，j，β)对应的影子长度

2)计算每一个(d，w，j，β)对应的影子长度计算值^lt与影子长度实际值lt之间的可决系数R2;

3)判断每一个(d，w，j，β)所对应的可决系数R2，若R2＞0.95，则此时的(d，w，j，β)为一组初始参数;

4)利用非线性拟合确定最佳参数.(即直杆最可能所在的位置、测量日期及直杆长度)

图4 图片处理过程

4.2 结果分析

结合附件2 的数据，利用MATLAB 软件编程求解得到，固定直杆的长度、固定直杆可能所处地区的经纬度、可能的测量日期等值见表2.

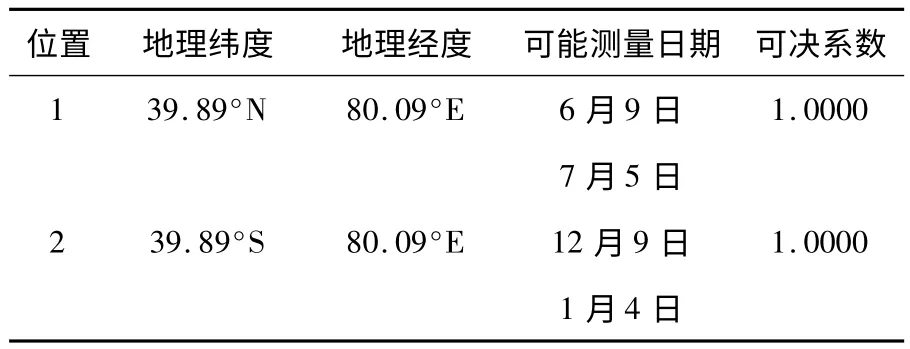
表2 附件2 中固定直杆的相关数据表

根据表2 的数据可以得出固定直杆所处位置大致位于39.89°N，80.09°E，即固定直杆所处的地理位置大致位于新疆维吾尔自治区阿克苏地区阿瓦提县，测量日期在6 月9 日或7 月5 日;由于39.89°S，80.09°E 处于印度洋，故该处舍弃.

5 根据视频确定视频拍摄地点

首先，将40 分钟的视频每隔4 分钟进行截图，并将所截取的11 张图片经过前期处理后导入到MATLAB 软件转化二值图;然后，依据像素矩阵以扫描黑色区边缘的方式得到11 组相对应得影子长度;最后利用"穷举－非线性拟合"算法确定拍摄地点.

5.1 研究方法

(1)获取固定直杆影子长度值

1)将附件4［1］中40 分钟的视频每隔4 分钟进行截图，将截取的图片预处理得到11 张含有直杆和直杆影长缩略图;

2)运用MATLAB 软件编程，将11 张含有直杆和直杆影长缩略图转化为二值图，读取像素矩阵，每张图片得到一个m×n 阶(0，1)矩阵A=(aij)其中

3)利用穷举法扫描像素矩阵，记住所有黑色像素点的行的值a=(a1，a2，…，ar)和列的值b=(b1，b2，…，bk)，令图片中杆的高度d1=max{a1，a2，…，ar}－min{a1，a2，…ar}，图片中杆的影子长度为l1=max{b1，b2，…，bk}－min{b1，b2，…，bk}，当实际杆高d=2m 时，则实际影子长度l 计算公式为

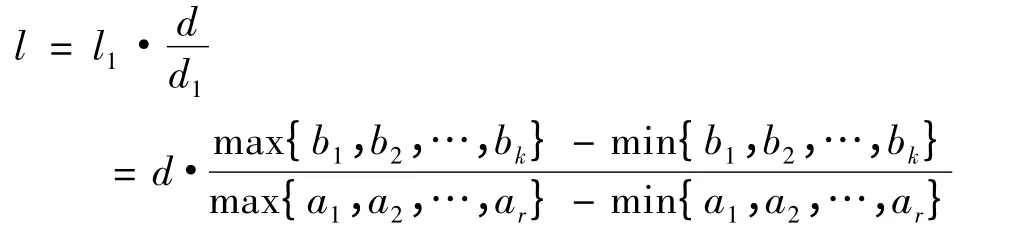
由实际影子长度计算公式可以得到从北京时间8 点54 分到北京时间9 点34 分的11 组具体影长数据如表3 所示.图4 为图片处理过程图.

表3 直杆影子长度

5.2 结果分析

由表3 中的数据，结合3 中的研究方法，利用MATLAB 软件进行求解，得到视频拍摄可能地的经纬度以及所对应的直杆长度如表4 所示.

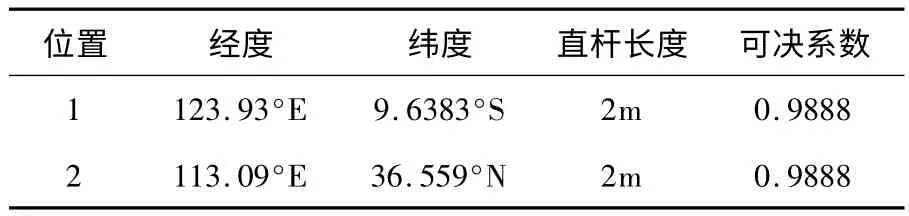
表4 最佳参数值

根据表4 的数据可以得出直杆所处位置大致位 于 123.93°E，9.64°S 或 者 是 113.09°E，36.559°N，即可得直杆所处的地理位置大致位于努沙登加拉群岛和中国山西省.

6 结束语

本文问题的解决中采取了正向思维解决逆推问题的思路，将需要求解的未知量作为参数处理，设计了通用的"穷举－非线性拟合"算法，使求解过程程序化，避免了人工求解的困扰与偶然误差.在太阳影子定位问题上提供了新的思路，用"穷举－非线性拟合"算法取代了逆推问题的常规解法.在一定程度上提高了求解的效率与准确率.

［1］ 2015 高教社杯全国大学生数学建模竞赛A 题.http://mcm.dayainfo.com/front/detailTopic.

［2］ 吴礼斌.经济数学实验与建模［M］.天津:天津大学出版社，2009.