有效转化：数学本质教学的课堂价值取向——梯形复习课的教学实录与反思

☉江苏省苏州市工业园区青剑湖学校 王小林

有效转化：数学本质教学的课堂价值取向
——梯形复习课的教学实录与反思

☉江苏省苏州市工业园区青剑湖学校 王小林

2014年4月，笔者在苏州市初二数学教学研讨活动中，开设一节初二“平面图形的认识（二）——梯形”的复习课.本文整理该课的课前准备、教学实录及教后反思，与同行研讨.

一、课前准备

1.授课对象

学生来自苏州市相城实验中学，基础较好，有一定的推理能力与研究能力，能在教师的引领下自主探究和思维建构.

2.教材分析

所用教材为《义务教育教科书数学（八年级下册）》（教育部审定2013年版），教学内容为“梯形复习”.在前面的学习中，学生已学习了解梯形的概念；理解并掌握等腰梯形的性质、识别，并能熟练运用梯形的辅助线、中位线来解决梯形的相关问题.这些内容不仅进一步发展了学生对“空间与图形”的兴趣，对学生理解、掌握、描述现实空间，获得解决实际问题的方法有着重要价值.

3.学情分析

在学习本节之前，学生已学习了三角形、平行四边形等基础知识，已经具备借助三角形、平行四边形对梯形进行处理的基础技能.通过对梯形的学习，学生对梯形、等腰梯形的概念、性质、识别有了一个较为全面的认识，对梯形与三角形、平行四边形之间的转化有了深刻的体会.当然，也有一部分学生学习这部分内容时，不是通过将梯形有效转化，而是靠简单的机械记忆去死记硬背梯形、等腰梯形的性质.基于上述的教材观、学生观、教学观，可确定下列教学目标及教学重点、难点.

4.目标要求

（1）巩固等腰三角形的性质定理，并学会综合运用；理解解决梯形问题的基本思路，转化为三角形或者平行四边形；掌握梯形问题中常见辅助线的运用.

（2）通过具体的例子，体会梯形学习中体现的从复杂到简单、从未知到已知的科学思考问题、研究问题的方法，进一步渗透转化、归纳的数学思想方法，发展合情推理和演绎推理的能力.

（3）回顾本节所学的知识与方法，对本节知识进行梳理，使所学知识系统化、结构化，进一步积累基本数学活动经验.

（4）教学重点：结构化梯形的相关知识，理解梯形问题的实质.

（5）教学难点：建构梯形知识体系，初步感受“转化”研究梯形问题.

二、教学过程简录

1.自然串发，本真梳理

师：数学思想是数学知识的灵魂，是形成数学能力、意识的桥梁.这节课老师和同学们一起来复习梯形.先请同学们对照复习目标，完成知识梳理（教师多媒体呈现，学生在学案纸上完成）.

（1）梯形的定义：一组对边平行而另一组对边_________的四边形叫梯形；或一组对边平行且不_________的四边形叫梯形；

（2）两腰_________的梯形是等腰梯形；

（3）有一个角是直角的梯形是_________；

（4）等腰梯形两腰_________；

（5）等腰梯形两腰在同一底上的_________相等；

（6）等腰梯形的两条对角线_________.

（师生一起回忆）

师：很好.在研究梯形时，谁能告诉老师解决梯形问题的方法？

生1：好像可以添加辅助线转化为三角形或平行四边形来解决.

师：很好，通过添加适当的辅助线，将梯形问题实现了转化.今天，我们将一起对梯形问题作一个系统的复习与回顾，请同学们趁热打铁完成“小试牛刀”（教师多媒体呈现，学生在学案上完成）.

①如图1，在等腰梯形ABCD中，AB=CD=8，BC=15，∠B=60°，则AD=_________.

②如图2，若梯形的上底长为4，下底长为7，一腰AD为5，则另一腰BC的取值范围为_________.

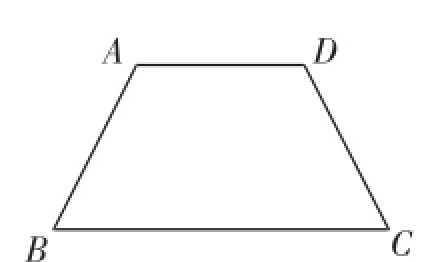
图1

图2

③如图3，梯形ABCD中，AB∥CD，∠D=70°，∠C= 40°，AB=4cm，CD=11cm，则BC=_________.

④如图4，在梯形ABCD中，AD∥BC，AB=CD，对角线相交于点O，DE∥AC交BC的延长线于点E，则△BDE是_________三角形.

图3

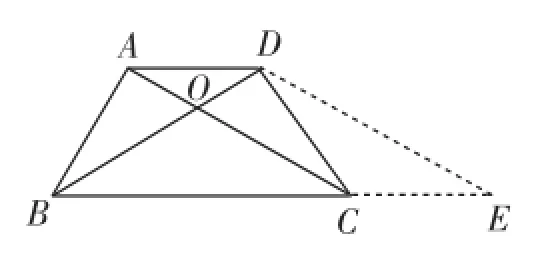
图4

生2～5讲解思路，教师追问思考过程.

师：从这些问题的解决中，我们得到什么启发？生6：通过添加辅助线，可以有效转化梯形问题.

解读：在学生“原有基础”上“自主建构”，符合学生的认知规律.正确把握知识的生长点、思维的连接点和方法的迁移点，为学生搭建好自主探究、有效转化、体验自身探索创新能力的平台.

师：今天我们将一起继续对梯形问题做深入探讨.

2.师生活动，探究性质

例1我们知道“连接三角形两边中点的线段叫做三角形的中位线”，“三角形的中位线平行于三角形的第三边，且等于第三边的一半”.类似地，我们把连接梯形两腰中点的线段叫做梯形的中位线（如图5中的EF）.试探究其有何性质？

图5

师：课前各个小组都进行了探究，下面大家把研究的成果共享一下.

生7：如图6，可以连接AF并延长交BC的延长线于点G，先利用ASA证明△ADF≌△GCF，从而得到DF=CF，则F为AG的中点，由已知E为AB的中点，从而将EF顺利地由原先的梯形ABCD的中位线转化为△ABG的中位线……

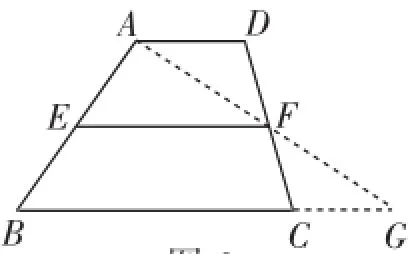
图6

师：很好！请问图6中梯形ABCD的面积与哪个图形的面积相等？

生8：因为△ADF≌△GCF，所以S梯形ABCD=S△ABG.

师：有没有其他的转化？

生9：如图7，连接BD交EF于点G，将梯形转化为△ADB和△CDB，证明EG、GF分别为△ABD、△DBC的中位线……

图7

生10：连接AC，由法2同理可得……

生11：如图8，过点A作AH∥DC交EF、BC于点G、H，证明G为AH的中点，问题也可以迎刃而解……

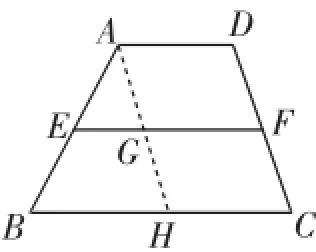
图8

师：我们来一起回顾这个问题的解决过程，无论是法1还是法2，究其本质都是通过添加辅助线，将原本梯形的中位线无一例外地转化成三角形的中位线，将未知转化为已知.

师：请同学们运用今天所学的方法，试着解决下面的问题.

例2如图9，在梯形ABCD中，AD∥BC，∠B=90°，AB=14cm，AD= 18cm，BC=21cm，点P从点A开始沿AD边向点D以1cm/s的速度移动，点Q从点C开始沿CB边向点B以2cm/s的速度移动，如果点P、Q分别从点A、C同时出发，设移动时间为t秒，当四边形PQCD是等腰梯形时，求t为多少？

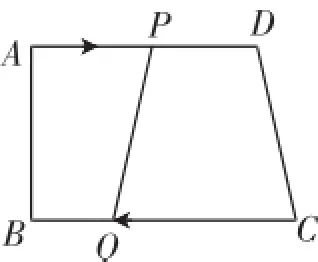
图9

师：哪一组来回答？

生12：如图10，因为AD∥BC，等腰梯形是轴对称图形，要说明四边形PQCD是等腰梯形，则作PN⊥BC，DM⊥BC，有QN=MC=3，即转化为QC-PD=6得到解决.

图10

师：这位同学回答非常好，他透过图形，看到问题实质，将所求的等腰梯形有效转化为“QC-PD=6”.

生13：如图11，由法1，可以考虑过点P作DC的平行线交QC于点E，可以直接转化为QE=6.

师：对于这个问题的处理，这两位同学都是抓住图形的几何特征，运用了转化、数形结合的思想.课后，大家考虑一下能否从代数角度利用两腰相等，通过计算解决问题？

解读：通过例1、例2的教学，引导学生在多重交互互动（师生互动、生生互动、生师互动）中体验梯形与三角形、平行四边形之间的转化，这样的探究活动发展了学生的思维能力，有效地改变了学生的学习方式，有利于掌握认识事物的一般规律；有利于学生感悟数学思想，积累数学活动经验.

图11

3.小结全课，提升理念（师生共同完成）

（1）方法比知识更重要.

（2）解决梯形问题的基本思路和方法：通过添加适当的辅助线，把梯形问题转化为平行四边形或三角形的问题来解决.

（3）梯形中常添加的辅助线有几种，由学生小结.

解读：从知识、方法、过程等方面进行课堂小结，鼓励学生从获得知识、形成技能、发展能力、养成品德等方面谈谈自己的收获及体会.不仅能帮助学生从整体上掌握所学知识和方法，而且使学生逐步体会一些重要的数学思想方法，从而提升了学生的思维含量，促进了学生的全面发展.

三、教后反思

日本著名的数学教育家米山国藏指出：“作为知识的数学出校门不到两年就忘了，唯有深深铭记于头脑中的数学精神、数学思想及研究方法等，这些随时随地发生作用，使人们终生受益.”思想方法的渗透，会使思维变得开阔、灵动.久而久之，数学的枯燥、难学就会变得趣味横生.思维的“思想”化，解题的“方法”化，是一个量变的积累过程，一个由学会向会学的转化过程.

1.精心预设，将思想方法渗透给学生

方法比知识更重要，学生在解题过程中，可能不会对自己的思维过程进行整理分析，这恰恰是教师需要引导的，要教会学生从正确的解题思路中总结方法，提高对解题的理解，最终形成学生自身的数学思维能力.在复习课的教学中，要能基于对解题这样的理解，高屋建瓴地开展教学，可以达到事半功倍的效果.在本课例中，每探究完一组题后，教师都请同学们归纳解决问题的一般方法，及时和学生分享所运用的数学思想方法，这些都充分体现了对“四基”中基本思想方法及基本活动经验的深刻理解，从而有效地提升了学生的数学素养.当然，从教学实际效果来看，把例1、例2的探究从课前移到课上，直观感受“转化思想”的生长过程，亲自体会知识从手中诞生.这不仅能提高学生学习数学的兴趣，激发学习数学的热情，而且大大拓展了数学学习的广度、深度及厚度，有利于培养学生的创新意识和再创造能力.

2.多重交互，在对话互动中共同发展

《课标（2011年版）》指出：“教学活动是师生积极参与、交往互动、共同发展的过程.有效的教学活动是学生学与老师教的统一，学生是学习的主体，教师是学习的组织者、引导者与合作者.这要求通过教师的“有效引领”，让学生“在交互中自主创新，掌握探究之法；在体验中丰富数学思想，感受数学之美”，从而实现师生的“协同发展”.可以发现，本课例中以“梯形”为主题，以转化思想的应用为主线，开门见山，以题组形式，分类呈现，在教师的“有效引导”下，“例1”、“例2”是从学生已有经验（梯形与三角形、平行四边形之间的相互转化），经历“亲自操作”、“亲自体会”、“积极参与”、“与人合作”、“自己提出并研究解决问题的方法”、“深刻体会”的过程，在体验中感悟，在感悟中升华，最后自主创新归纳得出对于梯形问题的解决策略.在这个过程中，学生获得的不仅仅是数学知识、基本技能、研究和解决问题的策略，而且体验到数学活动充满探索与创造的活力，并获得了成功的喜悦，激励了自主探究、合作学习的积极性和主动性.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.李善良.理清核心主线，优化教学过程［J］.中学数学月刊，2013（10）.

3.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.H