变权靶心贴近度在岩爆烈度预测中的应用

刘磊磊，张绍和，王晓密，郝志斌

(1.中南大学有色金属成矿预测教育部重点实验室，湖南 长沙 410083； 2.中南大学地球科学与信息物理学院，湖南 长沙 410083)



变权靶心贴近度在岩爆烈度预测中的应用

刘磊磊1,2，张绍和1,2，王晓密2，郝志斌1,2

(1.中南大学有色金属成矿预测教育部重点实验室，湖南 长沙 410083； 2.中南大学地球科学与信息物理学院，湖南 长沙 410083)

针对岩爆烈度预测的不确定性和影响岩爆发生的各单个指标间互不相容的问题，将变权理论和靶心贴近度相结合，进行岩爆烈度预测。首先，该方法在考虑评判者偏好度的基础上，引入了一种均衡函数，给出了一种变权模式，用来计算各个指标的权重；然后，该方法构造了一种区间关联函数，将单指标关联函数的最大值作为靶心坐标，根据样本与靶心的贴近度来预测岩爆烈度，即靶心贴近度值越大，则岩爆烈度越接近该贴近度所对应的岩爆烈度等级；最后，将该方法应用于灵宝东峪矿区、冬瓜山铜矿和秦岭隧道岩爆预测等实例中，结果表明：该方法不仅可以准确、合理地预测岩爆烈度，而且相比其他方法，该方法不需要任何先验知识，使用起来更直接、更方便。

爆炸力学；靶心贴近度；层次分析法；烈度预测；岩爆；关联函数；变权

岩爆是在高地应力地区地下工程开挖过程中比较常见的一种动力地质灾害现象，由于在发生过程中常常伴随着巨大的能量释放且其孕育过程缓慢不易察觉，因而极具灾难性和突发性，容易造成设备损坏和人员伤亡,不仅影响工期，而且对工程造成不可估量的损失。岩爆预测能够对实际工程的设计和施工起指导作用，为岩爆防治提供时间、地点以及危险程度等信息。岩爆发生机理是有效预测岩爆的理论基础。

自18世纪40年代以来，在岩爆的理论研究方面成果颇丰，提出了强度理论、能量理论、失稳理论、损失理论、岩爆倾向理论、微观破裂机制理论、分形理论以及突变理论等，可谓百家争鸣。但是，各个理论的出发点和考虑的因素各不相同或者比较单一，导致对岩爆的作用机理至今未形成统一的定论，岩爆问题已经成为一个世界难题。

近年来，在岩爆预测方面也有了一些新的进展，各种预测理论在其相应的适用条件下也取得了良好的效果，如：高玮等[1]基于工程类比的思想将改进的蚁群聚类算法应用于岩爆预测；刘晓辉等[2]提出了岩爆预测的微震监测法；张志龙等[3]运用地质综合分析法和Russense判据法成功预测了雪峰山隧道岩爆；罗磊等[4]建立了岩爆烈度预测的加权距离判别模型；冯夏庭等[5]研究了岩爆孕育的时空变化规律，对深埋隧道的岩爆预测和动态调控提供了重要的基础。

总的来说，以上方法不外乎分为理论判据法、现场实测法和工程类比法。然而，理论法限于岩爆机理的复杂不确定性往往比较单一，现场实测法一般滞后实际岩爆发生状况，使得预测结果有一定的偏差。同时，工程类比法虽能较综合地预测岩爆发生，但大多忽略了岩爆各因素的影响不同或者不能准确评价各因素的影响程度，如加权距离判别法也只是从常权评价的角度考虑了各因素的影响重要性，而并没有考虑到各因素重要性随岩爆状态而变化的情况。基于此，本文中在综合考虑岩爆各个影响因素的基础上，将变权靶心贴近度的方法引入岩爆预测中，以期能够取得较好的效果，为岩爆烈度预测提供一种新的思路和方法。

1 岩爆主要影响因素及烈度评价标准

1.1 岩爆发生与岩性有关

工程实践表明，发生岩爆的岩石新鲜完整、质地坚硬或者基本没有裂隙存在。一般情况下，当岩石的单轴抗压强度达到一定数值后，岩质越坚硬，岩体越易存储能量，岩爆越易发生。陆家佑[6]考虑到与岩爆发生有关的岩石单轴抗压强度的影响，提出了以下判别准则：

(1)

式中：σθ为洞室围岩切向应力；Rc为岩石单轴抗压强度；Ks取值与岩石的单轴抗拉强度和单轴抗压强度比Rt/Rc有关，且当Rt/Rc取值分别为0.25、0.5、0.75和1.0时，Ks依次为0.3、0.4、0.45和0.5，中间值可采用插值法求得。

1.2 岩爆发生与地应力有关

岩爆的发生与地应力的量级有着密切的关系，因此，岩爆发生地区地应力一般都较高。通常情况下，高地应力地区，岩石所具有的弹性模量越高，岩石越易聚集弹性能量，在岩体开挖过程中也容易形成破碎区，导致岩爆易发生。这是因为，在开挖卸荷过程中，改变了岩体赋存的空间环境，破坏了围岩的初始地应力，打破了洞室围岩的平衡状态，引起周围岩体应力重分布，导致局部地方应力集中，当应力聚集到一定程度达到岩爆临界应力时产生岩爆[7]。学者们以地应力为基础建立了许多相关的岩爆应力判据，而且在实际中也取得了良好的效果，如Russenes判别法、Turchaninov判别法、Hook岩爆判别法、Barton判别法、陶振宇判别准则、徐林生二郎山公路隧道判别法等。

1.3 岩爆发生与能量有关

A.Kidybinski[8]根据对煤的实验提出了弹性应变能指数判据，即岩爆和弹性应变能与损耗应变能之比有关；赵本钓[9]通过岩石变形曲线将岩爆与峰值前岩石的变形能的积累和峰值后岩石破坏所需的能量密切联系起来，提出了岩爆的冲击能量指数指标；在A.Kidybinski和赵本钓的基础上，唐礼忠等[10]通过分析岩石破坏过程中的能量变化，提出以岩石在峰值强度前储存的弹性应变能和峰值强度后稳定破坏所需的能量耗散之差(即剩余能量)与峰值强度后稳定破坏所需的能量耗散之比作为剩余能量指数，以反映岩石在峰值强度后区的动态特性，结果表明该指标能够较好地反映岩石的岩爆倾向。因此，岩爆的发生与能量有着密切的联系。

1.4 岩爆烈度评价标准

根据上述对岩爆主要影响因素的分析，考虑岩爆发生的内外条件，王元汉等[11]建立了一种岩爆烈度与各影响因子之间的综合指标评价标准(表1)，将岩爆烈度分为4个等级：无岩爆(Ⅰ级)、轻微岩爆(Ⅱ级)、中等岩爆(Ⅲ级)和强岩爆(Ⅳ级)。表中：σθ/σc为围岩最大切向应力与岩石单轴抗压强度比，σc/σt为岩石单轴抗压强度与岩石单轴抗拉强度比，wet为弹性能量指数。

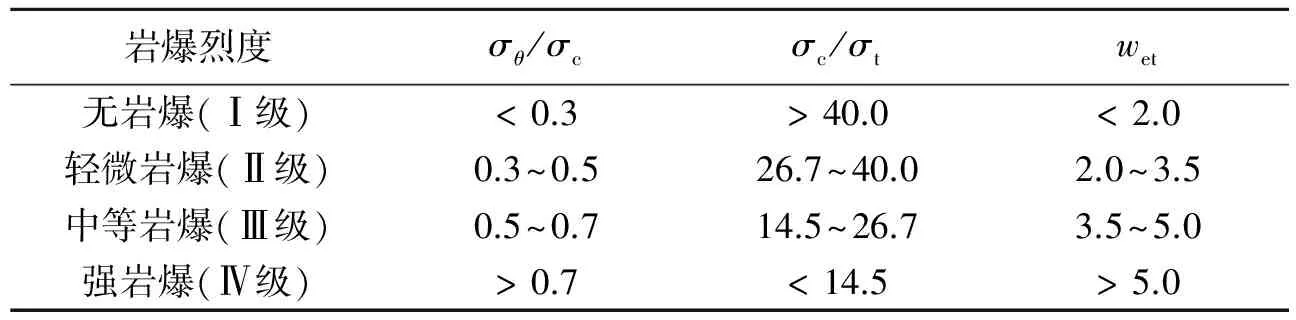
表1 岩爆烈度与各主控因子之间的关系

2 变权靶心贴近度法

2.1 区间关联函数

设有m个样本，每个样本包含n个评价指标，记第i个样本在第j个指标下的属性值为xij。根据一定的规律或者法则，可以将所有样本分成p个评价类(如上述岩爆烈度可以分为4个等级)，则在第j个指标的取值区间内插入p-1个分点，将其分为以下p个子区间：[aj0，aj1]，…，[ajk-1，ajk]，…，[ajp-1，ajp]。则第i个对象在第j个指标下关于第k个评价类(区间)[ajk-1，ajk]的关联函数为：

(2)

关联函数值越大，说明属性值越接近分类区间的中点。当μijk>0时，表示属性值在分类区间内；当μijk<0时，表示属性值在分类区间外；当μijk=0时，表示属性值在分类区间临界值上[12]。

2.2 靶心贴近度

根据文献[12]，将上述单个指标对各区间关联函数值的最大值作为评价对象的靶心坐标，表示为：

(3)

式中：μij表示单指标关联函数的最大值；i∈[1,m]，j∈[1,n],k∈[1,p]。则第i个样本的靶心可以表示为：(μi1，μi2，…，μin)。因此，设第i个评价样本关于第k个评价类的靶心贴近度为：

(4)

式中：wij表示第i个评价样本关于第j个指标的权重。

2.3 变权的层次分析法求权重

2.3.1 层次分析法

层次分析法(AHP)[13]是将研究对象分为不同的因素，并按照各因素之间的关系将各因素组合成不同的层次，确定各因素之间的相对重要性，在实际中能有效解决难以定性或定量解决的复杂问题。其主要求解步骤如下：

(1)构建判断矩阵。层次分析法需要以相应的信息作为基础，而信息来源于人们对不同层次各个因素之间的相对重要性所作出的判断，为了将这种判断量化，引入了适当的判断标度，将判断以数字的形式体现，从而构成判断矩阵，标度方法见表2，其中bij表示因子i与j进行比较所得到的标度值，且满足bij=1/bij。

表2 标度意义表

(2)一致性检验。根据以上判断矩阵求出其最大特征值λmax对应的特征向量，并作归一化处理，得到新的向量W，该向量中的每个元素值对应着相应因子的权重。一致性判断标准用指标C表示，当C=0.1时，一致性较好，较合理；当C<0.1时，一致性很好，很合理；当C>0.1时，一致性差，不合理，判断不合理则需要重新调整元素取值。其计算公式为:

(5)

(6)

式中：Ci表示一致性指标，Ri表示平均随机一致性指标，其取值标准按表3选择，n表示因子的个数。

表3 平均随机一致性指标

2.3.2 均衡函数与变权模式

传统的层次分析法在满足一致性检验的基础上，虽能体现各因素之间的不同重要性，但是往往具有过度的主观色彩。另外，层次分析法所得权重体系一般固定不变，而不会随着样本或者对象的变化而变化，因而不能反映复杂样本的系统非线性等特征。考虑到这些缺陷，本文中建立了一种均衡函数，通过获取样本中的信息，对层次分析法求得的权重进行自动调整，用已体现出决策者在对象评价过程中的偏好，最后得出一种变权模式。

设层次分析法所求得的指标权重为：

采用文献[14]中提供的均衡函数

则可以得到的变权公式为：

(7)

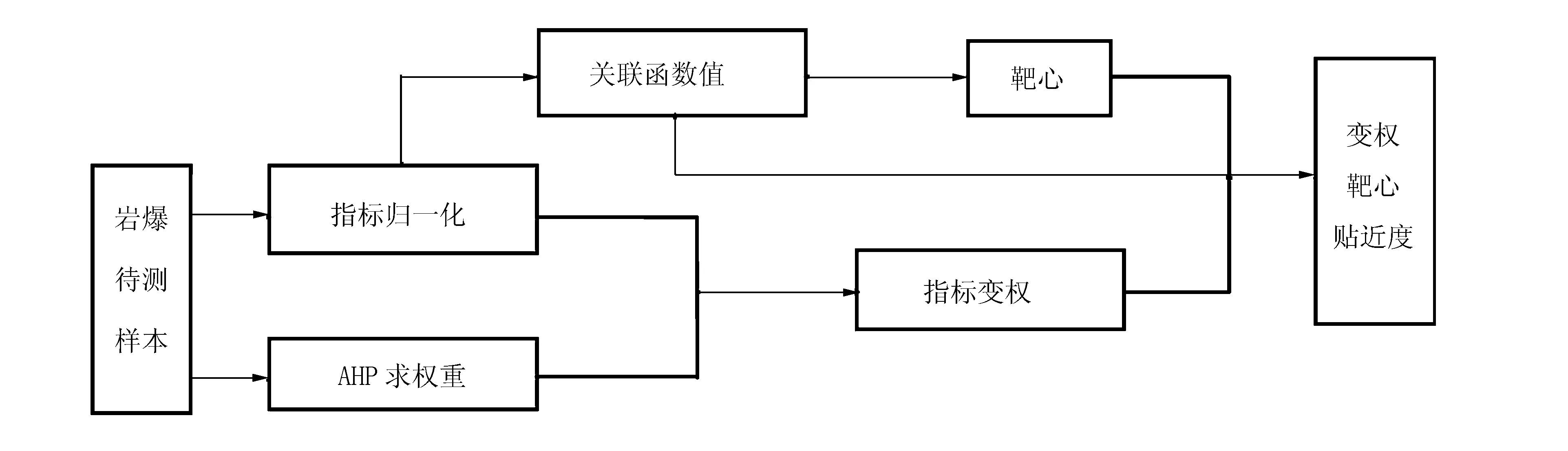
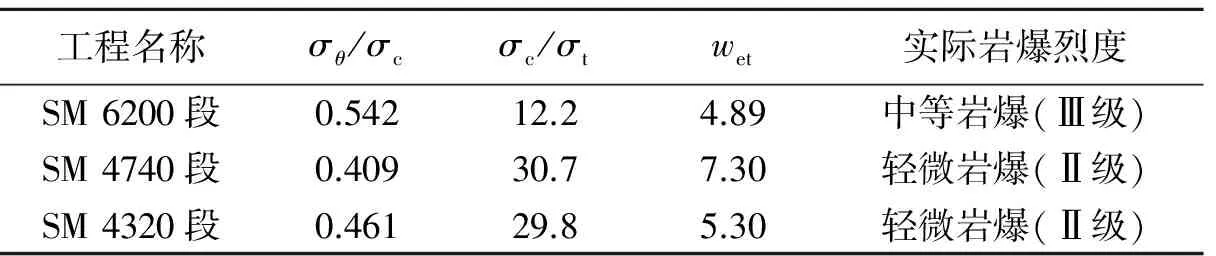
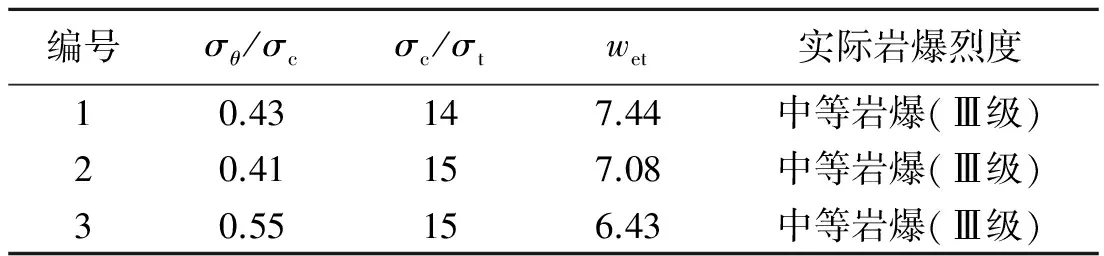
式中：a为参数。当评价者过于保守，对各指标的均衡问题考虑较多时，0

3 工程应用

3.1 岩爆烈度预测的变权靶心贴近度法计算流程

依据上述变权靶心贴近度法的基本原理，将其应用于岩爆烈度预测，其模型计算流程如图1所示。

图1 计算流程图Fig.1 Calculation flow chart

3.2 工程实例1

灵宝东峪矿区概况[15]：矿区888坑口巷道长9 km，穿越5条含金矿脉，矿体围岩主要为条带状混合岩和黑云斜长片麻岩，多呈块状结构，岩体稳固性好，同时，矿区于888坑SM6200附近设置了一个用于探矿和运输的38#竖井，竖井设计高度600 m，工程穿越混合花岗岩和片麻岩，施工过程中出现了岩爆现象。由文献[15]可知，矿区岩体力学性质参数及实际岩爆烈度见表4。根据上述变权贴近度方法的基本介绍，采用层次分析法求得3个指标的权重依次为：0.5、0.25、0.25，且满足一致性检验要求。然后，依据靶心公式和变权的方法，可以分别求出3个样本的变权模式和靶心坐标，见表5。最后，根据公式(2)～(4)即可得出各个待测工程段在岩爆各等级下的贴近度，见表6。

表4 灵宝东峪矿区岩爆参数

表5 灵宝东峪矿区岩爆参数变权及靶心

表6 灵宝东峪矿区岩爆烈度预测结果

由表6可知：矿区内将有轻微～中等岩爆发生。由文献[15]可知，实际施工过程中，竖井和天轮洞室及永久卷扬洞室等在开挖下掘时发生过中等规模的岩爆现象，与此同时，SM 4740段和SM 4320段也曾发生过轻微岩爆现象。因此，本文方法预测结果与实际情况基本一致，表明本文方法具有一定的实用性。同时将本文方法也与Bayes方法所得的结果相比较，结果也吻合，但是Bayes法需要依据大量的训练稳定的样本才能判断，而该方法则不需要依赖于样本，可以直接用来判别，因而是有效的。

3.2 工程实例2

铜陵有色金属(集团)冬瓜山铜矿是我国首家有岩爆倾向的典型深埋硬岩金属矿山，在其开采过程中可能发生岩爆，就其岩爆倾向的控制，国家科委“九五“期间对此立项展开了相关研究，岩爆参数如表7所示[15]。根据变权靶心贴近度的基本原理，由公式(2)～(7)可以得出待测岩爆实例的变权和靶心、以及靶心贴近度，分别见表8和表9。

表7 冬瓜山矿区岩爆参数

表8 冬瓜山矿区岩爆参数变权及靶心

表9 冬瓜山矿区岩爆烈度预测结果

表9结果表明：采用该方法预测冬瓜山铜矿矿区矽卡岩中将可能产生中等烈度的岩爆，这与实际情况在-790 m处矽卡岩中出现的岩爆情况一致，进一步说明了本文方法的合理性。同时，将本文结果与Bayes判别方法预测结果进行比较，也基本吻合，但是使用该方法不需要依赖样本，使用更方便、更直接，侧面说明了本文方法的有效性。

3.4 工程实例3

西康秦岭隧道工程概况：隧道长约18.46 km，由2条间距30 m相互平行的单线隧道组成，是我国最长的铁路隧道，最大埋深约为1 600 m，由于隧道所遇低层为混合岩层，且岩性坚硬，为脆性岩体，是岩爆易发地带，实际过程中所测得的岩爆数据见表10。根据变权靶心贴近度的基本原理，由公式(2)～(7)可以得出待测岩爆实例的变权和靶心、以及靶心贴近度，分别见表11和表12。

表10 秦岭隧道岩爆实测数据[16]

表11 秦岭隧道岩爆参数变权及靶心

表12 秦岭隧道岩爆烈度预测结果

表12的结果表明：采用该方法对秦岭隧道2处岩爆进行预测，判别结果较准确。对于1#岩爆实例，本文方法判断结果偏保守，分析原因主要是文中关联函数和均衡函数的选取精度不够或者匹配不是最佳，导致数据传递过程中会有部分的损失，但是总的来讲，该方法对于实际指导设计和施工是偏于安全的。最后，将本文方法与文献[7]中距离判别法相比较，结果较一致，但是该方法的优势在于不需要依赖已有样本的信息，对样本没有要求，判别过程比较直观。

4 结 论

(1)针对岩爆烈度评价单指标间互不相容的问题，构建一种新的关联函数，以单指标关联函数的最大值作为岩爆样本的靶心坐标，根据样本与靶心之间的贴近度，对岩爆烈度进行预测，计算方便，且效果较好。

(2)岩爆各影响因素之间的重要性不同，以往各指标权重所采用的是常权模式，没有考虑到因不同地区样本信息不同所引起的权重变化，对此，提出了一种考虑评判者均衡度的变权模式。

(3)将变权靶心贴近度法引入实际工程中，可以准确、合理地解决岩爆烈度预测的问题，与Bayes判别法及其他需要依赖训练样本的方法相比较，使用该方法更方便、更直接，为岩爆烈度预测提供了一种有效的途径。

[1] 高玮,张飞君.深部地下工程岩爆预测的筛选蚁群聚类算法[J].爆炸与冲击,2012,32(6):568-572. Gao Wei, Zhang Fei-jun. Forecasting of rockburst in deep underground engineering based on abstraction ant colony clustering algorithm[J]. Explosion and Shock Waves, 2012,32(6):568-572.

[2] 刘晓辉,吴爱祥,王春来,等.某深井矿山岩爆预测模式研究[J].采矿与安全工程学报,2012,29(1):78-83. Liu Xiao-hui, Wu Ai-xiang, Wang Chun-lai, et al. Study on rockburst forecasting prediction in a deep mine[J]. Journal of Mining & Safety Engineering, 2012,29(1):78-83.

[3] 张志龙,李天斌,王兰生,等.雪峰山隧道岩爆问题预测研究[J].煤田地质与勘探,2005,33(1):58-60. Zhang Zhi-long, Li Tian-bin, Wang Lang-sheng, et al. Predictive of rockburst in the Xuefeng mountain express highway tunnel[J]. Coal Geology & Exploration, 2005,33(1):58-60.

[4] 罗磊,曹平.深部巷道岩爆加权距离判别法模型的分析和应用[J].中南大学学报:自然科学版,2012,43(10):3971-3975. Luo Lei, Cao Ping. Model of weighted distance discriminant analysis and application for deep roadway[J]. Journal of Central South University: Science and Technology, 2012,43(10):3971-3975.

[5] 冯夏庭,陈炳瑞,明华军,等.深部隧洞岩爆孕育规律与机制：即时型岩爆[J].岩石力学与工程学报,2012,31(3):433-444. Feng Xia-ting, Chen Bing-rui, Ming Hua-jun, et al. Evolution law and mechanism of rockbursts in deep tunnels: Immediate rockburst[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(3):433-444.

[6] 宫凤强,李夕兵.岩爆发生和烈度分级预测的距离判别方法及应用[J].岩石力学与工程学报,2007,26(5):1012-1018. Gong Feng-qiang, Li Xi-bing. A distance distancenant analysis method for prediction of possibility and classification of rockburst and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(5):1012-1018.

[7] 孙旭宁,赵国斌,张国泉.岩爆的影响因素分析与预测[J].施工技术,2012,41(367):60-63. Sun Xu-ning, Zhao Guo-bin, Zhang Guo-quan. Analysis of influencing factors and prediction on rockburst[J]. Construction Technology, 2012,41(367):60-63.

[8] Kidybinski A. Bursting liability indices of coal[J]. International Journal of Rock Mechanics and Mining Sciences， 1981，18(6):295-304.

[9] 赵本钓.冲击地压及其防治[M].北京：煤炭工业出版社，1995:241-245.

[10] 唐礼忠,潘长良,王文星.用于分析岩爆倾向性的剩余能量指数[J].中南工业大学学报,2002,33(2):129-132. Tang Li-zhong, Pan Chang-liang, Wang Wen-xing. Surplus energy index for analysing rock burst proneness[J]. Journal of Central South University of Technology, 2002,33(2):129-132.

[11] 王元汉,李卧东,李启光,等.岩爆预测的模糊数学综合评判方法[J].岩石力学与工程学报,1998,17(5):493-501. Wang Yuan-han, Li Wo-dong, Li Qi-guang, et al. Method of fuzzy comprehensive evaluations for rockburst prediction[J]. Chinese Journal of Rock Mechanics and Engineering, 1998,17(5):493-501.

[12] 夏连学,张慧颖.变权靶心贴近度在膨胀土分类中的应用[J].长安大学学报:自然科学版,2008,28(4):32-34. Xia Lian-xue, Zhang Hui-ying. Application of target approaching in variable weight to expansive soil classification[J]. Journal of Chang’an University: Natural Science Edition, 2008,28(4):32-34.

[13] 张勇慧,李红旭,盛谦,等.基于模糊综合评判的公路岩质边坡稳定性分级研究[J].岩土力学,2010,31(10):3151-3156. Zhang Yong-hui, Li Hong-xu, Sheng Qian, et al. Study of stability gradation of highway rock slopes based on fuzzy comprehensive evaluation[J]. Rock and Soil Mechanics, 2010,31(10):3151-3156.

[14] 刘文奇.均衡函数及其在变权综合中的应用[J].系统工程理论与实践,1997,17(4):58-64. Liu Wen-qi. Balanced function and its application for variable weight synthesizing[J]. Systems Engineering-Theory & Practice, 1997,17(4):58-64.

[15] 付玉华,董陇军.岩爆预测的Bayes判别模型及应用[J].中国矿业大学学报,2009,38(4):528-533. Fu Yu-hua, Dong Long-jun. Bayes discriminant analysis model and its application to the prediction and classification of rockburst[J]. Journal of China University of Mining & Technology, 2009,38(4):528-533.

[16] 白明洲,王连俊,许兆义.岩爆危险性预测的神经网络模型及应用研究[J].中国安全科学学报,2002,12(4):65-69. Bai Ming-zhou, Wang Lian-jun, Xu Zhao-yi. Study on a neutral network model and its application to predict the risk of rock blast[J]. China Safety Science Journal, 2002,12(4):65-69.

(责任编辑 曾月蓉)

Application of target approaching with variable weight in prediction of rockburst intensity

Liu Lei-lei1,2, Zhang Shao-he1,2, Wang Xiao-mi2, Hao Zhi-bin1,2

(1.KeyLaboratoryofMetallogenicPredictionofNonferrousMetalsMinistryofEducation,CentralSouthUniversity,Changsha410083,Hunan,China； 2.SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,Hunan,China)

According to the uncertainty of rock burst intensity prediction and the incompatible problem of the single index which mainly influences the rock burst， a method combining variable weight theory with the degree of target approaching is proposed to make prediction of rock burst intensity. First, considering the preference degree of the judge, a variable weight model is given to calculate the weights of indexes based on a balance function. Second, this method constructs an interval incidence function, and the maximum value of incidence function for single index is used to be the target, so the rock burst intensity can be predicted based on the degree of approaching between samples and targets-the larger degree of the target approaching, the higher intensity of the rock burst. Finally, this method is applied to Dongyu rock mine in Lingbao, Dongguashan rock mine and Qinling Tunnel rock burst, and the results show that it can predict the rock burst intensity correctly and reasonably. What’s more, compared with other methods like Bayes discriminant analysis method and distance discriminant analysis method(DDA), it doesn’t need any prior knowledge, and so is very direct and convenient for calculation. Therefore, this method is worthy of promotion and application.

mechanics of explosion; target approaching； AHP； prediction of intensity； rockburst； incidence function； variable weight

10.11883/1001-1455(2015)01-0043-08

2013-05-03；

2013-07-31

国家自然科学基金项目(51074180)

刘磊磊(1987— )，男，硕士研究生;通讯作者： 张绍和，452041789@qq.com。

O382；TU457 国标学科代码： 13035

A