非嵌入式多项式混沌法在爆轰产物JWL参数评估中的应用

王瑞利,刘 全,温万治

(北京应用物理与计算数学研究所，北京 100094)



非嵌入式多项式混沌法在爆轰产物JWL参数评估中的应用

王瑞利,刘 全,温万治

(北京应用物理与计算数学研究所，北京 100094)

介绍了非嵌入多项式混沌法的数学模型，给出了非嵌入式多项式混沌法进行不确定度量化的主要步骤。采用此方法研究了平面、散心爆轰问题数值模拟中,JWL模型参数R1、R2服从均匀分布的随机变量时所引起的爆轰过程计算结果的不确度性，着重分析了爆轰传播过程中压力与密度的统计特性。研究结果表明，非嵌入式多项式混沌法可以为模型输入参数不确定性的传播对输出结果响应量的影响建立一种有效不确定度评估方法，为使用JWL模型时选取参数提供参考。

爆炸力学；JWL状态方程；参数选取;非嵌入式多项式混沌法；不确定度量化

炸药的点火、爆轰传播研究是炸药装置设计以及安全性、可靠性研究中的重要问题。炸药爆轰产物状态方程是描述炸药爆轰CJ状态之后的爆轰产物系统各物理量之间的关系式。目前，已有多种爆轰产物状态方程形式，如等熵γ律状态方程、BKW及JWL状态方程[1]等。JWL(Jones-Wilkins-Lee)状态方程的形式为：

(1)

式中：P为爆轰产物的压力，v为爆轰产物的相对比容，A、B、R1、R2和w是5个待定参数。合理确定这些参数值，才能比较精确地描述爆轰产物的膨胀驱动做功过程。开展输入参数不确定度对输出结果不确定度传播与量化的研究是合理选取参数的重要保证。传统用于不确定度量化的方法有蒙特卡洛法、微扰动法等[2]。近几年，基于谱分析的多项式混沌法(polynomial chaos method， PC)[3]逐渐引起人们的注意[4-9]。该方法根据与求解器的耦合方式，可分为嵌入式多项式混沌法(intrusive polynomial chaos, IPC)和非嵌入多项式混沌法(non-intrusive polynomial chaos, NIPC)。IPC需根据原控制方程建立相应的随机控制方程，无法利用现有程序，需重新研制求解程序。而NIPC不需要对控制方程进行修改，可以采用已有的数值求解程序。此方法是把已有的数值求解程序作为一个黑匣子，在随机空间里通过抽样方法，获得若干个样本点，基于各样本点输入到程序数值求解，获得输入参数各样本点的数值结果，以统计分析评估输入参数或计算条件的不确定性在计算过程中传播的影响，即给出输出结果的不确定性，以确定待定参数或计算条件。

1 数学模型

1.1 PC方法

假定参数ξ为某模型的不确定量，则可将ξ视为随机变量，因此可用概率密度函数(probability density function， PDF)表示。在工程实际中，不确定参数ξ可表示成：

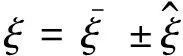
(2)

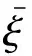
如果对模型不确定参数ξ没有更多的信息，很难给出不确定参数ξ满足的PDF。为了开展随机参数不确定性分析，最简单地可假设随机变量参数服从均匀分布或Gauss分布。均匀分布的PDF为：

(3)

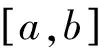
假设所求解问题的解(如爆轰压力)为u(X,t,ξ)，具有PC展开形式表示为：

(4)

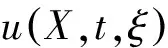
数学上，勒让德函数指勒让德微分方程的解：

(5)

勒让德多项式的一个重要性质是其在区间-1≤x≤1关于L2内积满足正交性，即：

(6)

式中：δmn为克罗内克δ记号，当m=n时为1，否则为0。相邻的3个勒让德多项式具有三项递推关系式：

(7)

(8)

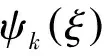
1.2 爆轰模型

爆轰数值模拟中所使用的基本方程是不定常可压缩理想流体力学方程和化学动力学方程的耦合方程组：

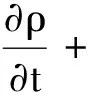
(9)

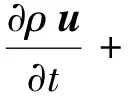
(10)

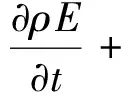
(11)

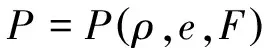
(12)

(13)

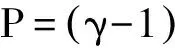
(14)

(15)

(16)

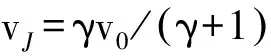
1.3PC法与爆轰产物JWL状态方程参数评估

采用式(4)对爆轰计算输入一组随机变量参数ξ1,ξ2,...,ξn，对评估的响应量(如压力、密度等)进行PC展开，则得：

(17)

利用NIPC方法进行不确定度评估的算法为:

(1)选取模型参数{ξ1,ξ2,...,ξn}的PDF，如正态分布、对数正态分布、指数分布和均匀分布等。对于爆轰模型，将其他输入参量固定，将JWL模型中参数R1和R2作为随机变量参数，PDF取均匀分布。

(2)确定模型评估的响应量在参数{ξ1,ξ2,...,ξn}的PC谱展开式(17)。

(3)对参数构成的随机变量ω={ξ1,ξ2,…,ξN}进行抽样，将其带入PC多项式中的ψk(ω(θ)),k=0,…,P，然后再计算模型参数值θ={ξ1,ξ2,…,ξN}，对每一次抽样，模型参数值为确定值。

(4)对每一抽样确定后的模型参数值，利用“确定性程序”计算得到相应的数值解u(x,t)，如第m次抽样得到解为(u(x,t))m。

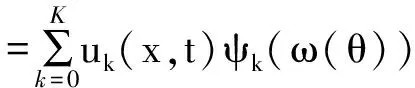
(18)

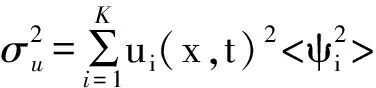
2 计算结果与讨论

利用第1节PC方法和爆轰模型，采用二维拉氏非结构自适应爆轰弹塑性流体力学程序(LAD2D)[10-11]求解，开展爆轰模型JWL状态方程待定参数不确定性的影响研究。

2.1 平面爆轰问题

图1 平面爆轰计算模型Fig.1 Computational model of plane detonation

2.2 平面爆轰问题JWL参数不确定性的影响

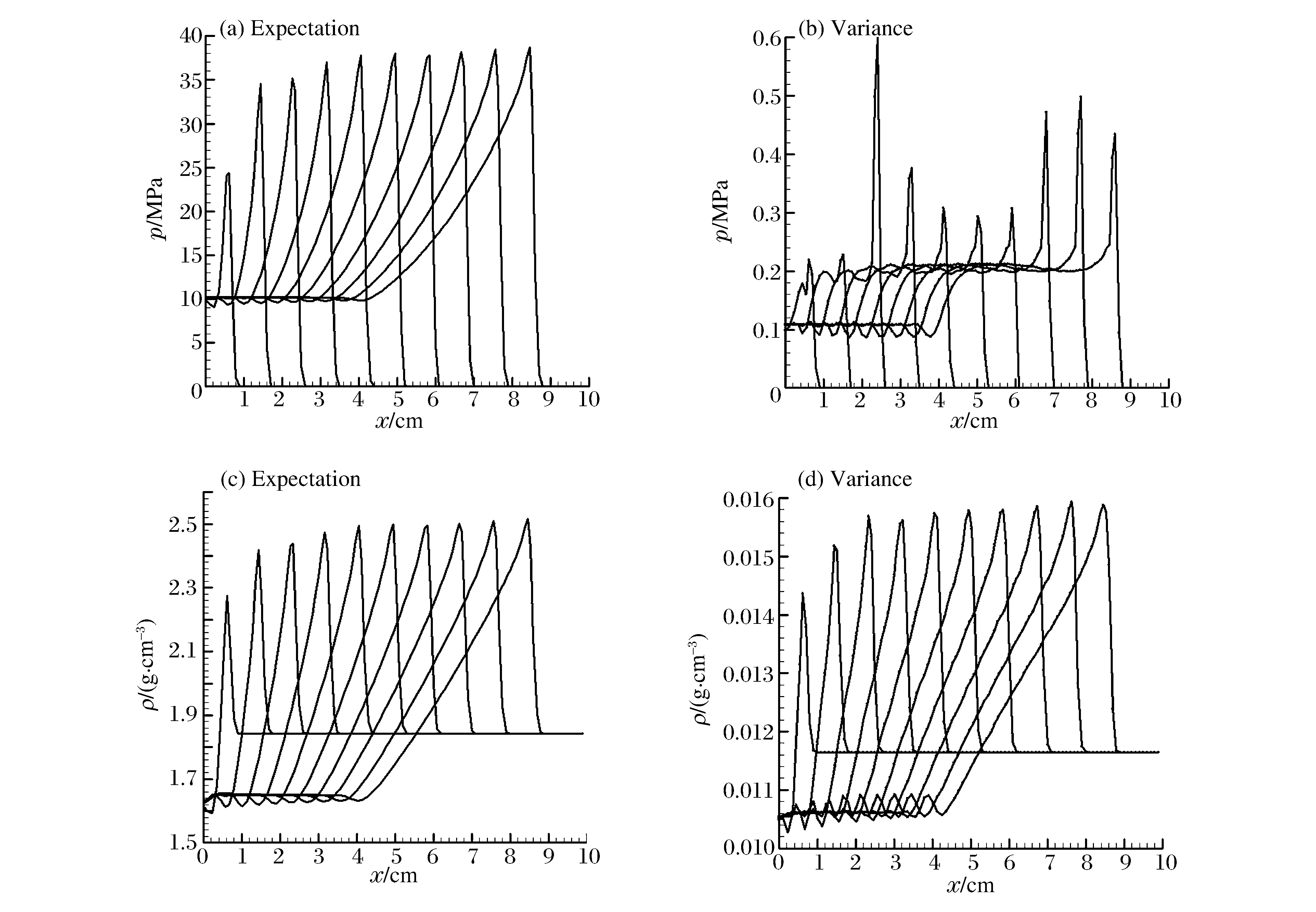
图2 R1=4.8±0.5和R2=1.95±0.5随机抽样下物理量的期望和方差Fig.2 Expectation and variance under the random-sample with R1=4.8±0.5 and R2=1.95±0.5

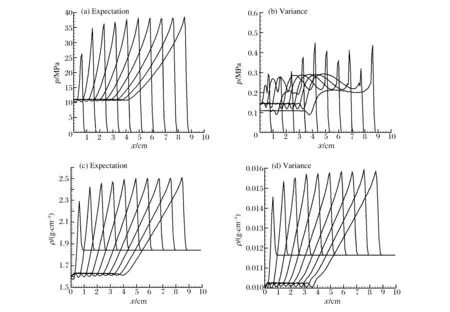
图3 R1=7.3±0.5和R2=2.46±0.5随机抽样下物理量的期望和方差Fig.3 Expectation and variance under the random-sample R1=7.3±0.5 and R2=2.46±0.5

从图2～3平面爆轰问题模拟结果可以看出，JWL状态方程不确定性参数R1、R2在2个不同区间均匀抽样，计算结果通过PC分析方差差别比较大。R1=7.3±0.5、R2=2.46±0.5比R1=4.8±0.5、R2=1.95±0.5的方差小，说明输入参数R1=7.3±0.5、R2=2.46±0.5对计算结果敏感性比输入参数R1=4.8±0.5、R2=1.95±0.5对计算结果敏感性小。说明输入参数R1=7.3±0.5、R2=2.46±0.5更合理。

2.3 散心爆轰问题

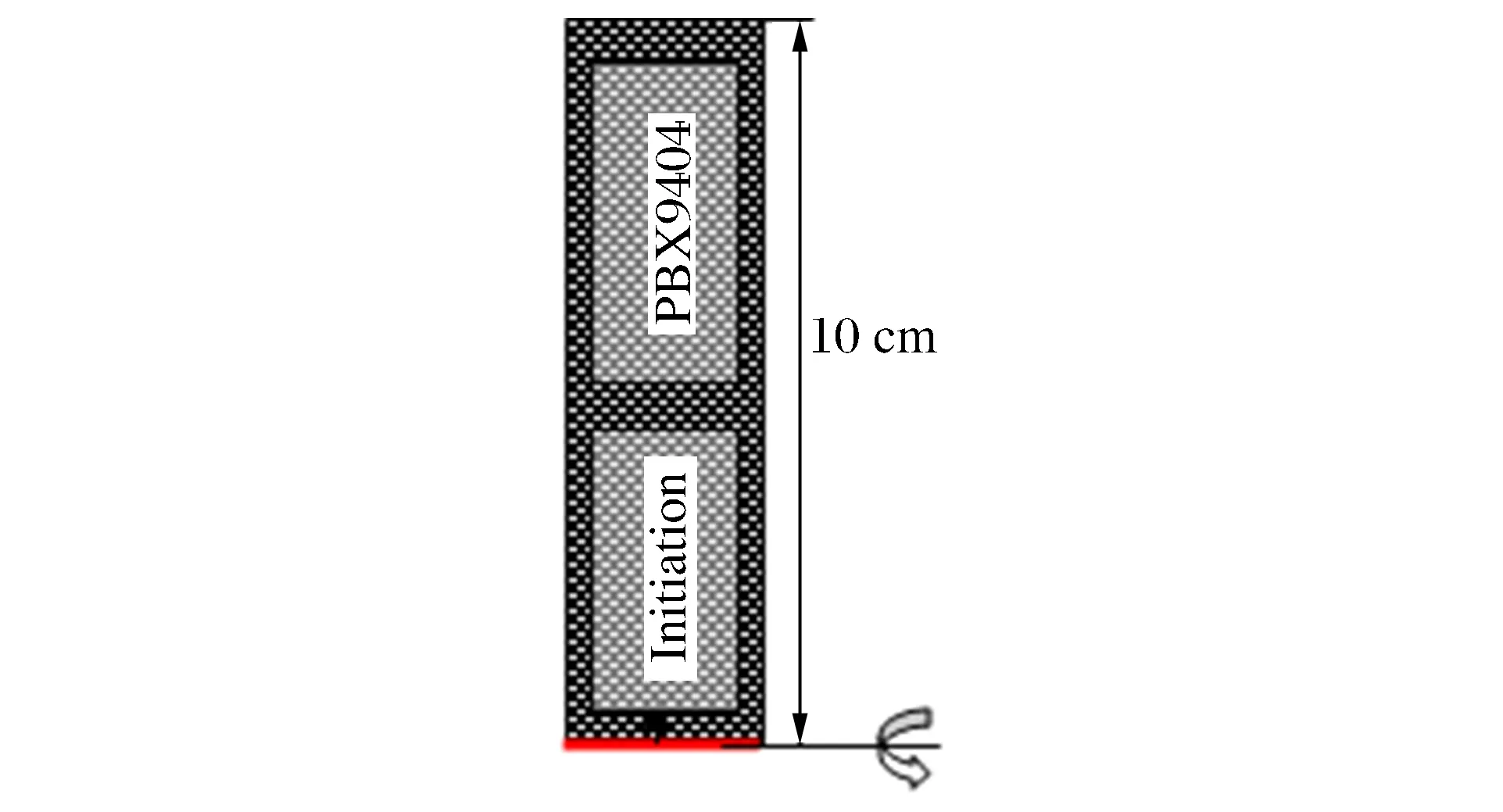
图4 散心爆轰计算模型Fig.4 Computational model of divergent detonation

2.4 散心爆轰问题JWL参数不确定性的影响

从图2、3、5、6中炸药爆轰数值模拟的结果可以看出，散心爆轰问题爆轰产物JWL状态方程参数R1、R2的不确定度对计算结果影响的不确定性，即方差比平面爆轰问题大，说明散心爆轰产物JWL状态方程参数R1、R2对计算结果敏感性强，需要引起重视。

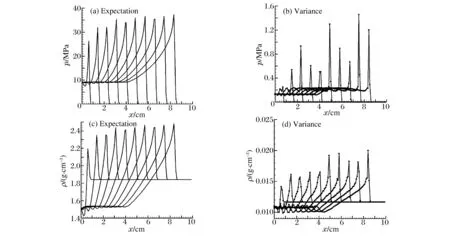
图5 R1=4.8±0.5和R2=1.95±0.5随机抽样下物理量的期望和方差Fig.5 Expectation and variance under the random-sample R1=4.8±0.5 and R2=1.95±0.5

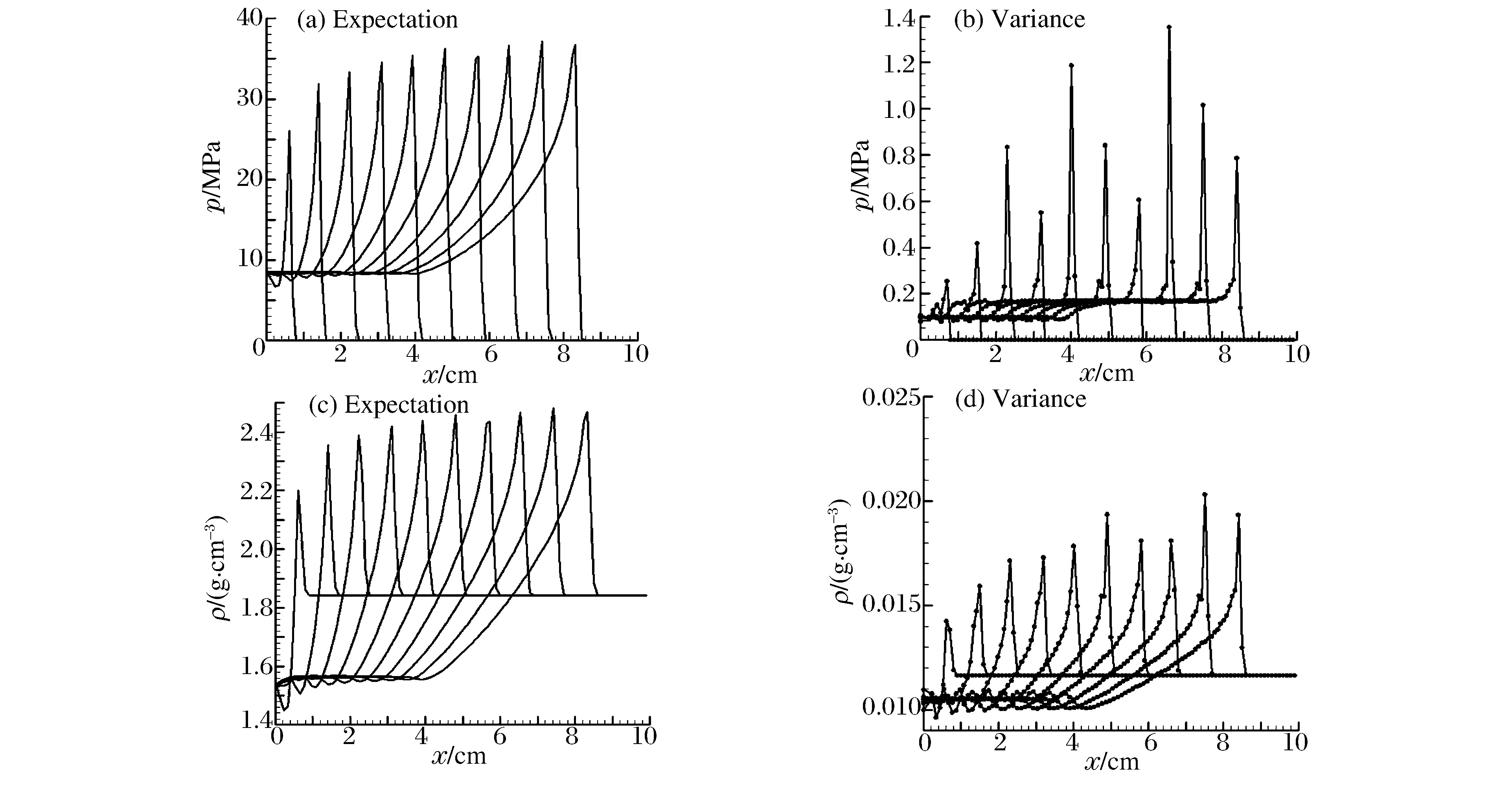
图6 R1=7.3±0.5和R2=2.46±0.5随机抽样下物理量的期望和方差Fig.6 Expectation and variance under the random-sample R1=7.3±0.5 and R2=2.46±0.5

3 结 论

(1)采用非嵌入式多项式混沌法，对JWL模型中待定参数R1、R2不确定性在爆轰数值模拟中的传播进行了研究，给出了平面、散心爆轰问题中R1、R2的不确定性对计算结果响应量(压力与密度)的期望与方差。(2)从分析结果看，散心爆轰问题爆轰产物JWL状态方程参数R1、R2的不确定度对计算结果的不确定性，即方差比平面爆轰问题大，说明散心爆轰产物JWL状态方程参数R1、R2对计算结果敏感性强，需要引起重视。 (3)多项式混沌法可以有效地量化不确定性在数值模拟中的传播，以评估参数有效范围。

[1] Green L, Lee E, Mitchell A, et al, Equations of state of PBX-9404, LX-07, RX-26-AF detonation products at pressure above detonation pressure[R]. UCRL-89664. 1983.

[2] 王瑞利，张树道，刘全，等.复杂工程M&S中不确定度量化方法进展[C]∥中国力学大会2013年论文摘要集.西安，2013.

[3] Wiener S. The homogeneous chaos[J]. America Journal of Mathematic, 1938,60(4):897-936.

[4] Maitre P O, Knio O M. Spectral methods for uncertainty quantification: With applications to computational fluid dynamics[M]. New York: Springer, 2010.

[5] Hosder S, Perez R, Walters R W. A non-intrusive polynomial chaos method for uncertainty propagation in CFD simulations[C]∥44th AIAA Aerospace Sciences Meeting and Exhibit (2006). Reno, Nedava, 2006:1-19.

[6] Knio O, Maitre O. Uncertainty propagation in CFD using polynomial chaos decomposition[J]. Fluid Dynamics Research, 2006,38:616-640.

[7] 王晓东，康顺.多项式混沌法求解随机Burgers方程[J].工程热物理学报，2010，31(3)：393-398. Wang Xiao-dong, Kang Shun. Solving stochastic Burgers equation using polynomial chaos decomposition[J]. Journal of Engineering Thermophysics, 2010，31(3)：393-398.

[8] 刘智益，王晓东，康顺.多项式混沌方法在随机方腔流动模拟中的应用[J].工程热物理学报，2012，33(3)：419-422. Liu Zhi-yi, Wang Xiao-dong, Kang Shun. Application of multi-dimensional polynomial chaos on numerical simulation of stochastic cavity flow[J]. Journal of Engineering Thermophysics, 2012，33(3)：419-422.

[9] 刘全，王瑞利，林忠，等.流体力学拉氏程序收敛性及数值计算不确定度初探[J].计算物理，2013，30(3)：346-352. Liu Quan, Wang Rui-li, Lin Zhong, et al. Asymptotic convergence analysis and quantification of uncertainty in Lagrangian computations[J]. Chinese Journal of Computational Physics, 2013，30(3)：346-352.

[10] 王瑞利,林忠,闫伟.多介质问题分析的前处理程序PreGenGrid[J].应用数学和力学,2013,5(15): 535-545. Wang Rui-li, Lin Zhong, Yan Wei. Simulations of the multi-medium problem pre-process: PreGenGrid[J]. Applied Mathematics and Mechanics, 2013,5(15):535-545.

[11] 王瑞利，林忠，倪国喜.基于任意多边形拉氏网格的有限体积方法研究及应用[J].数值计算与计算机应用，2006，27(1)：31-38. Wang Rui-li, Lin Zhong, Ni Guo-xi. Base on arbitraryn-polygon Lagrange grids finite volume method and applications[J]. Journal of Numerical Methods and Computer Applications, 2006，27(1)：31-38.

(责任编辑 曾月蓉)

Non-intrusive polynomial chaos methods and its application in the parameters assessment of explosion product JWL

Wang Rui-li, Liu Quan, Wen Wan-zhi

(InstituteofAppliedPhysicsandComputationalMathematics,Beijing100094,China)

A non-intrusive polynomial chaos method was introduced, and the main procedure of uncertainty quantification for JWL-EOS parameters was given. The method was implemented for the uncertainty quantification of the input parametersR1andR2of JWL-EOS to the detonation of plane and divergence. The results show that the methods of non-intrusive polynomial chaos can provide a valuable tool for the simulation of propagation of uncertainties, and uncertainty quantification for modeling and simulation in complex engineering.

mechanics of explosion; JWL-EOS; parameters of JWL; non-intrusive polynomial chaos; uncertainty quantification

10.11883/1001-1455(2015)01-0009-07

2013-06-24；

2013-09-10

国家自然科学基金项目(11372051,11072039,11201035); 中国工程物理研究院科学技术发展基金项目(2013A0101004)

王瑞利(1964— )，男，研究员,wang_ruili@iapcm.ac.cn。

O385 国标学科代码： 13035

A