基于结构信息和稀疏贝叶斯学习的图像去噪
刘 帅
(西安电子科技大学 西安 710071)
0 简介
在图像处理中,如何用空间变换有效地表达图像信息,是一个很重要的问题。传统的图像表示方法是基于“基”的展开,如Fourier 变换和小波变换等。但这种建立在正交基上的信号分解有一定的局限性,往往不总能够达到好的稀疏表示效果,尤其是对于变化范围很大的图像,效果更差。一种更好的图像处理方法应该是根据图像的特点,自适应地选择合适的基函数,来完成图像的稀疏分解。因此近年来非正交分解引起人们极大的研究兴趣。超完备信号稀疏表示方法肇始于Mallat 和Zhang 于1993年提出基于冗余字典(redundant dictionary)的稀疏分解思想[1]。
2004年由Candes,Romberg,Tao 和Donoho[2]建立起来的压缩传感(Compressive sensing,CS)理论进一步将稀疏表示思想提升到了一个新的高度。CS理论的基础就是要求信号在某个空间具有稀疏性,因此稀疏表示的研究有极其重要而深远的理论意义和广泛的应用价值。目前稀疏表示已在图像去噪和修复[3-5][7-10]、CS 等领域取得广泛应用。
图像稀疏表示理论中的一个关键问题就是如何设计有效的稀疏表示过完备字典。本文采用非参数贝叶斯方法[13,14]来构造和学习冗余字典来实现图像去噪和修复,该方法可以可以更全面的捕捉诠释图像信息,实验结果表明,基于非参数贝叶斯的字典学习方法在图像去噪和修复方面具有良好的性能。
1 基于的稀疏贝叶斯学习的冗余字典学习
1)D 是给定的,通过点估计来推断a,常用的有OMP,BP 等,这些算法的停止准则一般是假设一噪声值或者对a的稀疏性进行约束;
2)通过学习得到字典D,但是需要预先设定字典的原子数M。
通过对已有的方法进行分析,文中采用非参数贝叶斯方法来进行学习。该方法可以同时推断字典原子数M 和a;另一方面,相比于之前的点估计方法,该方法可以得到参数的完整后验分布。同时,图像本身固有一定的结构信息,本文将结构信息作为先验,约束所构造冗余字典的更新,以更好的捕捉图像本身的固有特性。
1.1 结构信息
图像本身具有一定的结构信息,为了更好地实现图像处理,有效地应用捕捉结构信息,就变得非常重要。本文采用Zhou Wang 等提出的结构信息计算方法,并将其作为字典的先验信息,对字典进行约束更新。具体计算方式如下:
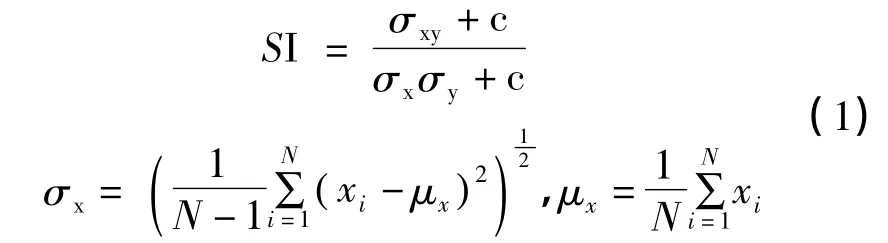
其中c 为一个常数。
1.2 Beta 过程框架
近几年,基于非参数贝叶斯的应用研究越来越火热。文中采用了基于Beta 非参数贝叶斯方法,假定实验模型为:x= Da+ε,其中x∈Rn、D∈Rn×m,为了实现在学习字典D的过程中推断字典大小M的目的,假定D∈Rn×K,在此假设K→∞,然后通过推过推断字典D所包含的列数(即原子数)来近似的确定字典大小。我们希望求得的α ∈RK是稀疏的,即α 中除却有限项外其余均为0,因此字典D中仅有一小部分原子被用来表示x。这里仅讨论文中所用到的beta过程的部分原理。两参数的beta过程是一个非参数的先验。定义为H ~BP(a,b,H0),其中H0为0~1 区间的一致分布Uni(0,1),a>0,b>0。上述分布又可以表示为:
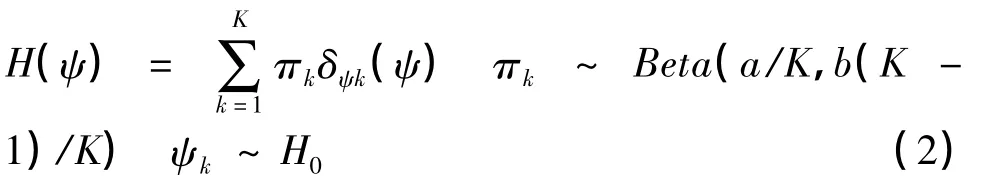
当ψ=ψk时,δψk(ψ)等于1,否则δψk(ψ)等于0。有此可见,H(ψ)代表了每一个原子ψk是否被使用的K中可能性。在K→∞时,H(ψ)就成为一个表示无限维概率的矢量,其中相应于每一个ψk的概率满足ψk
iid ~H0。
为了便于应用H(ψ),我们定义了N位二进制矢量zi ~{0,1}K,其中i=1,2,…,N,zi的第k个分量满足zik ~Bernoulli(πk)。由这N个二进制列向量组成了指示矩阵Z,且Z ~{0,1}K×N,因此Z的第i列表示zi,Z的第k行则相应于原子ψk。在待处理问题中,原子ψk∈Rn代表了字典D的候选集中的成员,二进制矢量zi则表示对样本xi使用了字典D中的哪些原子进行近似表示。
假设Ψ={ψ1,ψ2,…,ψk},K→∞,则样本xi可以表示为xi=Ψzi+ε,但是这种经典的表示是有着高度限制的,因为他要求字典的系数必须是二进制的。为了解决这一问题,我们引入权值矩阵W,W∈RK×N,其中wi ~N(0,γ-1w IK),i=1,2,…,N,γw表示高斯分布的方差。则字典权值ai= zi·wi,符号·表示哈德曼乘积。从ai的构建过程可以发现,ai是稀疏的。另外,不同于广泛使用的拉普拉斯先验,使用拉普拉斯先验得的稀疏系数除却非少数相对来说比较大的系数外,其余系数则非常小;而拟议模型得出的稀疏系数除却非0 项则是直接等于0。这样就可以直接求解零范数。
为了计算方便,我们假定字典元素ψk服从多变量的高斯分布;在独立同分布的准则下拟议模型如下所示:
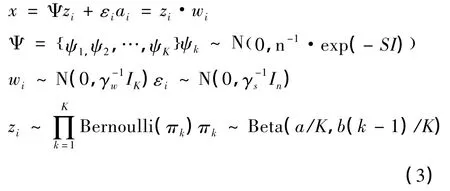
γε、γw由满足非信息先验的Gamma 分层先验来确定。同时,可以发现,上面模型具有共轭对称性,因此可以应用吉布斯采样来进行分析推断字典D 以及字典大小M。
1.3 顺序字典学习
在上面的讨论中,我们是使用所有的数据一起来学习推断字典D,然而,在某些应用中,N 可以能是想当大的,出于对复杂度、时间等方面的考虑,法同时学习的方法就太好了。为了解决这一问题,我们将数据分割为,依次采用beta 过程对其进行处理。算法的收敛性和详细描述见[15]。假定表示理想字典的后验概率,矢量Θ 代表拟议模型的所有分层参数。在贝叶斯分析中,先通过推断,将求解结果作为先验然后来推断。依次类推,最终来实现推断的目的。
2 图像去噪
图像信号在处理过程中,通常会受到图像噪声的影响,导致图像处理不能满足后续分析处理的要求。为了保证图像的视觉效果,研究出有效的去噪算法,是十分必要的。以达到能从被污染的图像中获取原图像真实信息,并且将图像处理过程中对图像本身的干扰降低到最小,为以后对图像进行进一步的处理做好准备。另一方面,图像在传输过程中经常会发生数据丢失,解压后会有块状图像信息缺失的现象;或者是原始图像上面有了一些不期望的内容(如文字),这种情况下就需要最大限度近似恢复原始图像。
假定待处理图像为I∈RNy×Nx(这里以灰度图像为例,彩色图像类似,见结果展示),图像噪声是加性的。我们见将图像分割为个重叠的块。对于任意一个xi,满足xi∈RB2,文中使用的是B=8。
如果只有加性噪声,而没有消失像素,则可以直接使用模型()来同时进行字典学习和图像去噪。如果既有噪声,又有消失像素,我们不再像之前那样直接观测xi,而是观测它的子集。注意到用来恢复原始无噪完整图像的ψ 和是从待测数据集直接推断的,因此这里也可以使用数据集离线学习字典D。
通常图像去噪,如[16,17],通常预先要设置一个停止准则,或者是对某一变量值进行约束、或者是对稀疏度等。这种方法在通常是很有效的,但是如果不需要预先做出这一假设,应该是更好的。文中的拟议模型则不需要做出这种设定。该模型假设噪声γε服从非信息Gamma 分布,然后通过他的后验概率对其推断;稀疏表示的稀疏度则满足由参数a 和b 控制的Beta 分布。因此可以从数据本身求解出系数表示的平均稀疏度。上面都是以黑白图像为例,如果是彩色图像,也很容易,只需要将3 通道的参数分别设置就好。以γε为例,只要对三通道里的每一个B×B 块分别假设一个γε,且这三个γε的Gamma 先验相同就好。
3 实验结果
通过实验表明,对于图像去噪和修复,采用吉布斯采样推断比采用变分贝叶斯推断所得的结果更好。因此文中所有推断均采用吉布斯采样推断。图像去噪和修复过程中所用的分层参数值设置时一样的,所有的Gamma 先验设置为Gamma(10-6,10-6),Beta 分布的参数为a=K 和b=N/8(设置为其它值产生的结果相似)。
文中对各个实验图像分别加方差为15、20、50的噪声,用以下四种方法进行图像去噪:(1)采用非信息先验的基于BP 字典的非参数贝叶斯算法,所有的去噪图像采用一样的BP 模型;(2)K-SVD 算法,其中噪声方差大小设定为图像所加噪声方差;(3)K-SVD 算法,其中噪声方差大小设定为图像所加噪声方差不同的值;(4)基于DCT 字典的图像去噪算法。下面的实验结果给出了加噪声后的图像,和用算法处理后的对比图,以及相应的数值比较。
下面三组图像第一行第一幅代表原始图像,第二幅为加方差为15 的高斯白噪声后的噪声图像,第三幅为拟议算法的结果,第四幅为拟议算法的学习字典;第二行第一幅图像为DCT 字典的结果;第二幅为KSVD 字典的结果,第三幅和第四幅分别为DCT 和KSVD 的学习字典。

下面三组图像第一行第一幅代表原始图像,第二幅为加方差为20 的高斯白噪声后的噪声图像,第三幅为拟议算法的结果,第四幅为拟议算法的学习字典;第二行第一幅图像为DCT 字典的结果;第二幅为KSVD 字典的结果,第三幅和第四幅分别为DCT 和KSVD 的学习字典。
下面三组图像第一行第一幅代表原始图像,第二幅为加方差为25 的高斯白噪声后的噪声图像,第三幅为拟议算法的结果,第四幅为拟议算法的学习字典;第二行第一幅图像为DCT 字典的结果;第二幅为KSVE 字典的结果,第三幅和第四幅分别为DCT 和KSVD 的学习字典。

5 总结
稀疏性在图像处理过程中的作用越来越重要。文中在自然图像的去噪和修复中,用基于Beta-Bernoulli 过程的非参数贝叶斯字典来实现图像的稀疏。相比于已有算法,实验表明,该算法有以下重要优势
1)不需要预先知道噪声值,而是在分析的过程中推断早噪声,以实现去噪;
2)可以推断完整的后验概率,因此可以用error bar 对结果进行分析;
3)尽管可以用训练数据来初始化字典,但是本文的BPFA 采用随机初始化就能得到很好的实验结果。
当然,通过文中分析可以发现,拟议模型可以用于CS 问题中,当然也包括一些逆问题。有此可见,该算法在图像处理中具有一定的优越性。
[1]Mallat S.G Zhi feng Zhang Matching Pursuit with Time-frequency Dictionaries[J].IEEE Trans on Signal Processing,1993,41(12):3397-3415.
[2]David L,Donoho D.Compressed Sensing[J].IEEE Trans on Information Theory,2006,52(4):1289-1306.
[3]M.Aharon,M.Elad,and A.M.Bruckstein.K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation.[J].IEEE Trans.Signal Processing,2006,54:4311-4322.
[4]M.Elad and M.Aharon.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Trans.Image Processing,2006,15:3736-3745.
[5]J.Mairal,F.Bach,J.Ponce,and G.Sapiro.Online dictionary learning for sparse coding.In Proc[M].International Conference on Machine Learning,2009.
[6]J.Mairal,F.Bach,J.Ponce,G.Sapiro,and A.Zisserman.Supervised dictionary learning.In Proc[M].Neural Information Processing Systems,2008.
[7]J.Mairal,F.Bach,J.Ponce,G.Sapiro,and A.Zisserman.Non-local sparse models for image restoration[M].In Proc.International Conference on Computer Vision,2009.
[8]J.Mairal,M.Elad,and G.Sapiro.Sparse representation for color image restoration[J].IEEE Trans.Image Processing,2008,17:53-69.
[9]J.Mairal,G.Sapiro,and M.Elad.Learning multiscale sparse representations for image and video restoration[J].SIAM Multiscale Modeling and Simulation,2008,(7):214-241,2008.
[10]M.Ranzato,C.Poultney,S.Chopra,and Y.Lecun.Efficient learning of sparse representations with an energy-based model[M].In Proc.Neural Information Processing Systems,2006.
[11]E.Cand`es and T.Tao.Near-optimal signal recovery from random projections:universal encoding strategies IEEE Trans.Information Theory,2006,52:5406-5425.
[12]J.M.Duarte-Carvajalino and G.Sapiro.Learning to sense sparse signals:simultaneous sensing matrix and sparsifying dictionary optimization[J].IEEE Transactions on Image Processing,2009,1395-1408.
[13]R.Thibaux and M.I.Jordan.Hierarchical beta processes and the indian buffet process[M].In Proc.International Conference on ArticialIntelligence and Statistics,2007.
[14]J.Paisley and L.Carin.Nonparametric factor analysis with beta process priors.In Proc[M].International Conference on Machine Learning,2009.
[15]J.Mairal,F.Bach,J.Ponce,and G.Sapiro.Online dictionary learning for sparse coding[M].In Proc.International Conference on Machine Learning,2009.
[16]M.Elad and M.Aharon.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Trans.Image Processing,15,2006.
[17]J.Mairal,M.Elad,and G.Sapiro.Learning Multiscaes Sparse representation for image and video restoration[J].IEEE Trans.Image Processing,2008,2(1):2014-241.

