一种小角度误差快速检测方法及不确定度分析

孙斌，李云玲，卜雄洙

(1.南京理工大学机械工程学院，江苏南京210094;2.内蒙古北方重工业集团有限公司，内蒙古包头014033)

0 引言

转台常常作为高精度的角度位置产生的基础平台。转台的位置输出精度直接影响整个测试系统的校准或测量精度，因此需要经常对转台的角度系统进行误差测量，为调校转台设备提供依据。传统的机械测角法有多面体棱镜法、分度台法等;近些年来又研究出较多的光学测角法，如圆光栅法、衍射法、以及激光干涉法等［2］。机械方法自动化程度低、操作繁复且多只能用于静态测量。光学法虽然操作简便、自动化程度高，但实验设备复杂、昂贵，设备通用性差，对环境要求严苛［3］。在存在振动等干扰的环境中，无论是传统的机械测角法还是高精度的光学测角法都很难实施，即使条件允许，测量过程往往过于繁复。因此，研究具有较强环境适应性的快速测量方法很有必要。自准直经纬仪是最常用的光学测角仪器之一，具有自动补偿机构，能很好地适应不同的应用环境，常用于大地观测、微小角度测量等领域。本文以单轴俯仰转台为例，针对传统角度误差检测设备难以对转台角度误差进行快速测量的问题，提出一种适合于现场快速应用的自准直经纬仪对准静态误差测量方法，并建立其误差测量模型，推导模型解算的方法，最后对其测量不确定度进行评定。

1 测量原理及系统组成

1.1 测量原理

利用自准直经纬仪测量转台角度误差的原理如图1所示，反射面做以转台水平轴中心O 为旋转中心的同轴转动。测量时，先转动转台水平轴至预设角度误差测量位置θ，反射面跟随其同步转动，调整自准直经纬仪，使其发出的光线经反射面垂直反射后成自准直像，即返回的十字像落在固定分划线的双十字刻线中心，然后读取经纬仪上垂直角φ，根据光路可知，θ=φ-90°，结合转台自身角度输出θ’，就可以得到该位置下转台的角度误差，记录结果并开始下一次测量，按照此步骤依次完成各个预设角度位置的误差测量。

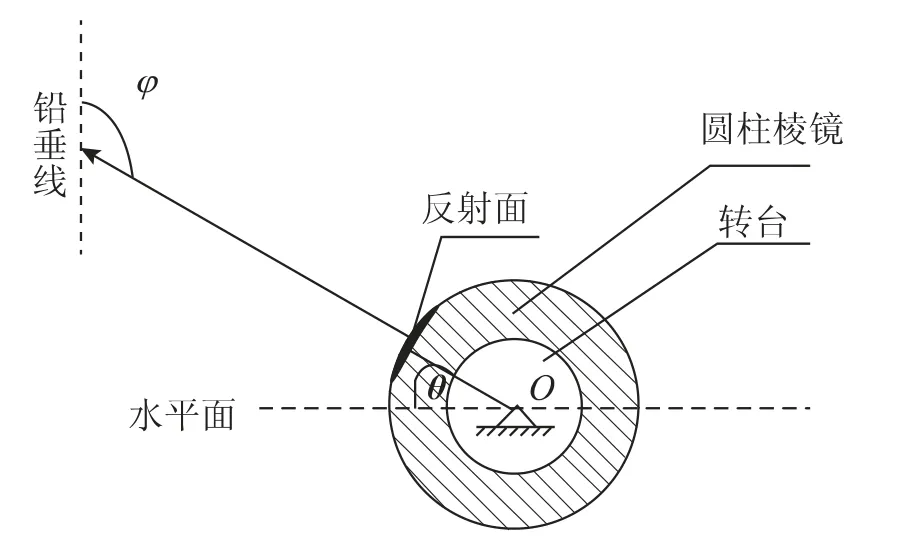
图1 角度误差测量原理图

1.2 系统组成

采用自准直经纬仪对准法进行静态误差测量的装置如图2所示，该套测量装置主要由自准直经纬仪、反射棱镜和上位机等组成。自准直经纬仪因其测量精度高、操作简单及可靠性好等特点在高精度安装和方向基准建立中得到广泛应用。一般电子经纬仪的测角精度能达到秒级［4］，对于一般转台的角度误差测量而言已足够。反射棱镜是由圆柱体棱镜在其侧面加工出一个镀膜反射面，如图2 中面A所示，镀膜的目的是提高反射率。安装时，首先用分度值为0.0002 mm 的测微表来找正，调整定位夹具的芯轴与被测转轴中心重合。在此基础上，在转台处于水平时，用高精度光电准直仪水平将反射面的中心法线调整至水平，即反射面处于铅垂，至此反射棱镜安装完毕，之后的测量过程中无需再调整。上位机主要完成测量控制、数据采集处理及结果显示的工作，数据包括转台自身的转动角度输出以及自准直经纬仪的角度输出。该套设备构成简单，实用性强。针对不同的转轴，只要加工相应的工装使得反射棱镜能够同轴安装即可，通用性明显优于其他一些光学方法。

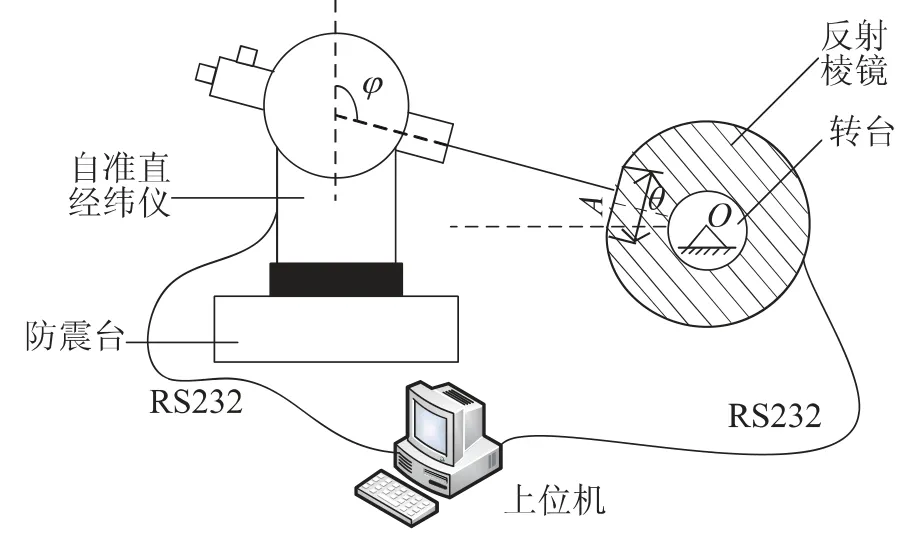
图2 自准直经纬仪测量转台误差装置示意图

2 空间反射模型及解算方法

2.1 空间反射模型

转台转角误差测量的反射模型如图3所示。为了更准确地描述测量过程，选取参考坐标系OXYZ，矢量A，A'和N 分别为反射平面的入射光矢、反射光矢和反射面法线的单位矢量。图3 中，φ 角为反射平面的入射光线A 与Z 轴的夹角，即自准直经纬仪的垂直角输出;α 角是入射光线A 在XY 平面投影Axy与Y 轴的偏移角;θ 是反射棱镜反射面中心法线N 与水平线的夹角，测量过程中以转台自身的角度输出近似表示;β角是反射面法线N 在XZ 平面投影Nxz与Z 轴的偏移角。理想情况，φ，θ 处于YZ 平面且满足θ=φ-90°，此时有α=β=0°，问题简化为二维模型。但是实际测量时，由于安装误差、仪器误差、人员误差等的存在，α，β 均不为0 且两者间不存在明显的数学关系，此时φ，θ 不再满足θ=φ-90°的关系。所以绝大多数情况下，简化的二维模型不能反映实际测量中存在的许多误差来源，即二维模型只能用于定性说明测量原理，无法用于实际测量。

图3 空间反射测量示意图

为了解决上述问题，需要研究建立三维空间反射测量模型。结合光线的矢量性，采用矢量分析方法［5］建立的模型关系式为

2.2 模型解算

在图3所示坐标系下可得

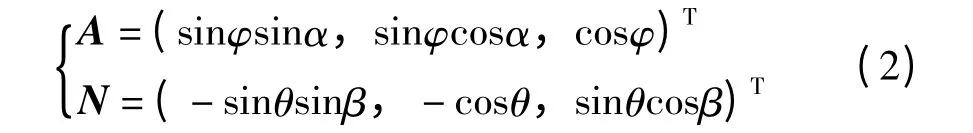
测量时，调整自准直经纬仪使其成自准直像，即光线是原路返回，则

结合式(1)，(3)可得

将式(2)代入式(4)并化简可得

式(5)说明此时φ，θ 为非线性关系，且与偏移角α，β 大小有关，α，β 的地位对等。图4 是角α，β 存在下θ 与理论真值的误差。

图4 偏移角α，β 对测量结果的误差

从图4 可知，当cosα，cosβ 的值都接近1，即α，β接近0 时，偏差很小，这时可以进一步化简式(5)可得

从式(6)得到了与二维平面分析一致的表达式。所以，当测量装置安装调校比较好的情况下，如果要求的测量精度不是很高，可以采用式(6)作为测量的反射模型。否则，采用式(5)更为合适，但是需要额外的增加对偏移角α，β 的测量，增加了实验操作难度。

3 不确定度评定

3.1 数学模型

实验被测对象为一台A1-ST14A-JX-00 单轴电动俯仰转台，其位置误差指标在15″以内，自准直经纬仪采用的是DT202C 电子经纬仪，垂直角测角误差为2″，满足测量不确定度之比在1/4 ～1/10 的条件［6］，所以选择式(6)作为角度误差测量的反射模型。在该条件下，角度误差可以表示为

式(7)中φ 与θ'相互独立，故由不确定度传播律得合成标准不确定度的平方为

式中:cφ，cθ’为灵敏系数，。

3.2 不确定度分量评定

3.2.1 自准直经纬仪读数φ 相关误差引入的不确定度

1)测量重复性引入的不确定度

实验预设测量位置为-10° ～+20°，间隔2°，一共16 个测量点。设备安装调节完后，通过各6 次盘左、盘右对预设角度位置进行重复测量，单次测量的标准不确定度s(x)=2.06″。故测量重复性引入的标准不确定度为

自由度ν1=n-1=5。

2)自准直经纬仪引入不确定度

自准直经纬仪引入误差包含仪器误差和对准误差两部分。仪器误差通过查产品合格证书:U=1″，k=2，可得不确定度分量

u2=1/2=0.5″

相对不确定度为90%，则自由度ν2=50。

对准误差主要是由人眼的分辨力限制造成的。实验所用自准直经纬仪望远镜放大率为30，对准方式为压线对准和夹线对准相结合，其人眼分辨误差约为δ=15″［7］，所以其对准误差的不确定度分量为

u3=15″/30=0.5″

相对不确定度为80%，自由度ν3=12。

3)反射棱镜引入不确定度

反射棱镜引入误差包括反射棱镜反射面的面形误差及其安装误差。反射平面并不是绝对的平面，因此其法线方向会有微小的变化。实验所用反射棱镜的镀膜反射面面形误差为高光圈N=1，所以由其造成的角度测量不确定度分量［8］为

式中:λ 为光波波长，取λ=5×10-4mm;l 为反射面的长度，l=100 mm。将弧度转为角秒得

相对不确定度为80%，自由度ν4=12。

反射棱镜采用光电自准直法［9］安装至转台轴上，转台的零位调校也是用光电自准直仪法。所采用的准直光管误差为±1″，反射面法线与转台零位线之间的安装误差最大值为2″，其分布按均匀分布［10］，则由安装误差引入的不确定度为

相对不确定度为75%，则自由度为ν5=8。

以上引入各不确定度分量的因素互不相关，所以由这些分量得到与φ 相关的标准不确定度分量为

3.2.2 转台测角系统输出角度θ'误差引入的不确定度

采用多面体棱镜法测量得到转台自身输出角度存在误差［11］，由其引入的不确定度为

式中:σmax和σmin分别为用多面体棱镜法测得的最大和最小偏差。实验所用多面体棱镜为二十三面体［12］，自由度为ν6=m-1=22。

3.2.3 合成标准不确定度及扩展不确定度

将uφ，uθ'的值代入公式(8)，可得系统的合成标准不确定度为

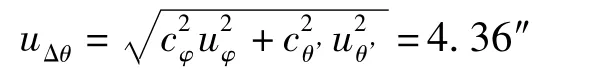
有效自由度［13］为

取置信概率为95%，查t 分布表得t95(32)=2.04，则扩展不确定度为

4 结论

本文介绍了一种利用自准直经纬仪快速测量转台转角误差的方法——自准直经纬仪对准法，通过深入分析该方法所采用的空间反射模型，给出了精确表达式，为以后进一步提高该方法精度提供了理论依据。对测量装置的不确定度评定结果表明，扩展不确定度在10″以内，能够满足转台小角度范围测量误差的精度要求。该方法与传统方法相比具有操作简便、成本低、抗环境干扰强的优点，具有工程应用价值。

［1］曾鸣，王锦贺，张健，等.转台测角系统标定方法的研究［J］.中国惯性技术学报，1998，6(4):84-88.

［2］黄仙锦，卜雄洙，杨波，等.自准直经纬仪测角系统及不确定度分析［J］.计量技术，2013(8):13-16.

［3］孙安斌，马骊群，曹铁泽，等.室内GPS 发射器角度校准装置的设计与分析［J］.计测技术，2013，33(6):35-39.

［4］刘凯.新型光电自准直经纬仪关键技术研究［D］.北京:北京交通大学，2012.

［5］樊春丽，崔莹.六面体转鼓分度和塔差的检测方法及测量结果不确定度的评定［J］.红外与激光工程，2008，37(增刊):337-339.

［6］韩素超，高雪，李红菊，等.专用分度头校准方法探讨［J］.计测技术，2015，35(S0):32-33.

［7］杨双燕.光束的矢量性表征及其应用［D］.上海:上海大学，2014.

［8］马峰，周骏.角度块角度偏差测量值的不确定度评定［J］.计量与测试技术，2015(1):44-45.

［9］何海霞.基于光电自准直的二维小角度测量技术研究［D］.武汉:湖北工业大学，2009.

［10］国家质量监督检验检疫总局.JJF 1210-2008 低转速转台校准规范［S］.北京:中国计量出版社，2008.

［11］Liang W Y，Dong J W，Wang H Z.Directional emitter and beam splitter based on self-collimation effect［J］.OPTICS EXPRESS，2007，15(3):1234-1239.

［12］Cheng Fang，Fan Kuangchao.Linear diffraction grating interferometer with high alignment toleranceand high accuracy［J］.APPLIED OPTICS，2011，50(22):4551-4556.

［13］Zhao Lirong，Zhu Wei，Zhang Yaoyu，et a1.The Method of the System Error Modification of Photoelectric Theodolite of T Type［C］//2012 International Conference on Optoelectronies and Mieroeleetronics.Changchun.Jilin:IEEE，2012:384-387.