基于改进的布谷鸟搜索光伏电池模块参数识别与仿真①

李国成

(皖西学院金融与数学学院，安徽 六安237012)

0 引 言

近年来，随着化石燃料价格的飙升以及大气污染的日趋严重，可再生能源的开发和使用得到迅速发展，其中太阳能光伏发电系统尤为突出［1］.构建准确刻画光伏电池电气特性的模型是光伏电池系统研究中一项非常重要的工作.目前实际应用中最为常见的是单二极管模型和双二极管模型［2］.刻画其电流和电压关系的函数是分别包含5 个和7个未知参数的非线性函数.精确标定这些模型参数在光伏电池模块系统的仿真模拟、性能评价、优化设计和实时控制等研究中显得尤为重要.

光伏电池模块参数识别的方法主要有解析法、传统的数值优化方法和启发式搜索算法［3～8］.光伏电池模块参数识别是一个多变量、多峰值且具有多个局部极值的非线性函数优化问题，故解析法和传统的优化技术很难对其实现精确提取［5］.而启发式搜索方法，如模式搜索(Pattern Search，PS)［5］，模拟退火算法(Simulated Annealing，SA)［6］，和声搜索(Harmony Search，HS)［7］，人工蜂群优化(Artificial Bee Swarm Optimization，ABSO)［8］等，却能以较低的时耗和更高的概率提取到更为精确的光伏电池模型参数［5］，进而更为准确地描述其电气特性.

光伏电池的非线性特性使得其对优化技术的性能有着很高的要求，特别是在勘探和开发之间的平衡能力.为此，本文将探索基于仿生学的布谷鸟搜索和基于模型的交叉熵全局随机优化方法的融合算法，开发出一种新的具有高性能的优化技术，来实现对光伏电池模块参数的精确提取，从而更为准确地刻画光伏电池模块的电气特性，以便更好地开发和利用太阳能.

1 光伏电池的物理机理和数学模型

光伏电池的电流－电压及功率－电压等电气特性是随光照强度、温度变化的非线性曲线，其等效电路模型在许多文献中各有不同，但在实际应用中一般采用单二极管和双二极管模型，以下简单介绍它们的物理模型和数学描述.

1.1 双二极管模型

双二极管光伏电池的物理模型如下图1 所示.

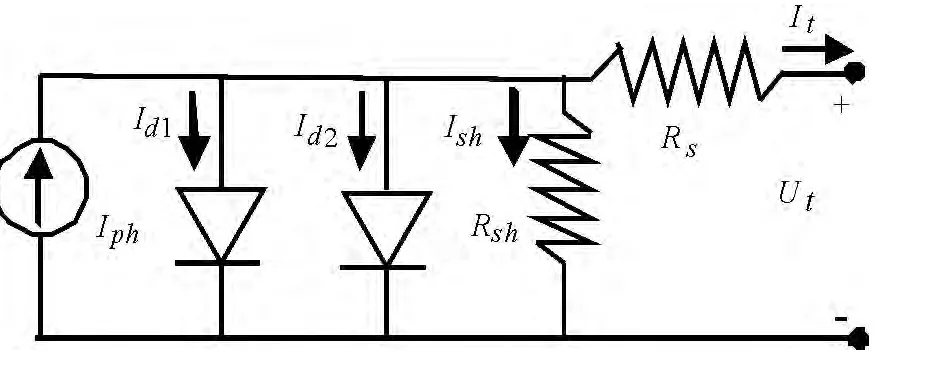
图1 双二极管光伏电池模型

设其输出电流为It，则其计算式为［8］:

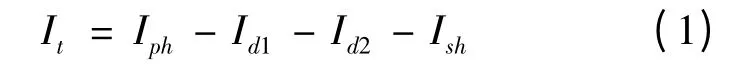
其中，Iph为光生电流，Ish为流经并联电阻Rsh的电流，Id1和Id2分别为两个二极管电流，Rs为串联电阻.对于Id1和Id2，根据Shockley 方程可得:

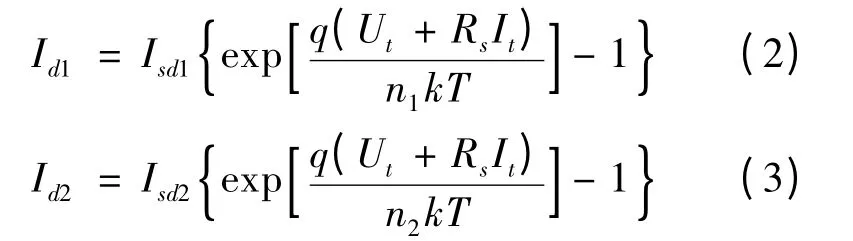
其中:Ut为光伏电池输出电压，Isd1和Isd2分别为流经两个二极管的反响饱和漏电流，T 为光伏电池的工作温度，q 为电荷电量，k 是Boltzmann 常数，n1和n2为二极管的理想常数，其值一般在1 ～2 之间变化.分流电阻的电流的计算式为:

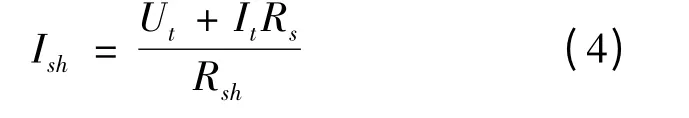
将(2)～(4)式代入到(1)式则可得光伏电池的输出电流.该模型中Rs，Rsh，Iph，Isd1，Isd2，n1和n2等七个未知参数需要标定.

1.2 单二极管模型

单二极管模型物理等效电路如下图2 所示.

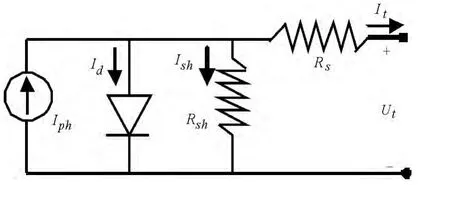
图2 单二极管光伏电池等效电路

该模型的输出电流It:

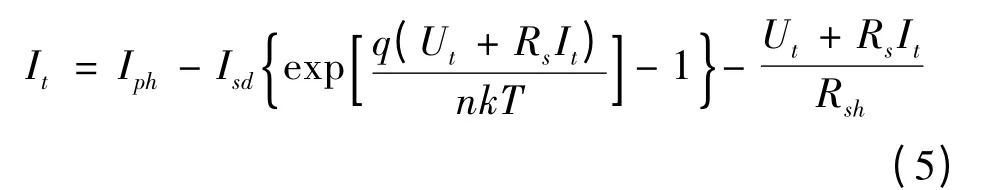
该模型五个未知参数为Rs，Rsh，Iph，Isd和n.

2 光伏电池模块参数识别

如前所述，用来模拟光伏电池模块的模型(1)和(5)中的未知参数可以在获得光伏电池系统的U－I 或U－P 实验测试数据的基础上借助于适当的优化技术来加以识别，参数识别问题转化为优化问题，其决策变量x1= (Rs，Rsh，Iph，Isd1，Isd2，n1，n2)T和x2=(Rs，Rsh，Iph，Isd，n)T由模型的未知参数所构成，优化目标函数定义如下:

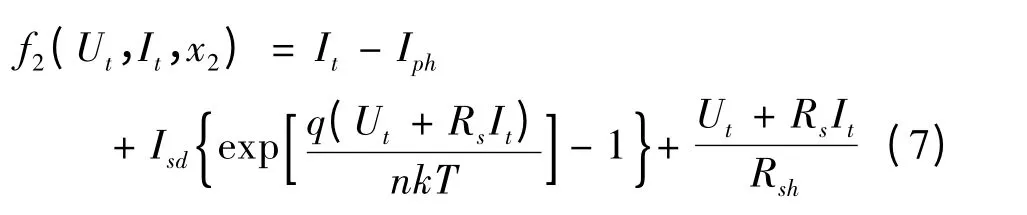
给定一个候选解x，对于真实系统每一个离散点的采样数据(Ut，It)(t=1，2，…，N)，利用以上(6)式或(7)式均可计算得到一个目标函数值.本文采用均方根误差(RMSE)来对解的优劣进行评价，其定义如下:

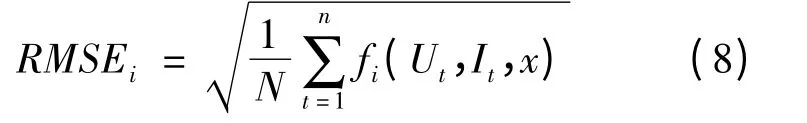
其中i=1，2 分别对应着光伏电池模块的双二极管和单二极管模型，N 为离散采样点个数.由此可得优化模型为:

其中D 为各参数的取值范围所构成的解空间，各参数的上下界参考文献［5 ～8］，具体如下表1 所示.

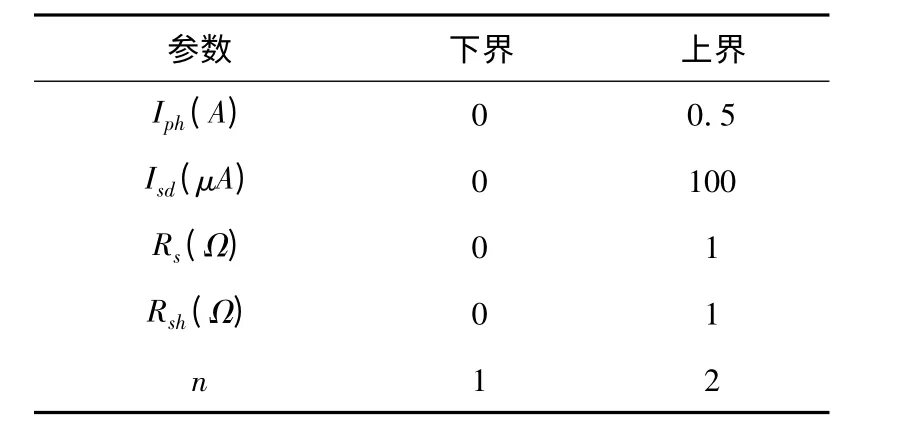
表1 光伏电池模型各参数的值域

3 改进的布谷鸟搜索

3.1 布谷鸟搜索

布谷鸟搜索(Cuckoo Search，CS)是Yang 和Deb 于2009 年提出的一种新的仿生算法［9］.该算法从布谷鸟的寄宿繁衍后代的生物习性提炼出三个理想化规则进而形成一种优化工具，在工程优化中取得较好的应用效果［9～10］.其规则如下:

(1)每只布谷鸟随机选取一个宿主鸟巢并产下一枚卵，该卵代表着优化问题的一个候选解x;

(2)位置较好的宿主鸟巢(最优解xbest)将被延续到下一代;

(3)宿主鸟巢的数目n 是固定的，且宿主以一定概率pa发现并丢弃“外来者”或重新筑巢.

其位置更新是通过实施Lévy 飞行来实现的，具体为:

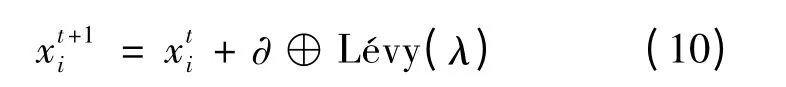
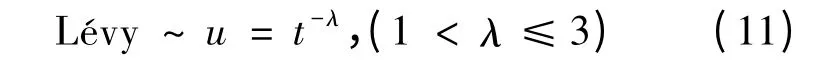
图3 双二极管模型电压－电流特性曲线对比

图4 双二极管模型电压－功率特性曲线对比

3.2 交叉熵方法

交叉熵方法(Cross－entropy Method，CE)［11］是Rubinstein 在研究复杂随机网络中的小概率事件估计问题时提出的一种全局随机优化方法.它是一种蒙特卡洛方法，具有随机性、自适应性和鲁棒性等特性，在组合优化、连续函数优化以及机器学习等方面取得很好的应用［11～12］.CE 的实施步骤为:

Setp2 用引导搜索向全局最优解逼近的精英解集来按下(12)和(13)式更新概率密度函数的参数，产生迭代序列，直至满足终止条件.

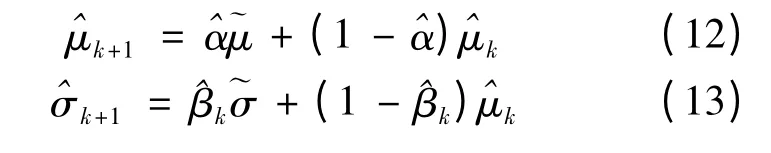
3.3 基于交叉熵改进的布谷鸟搜索

(1)算法原理

本文将交叉熵方法嵌入到布谷鸟搜索中，通过CS 和CE 的协同演化来共同更新种群，以增强种群的多样性，提高算法的全局优化能力.其中CE算子利用共同更新后的种群来刷新自己的抽样概率分布的参数，加快均值和方差的演化速度，这样可以大幅减少抽样样本数，进而降低计算成本，充分发挥自己的全局优化能力，为协同演化提供全局更优的种群;同时CS 算子通过协同演化获得更好的个体，极大地丰富了种群的多样性，从而加快CECS 算法的收敛速度和提高其寻优精度.

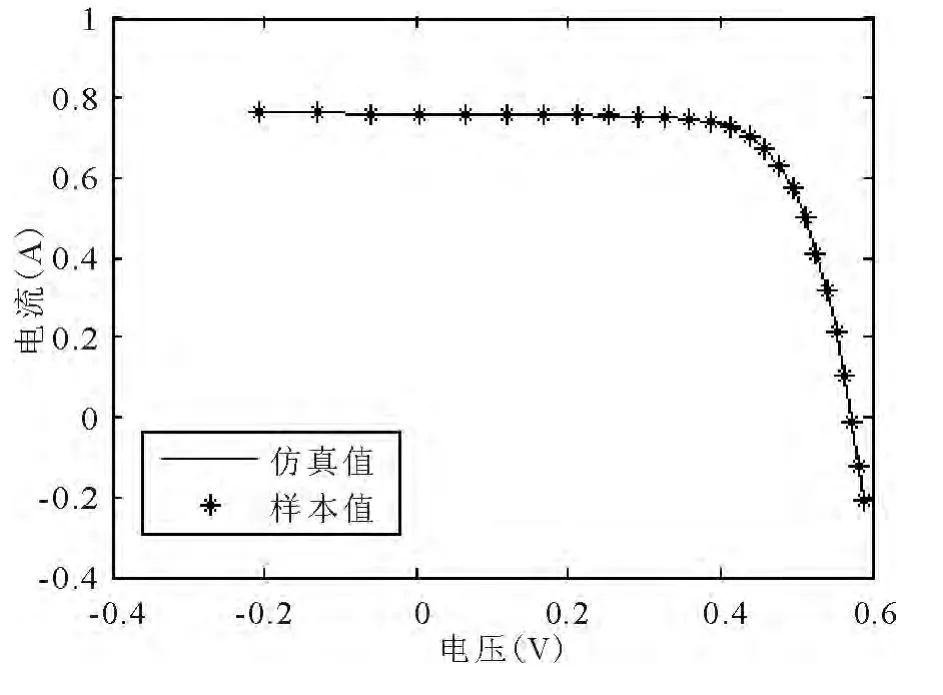
图5 单二极管模型电压－电流特性曲线对比

图6 单二极管模型电压－功率特性曲线对比

(2)算法步骤

CECS 的算法步骤如下:

Step1 确定搜索空间，设置CS 基本参数，初始化概率分布参数;随机生成初始种群并评估.

Step2 检测迭代终止条件1，若不满足，则启动CS 算子，否则迭代结束.

a.利用Lévy 飞行机制，按(10)得到新鸟巢位置并更新.

b.利用发现遗弃机制，更新鸟巢位置.

c.评估鸟巢，更新最优位置和最优适应度值.

Step3 检测迭代终止条件2，若不满足，则启动CE 算子，否则转到Step2.

a.按概率分布参数抽取样本得到CE 优化的种群.

b.启动协同演化，两个种群共同更新、排序，并更新最优位置和最优适应度值.

c.用(12)和(13)式平滑更新，返回到Step3.

Step4 迭代结束，输出最优鸟巢位置(最优解)和最优适应度值(最优值).

4 仿真实验与结果分析

为了测试本文所构建的CECS 算法用来识别光伏电池模型参数时的优化效能，采用文献［5 ～8］所使用的测试案例，并与其实验结果进行对比.CECS 算法的参数设置:鸟巢数目设定为50，CS 的最大迭代次数为40;CE 样本容量和有效样本数分别为120 和30，最大迭代次数为30，迭代停止标准为达到最大迭代次数，对每个测试数据集独立运行30 次，取其平均值.实验硬件环境为Intel(R)Core(TM)i3，CPU M2.27GHz，2GB RAM;软件环境为Windows 7 和Matlab 2012b.

4.1 双二极管模型参数识别与仿真结果

用CECS 算法对双二极管光伏电池模型进行参数识别，得到该模型的7 个参数的最优值和相应的评价函数(RMSE)的值如下表2 所示，并与PS［5］、SA［6］、HS［7］和ABSO［8］等算法的识别结果进行对比，其中最好的RMSE 用粗体标识.

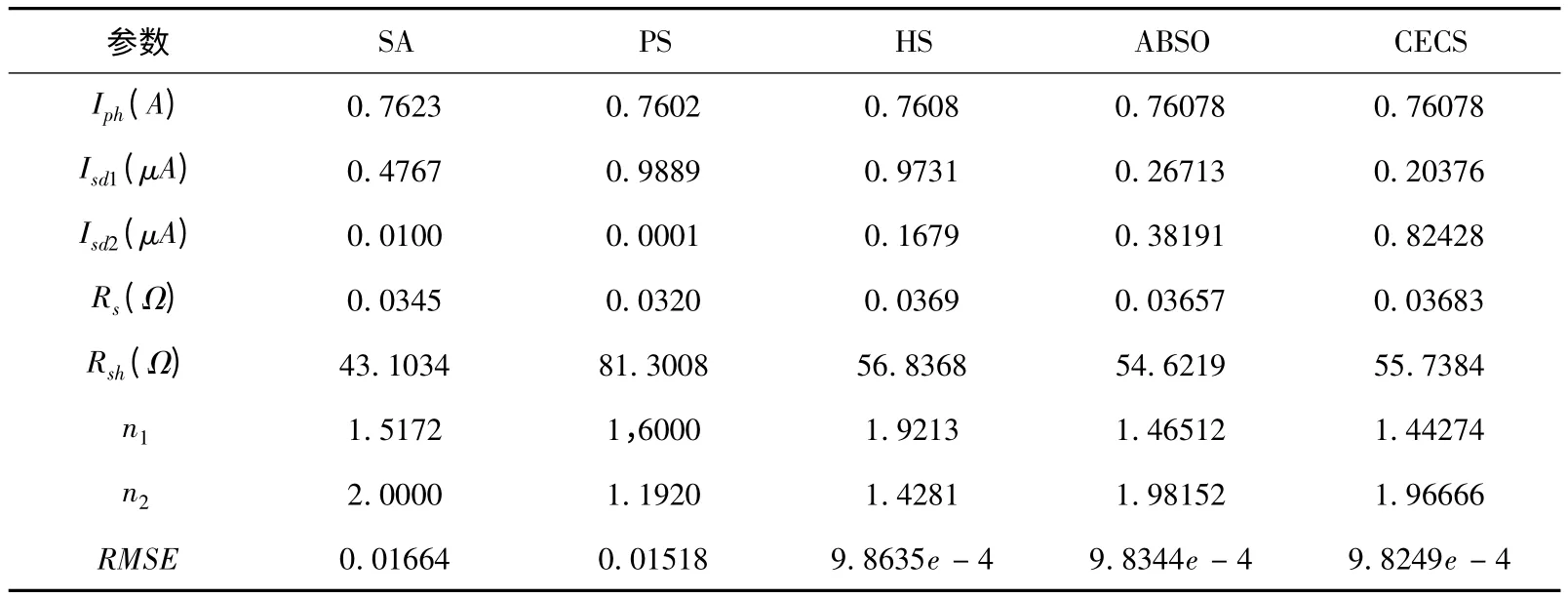
表2 双二极管光伏电池模型参数识别结果与对比

从上表2 可以看出，CECS 算法所获得的模型参数对应的26 个采样点数据的均方根误差(RMSE)最小的，因此该算法所确定的模型参数与系统参数最为接近，是最优参数，其次是ABSO 算法，SA 是四种算法中表现最差的.为了进一步检验所获得模型参数的质量，选用数据集中电压值U(真实值)，借助于牛顿法在Matlab 环境下实现对双二极管光伏电池模型进行仿真进而得到相应的电流值I(仿真值)，如前图3 和图4 分别给出双二极管光伏电池模型的电压－电流特性曲线图和电压－功率特性曲线图.

如前图3 和图4 表明模型仿真曲线与采样数据点十分吻合，更为直观地印证了CECS 算法对该模型参数识别的优异表现和有效性.

4.2 单二极管模型参数识别与仿真结果

如前所述，用CECS 算法对单二极管光伏电池模型进行参数识别，得到该模型的5 个参数的最优值和相应的评价函数(RMSE)的值如下表3 所示.

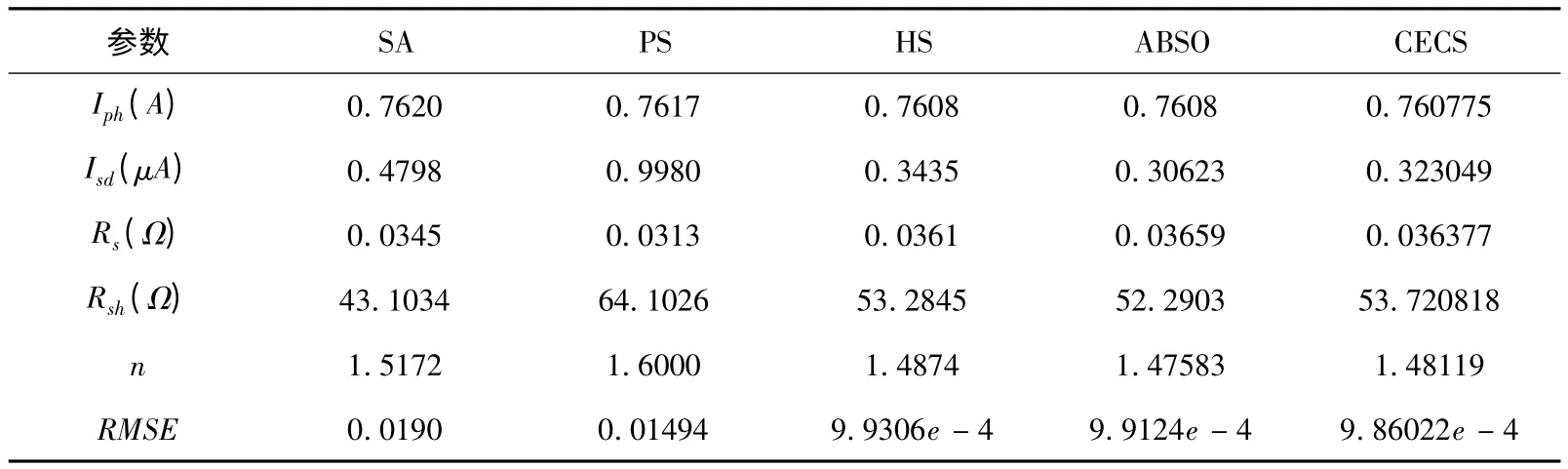
表3 单二极管光伏电池模型参数识别结果与对比

从上表3 可以看出，均方根误差(RMSE)最小 的也是CECS 算法，表明该方法所获得的模型参数是最优的，其次是ABSO 算法和PS 算法，表现最差的是SA.同样，借助牛顿法进行仿真得到电流值I，如前图5 和图6 分别给出单二极管光伏电池模型的电压－电流特性曲线图和电压－功率特性曲线图.

同样，从前图5 和图6 中可以看出单二极管光伏电池模型的仿真特性曲线与采样点数据是高度吻合，充分体现CECS 算法对该单二极管光伏电池模型参数识别的有效性和优异性.

5 结 论

本文将交叉熵全局随机优化方法嵌入到布谷鸟搜索仿生算法中去，采用协同演化技术，实现两种算法的有机融合，进而构建出一种改进的布谷鸟搜索.该算法充分利用协同演化技术实现了交叉熵随机优化方法和布谷鸟搜索的优势互补，克服了布谷鸟搜索迭代后期速收敛速度慢和交叉熵算法需要进行大量抽样的不足，拥有收敛速度快、寻优精度高和全局优化性能好等特质.该算法成功应用于光伏电池模块参数识别这一具有多个局部极值的非线性优化问题，仿真测试和对比结果表明该算法识别精度高、仿真效果好，更能准确刻画实际光伏电池模块系统，对光伏电池模块系统的电气特性刻画和实时控制具有一定的实际意义.

［1］ Cotfas D T，Cotfas P A，Kaplanis S.Methods to Determine the DC Parameters of Solar Cells:A Critical Review［J］.Renewable and Sustainable Energy Reviews，2013，28:588－596.

［2］ Villalva M，Gazoli J，Filho E.Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays［J］.IEEE Transactions on Power Electronics，2009，24(5):1198–1208.

［3］ 傅望，周林，郭珂，等.光伏电池工程用数学模型研究［J］.电工技术学报，2011，26(10):211–216.

［4］ 高金辉，苏军英，李迎迎.太阳电池模型参数求解算法的研究［J］.太阳能学报，2012，33(9):1458–1462.

［5］ AlHajri M，El－Naggar K，AlRashidi M，et al.Optimal Extraction of Solar Cell Parameters Using Pattern Search［J］.Renewable Energy，2012，44(0):238–245.

［6］ El－Naggar K，AlRashidi M，AlHajri M，et al.Simulated Annealing Algorithm for Photovoltaic Parameters Identification［J］.Solar Energy，2012，86(1):266–274.

［7］ Askarzadeh A，Rezazadeh A.Parameter Identification for Solar Cell Models Using Harmony Search－based Algorithms［J］.Solar Energy，2012，86(11):3241–3249.

［8］ Askarzadeh A，Rezazadeh A.Artificial Bee Swarm Optimization Algorithm for Parameters Identification of Solar Cell Models［J］.Applied Energy，2013，102(C):943–949.

［9］ Yang X S，Deb S.Cuckoo Search Via Lévy Flights［C］.Proc.of the 2009 World Congress on Nature＆Biologically Inspired Computing.India:IEEE Computer Press，2009:210–214.

［10］ Moravej Z，Akhlaghi A.A Novel Approach Based on Cuckoo Search for DG Allocation in Distribution Network［J］.International Journal of Electrical Power＆Energy Systems，2013，44(1):672－679.

［11］ Rubinstein R Y，Kroese D P.The Cross－entropy Method:A Unified Approach to Combinatorial Optimization，Monte Carlo Simulation and Machine Learning［M］.New York:Springer－Verlag，2004.

［12］ Kroese D P，Portsky S，Rubinstein R Y.The Cross－entropy Method for Continuous Multi－extremal Optimization［J］.Methodology and Computing in Applied Probability，2006，8(3):383–407.