永磁同步电动机混沌系统的控制研究①

周群利

(芜湖职业技术学院电气工程学院，安徽芜湖241006)

0 引 言

永磁同步电动机在合适的参数以及适宜工作环境下会发生混沌现象［1～2］，这将严重危及电机转动的稳定性，直接影响到系统的运行质量和可靠性［3］.在电机混沌现象的研究中，张波等得到了一个适合分析永磁同步电动机混沌运动的模型［4］，本文针对此混沌模型，采用自适应控制策略研究混沌的控制问题.

1 永磁同步电动机混沌系统的数学模型

采用文献［4］提出的永磁同步电动机混沌运动的数学模型，描述如下:

图1 PMSM 混沌系统的相图

2 永磁同步电动机混沌系统的控制

当系统参数未知时，采用自适应控制方法使永磁同步电动机混沌系统的状态控制到任意一个不稳定平衡点P(x0，y0，z0).设系统状态=(x，y，z)，对式(1)施加控制U，U 为设计的非线性控制器，U=(u1，u2，u3)T，U ∈R3，受控的PMSM混沌系统的状态方程变为:

在平衡点P(x0，y0，z0)处，对(2)式的状态变量进行坐标变换，变换规则为:

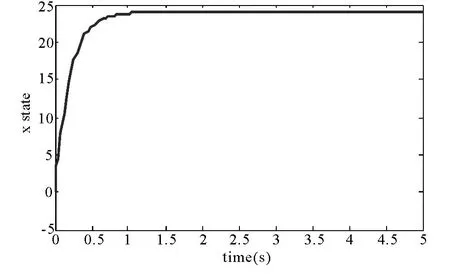
图2 变量x 的状态响应曲线

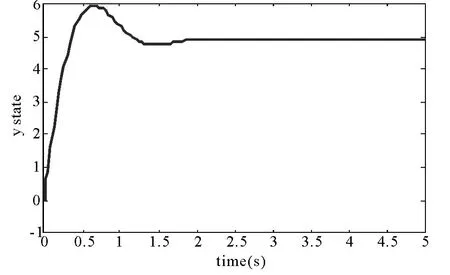
图3 变量y 的状态响应曲线

将(3)式代入(2)式，则受控的PMSM 混沌系统的状态方程变为:

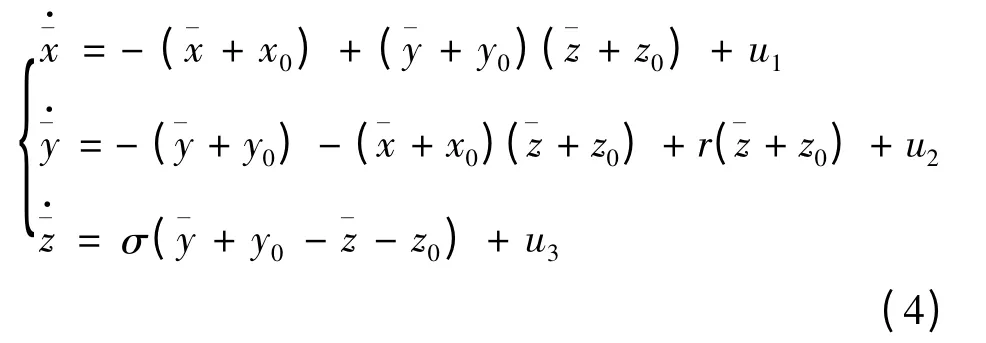
根据坐标变换规则，可以看出:将永磁同步电动机混沌系统的状态控制到不稳定平衡点P(x0，y0，z0)的问题就转化为系统(4)式在坐标原点的镇定问题［6］.

定理 当设计如下控制器

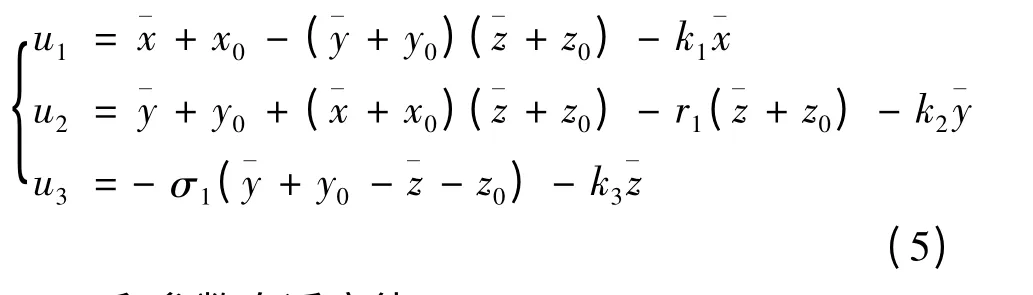
和参数自适应律

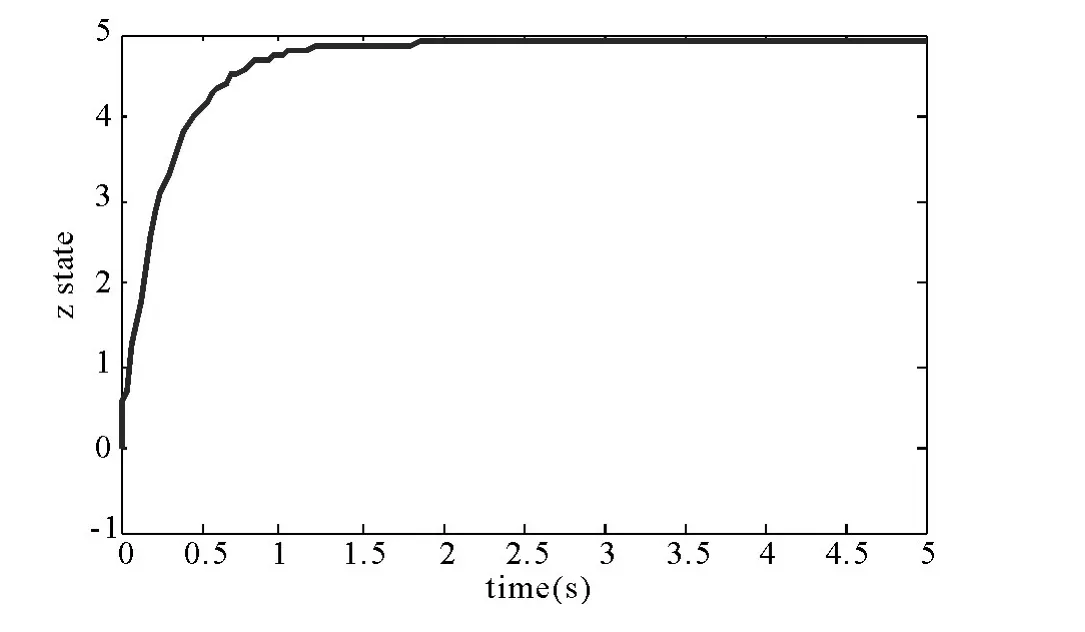
图4 变量z 的状态响应曲线

图5 PMSM 混沌系统控制后的相图

图6 参数r 估计值随时间t 的变化曲线

图7 参数σ 估计值随时间t 的变化曲线

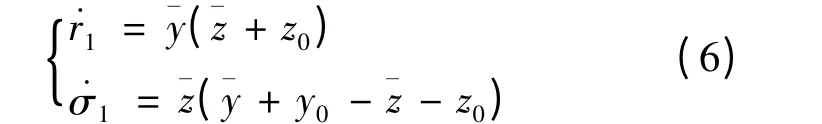
时，受控系统(4)式关于原点渐进稳定，即永磁同步电动机混沌系统被控制到不稳定平衡点P(x0，y0，z0).(5)式中r1，σ1分别为对系统未知参数r，σ 的估计值，k1，k2，k3为反馈增益，均为大于零的数值.

下面来证明上述定理，将(5)式代入(4)式可得:

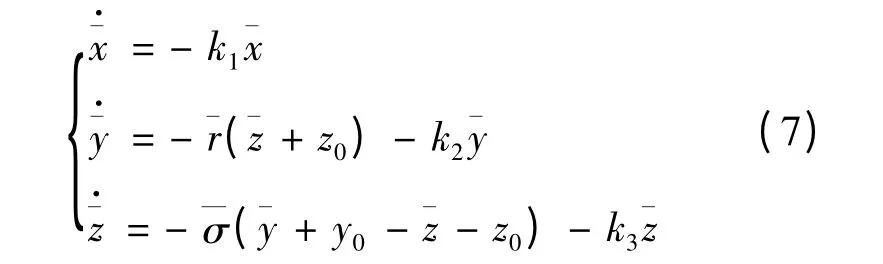
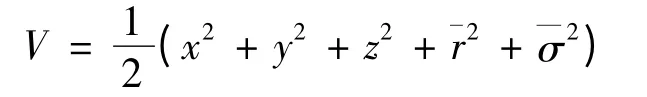
则

因此

3 仿真结果

下面进行仿真，使永磁同步电动机混沌系统的状态控制到任意一个不稳定平衡点，P(x0，y0，z0)，在此以控制到不稳定平衡点P1(24，4.899，4.899)为例，假定“已知”系统参数为σ=2，r=3，为作图方便设参数r 估计值为参数1，参数σ 估计值为参数2，系统状态变量初值(x(0)，y(0)，z(0))=(－0.01，－0.01，－0.01)，系统参数初值r1(0)=1，σ1(0)=1，反馈增益k1=5，k2=5，k3=4.

从图2、图3、图4 可以看出受控的永磁同步电动机混沌系统的状态变量在很短时间内稳定地收敛于不稳定平衡点P1(24，4.899，4.899);图5 为系统施加控制后的相轨迹图;图6、图7 分别为系统参数r，σ 估计值随时间t 的变化曲线，经过很短的时间，系统未知参数的估计值稳定地收敛于一个固定的常数.

4 结 论

研究了永磁同步电动机系统中存在的混沌现象，并采用自适应控制策略对此现象进行控制，使混沌系统的状态在很短时间内镇定到任意一个不稳定平衡点，从而消除了混沌现象.通过数值仿真，可以发现该方法对系统参数未知或不确定系统的混沌控制还是非常有效的.

［1］ 韦笃取，张波，丘东元M 等.基于LaSalle 不变集定理自适应控制永磁同步电动机的混沌运动［J］.物理学报，2009，58(9):6026－6029.

［2］ 薛薇，郭彦岭，陈增强.永磁同步电机的混沌分析及其电路实现［J］.物理学报，2009，58(12):8146－8151.

［3］ 王鹍，史庆武，黄跃娟.永磁同步电动机的混沌控制［J］.林业机械与木工设备，2009，37(5):24－25.

［4］ 张波，李忠，毛宗源，等.电机传动系统的不规则运动和混沌现象初探［J］.中国电机工程学报，2001，21(7):40－45.

［5］ 周群利.输入－状态线性化控制永磁同步电动机混沌系统［J］.西昌学院学报，2014，28(2):55－57.

［6］ 崔俊峰，祝泽华.一个新自治混沌系统的混沌控制［J］.甘肃高师学报，2012，17(2):6－8.