高层建筑物沉降监测数据处理方法研究①

郑 丽

(宿州学院环境与测绘工程学院，安徽 宿州234000)

0 引 言

随着科学技术的迅猛发展和我国现代化进程的不断加快，城市各类高层建筑物越来越普遍.由于建筑物的增高、荷载的增加，在地基基础和上部结构的共同作用下，建筑物将发生不均匀沉降，轻者将使建筑物产生倾斜或裂缝，影响正常使用，当变形值超过一定限度时，会影响建筑物本身的安全以及人民生命财产的安全［1～2］.因此，在建筑物施工和运营期间，有必要设计一个合理、可行的沉降监测方案，对它们进行定期监测，根据已测数据进行合理地统计分析和研究，对其进行相应预测预报是非常必要的［3］.

目前，建筑物变形预测应用比较多的方法主要包括:回归分析、灰色预测、神经网络等，很多学者对建筑物变形监测预测工作展开研究，王旭华等［4］应用指数平滑法对建筑物的变形进行预测，通过某大楼一沉降监测点45 期实测数据，对比分析了指数平滑法及改进指数平滑法预测值，结果表明改进的平滑法克服了原方法的误差累积的缺点，取得较好预测结果.李德江等［5］通过工程实例证明基于支持向量机的建筑物沉降预测模型可行性，并将预测结果与BP 神经网络的预测结果相比，借助绝度误差和相对误差测算，得出支持向量机建筑物沉降预测模型更好的结论.谢波［6］针对建筑物变形监测的动态特性，阐述了卡尔曼滤波和附加衰减因子自适应卡尔曼滤波的算法，通过工程实例相关观测数据建立自适应卡尔曼滤波法建筑物动态模型，表明其在建筑物变形监测中的应用前景.邹广黔［7］运用传统灰色GM(1，1)模型和动态GM(1，1)模型分别建立高层建筑物变形监测数据模型，研究结果表明动态模型更适合于中长期变形监测数据处理.为此，笔者应用三次指数平滑模型，探索建筑物沉降预报工作，可为高层建筑物监测预报工作提供一定的借鉴和参考.

1 三次指数平滑模型

若一个时间序列的未来值被某一个数学函数严格确定，则称该时间序列为确定性的.确定性时间序列分析模型主要包括:移动平均模型、二次滑动平均模型、指数平滑模型、二次指数平滑模型和三次指数平滑模型［8］.

若时间序列数据点的分布出现曲率，则应使用三次指数平滑(Triple Exponential Smoothing)模型进行预测，它是建立在二次指数平滑模型的基础上，得到了二次指数平滑模型的平滑数据后，再进行一次平滑，平滑公式如下:

有了三次指数平滑模型，可得到三次指数平滑的预测公式为:

其中:T 为预测周期，根据最小二乘法确定参数at，bt，ct按下述公式计算:

2 工程概况

沉降监测的方法是通过布设基准点和沉降观测点，采用周期观测来获取建筑物沉降数据，并对沉降数据进行分析，及时发现建筑物的沉降情况，以便采取科学措施，确保高层建筑物施工的安全.本工程为建设高层建筑，主要由17 个单体工程组成，其中2 栋为29 层框架结构，在建设过程中，参照建筑物设计总平面图、建筑设计图及《建筑物变形监测规范(2007)》，在建筑物主要轴线布设六个变形监测点，具体点位布设情况如图1 所示.这些变形观测点埋设于室内地坪上方20 ～30cm 左右，从2012 年的4 月至12 月进行了12 期的变形观测，从而了解建筑物的沉降变化情况.

在沉降观测中，2 号沉降点的沉降值最大为6.6 mm，沉降值最小为0mm，累计沉降量41.5mm，平均沉降值3.46mm ＜200mm 符合高层建筑物的沉降的允许范围(《建筑地基基础设计规范》中表5.3.4 建筑物的地基允许变形值中规定体型简单的高层建筑物基础的平均沉降量200mm)，说明该点的沉降量均属正常，暂未出现异常变化，所有观测结果均符合国家的相关规范(《建筑地基基础设计规范》、《建筑变形测量规范》和《建筑物沉降观测方法》)的要求.

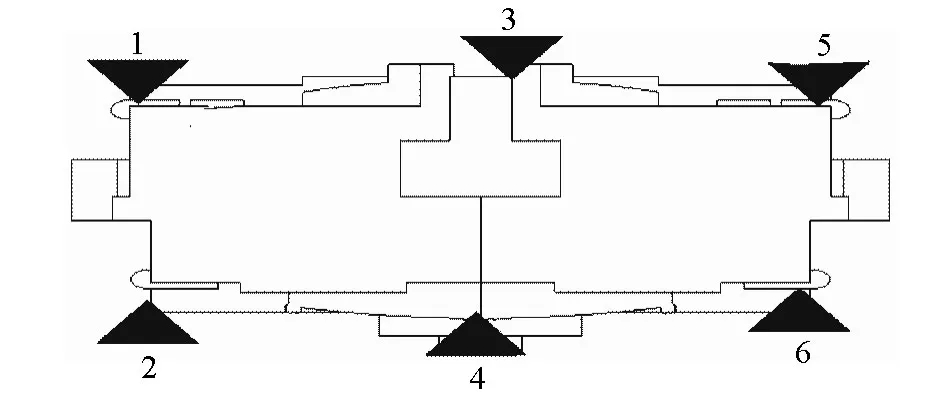
图1 沉降监测点分布图

本文以监测点2 的沉降值为样本数据，用于计算模型参数，建立三次指数平滑模型，进行预测，以与实际沉降量作比较.由于建筑物沉降影响因素较为复杂，观测数据起伏较大，规律性不明显.基于均方拟合误差最小的原则，运用试算法，经多次计算，选取较好的a 值为0.23，此时均方误差为0.2533，指数平滑值分别为at=6.7171，bt=0.5596，ct=－0.0047，因而建立三次指数平滑预测模型为:

^yt+T=6.7171+0.5596T－0.0047T2(6)

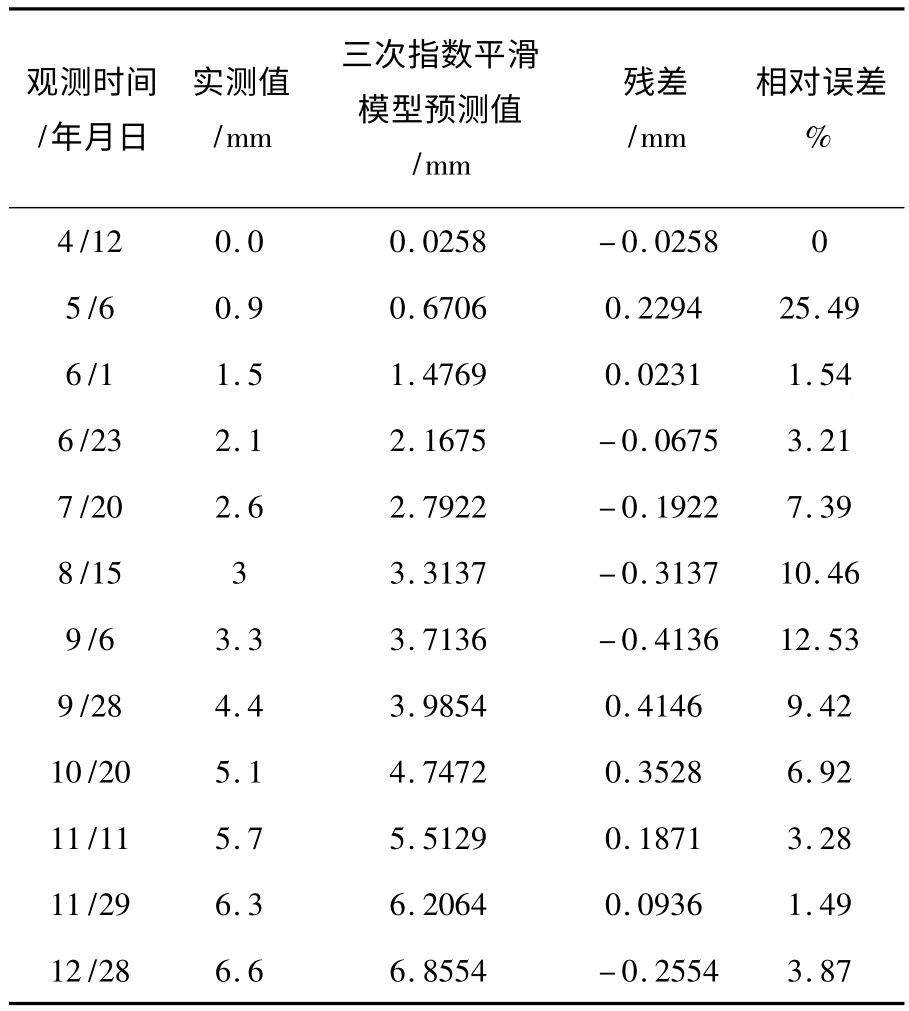
表1 2 号点沉降观测值与预测值一览表

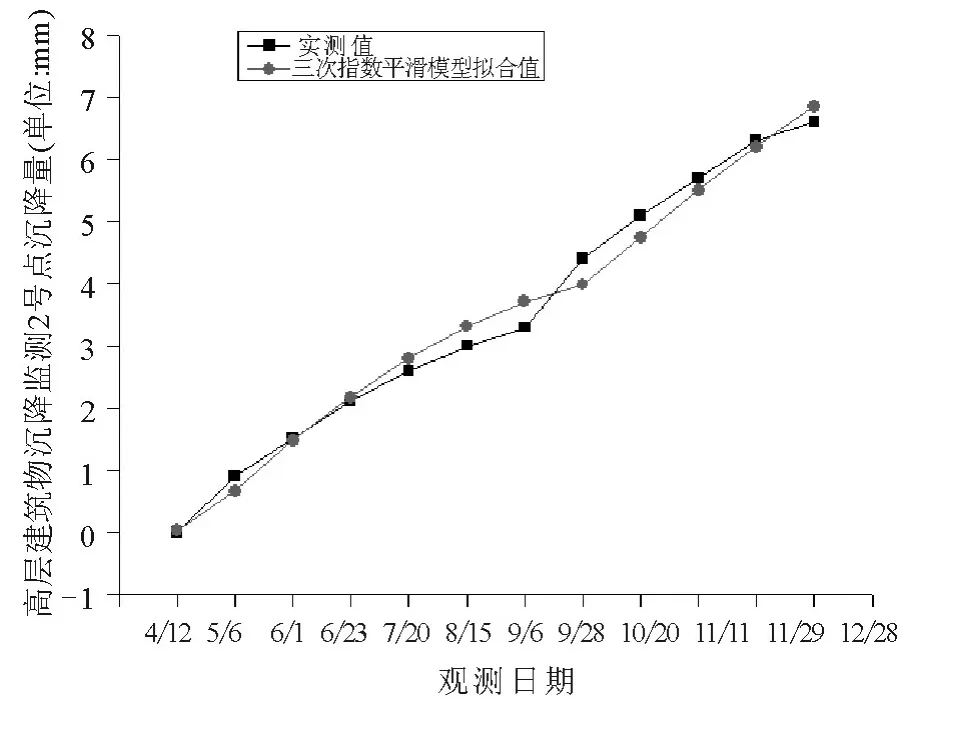
图2 2 号点沉降量实测值与拟合值变化趋势图

从表1 中可以看出:所建立三次指数平滑模型残差绝对值均小于0.5mm，相对误差最小为0，最大为25.49%，平均相对误差为7.13%，根据表1所得数据绘制2 号点沉降量实测值与拟合值变化趋势图2.从图2 中可以发现:2 号点4 ～12 月12期观测数据参与建立三次指数平滑模型条件下，模型预测变形量与实际变形量，相差较小，说明该三次指数平滑模型基本可靠，对于确保高层建筑物施工和运营管理有重要意义.

3 结 论

高层建筑物沉降监测是非常有必要的.在施工期间，结合具体工程实况，根据所增加层数和荷载情况逐步进行沉降观测.本文基于高层建筑物沉降监测中2 号监测点12 期实测数据建立三次指数平滑模型，以掌握、监控建筑物的沉降情况，分析是否正常，若有异常情况发生，需及时分析采取相应的措施，以保证建筑物的施工安全.通过实证分析得出以下结论:

(1)根据时间－沉降－曲线图可以判断出，原始沉降量具有趋势性，选择三次指数平滑模型.高层建筑物沉降监测数据处理方法很多，将三次指数平滑模型应用于高层建筑物沉降监测，具有方法简便，容易操作，预测精度高等特点，及时反馈某些点的动态沉降量，以判断沉降变化量是否出现异常，以便及时采取相关措施，避免安全事故的发生.

(2)通过工程实例可知高层建筑物沉降监测是一项长时间不间断的测量工作，应尽量避免使用三次指数平滑模型进行中长期变形监测预报工作，且要根据实测监测数据对所建模型实时更新，取得较好预测效果.

此外，工程沉降是由地基、基础和上部结构以及降水共同作用的结果，进行建筑物沉降监测仅仅是其中一个方面，若观测期内，沉降量若超过一定的限度，就会影响物的正常使用和安全.这就要求从建筑物的沉降程度映射到整个地区的沉降趋势，引起足够的重视［9］，确保建筑物施工和运营的安全.

［1］ 丁宁，孙英君，崔健，等.高层建筑物变形监测数据处理与分析［J］.测绘科学，2011，36(5):93－94.

［2］ 熊俊楠，王泽根等.高层建筑物变形监测数据处理方法研究及工程应用［J］.测绘科学，2010，35 增刊:69－71.

［3］ 陈伟清.灰色预测在建筑物沉降变形分析中的应用［J］.测绘科学，2005，30(5):43－45.

［4］ 王旭华，陈雄，赵德深.指数平滑法在建筑物变形预测中的应用［J］.测绘通报，2004，(3):28－30.

［5］ 李德江，花向红，李涛，朱成林.基于支持向量机的建筑物沉降预测模型研究［J］.测绘工程，2009，18(3):29－31.

［6］ 谢波.卡尔曼滤波在建筑物变形监测中的应用［J］.长春工程学院学报(自然科学版)，2013，14(3):8－10.

［7］ 邹广黔.高层建筑物形变监测中动态灰色理论模型的应用［J］.测绘与空间地理信息，2010，33(1):197－200.

［8］ 任永泰.经济数学方法与模型［M］.北京:中国农业出版社，2008:109－110.

［9］ 温宇斌.建筑物沉降监测的实践及探讨［J］.测绘通报，2002，(11):37－39.