后注浆灌注桩桩端竖向承载力可靠性分析①

张 杰，朱晓丽

(济源职业技术学院，河南 济源459000)

0 引 言

随着城市建设的不断加快，桩基础作为高层建筑的主要基础形式，后注浆钻孔灌注桩以其能提高承载力，减少沉降而被广泛采用.桩基础作为主要承受竖向荷载的构建，其承载力的研究一直备受关注.因此对桩基承载力估算方法的可靠性一直是岩土工程中一项重要的研究课题.

在进行可靠度研究时，常采用的计算方法有一次二阶矩法，JC 法，蒙特卡洛法，有限元法等.然而一次二阶矩法仅适用于正态分布的随机变量，适用范围较小，蒙特卡洛法则计算过程复杂，因而JC 法更适合于工程实际设计中.

国内对桩基可靠性研究开始于八十年代后期.李强［1］采用蒙特卡洛法研究抗滑桩桩侧岩土体受压的三个极限状态方程的可靠指标，并根据结果确定了目标可靠指标，最后提出分项系数设计方法.吴鹏［2］对超长超大群桩基础进行了沉降可靠度研究，并采用蒙特卡洛法计算可靠度.李典庆，鄢丽丽［3］考虑桩底沉渣这一缺陷，研究单桩灌注桩的可靠度指标.推导了此情况下，桩承载力的偏差系数以及变异系数的公式.李典庆［4］结合线性回归的理论改进了失效准则偏差系数，消除了偏差系数与随机变量之间的相关性.徐志军［5］对群桩承载力可靠度进行研究，并提出了基桩可靠度的优化设计方法，并详细叙述了桩基在竖向荷载作用下可靠度的优化设计过程.

在进行可靠度研究时大多关注理论方法的研究，对于各种类型的桩基可靠度研究也只是提出了一种计算方法，并未对其中的参数进行深入分析.本文以后注浆钻孔灌注桩的桩端竖向承载力为例，研究随机变量数，极限状态方程对可靠度指标的影响，并进行了参数敏感性分析.

1 可靠度分析方法的基本理论

本文主要针对实际工程设计问题，考虑到JC法原理简单收敛速度较快，故本文采用的可靠度研究方法为JC 法.图1 为JC 法的流程图.

JC 法需要通过不断迭代，得到新的验算点，当前后两次计算得到的可靠度指标差值满足精度要求，则结束迭代.

2 桩端位于砂土层中的桩端后注浆灌注桩竖向抗压承载力可靠度

2.1 基本原理

根据建筑桩基技术规范规定后注浆单桩极限承载力的标准值按式(3)估算.

图1 JC 法流程图

式中:QSK为非竖向增强段总极限侧阻力的标准值;Qgsk为竖向增强段总极限侧阻力的标准值;Qgpk为总极限端阻力的标准值;u 为桩身的周长;lj为非竖向增强段第j 层土层的厚度;lgi为竖向增强段内第i 层土层的厚度:本文算例为桩端复式注浆时，根据规范竖向增强段取为桩端以上12m，其中重叠部分应扣除;qsik，qsjk，qpk为分别为竖向增强段第i土层初始极限侧阻力的标准值、非竖向增强段第j土层初始极限侧阻力的标准值及初始极限端阻力的标准值;βsi，βp为分别为后注浆侧阻力、端阻力的增强系数.规范要求桩径大于800mm 的桩，要进行侧阻和端阻尺寸效应修正.

2.2 算 例

选取上海某广场后注浆钻孔灌注桩［6］，桩端位于砂土层中，桩径850mm，桩长70m，桩底绝对标高－67.10m，桩顶绝对标高2.90m.场址内地基土在勘探深度内分为12 个工程地质层，本文将土层简化为3 层，土层如图2 所示.在进行承载力可靠度分析时，构造极限状态方程:

图2 土层情况

根据式(3)，增强段长度为12m，全部处于第三层土中.参数选取参照建筑桩基技术规范(JGJ 94－2008)，算例中桩径＞800mm，βsi，βp需进行尺寸效应修正.处于黏土层中的桩段βsi的修正系数为0.988，砂土层中的桩段βsi的修正系数为0.980;桩端位于砂土层中，则βp的修正系数为0.980.参数选取结果如表2 所示.

表1 参数选取

qsjk 61 βsi 1.7640(修正后结果)βp 2.5480(修正后结果)

2.3 随机变量数量对可靠度的影响

一般而言构造的极限状态方程通常比较复杂，因而变量数量的选取是在进行可靠度计算时需要注意的一个问题，变量选取过少可能会造成计算结果的误差较大，变量选取过多则会造成计算时间过长.本文针对算例选取了2 个变量、4 个变量及6个变量三种选择方式，进行了可靠度计算.变量参数的选择如表2 所示，由于此算例仅作算例研究，故而均值按建筑桩基技术规范建议值选取.

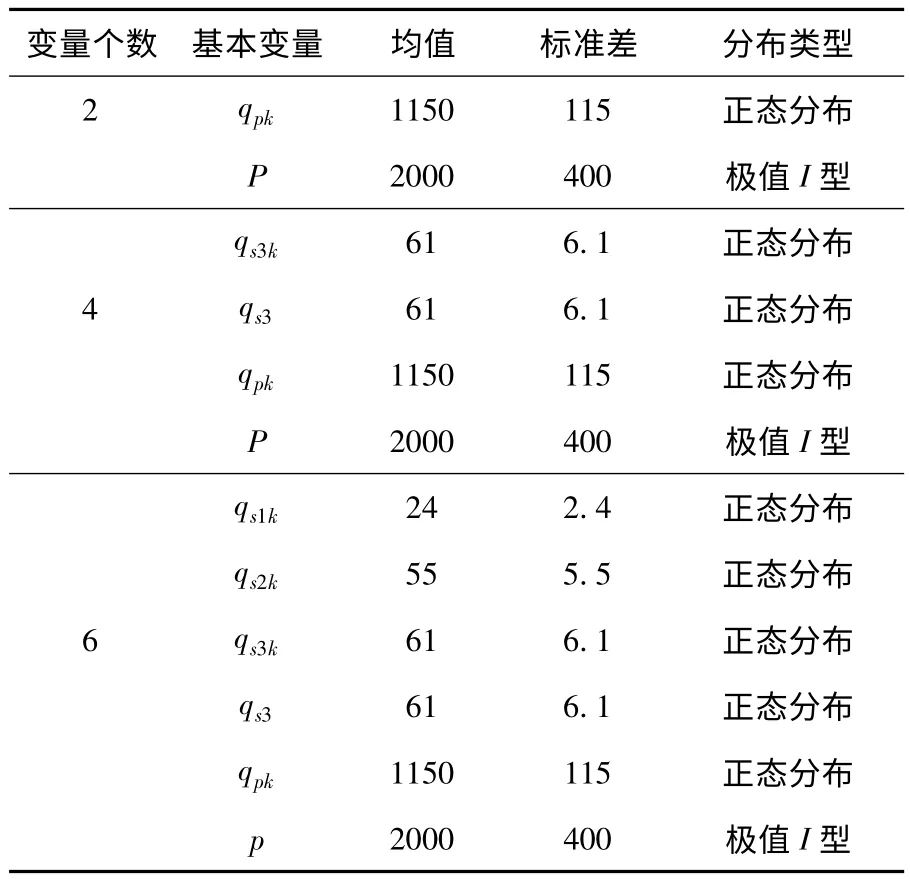
表2 变量参数表

考虑到JC 法需要连续迭代求得可靠度指标，本文编写了matlab 程序，用于解决JC 法计算结构可靠度问题.本程序通过单独的M 文件以方便用户改写极限状态方程.为了实现选取不同基本变量计算可靠度指标β，本文编写的程序适用于1 ～6个基本变量的计算，随机变量有正态分布、对数正态分布及极值I 型分布三种类型可供选择.在主界面上通过读取用户输入的变量数量调用相应的子程序进行可靠指标的计算.2 个随机变量的程序计算结果如下图所示.三种随机变量选取计算得到的可靠度指标如表3 所示.

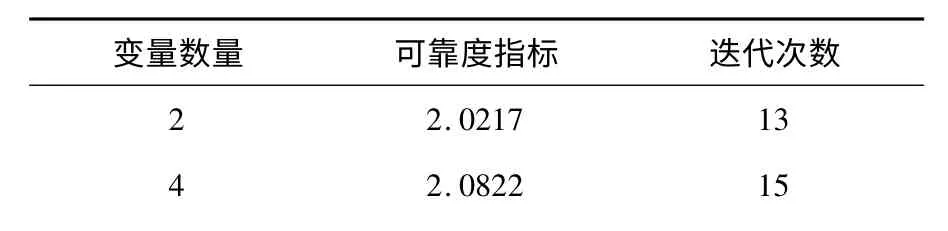
表3 计算结果

从上表研究可以发现，随着变量数量的增加，可靠度指标增大了，同时迭代次数也增加了.变量数增加了2 倍，可靠度指标提升了10%，迭代次数增加了38.5%.对于复杂的实际工程来说，可能因为变量数的增加造成计算工作量的增加，但计算得到的可靠度指标变化不大，这样一来确定合适的随机变量数量是保证可靠度指标计算结果精度以及计算过程经济的首要条件.

图3 程序界面及计算结果

2.4 极限状态方程对可靠度的影响

在进行可靠度计算时，极限状态方程会随着所选的随机变量的不同而变化.同样以上海某广场后注浆钻孔灌注桩为例，随机变量数为4，选择3 组不同的随机变量进行研究，变量参数的选择如表4所示.

表4 变量参数表

表5 计算结果

通过比较三种组合的计算结果发现，三组极限状态方程不同，迭代次数变化不大，但得到的可靠度指标有一定偏差，以第I 组为基准比较，第II 组的可靠度指标减少了1.6%，第III 组的可靠度指标降低了1.5%.

因此不同的极限状态方程对可靠度的计算结果影响较小，可以根据实际工程上掌握的数据资料，选择合适的随机变量进行可靠度指标的计算.

2.5 参数敏感性分析

可靠度指标的计算是基于大量的数据进行的，各个随机变量的均值和标准差也是通过对大量数据的分析得到的，并不是精确取值，存在一定误差.本文针对实例进行了参数敏感性分析，研究各个随机变量的均值及标准差的取值对计算可靠度指标的影响程度.

以6 个随机变量为例，每个变量确定3 个均值，正态分布随机变量的标准差取为均值的0.1，变量参数的选择如表6 所示.其中粉质粘土层选定软塑、可塑、硬可塑三种，粉砂层选定稍密、中密、密实三种，6 个随机变形分别对这六种土层情况取平均值，确定标准差.

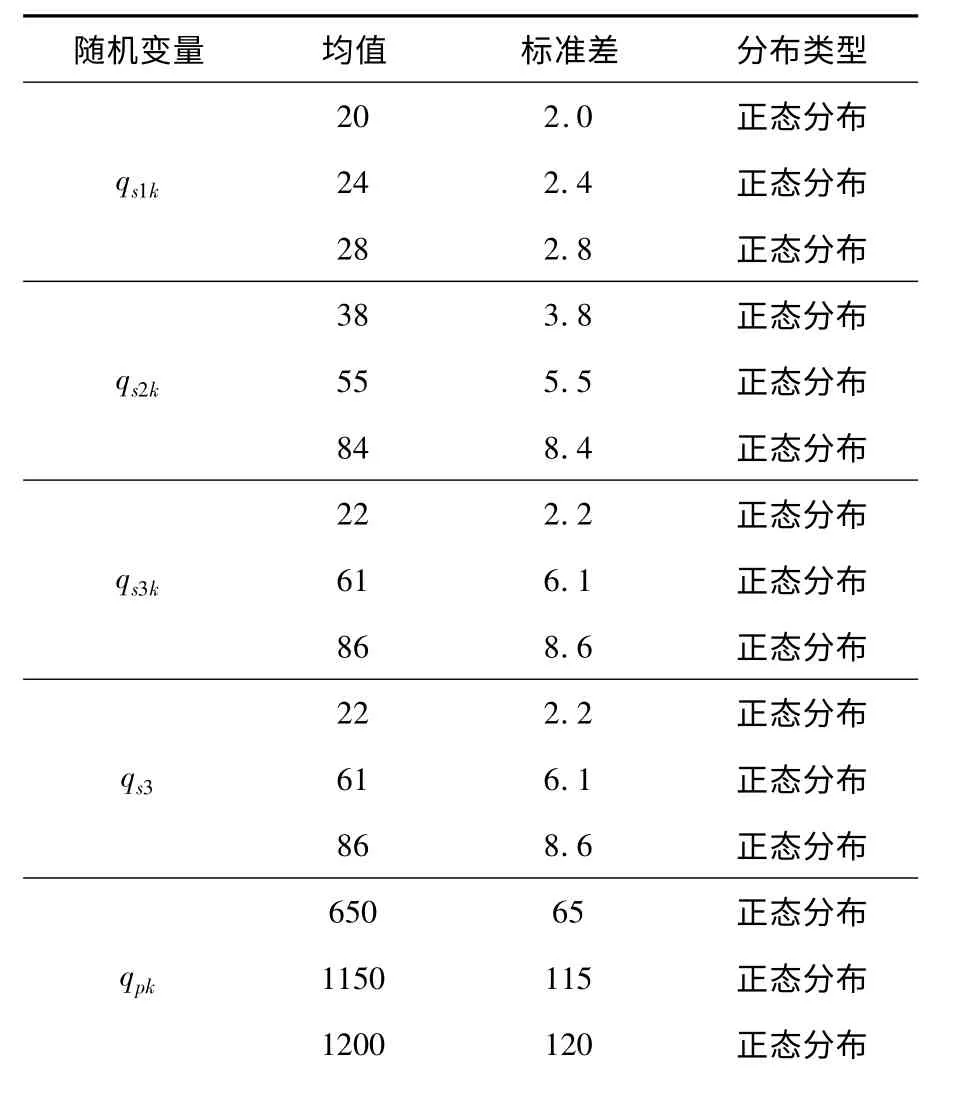
随机变量 均值 标准差 分布类型20 2.0正态分布qs1k 24 2.4 正态分布28 2.8 正态分布38 3.8正态分布qs2k 55 5.5 正态分布84 8.4 正态分布22 2.2正态分布qs3k 61 6.1 正态分布86 8.6 正态分布22 2.2正态分布qs3 61 6.1 正态分布86 8.6 正态分布650 65正态分布qpk 1150 115 正态分布1200 120 正态分布

1000 200 极值I型p 2000 400 极值I 型4000 800 极值I型

计算时，除作为研究对象的随机变量按表6 改变平均值及标准差外，其余随机变量的取值如表2中变量数为6 的工况取值.计算结果如表7 所示.表中变化百分比以表2 中6 个随机变量的可靠度指标计算结果为标准，分析各随机变量选取不同均值及标准差计算得到的可靠度指标相对于标准情况下计算的可靠度指标的偏差.总体变化率则是可靠度指标变化量与均值变化量的比值，研究可靠度指标随均值增加的变化趋势.

图4 均值－可靠度指标曲线图

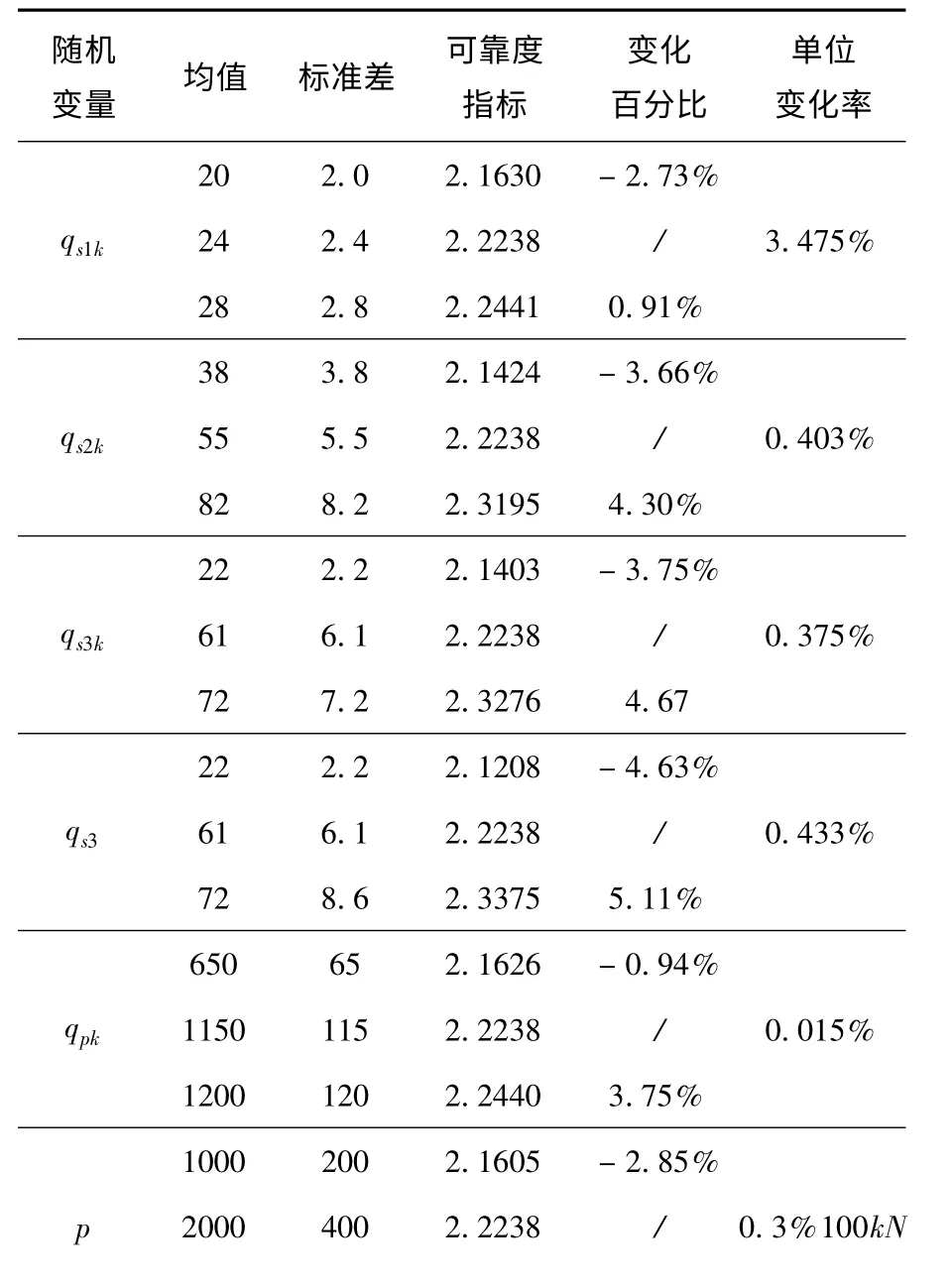
表7 变量参数表

4000 800 2.2447 3.79%

通过对表7 中数据分析得到，在这6 个随机变量中，qs3对可靠度的影响最大，对三种不同性质的土体取参数，三者之间的误差为4.63%，5.11%.若对土性判断存在误差，而导致参数选取偏差较大，会对计算得到的可靠度指标产生较大影响.6个随机变量对可靠度指标影响程度由大到小排序依次为:qs3，qs3k，qs2k，P，qpk，qs1k.由于实例中第一层土为淤泥质粘土，在确定qs1k时变化范围很小，并不会产生过大的偏差，故而对可靠度指标的影响较小.

从具体取值方面来看，在对前5 个随机变量根据规范取均值时，均值选取往往是根据经验在一定范围内确定，选择结果与实际情况偏差的大小将直接影响到可靠度指标的精度，因此研究可靠度指标随均值增加的变化趋势十分重要.从单位变化率中可以看到qs1k的取值对可靠度指标计算结果影响最大，均值每增加1，可靠度指标提升3.475%.qpk对计算结果影响最小，均值每增加1，可靠度指标提升0.015%.其中P 基数较大，在选取时并不会以1kN 为单位进行调整，考虑到此参数的特殊性，选取100kN 为单位，得到单位变化率为0.3%/100kN.6 个随机变量单位变化量对可靠度指标影响程度由大到小排序依次为:qs1k，qs3，qs2k，qs3k，P，qpk.

针对qs2k，qs3k，qs3这三个参数进行细致研究，分析可靠度指标随均值的变化趋势，结果如图4 所示.

从图4 中可以发现，三个条曲线的变化规律基本相同，随着随机变量的增加，可靠度指标也不断增加，并且在起始端及结束端变化较缓慢，中间段变化较大.比较三条曲线的变化趋势，qs3曲线斜率较大，故而其单位变化量对可靠度指标的影响也较大.

3 结 论

随着随机变量数量的增加，可靠度指标增加，且迭代次数也增加.变量数增加了2 倍，可靠度指标提升了10%，迭代次数增加了38.5%.

不同的极限状态方程对可靠度的计算结果影响较小，可以根据实际工程上掌握的数据资料，选择合适的随机变量进行可靠度指标的计算.

在不同土性情况下，各随机变量对可靠度指标的影响qs3最大，其次是qs3k，qs1k最小.在确定土性后具体取值时，各随机变量的单位变化对可靠度指标的影响qs1k最大，其次为qs3，qpk最小.并且可靠度指标随着qs2k，qs3k，qs3的均值增大而增大，两端增加较缓，中间段增加明显.

［1］ 李强.抗滑桩可靠度研究［D］.四川:西南交通大学，2006.

［2］ 吴鹏.基于刚性承台群桩沉降的可靠度研究［J］.岩土力学，2007，28(8):1744－1748.

［3］ 李典庆，鄢丽丽.考虑桩底沉渣的灌注桩可靠度分析方法［J］.岩土力学，2008，29(1):155－160.

［4］ 李典庆.基桩可靠度分析的统计相关性评价方法［J］.岩土力学，2008，29(3):633－638.

［5］ 徐志军.基桩承载力的可靠度分析及可靠度优化设计研究［D］.武汉:华中科技大学，2012.

［6］ 沈晓梅，高飞.软土地区大直径超长后注浆钻孔灌注桩竖向承载力的试验研究［J］.建筑结构，2006，36(4):34－36.