钻孔法检测大型钢结构工作应力的研究①

李 伟，王文欣，李林安，宋 威

(1.天津市市政工程设计研究院，天津300051;2.天津大学，天津300072;3.铁道第三勘察设计院集团有限公司，天津300143)

0 引 言

随着经济的发展，我国在建和筹建的大型钢结构工程越来越多，且其结构越发复杂，它们的安全性也越来越受到关注和重视.国内外大型钢结构出现的安全事故并不罕见，对使用中的钢结构工程进行安全性评估的方法必然会受到越来越多的关注.对于使用中的钢结构建筑来说，构件的工作应力是一个极其重要的参数.设计失误、边界条件变化以及其他诸多不可预见的因素，都会导致构件实际工作应力与设计值有较大偏差，因此对构建的工作应力进行应力状态检测就显得十分必要［1～3］

本文对钻孔法在大型钢结构建筑工作应力检测中的应用方法进行了研究，通过有限元计算对钻孔法理论中的应变释放系数A、B 进行了修正，提出了能够修正钻孔温度效应和径向挤压等因素引起的附加应变的工作应力测试与计算方法，使钻孔法更好的适用于大型钢结构工作应力的检测.运用本文阐述的方法，对天津某大型钢结构建筑工作应力进行了检测，并得到了良好的测试结果.

1 钻孔法检测钢结构工作应力基本原理

1.1 基本物理模型

对于双向受力梁，其初始应力状态如图1(a)所示，在某一位置钻一小孔后应力状态如图1(b)，由于局部应力的释放，会在小孔周围产生相应的应变［1］.

图1 基本物理模型

对于一个未知应力的状态的钢构件，在构件表面钻一个半径为r 深度为h 的小孔，小孔周围的应变场会发生变化，释放的径向正应变εr 是关于构件主应力σ1，σ2和测点相对小孔位置的函数.对于图2 所示平面应力问题及相应的贴片方法，其释放应变计算公式为［4，5］:

应变释放系数A，B 理论计算公式为:

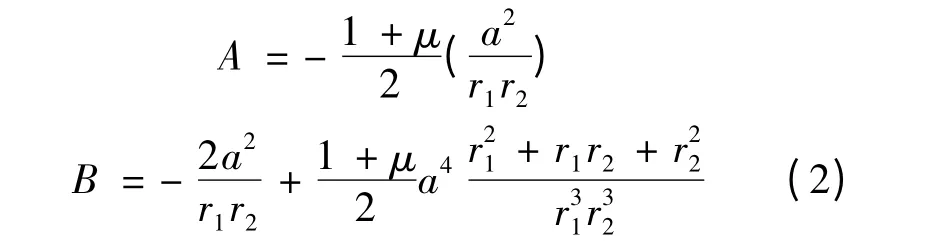
其中:εr为钻孔后释放的应变;σ1，σ2为贴片处构件主应力;α 为εr与主应力方向的夹角;E 为待测构件材料的弹性模量，r1，r2，r3分别为钻孔圆心到应变计内侧、中心及外侧的距离.

图2 应变释放测试原理

1.2 构件工作应力测试基本方法

由上文可知，只要检测出钻孔前、后小孔周围应变的相对变化就可以得出构件应力场分布［4，5］.在此，采用如图3 所示电阻应变片粘贴的方法来测试钻孔引起的应变释放的大小.假设三个应变片与主应力的夹角分别为α0=β，α120=β+120°，α240=β+240°.把这三个角度测得的数据均带入式(1)可得:

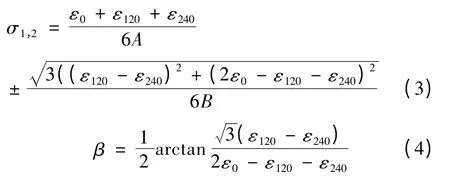
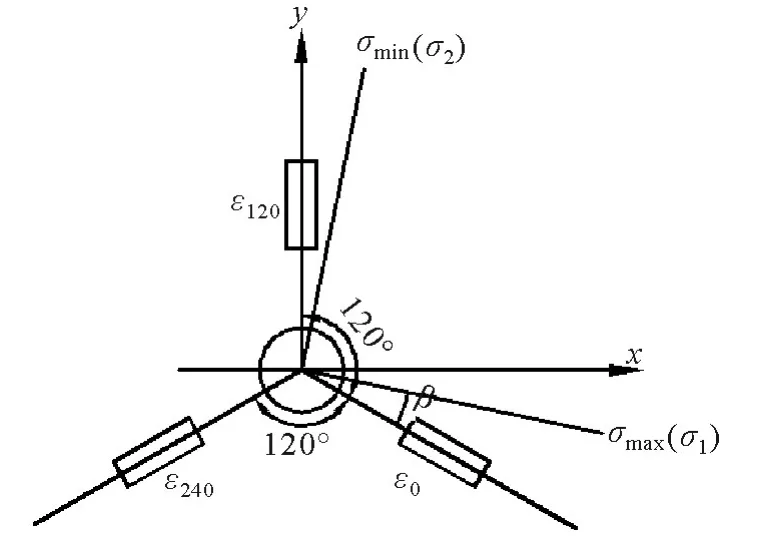
图3 钻孔法测试中应变片粘贴方法

1.3 应变释放系数的有限元修正

按照上文1.1 中提及的模型，式(2)中的应变释放系数可以采用有限元方法对其过程进行模拟［6，7］，首先，建立一个单向受拉完整构件模型，取贴片处所有单元应变均值作为钻孔前应变值.然后建立相同受力状态下的含孔模型，取相同位置单元应变均值作为钻孔后的应变，钻孔后与之前应变值的差即为释放应变值.考虑到模型的对称性，此处采用1/4 模型来计算［6］，从而提高其计算精度.有限元计算模型如图4 所示.

对于一个按图5 所示方法贴片的单向受拉构件，假设σ1=σ，σ2=0，由式(1)可知:

图4 有限元计算网格划分方式

图5 单向受拉梁应变花布置

经过计算可得出

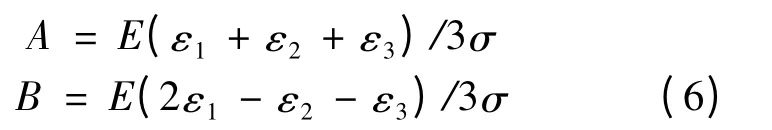
其中:ε1，ε2和ε3即为钻孔后与钻孔前有限元模型中贴片位置应变值的差.

以本文测试所用应变花为例，材料弹性模量E=2.12×1011Pa，泊松比υ=0.278，拉应力σ=100MPa.孔半径a=0.75mm，孔深h=2mm;孔心到应变计内沿、形心及外沿距离分别为r1=1.5mm，r=2.75mm，r2=4mm，应变计宽度l =2mm.把通过有限元计算得出的贴片位置释放应变带入式(6)可得出A′ =－0.06234，B′ =－0.11468.有限元计算得出的A，B 的值与据式(2)计算的理论值如表1 所示.应变释放系数有限元计算值与式(2)理论计算值分别相差－2.3%和13.6%，说明根据具体钻孔试验情况对应变释放系数做修正是必要的.

表1 应变释放系数有限元计算值与理论计算值的比较

1.4 机械钻孔附加应变的标定

由于钻孔采用的是一种机械方法，不可避免的会产生附加应变［7］，式(1)中的计算公式εr并未考虑此因素(主要由钻孔产生的热效应和径向的挤压等构成)的影响.由于钻孔匀速且为定轴转动故假设这些影响因素引起附加应变的环向梯度为零.设径向附加应变为¯ε，则径向总释放应变εr′为:

在应用钻孔法检测金属残余应力时，钻孔附加应变一般取经过充分退火的零应力块预先测出.考虑到附加应变会受待测构件材料、钻孔技术、钻头锋利程度以及采用应变花尺寸和钻孔半径等因素影响.本文提出下述方法对附件应变进行标定.

对于钢结构中某受单向拉伸(或压缩)梁(一般取两端铰接的钢梁)，把应变花中0?应变片延轴向(主应力方向)粘贴，如图6 所示，图中σ1，σ2为主应力方向.

图6 单向受拉(或压)梁应变花布置

由式(7)可知，三个应变片方向测得的总应变为:

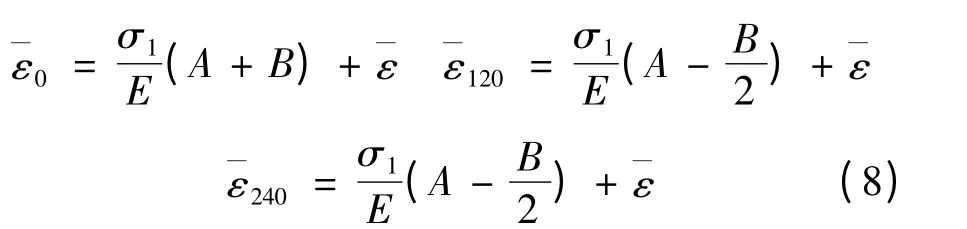
由式(8)可求解得:

图7 钻孔试验效果

由于测试中采用的是同一种钻孔工艺，故钻孔附加应变¯ε 可由上述单向受拉(压)梁标定.那么各构件主应力计算公式由式(3)和(4)变为:

式中，ε0′，ε120′，ε240′为各待测点应变计测得的应变值为附加应变的标定值.

2 钻孔法测试方法实验数据分析方法

2.1 钻孔数据采集方法

为了保证钻孔测试精度，采用专门定制的RSD－I 型残余应力打孔仪，钻孔过程中应变值采用定制的DH3818－7 静态数据采集仪记录，钻孔过程中数据采样间隔为10s，待钻孔结束，数据稳定后停止采数.钻孔仪器及效果如图7 所示.

2.2 附加应变 的标定

在测试之前，需通过对某单向受拉(压)梁进行多次钻孔测试的方式来标定附加应变.由实验可得出58.52με.据文中式(11)计算公式可计算求得=－28.07με.本次测试共做了5 次标定试验，其计算结果见表2，从表2 中可看出，第3 次测试数据偏差较大，故取其他四次测试结果均值作为最终标定结果:=－28.80με.由测试可知占测试应变，和的19%，48%和49%，可见，对应力计算公式做附加应变的修正是非常必要的.

表2 附加应变的标定值

3 测试结果

本文应用上述方法，对天津某大型钢结构建筑工作应力进行了检测.下表列出了其中一些结构构件的工作应力检测结果.

表3 某大型钢结构建筑部分构件工作应力测试结果

4 结 论

从本文测试过程及结果可以看出，钻孔法用于实际工程钢结构工作应力的测试，无论是理论还是在实际操作中都是可行的.但在测试时应该注意以下几点.

(1)钻孔位置精准度会对结果产生较大影响，需用显微镜检查各测点钻孔位置，以确该次测试数据可用.

(2)钻孔法测试钢结构工作应力理论中的释放系数A，B 需要根据具体测试时的几何、物理参数做相应调整，从而确保测试结果的精度.

(3)钻孔过程应匀速缓慢，否则容易导致孔周产生过大的塑性区，不满足本文测试方法提出的假设，从而导致结果出现较大误差.

(4)整个测试过程中需要使用同种工艺做钻孔测试以确保附加应变的¯ε 稳定性.

［1］ 王威，王社良，苏三庆，等.钢铁材料结构构件工作应力的检测方法及特点［J］.钢结构，2004，19(5):43－46.

［2］ Standard A.E837，Standard Test Method for Determining Residual Stresses by the Hole－Drilling Strain－Gage Method［J］.2008.

［3］ Aoh J N，Wei C S.On the Improvement of Calibration Coefficients for Hole－drilling Integral Method:Part I－Analysis of Calibration Coefficients Obtained by a 3－D FEM Model［J］.Journal of Engineering Materials and Technology，2002，124(2):250－258.

［4］ 陈惠南.盲孔法测量残余应力A，B 系数计算公式讨论［J］.机械强度，1989，11(2):31－36.

［5］ 裴怡，包亚峰.盲孔法测定时计算公式中A，B 值的研究［J］.机械强度，1997，19(1):18－21.

［6］ 郑建毅，何闻，沈润杰.小孔法中校准系数的有限元数值标定技术研究［J］.机械工程学报，2011，47(14):26－31.

［7］ 翟传明，邸小坛，白伟亮，等.盲孔法检测既有金属结构应力的研究［J］.建筑科学，2011，1.