爆炸荷载下钢筋混凝土梁的变形和破坏*
李猛深,李 杰,李 宏,施存程,张 宁
(1.沈阳军区司令部工程科研设计所,辽宁 沈阳 110162;2.解放军理工大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007;3.南京理工大学机械工程学院,江苏 南京 210009;4.第二炮兵指挥学院,湖北 武汉 430012)
爆炸荷载下钢筋混凝土梁的变形和破坏*
李猛深1,2,李 杰2,3,李 宏1,施存程4,张 宁2
(1.沈阳军区司令部工程科研设计所,辽宁 沈阳 110162;2.解放军理工大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007;3.南京理工大学机械工程学院,江苏 南京 210009;4.第二炮兵指挥学院,湖北 武汉 430012)
利用爆炸压力模拟器进行钢筋混凝土简支梁爆炸冲击实验,详细介绍了实验设计,通过实验系统分析了钢筋混凝土(RC)梁变形破坏特征以及钢筋作用机理和对变形破坏的影响,并建立了RC梁的分离式有限元模型,利用LS-DYNA分析了实验过程,对计算结果与实验结果进行了比较,分析了误差产生的原因,得到了爆炸冲击荷载作用下RC梁的损伤破坏特征和机理,可为毁伤评估和结构抗爆设计提供参考。
爆炸力学;破坏特征;有限元;钢筋混凝土梁;爆炸荷载
恐怖活动以及生活、生产事故,都可使建筑物遭受偶然性爆炸作用[1],造成重大经济损失和人员伤亡。例如:1995年,美国Oklahoma市联邦大楼恐怖袭击案, 爆炸造成大楼倒塌,168人死亡;2007年,我国山西大同市居民楼爆炸事故,造成4间房屋坍塌,9人伤亡。
钢筋混凝土(RC)结构主要由梁、板、柱等构件组成,研究RC梁在爆炸冲击条件下的破坏模式和抗爆性能,对于提高钢筋混凝土结构的抗爆安全性具有重要的理论意义和工程价值[2]。
钢筋混凝土属于典型非均匀介质,爆炸荷载下,高温高压气体与材料发生强烈的动态流固耦合,应力波在构件中的传播、折射和反射,使其处于复杂应力状态。由于理论分析的困难,常采用实验和数值方法进行研究。
陈肇元[3]使用“C-3”快速加载实验机,对钢筋混凝土梁、柱、迭合板构件进行爆炸曲线形式加载,获得快速变形下构件的开裂破损形态,考察了快速加载对构件的最大抗力、延性等方面的影响。张想柏等[4]进行了有限厚度钢筋混凝土板接触爆炸实验,依据现场实验归纳出爆炸成坑、爆炸震塌、爆炸贯穿和爆炸冲切形态。匡志平等[5]对3根两端铰接低配箍钢筋混凝土梁在爆炸荷载下的力学性能进行实验研究, 分析了梁的裂缝、应变和挠度变化情况等。
物理实验需要耗费大量人力财力,但能提供的信息有限。数值模拟则为钢筋混凝土构件受力性能研究提供了一种有力的分析工具。数值模拟中有限元法较为成熟,其基本思想是对结构先离散再综合,基于材料本构关系、平衡方程和变形协调这3个基本条件解决问题。例如:T.Krauthammer等[6-7]基于Timoshenko梁理论,考虑了钢筋和混凝土的材料非线性和应变率效应、反复加载效应以及合理的结构行为,提出了钢筋混凝土梁板结构在均布爆炸荷载下动态响应的简化数值分析方法。方秦等[8-10]在上述的梁理论基础上,采用非线性分层梁有限元法和有限差分法分析了钢筋混凝土梁和钢板与钢筋混凝土组合梁的动力响应和弯曲、弯剪及剪切破坏等破坏模式。M.Barbato[11]提出了一种简单高效的二维有限元模拟方法,能够准确预测FRP加固的钢筋混凝土梁的抗爆承载力。
本文中,采用实验分析和数值计算相结合的方法,分析爆炸冲击荷载作用下钢筋混凝土梁的损伤机理和破坏特征,以期为毁伤评估和结构抗爆设计提供参考。
1 钢筋混凝土梁的爆炸荷载实验
实验采用的爆炸压力模拟器(模爆器),内径1.9 m,如图1所示。实验数据由DH5939N高速数据采集记录仪记录。实验时导爆索(黑索金)点火起爆后,在模爆器腔内形成高压气体,高压气体通过栅格板,由于栅格板小孔的阻尼作用,改变了混乱的运动状态,形成均布的爆炸荷载。
采用C30混凝土自行配置浇注方形钢筋混凝土梁,尺寸为150 mm×150 mm×1 400 mm,保护层厚度为15 mm,通过支架固定于实验装置,相当于两边简支。为考察配筋率对试件破坏过程的影响,采用3种配筋方式BS、BM、BL,拉/压配筋分别为2∅10 mm、2∅12 mm、2∅16 mm,箍筋均为加密区∅8 mm@50 mm、非加密区∅8 mm@100 mm,配筋率分别为0.70%、1.01%、1.79%,具体如图2所示。为抑制钢筋混凝土梁的剪切破坏,对两端箍筋加密。

图2 钢筋混凝土梁尺寸与配筋Fig.2 Dimension and bar arrangement of RC beams
实验中需要测量爆炸波反射压力及试件截面应变,压力传感器置于试件两侧(见图1),钢筋应变片黏结于钢筋上(见图3(a)),混凝土应变片贴于试件顶部(见图3(b)、图3(c))。
实验前参照文献[12]对试件的动力荷载峰值承载力进行了估算,以选取合适的装药量(导爆索长度)。取相同的导爆索长度,以使作用在不同试件上的爆炸荷载大致相同,起爆后爆炸荷载瞬间升至峰值,随后呈三角形下降,持续时间在0.6 s左右,实验具体测得荷载曲线如图4所示。
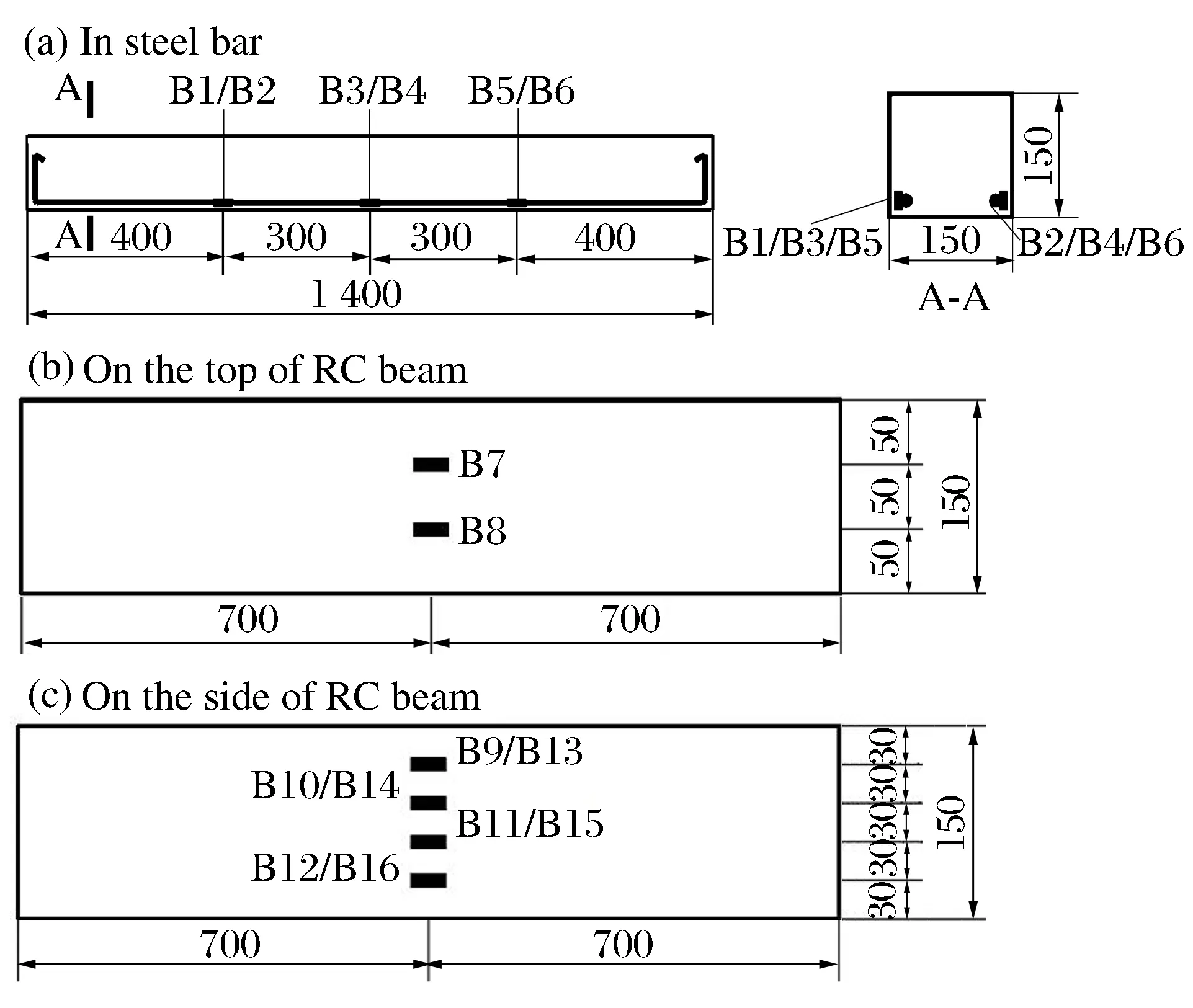
图3 应变片布置Fig.3 Strain gauges arrangement

图4 实测爆炸荷载曲线Fig.4 Experimental blast loading curves
由于爆炸波荷载破坏性较大,实验过程中一些应变片损坏,剔除明显已损坏的应变片可以得到试件关键截面应变曲线。实验后钢筋混凝土梁破坏情况如图5所示,具体描述见表1。表中,pr为预估动载峰值,pe为实际动载峰值。

表1 破坏现象综合描述Table 1 Description of failure phenomenon

图5 RC梁的破坏情况Fig.5 Damaged RC beams

图6 低配箍RC梁的破坏形态[5]Fig.6 Failure modes of RC beams with low strrups arrangement
由实验可以发现:(1)文献[5]中曾对低配箍钢筋混凝土梁在爆炸荷载作用下的力学性能进行实验研究,发现在跨中部分没有出现明显裂缝的情况下,由于剪力所带来的斜压作用已使梁破坏,产生45°斜裂纹(见图6)。本文实验由于支座处箍筋加密,未出现此类破坏,配箍率对抑制剪切破坏作用明显。(2)随着拉应力的增大,RC梁跨中部分出现拉伸裂纹,由梁底板向上扩展,文献[13]中把裂纹分成一次和高次裂纹。一次裂纹由破坏表面起始并向内部扩展,达到钢筋配置处,由于原生的黏结联系(原生黏结关系,是指因混凝土收缩、黏结和微应力而产生的接触应力,摩擦力和钢筋机械性能(其上的网纹)的联系被称作次生黏结关系),钢筋阻碍了周围的混凝土层自由变形,只有在原生黏结关系弱化的前提下,一次裂纹端部才可能进入到钢筋的表面附近。发生这种弱化时,钢筋出现相对于裂纹的移动,裂纹的出现使钢筋的拉伸量与紧靠钢筋的水泥层的拉伸量不等。高次裂纹随着拉力的增大在低次裂纹之间产生,在高次裂纹形成期间,混凝土与钢筋之间的黏结关系具有次生黏结的特征(摩擦力和钢筋网纹机械咬合力)。(3)只要出现一次裂纹,就引起了受拉构件中内力的再分配。一次裂纹通过的横截面上的荷载,完全转移到钢筋上,而随着远离裂纹,由于次生黏结关系,拉力开始转移到混凝土上。(4)混凝土的破坏过程不是连续的,而是具有某种渐进性的动态特征。但局部黏结的断裂,发生的速度很快。钢筋由于原生黏结关系,起着阻碍这些变形速度的作用。(5)不同编号RC梁所受实际冲击波荷载接近,随着试件配筋率提高,试件裂缝数量增多,裂缝宽度减小,配筋率的增大对提高梁试件抗爆性能作用明显。
2 计算模型和材料参数
2.1 钢筋材料模型
不考虑温度的影响,钢筋本构模型采用LS-DYNA中的J-C模型,其应力-应变(应变率)关系如下:
(1)

利用VHS160/100-20实验机测试拉伸应变率2~80 s-1范围内钢筋动力性能,利用Matlab数学软件nlinfit非线性回归函数得到钢筋的模型参数(具体步骤不详细叙述),如表2所示。根据实验,取钢筋的极限拉应变为0.16。

表2 钢筋计算参数Table 2 Calculation parameters of reinforcing bar
2.2 混凝土材料模型
混凝土采用Karagozian & Case Concrete (KCC)模型[14],该模型综合考虑了大变形、高应变率和高静水压的影响,适于混凝土结构在爆炸冲击等强动载作用下的计算分析。自1994年推出后经过了多次改进,KCC模型并得到了广泛应用。
2.2.1 破坏准则
KCC模型通过定义屈服极限面、最大强度极限面和残余强度极限面,描述材料的破坏过程:
(2)
式中:a0i、a1i、a2i分别代表屈服极限面、最大强度极限面和残余强度极限面的相关参数,通过实验确定;p为静水压,θ为Lode角,r(θ)为Lode角对极限面的影响。随着静水压力的提高,残余强度面与最大强度面重合,代表了高静水压下混凝土由固体向拟流体状态的转化。最大强度面和屈服极限面、残余强度极限面之间的部分,代表了混凝土的应变强化和应变软化效应,位于这3个极限面之间的失效面通过内插法得到:
(3)
式中:η(λ)为插值函数,λ为损伤参量。KCC模型通过引入应变率强化系数反映混凝土的率敏感性,强化系数为C时3个极限面调整为:
fi(p,θ)=Cr(θ)Fi(p)
(4)
2.2.2 损伤描述
KCC模型通过等效塑性应变的累积表征材料的损伤:
(5)

Δλ=b3fdkd(εV-εV,yield)
(6)
(7)
式中:kd为比例因子,εV为拉静水压下的体应变,εV,yield为屈服点的体应变,b3为调节参数,fd为将应力状态限定在拉静水压附近的参数。
2.2.3 状态方程
材料的变形可分解为体变和畸变两部分,畸变部分可通过确定上述极限面利用塑性流动法则求解,体变部分通过状态方程描述。加载时(压缩),CKK模型的状态方程为:
p=Q(εV)+γT(εV)E
(8)
式中:Q为与体应变εV对应的静水压,γ为Grüneisen系数,T为与εV对应的温度,E为单位体积内能。卸载时,材料延着与峰值应变对应的体积模量卸荷,重新加载时,材料延着初始卸荷曲线路径直到卸荷初始点,然后沿着方程(8)的曲线继续加载。
由于混凝土的绝大多数参数均与材料强度相关,仅通过输入材料强度和单位转换量,CKK-REL3模型具有参数自动生成功能,利用该功能,根据实验取混凝土强度为36.9 MPa。

图7 RC梁侧面的最终破坏形态Fig.7 Failures modes of RC beam side
采用显式动力分析软件LS-DYNA对上述实验的试件进行数值分析,建立钢筋、混凝土的分离式有限元模型,其中钢筋采用梁单元,混凝土采用六面体单元,不考虑钢筋与混凝土间的黏结滑移,两者通过共用节点连接。
为节省计算时间,利用截面的称性,取梁试件1/2结构进行计算,并在对称面上施加对称边界条件。考虑到计算精度及计算时间等要求,混凝土单元网格取为10 mm×10 mm×10 mm,计算荷载采用实验测得的爆炸波反射压力时程。
3 结果分析
根据计算的混凝土损伤发展历程,可以大体反映混凝土中的裂缝发展过程。在均布爆炸荷载作用下,钢筋混凝土梁底部首先产生一次裂纹,由梁底部向上发展,随着变形的加剧,在一次裂纹间产生高次裂纹,最终导致在梁的跨中区域出现密集裂纹。图7为实验的最终形态与数值计算的最终损伤区域的比较,由图可知,计算结果与实验现象基本吻合。

图8 实验与数值模拟的应变曲线Fig.8 Strain curves of experimental and numerical simulation
将实验所得和有限元计算所得的应变曲线进行对比,如图8所示。实验过程中,由于BM跨中顶部混凝土应变片及BS跨中钢筋应变片损坏,未进行对比。可知材料的应变曲线趋势基本吻合,峰值应变和残余应变存在一定的误差。由于实验中没有布置位移计,仅对试件的跨中残余变形进行比较(见表3)。表中,de为实测跨中位移,dn为计算跨中位移。数值计算结果与实验值误差在10%左右。

表3 跨中位移Table 3 Midspan displacements
数值模拟跨中位移偏小,主要原因为:(1)数值模拟为较理想的情形,真实构件为典型的非均匀介质,其变形破坏受到初始缺陷的影响;(2)钢筋与混凝土之间共用节点,不考虑两者间的滑移,与实际情况存在偏差;(3)数值计算没有考虑温度的影响,实际情况是爆炸产生的高温使钢筋混凝土的强度降低。
计算结果表明,KCC模型可以较准确地模拟爆炸冲击荷载作用下混凝土的性能,但不够完善,计算结果误差较大。更合理的本构模型开发是下一个阶段进行的工作,当前需要解决的问题是,如何在物理参数变化的宽阔范围内完全符合实际地描述介质的行为,这些参数是应变、应力、应变速率、温度等。
4 结 论
(1)爆炸冲击作用下混凝土裂纹可分为一次和高次裂纹。一次裂纹由破坏表面起始并向内部扩展,由于裂纹区原生黏结关系的弱化,使裂纹进入到钢筋的表面附近,一次裂纹通过的横截面上的荷载,完全转移到钢筋上。而随着远离裂纹,由于次生黏结关系,拉力开始转移到混凝土上,高次裂纹随着拉力的增大在低次裂纹之间产生,高次裂纹形成期间,混凝土与钢筋之间的粘结关系具有次生黏结的特征。
(2)混凝土的破坏过程不是连续的,而是具有某种渐进性的动态特征。但局部黏结的断裂,发生的速度很快。钢筋由于原生黏结关系,起着阻碍这些变形速度的作用,配筋率的增大对提高梁试件抗爆性能作用明显,随着试件配筋率提高,试件裂缝数量增多,裂缝宽度减小。
(3)混凝土KCC模型可以大致准确地模拟爆炸冲击荷载作用下混凝土的性能,但数值分析与实验结果也存在一定误差。主要原因在于:(a)缺乏理想的模拟结构中钢筋层与混凝土之间相互作用过程的方法;(b)钢筋混凝土为典型的非均匀介质,应力波在构件中的传播、折射和反射,使其处于复杂的应力状态,难以通过数学手段进行合理描述;(c)爆炸荷载作用下,高温高压气体与材料发生强烈的动态流固耦合,其热动力学效应不能忽略。
(4)更精确地描述爆炸冲击荷载作用下钢筋混凝土的动力响应过程,需要在本构模型方面继续做大量的工作。一个合理的本构模型,应在物理参数变化的宽阔范围内完全符合实际地描述介质的行为,这些参数是应变、应力、应变速率、温度等。
[1] 高康华,金丰年,王德荣,等.建筑物内爆炸荷载研究综述[J].中国工程科学,2013,15(5):59-64. Gao Kang-hua, Jin Feng-nian, Wang De-rong, et al. Review on internal explosion loading of building[J]. Engineering Science, 2013,15(5):59-64.
[2] 师燕超,李忠献.爆炸荷载作用下钢筋混凝土结构破坏倒塌分析研究进展[J].土木工程学报,2010,43(增刊):83-91. Shi Yan-chao, Li Zhong-xian. State-of-the-art in damage and collapse analysis of RC structures under blast loading[J]. China Civil Engineering Journal, 2013,43(suppl):83-91.
[3] 陈肇元.钢筋混凝土结构构件在冲击荷载下的性能[M].北京:清华大学出版社,1986.
[4] 张想柏,杨秀敏,陈肇元,等.接触爆炸钢筋混凝土板的震塌效应[J].清华大学学报(自然科学版),2006,46(6):765-768. Zhang Xiang-bai, Yang Xiu-min, Chen Zhao-yuan, et al. Explosion spalling of reinforced concrete slabs with contact detonations[J]. Journal of Tsinghua University (Science and Technology), 2006,46(6):765-768.
[5] 匡志平,杨秋华,崔满.爆炸荷载下钢筋混凝土梁的实验研究和破坏形态[J].同济大学学报:自然科学版,2009,37(9):1153-1156. Kuang Zhi-ping, Yang Qiu-hua, Cui Man. Experiment research and failure modes analyses of RC-beams under blast loading[J]. Journal of Tongji University: Natural Science Edition, 2009,37(9):1153-1156.
[6] Krauthammer T, Shahriar S, Shanaa H M. Response of reinforced concrete elements to severe impulsive loads[J]. Journal of Structural Engineering, 1990,116(4):1061-1079.
[7] Krauthammer T, Assadi-Lamouki A, Shanaa H M. Analysis of impulsively loaded reinforced concrete structural elements(Ⅱ): Implementation[J]. Computers and Structures, 1993,48(5):851-860.
[8] 方秦,柳锦春,张亚栋,等.爆炸荷载作用下钢筋混凝土梁破坏形态有限元分析[J].工程力学,2001,18(2):1-8. Fang Qin, Liu Jin-chun, Zhang Ya-dong, et al. Finite element analysis of failure modes of blast-loading RC beams[J]. Engineering Mechanics, 2001,18(2):1-8.
[9] 柳锦春,方秦,龚自明,等.爆炸荷载作用下钢筋混凝土梁的动力响应及破坏形态分析[J].爆炸与冲击,2003,23(1):25-30. Liu Jin-chun, Fang Qin, Gong Zi-ming, et al. Analysis of dynamic responses and failure modes of RC beams under blast loading[J]. Explosion and Shock Waves, 2003,23(1):25-30.
[10] 方秦,吴平安.爆炸荷载作用下影响RC梁破坏形态的主要因素分析[J].计算力学学报,2003,20(1):39-42. Fang Qin, Wu Ping-an. Main factors affecting failure modes of blast loaded RC beams[J]. Chinese Journal of Computational Mechanics, 2003,20(1):39-42.
[11] Barbato M. Efficient finite element modeling of reinforced concrete beams retro fitted with fibre reinforced polymers[J]. Computers and Structures, 2009,87(3/4):167-176.
[12] GB 50038-2005 人民防空地下室设计规范[S].北京:中国建筑工业出版社,2005.
[13] Мяновский К М. Механизм трещинообразования железобетонных элементов с дисперсным армирова-нием при растяжении[M]. ВЦП НТЛиД, 1979.
[14] Malvar L J, Crawford J E, Wesevich J W,et al. A plasticity concrete material model for DYNA3D[J]. International Journal of Impact Engineering, 1997,19(9):847-873.
(责任编辑 丁 峰)
Deformation and failure of reinforced concrete beams under blast loading
Li Meng-shen1,2, Li Jie2,3, Li Hong1, Shi Cun-cheng4, Zhang Ning2
(1.EngineeringResearchandDesigningInstitute,ShenyangMilitaryAreaCommand,Shenyang110162,Liaoning,China;2.StateKeyLaboratoryofDisasterPrevention&MitigationofExplosion&Impact,PLAUniversityofScienceandTechnology,Nanjing210007,Jiangsu,China;3.SchoolofMechanicalEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China;4.TheSecondArtilleryCommandCollege,Wuhan430012,Hubei,China)
With explosion pressure simulator, blast experiments were carried out to investigate the deformation and damage of concrete (RC) beams. The experimental design and parameters are described in detail. The experimental result shows the failure characteristics of RC beams and the role that rebars act. With LS-DYNA, three-dimensional separated finite element models of RC beams were established to simulate the experiment. The simulation and experimental results are contrasted to investigate the damage mechanism and failure characteristics. The article also figures out the reason of simulation errors. The research provides reference for damage assessment and anti-blast design.
mechanics of explosion; failure characteristics; finite element; reinforced concrete beam; blast loading
10.11883/1001-1455(2015)02-0177-07
2013-07-10;
2014-01-15
国家自然科学基金青年科学基金项目(51308543);中国博士后科学基金项目(2014M552688)
李猛深(1984— ),男,博士,工程师; 通讯作者: 李 杰,lijierf@163.com。
O383.2 国标学科代码: 1303520
A

