基于高速实车驾驶数据的驾驶人跟车模型研究*

袁 伟，付 锐,2，马 勇，郭应时，杜春臣

(1.长安大学汽车学院，西安 710064； 2.长安大学，汽车运输安全保障技术交通行业重点实验室，西安 710064)



2015120

基于高速实车驾驶数据的驾驶人跟车模型研究*

袁 伟1，付 锐1,2，马 勇1，郭应时1，杜春臣1

(1.长安大学汽车学院，西安 710064； 2.长安大学，汽车运输安全保障技术交通行业重点实验室，西安 710064)

通过实车试验采集驾驶人在高速公路的跟车数据，分析了跟车过程中加速、稳速和减速阶段的划分标准，探讨了稳速跟车阶段驾驶人的期望跟车间距与跟车速度之间的关系，建立期望间距跟车模型，并与自适应巡航控制(ACC)系统所用的安全距离模型进行对比。结果表明：加速和减速阶段，驾驶人的反应并非对称，加速阶段的车辆状态变化更频繁；在稳速跟车阶段，驾驶人的期望跟车间距随车速的升高而增加；与安全距离模型相比，所建立的期望间距跟车模型更符合驾驶人跟车习惯。

交通安全；跟车；稳速阶段；期望跟车间距；反应时间；驾驶人

前言

跟车行为是汽车驾驶过程中最常见且最重要的行为之一，驾驶人的跟车行为与交通安全密切相关。研究人员对跟车过程的研究已达半个多世纪，建立了很多侧重于交通流理论、控制算法或驾驶人心理、生理等方面的跟车模型。文献[1]中对GM模型、安全间距模型(又称避撞模型，简称CA模型)、线性模型、反应点模型和模糊逻辑模型等典型跟车模型进行了详细对比和评述。文献[2]中详细介绍了各种基本跟车模型(包括最优速度模型、全速差模型、Newell跟车模型)和基于驾驶策略的跟车模型(如Gipps模型与智能驾驶人模型IDM)，并探讨了IDM与自适应巡航控制(ACC)系统的关系及其在ACC系统中的应用。总的来讲，跟车模型是对驾驶人跟车行为的一种理论描述，能够反映前车状态变化引起自车参数变化的过程。从这种反应机理上讲，现有的跟车模型主要包括基于保持安全制动间距的跟车模型和基于刺激-反应机理的跟车模型。其中基于保持安全制动间距的CA模型通过牛顿运动定律，结合车辆制动性能和驾驶人反应时间等计算出特定理论安全跟车距离[3]；基于刺激-反应机理的GM模型[4]以前后车之间的相对速度作为刺激标准，以自车加减速度表示反应情况，并引入灵敏度作为调整系数，研究跟车过程中各参数之间的相互关系。

跟车行为非常复杂，很难将其视为单一状态进行分析。为了更好地解释跟车行为，文献[5]～文献[7]中将其划分为加速阶段、稳速跟车阶段和减速阶段。然而大部分跟车模型只侧重于稳速跟车阶段的研究，而对加速和减速阶段跟车特性的分析不足，且对跟车阶段的划分也不够清晰。由于国内研究多借鉴国外标准，因而缺少对于中国驾驶人适用性的验证。此外，驾驶人在稳速跟车时，跟车间距并非恒定不变，而是在期望距离附近波动。文献[8]中在跟车行为研究的基础上，提出了基于期望间距的跟车模型。期望间距能形象地反映后车跟车行为，但现有的期望间距模型，其跟车数据多在车速较低的范围内获取，或是在特定路段下专门采集，缺乏在真实路况下的数据作为建模依据，因此在ACC系统应用方面存在很多问题。

本文以驾驶人在高速公路的驾驶数据为基础，从中筛选出跟车数据，分析加速、稳速和减速等阶段的跟车行为特性和稳速跟车状态下期望跟车间距随车速、车距之间的关系，并在此基础上建立逼真的期望间距跟车模型，为ACC系统的应用提供理论依据。

1 试验设计

1.1 试验道路

选取两段高速公路作为试验路段，其中路段1为G25高速公路青山入口到长兴出口，全长40.5km，双向4车道，中等交通量，限速110km/h。路段2为G40高速公路香王入口到蓝田东出口，全长57.4km，同样为双向4车道，中等交通量，限速100km/h。

1.2 被试驾驶人

共选取39名男性驾驶人进行试验，年龄为25～50岁，平均年龄为40.9岁，标准差为6.01岁；驾龄为4～30年，平均驾龄为16.7年，标准差为7.2年。被试驾驶人基本信息见表1。

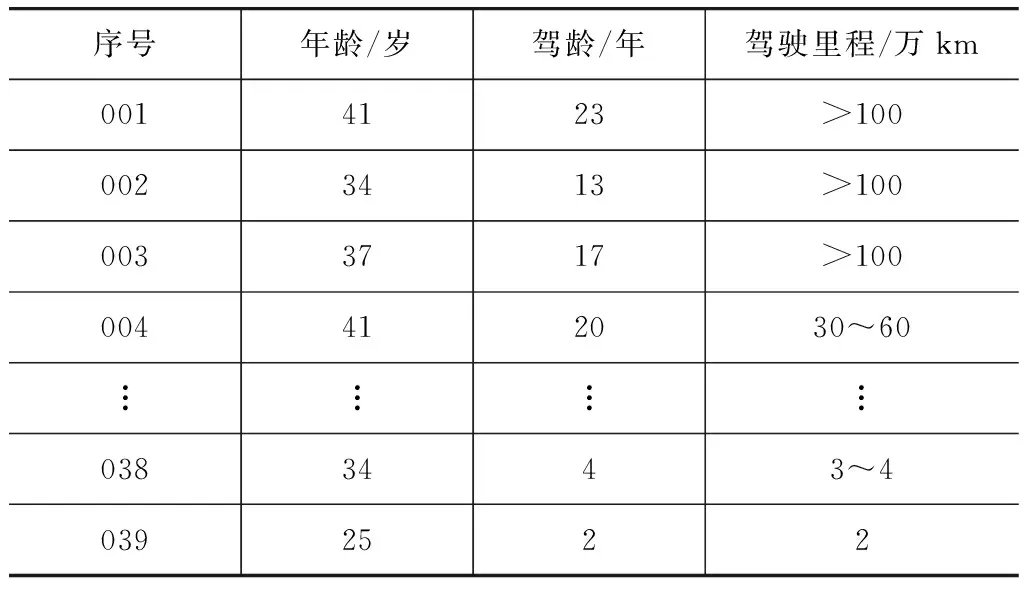
表1 被试驾驶人信息表

1.3 试验设备

试验车辆为大众途安牌自动挡多功能轿车，并安装数据采集仪器：两套分别安装在试验车前端和后部的毫米波雷达系统，测量本车与目标车之间的距离和相对速度等数据；视频监控系统采用多路工业摄像机对驾驶人的操作行为和车辆周围交通环境进行监控，并为后续的数据分析提供完整的试验过程回放；加速踏板行程传感器实时采集加速踏板行程数据。

1.4 试验过程

在试验过程中，为保证驾驶行为的真实与可靠性，被试驾驶人不佩戴任何仪器设备。试验开始前告知被试驾驶人试验线路，让其按照日常驾驶习惯自由驾驶。数据全程自动采集，即记录从驾驶人起动车辆到最终完成试验整个过程的数据。

2 跟车数据筛选

从驾驶人角度考虑可将跟车行为分为两种：稳速跟车和非稳速跟车。稳速跟车行为指驾驶人跟随前车行驶，没有换道意图，这种稳速跟车行为通常持续10s以上。非稳速跟车行为指驾驶人在有意换道或超车过程中与前车之间保持较小距离的跟车行为，这种情况通常持续时间很短，且两车之间的距离较近，一般为驾驶人为完成其他操作的过渡阶段。本文主要研究稳速跟车行为。

首先通过观看驾驶人行车视频，挑选出跟车持续时间大于10s的稳速跟车行为时段；然后剔除车辆行驶缓慢、堵车或者前车换道、本车换道、有车辆突然驶入本车与前车之间，或者前车超出雷达监测范围等情况时的数据。依据上述原则，从所有数据中初步挑选出样本323组，约14 139s，跟车距离在10～200m之间，并以10m为间隔，对各个区间的样本数和前后车速之间的相关系数进行统计分析(图1)。

稳速跟车时，前后车速之间应该有较强的相关性。由图1可见，在跟车间距140m处，前后车速相关系数出现极小值点，此后的样本较少；同时若按试验路段限速100km/h计算时，车距大于140m之后，车头时距将超过5.04s。因此认为当车距大于140m则不属于稳速跟车行为。此外，小于20m时跟车距离太近，而且样本较少，也不视为稳速跟车行为。为保证跟车数据的有效性，最终选取车距在20～140m的数据作为有效跟车数据进行分析。

3 驾驶人跟车特性

已有跟车行为的研究往往侧重于稳速跟车阶段，而忽略了加速和减速阶段。要准确分析跟车过程中前后车各参数之间的关系，即自车对前车刺激做出的响应，则有必要详细分析各阶段的跟车特性。

3.1 跟车阶段划分

跟车开始阶段，驾驶人不断加速接近前车，当与前车距离即将达到期望间距时，驾驶人不断调整状态，直至达到稳定。本文以此作为划分状态的方法。已有研究表明，稳速跟车阶段的相对速度(即前车速度vL减自车速度vF)维持在-2～2m/s之间。选取100组完整的跟车样本，分别统计相对速度在-2～-1m/s和1～2m/s之间的频率，其分布如图2和图3所示。

由图2和图3可见，在相对速度±1.5m/s附近自车速度波动最大，因此，本文选取-1.5～1.5m/s作为稳速跟车阶段的相对速度区间。

综合以上对稳速跟车行为3个阶段的理论分析与数据统计，以相对速度±1.5m/s作为加速、稳速和减速3个阶段的分界点，稳速跟车阶段(相对速度-1.5～1.5m/s)占据整个跟车过程的大部分时间，在该阶段驾驶人将跟车间距维持在期望跟车间距范围内。

3.2 跟车行为分析

3.2.1 稳速跟车阶段

由跟车理论可知，在稳速跟车阶段，前后车之间的相对位置关系并非一成不变，而是处于一种振荡过程，即自车驾驶人在小范围内调整车辆，使其维持在期望间距附近[9]。图4为两段跟车过程中跟车间距随相对速度的变化关系。

从图4可以清晰地看出，在跟车过程中，稳速跟车阶段(相对速度在-1.5～1.5m/s的阶段)占据大部分时间。此外，稳速跟车过程中相对速度和跟车间距并不恒定，而是在一定范围内波动，如图4所示呈螺旋状。其中，示例2是比较完整的一段跟车过程：驾驶人在有跟车意图时，不断接近前车，达到其期望间距时维持与前车车速平衡；当前车加速，且驾驶人不再有跟车意图时，两车间距迅速增加，跟车过程结束。

通过对稳速跟车阶段数据进行统计，得到不同车速下驾驶人的期望跟车间距，见表2。

表2 不同车速下的期望间距值

对上述跟车间距进行曲线拟合发现，用三次多项式对期望跟车间距均值与车速进行拟合时，其拟合优度最佳。将期望间距的最大值、最小值也进行曲线拟合。选取最佳的三次多项式拟合函数，如图5所示。

此外，在稳速跟车阶段，加速踏板行程均值维持在30%左右，随着车速的增加呈微小增加趋势。驾驶人根据个人经验不断对跟车间距进行判断，因此，加速踏板行程也处于不断调整状态，与车速相关性较小，分布相对均匀。

3.2.2 加减速阶段

在加速(减速)阶段，自车快速靠近(远离)前车，两车间距逐渐缩小(变大)，相对速度逐渐减小(变大)。图6为两段跟车过程中跟车间距与相对速度的变化关系。

从图6可以大致看出，加速阶段和减速阶段并不对称，加速阶段持续时间更长，间接验证了文献[10]和文献[11]中的结论。另外，在跟车间距即将达到驾驶人的期望间距时，驾驶人将进行多次加速/减速以调整与前车的相对速度，从而使自车与前车达到一种大致的稳速间距，即进入稳定跟车阶段。

3.3 加速度特性分析

通过上述跟车过程的研究，分析自车加速度的变化规律。

3.3.1 反应时间

滞后性是跟车行为的特点之一，即自车驾驶人感知前车状态的变化需要一定的反应时间。要讨论加速度的变化规律，首先要分析反应时间。参照文献[6]的方法，本文采用分析自车(后车)与前车速度峰值在时间序列上的差值，来计算驾驶人的反应时间。

从试验数据中选取样本83个，其中加速状态43个，减速状态40个。分别对加速状态和减速状态的反应时间做频率统计分析，在剔除异常样本(加速状态3个，减速状态2个)后，其频率统计如图7和图8所示。

从统计结果可知：加速状态下驾驶人反应时间均值为2.06s，低于均值的驾驶人约占70%；减速状态下反应时间均值为1.81s，低于均值的驾驶人约占66%；减速状态的反应时间小于加速状态。

分析原因，笔者认为：在高速驾驶时，当发现前车加速后，出于限速和安全驾驶考虑，自车驾驶人一般并不会立即随之加速，而是先确定自车当前车速，然后再根据具体情况做出是否加速(和多大加速度)跟车的判断，因而表现为速度峰值滞后时间较长；而当发现前车减速时，出于安全考虑，自车驾驶人一般会立即随之减速(无须判断自车速度)，因而表现为速度峰值滞后时间较短。但是，本文中得出的驾驶人反应时间整体仍高于已有结论(一般为1s左右)，这一方面是由于驾驶人期望跟车间距在一定范围内波动，如果未超出其期望间距阈值，则驾驶人一般不会进行加速或减速操作(表现为前车速度变化而自车速度未变)，从而使反应时间计算值偏长；另一方面也可能与驾驶人在高速公路操作更谨慎有关[12-13]。

3.3.2 加速度

由前文可知，稳速跟车过程也包含了加速行驶和减速行驶，并且这两种状态下驾驶人的反应时间也不同，但二者相差不大，为方便计算将反应时间统一设为T。

首先，从稳速跟车数据中挑选加速状态和减速状态样本，对样本中自车车速按照每0.1s的间隔计算加速度；然后，根据驾驶人反应时间(取T=1.8s)，分别筛选出反应操作之前对应的车速、与前车的相对速度、跟车间距。分析发现，前车加减速时，自车加速度与自车驾驶人反应操作前一时刻的两车相对速度显著相关(图9)。而与跟车间距无显著相关性。因此，本文不对跟车间距这种刺激特性作分析。

4 模型建立与验证

通过对跟车行为的分析，揭示了驾驶人在跟车过程中的行为特性，本文中以此为依据，建立如下符合实际的跟车模型。

期望跟车间距均值：

D均值=0.0004vF3-0.1143vF2+10.19vF-263.3

(1)

最大跟车间距：

Dmax=0.001vF3-0.2584vF2+22.5vF-577.2

(2)

最小跟车间距：

Dmin=0.0003vF3-0.0582vF2+4.738vF-108.2

(3)

自车加速度随前车速度的变化规律：

a(t+T)=0.5084v′(t)+0.0643

(4)

式中：vF为自车速度；T为驾驶人反应时间，取1.8s；v′(t)为相对速度，v′(t)=vL-vF，vL为前车速度，m/s。

本文虽然以实际道路跟车数据为基础建立了跟车模型，但模型能否准确描述高速公路跟车行为，是否优于已有的跟车模型，则需要验证。笔者选用PreScan软件作为场景仿真平台，建立高速公路场景，车辆行驶控制用Matlab/Simulink模块实现。同时，以现阶段大部分ACC系统采用的马自达安全距离模型作为对比。马自达安全距离模型的表达式为

(5)

式中：aF为自车制动减速度，6m/s2；aL为前车制动减速度，8m/s2；t1为车辆减速时间，0.1s；t2为系统延迟时间，0.6s；d0为车辆停止后车头间距，5m。

具体仿真内容如下：在三车道高速公路上，试验车在中间车道以期望车速100km/h行驶，当试验车正前方有车辆时，如果距离小于期望(安全)距离范围，试验车减速；如果距离超出该范围，以期望车速100km/h行驶；如果在该范围内，保持稳速跟随前车行驶。当前方没有车辆时，以期望车速100km/h行驶。此外，该场景也包含了试验车前方有车辆驶入和驶出等情况，与实际高速公路情况比较接近，从而可以客观地比较期望间距和安全距离两种跟车模型。仿真场景如图10所示。

按照上述建立的场景与控制，以0.05s为步长进行仿真，安全距离跟车模型与期望间距跟车模型的仿真结果分别如图11和图12所示。

由图11和图12可见，与安全距离模型相比本文中提出的期望间距模型的跟车间距较小，而变动幅度较大。应用于ACC系统的安全距离模型，在应用方面不太符合驾驶人操作习惯，且跟车过程中制动报警过早。而本文提出的期望间距模型在保证具有较好“人性化”的同时，确保了跟车行驶安全性。

图12中，期望间距模型仿真得到的跟车距离曲线最低点小于最小期望间距，主要是没有优化控制策略，对于跟车间距的变化反应不够灵敏。此外，对比图11和图12可见，期望间距模型仿真曲线没有安全距离模型仿真曲线变化平滑、稳定，这主要是由于仿真控制策略的选择不当对于自车加速踏板行程的完整模拟比较困难，在以后研究中有待提高。

两种跟车模型自车加速度对比结果见图13。

通过图13的加速度对比得知，期望间距模型得到的自车较大的减速和加速时刻明显滞后于安全距离模型，这主要是因为期望间距模型保持的跟车距离小，并且期望间距模型先以较小的减速度减速，在车间距接近临界值时，才开始以较大减速度减速。从整个仿真过程看出，期望间距模型的加减速次数明显少于安全距离模型。此外，从仿真动画中可以清晰地看出，采用安全距离模型，在与前车距离还较远时，自车就开始制动，而期望间距模型只是松开加速踏板进行减速，并没有立即制动，这更符合驾驶人的习惯。

5 结论

本文中重点研究了高速公路实车试验过程中驾驶人的跟车特性，结合国外对跟车过程的划分标准，统计分析跟车过程各阶段的参数特性，并在此基础上建立了基于期望间距的跟车模型，通过和ACC系统应用的安全距离模型作对比，体现出期望间距模型存在一定的优越性。主要研究结论如下：

(1) 稳速跟车阶段是一种动态的平衡过程，跟车间距呈现螺旋状变化，在动态中保持驾驶人的期望跟车间距，且在高速跟车行驶时，期望间距的值小于安全跟车距离；

(2) 加减速阶段并非对称，加速阶段持续时间更长，在加速阶段和稳速阶段相邻处，车辆状态变化更频繁，目的是达到期望的跟车间距，在减速阶段，两车间距逐渐变大；

(3) 跟车行为作为一种刺激-反应模型，驾驶人对前车的响应有一定的反应时间，减速过程要比加速过程反应快，自车对前车的响应(加速度)呈现明显的线性变化规律；

(4) 对跟车过程的研究结论进行综合考虑，建立高速公路期望间距跟车模型并对模型进行仿真，结果表明：与ACC系统使用的安全距离模型相比，期望间距模型与驾驶人的驾驶习惯更为接近，能够为ACC系统智能化的应用提供理论基础。

应当指出的是，由于试验中稳定跟车阶段的跟车间距变化不大，在较短的距离变化范围内，加速度不能呈现明显的变化，因此自车加速度与跟车距离是否确无相关性，有待通过更多试验数据进行进一步验证分析。

[1] Brackstone M, McDonald M. Car-following: a Historical Review[J]. Transportation Research Part F: Traffic Psychology and Behaviour,1999,2(4):181-196.

[2] Treiber M, Kesting A. Traffic Flow Dynamics: Data, Models and Simulation[M]. Translated by Treiber M, Thiemann C. Berlin: Springer-Verlag,2013:157-204.

[3] Kometani E, Sasaki T. Dynamic Behaviour of Traffic with a Non-linear Spacing-speed Relationship[C]. Proceedings of the Symposium on Theory of Traffic Flow, Research Laboratories, General Motors,1959:105-119.

[4] Chandler R E, Herman R, Montroll E W. Traffic Dynamics: Studies in Car Following [J]. Operations Research,1958,6(2):165-184.

[5] Marsden G, Brackstone M, McDonald M, et al. A Comparison of Differing Driving Populations Using the ICC FOT Classification Scheme[C]. TRB 2003 Annual Meeting, Washington DC,2002:1-21.

[6] 张智勇.城市快速道路车辆跟驰模型研究[D].北京:北京工业大学,2002.

[7] Piccoli B, Rascle M. Modelling and Optimisation of Flows on Networks[M]. Berlin: Springer,2013.

[8] Hidas P. A Car-following Model for Urban Traffic Simulation[J]. Traffic Engineering and Control,1998,39(5):200-305.

[9] Wiedemann R, Reiter U. Microscopic Traffic Simulation: the Simulation System Mission, Background and Actual State[R]. Brussels: CEC,1992.

[10] Leutzbach W. Introduction to the Theory of Traffic Flow[M]. Berlin: Springer,1988.

[11] 王文清,王武宏,钟永刚.基于模糊推理的跟驰安全距离控制算法及实现[J].交通运输工程学报,2003,3(1):72-75.

[12] Makishita H, Matsunaga K. Differences of Drivers’ Reaction Times According to Age and Mental Workload[J]. Accident Analysis & Prevention,2008,40(2):567-575.

[13] 吴超仲,马晓凤,严新平.考虑驾驶员反应能力的跟驰模型[J].武汉理工大学学报(交通科学与工程版),2007,31(4):630-632.

A Study on Driver’s Vehicle-following Model Based on High Speed Real Driving Data

Yuan Wei1, Fu Rui1,2, Ma Yong1, Guo Yingshi1& Du Chunchen1

1.SchoolofAutomobile,Chang’anUniversity,Xi’an710064;2.KeyLaboratoryofAutomotiveTransportationSafetyTechnology,MinistryofTransport,Chang’anUniversity,Xi’an710064

The vehicle-following data of drivers are collected on expressway by real vehicle test, and the criteria for classifying the acceleration, deceleration an stable speed phases are analyzed. The relationship between driver’s desired inter-vehicle distance and vehicle-following speed in stable-speed phase is explored, and a vehicle-following model based on desired inter-vehicle distance is established and compared with safe distance model used in adaptive cruise control system. The results indicates that in acceleration and deceleration phases, driver’s response is not symmetrical, and the vehicle state changes more frequently in acceleration phase; while in stable-speed phase, the driver’s desired inter-vehicle distance increases with vehicle speed. It is shown that the presented vehicle-following model based on desired inter-vehicle distance is more in accordance with drivers’ driving habits.

traffic safety; vehicle-following; stable-speed phase; desired inter-vehicle distance; reaction time; driver

*教育部创新团队支持计划(IRT1286)、国家自然科学基金(61374196和61473046)和中央高校基本科研业务费专项资金(CHD2012TD006)资助。

原稿收到日期为2013年10月14日，修改稿收到日期为2013年12月31日。