基于区间不确定性的前悬架多目标可靠性优化*
张宝珍,阿米尔,肖思俊
(湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082)
2015124
基于区间不确定性的前悬架多目标可靠性优化*
张宝珍,阿米尔,肖思俊
(湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082)
为减小悬架定位参数在车轮跳动过程中的变化量,以改善整车的操纵稳定性,减小轮胎的磨损,提出了一种考虑不确定性因素的前悬架不确定性多目标优化方法。首先,在Adams/Car中建立某车轿麦弗逊式前悬架模型,并运用Adams/Insight进行悬架设计硬点参数的灵敏度分析。然后,利用基于薄板样条插值的高维模型描述技术构建了设计变量和不确定变量与目标函数之间的近似模型。最后,针对该近似模型运用双层嵌套的改进非支配排序遗传算法和隔代遗传算法进行多目标不确定性优化与可靠性优化,得到Pareto最优解集。结果表明,优化后悬架主要定位参数在车轮跳动过程中的变化量有不同程度的减小,说明整车的操纵稳定性有所改善。
悬架;不确定性优化;高维模型描述;多目标优化;可靠性优化;遗传算法
前言
麦弗逊独立悬架具有结构简单、非簧载质量小、发动机与转向系容易布置、适合同多种形式的弹簧相匹配和能实现车身高度的自动调节等优点[1]。但其主销轴线的位置在减震器与车身铰链中心和横摆臂与转向节铰链中心的连接线上。当悬架变形时,主销的轴线会随之改变,而引起前轮定位参数与轮距的相应改变,而且变化量可能很大。目前研究对悬架的优化大多属于确定性优化,即在对悬架动特性进行优化时,车辆其他结构参数和动力学参数都固定不变。不确定性分析与优化是近年来国内外工程领域的研究热点。近几十年来,国内外许多学者都致力于发展非概率的不确定性建模手段,并在此基础上提出了相应的非概率不确定性优化方法和理论,从而使不确定性优化问题得以方便、经济地求解[2-5]。悬架刚度和轮胎径向刚度等参数随着汽车行驶环境和工况的改变而在一定范围内不确定性变动,会影响悬架系统的功能,从而会使车辆悬架系统优化过程中引入不可忽略的系统参数不确定性[6-7]。
工程优化问题中,对于基于真实模型的嵌套优化,每次计算目标函数值都要调用费时的计算模型,而利用近似模型可以有效地解决这一问题[8]。目前,已经取得广泛应用的一些近似方法如响应面法、Kriging插值等,在处理低维和线性问题时都得到了很好的效果。而对于复杂的模型,随着维数和非线性程度的增加,构造近似模型所需的样本点和计算花费呈指数增长,使解决此类问题的计算效率大大降低[9],且这些近似模型近似非线性问题时的精度不高。针对这一问题,文献[10]和文献[11]中证明了可积函数可以分解为不同维数函数的叠加理论,这一理论表明,对于任意一个可以积分的函数f(x),在其积分空间内存在唯一的可以扩展的高维模型,这一模型是精确的,有确定的阶数。
本文中利用高维近似模型来提高优化效率与精度,运用不确定性优化方法,选取悬架螺旋弹簧刚度和轮胎径向刚度为不确定性量,将NSGA-II和IP-GA结合起来优化与改进相关悬架设计参数,对某轿车悬架定位参数进行不确定性多目标优化,以提高整车的操纵稳定性。
1 区间数不确定性优化与可靠性
1.1 不确定性优化模型的描述
在实际工程问题中,由于材料、几何特性、边界条件、制造与装配误差和使用环境等因素造成的误差互相耦合,可能使系统响应产生较大的偏差。本文中将螺旋弹簧刚度和轮胎径向刚度看作不确定量,其变动范围通过区间表示,只须知道参数的上界、下界,这种描述称为区间数描述[8]。利用区间描述参数的不确定性,则一般形式的非线性区间数优化问题的数学表达式可示为
(1)
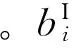
在本文中利用区间序关系将不确定性的优化转化成确定性的优化的主要内容是将不确定性的目标函数转化成确定性的目标函数。针对任何设计向量X,因不确定向量U的存在且f为U的连续函数,f(X,U)的取值范围是一个区间:
fI(X)=[fL(X),fR(X)]=[fc(X),fw(X)]
(2)
其中:
可以通过目标函数的中点和半径值来判断不同设计向量之间的优劣:设计向量X1优于X2,则X1处的目标函数区间优于X2处的目标函数区间,即
fc(X1)≤fc(X2),fw(X1)≤fw(X2)
则式(1)中的不确定目标函数可以转化为如下的确定性多目标优化函数问题:
(3)
1.2 可靠性模型
由于实际应用中不确定性的广泛存在,所以在问题求解时,为得到更好的求解精度,须考虑各种类型的不确定因素[12]。设不确定参数:
XI=[XL,XR]={X|XL≤X≤XR}
(4)
式中XL、XR分别为不确定变量的下界和上界。本文中的不确定量取螺旋弹簧的刚度和轮胎的径向刚度。对于一组不确定的变量x={x1,x2,…,xn},根据结构的失效准则,可以求得其结构失效函数:
M=g(x)=g(x1,x2,…,xn)=R-S
(5)
式中:R为引起失效的应力;S为抵抗失效的强度。
当g(x1,x2,…,xn)为x的连续函数时,M同样为一区间变量,设其均值和半径分别为Mc和Mr,则其可靠度指标为
η=Mc/Mr
(6)
按照可靠性理论,g(x)=0称为失效面,它将结构的空间分为失效域和安全域两部分,当g(x)>0时,认为结构处于安全状态。当η>1时认为结构是可靠的,该值越大表明结构的安全程度越高。
2 高维模型与遗传算法
2.1 高维模型(high dimensional model represen-
tations, HDMR)描述 高维模型为一种近似模型,可以将计算时间随非线性程度和维数增加按指数增长的隐函数转化为可以忽略高阶耦合项的多项式函数,并揭示了每个设计变量对近似函数的贡献量,得到一组显式函数表达式,大大减少了计算时间。同时反映了输入变量之间固有的线性或非线性关系及其相关性,有效地解决了非线性问题。设待求问题的设计变量可行域为An,则输出函数f(x)∈R与输入变量x∈An之间的映射关系可用HDMR[13-14]表示:

(7)
式中:f0为函数在中心点的函数值,后面依次为不同阶耦合项对函数的贡献量,耦合项可用薄板样条插值函数近似得到。
2.2 薄板样条函数
薄板样条函数是一种插值函数,是自然样条函数在多维空间的推广,可以表示多维空间曲面,在各学科均有广泛应用[15]。薄板样条插值函数的形式为

(8)
式中:‖…‖表示范数;φ为径向基函数,其形式为φ(r)=r2log(r),ri2=(x-xi)2+(y-yi)2;b0、b1、b2、ci为常数项系数,i=1,…,n。对于简单的1阶情况,函数的形式为
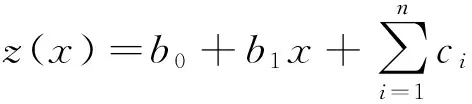
(9)
2.3 不确定优化算法
运用区间数将不确定性优化目标函数转化为确定性优化问题后是一个两层嵌套的优化问题,其外层的优化用来对设计向量进行寻优,而内层的优化用来计算不确定的目标函数和约束的区间。由于双层嵌套优化的存在,转化后的优化问题通常是非连续且不可导的[16],所以基于梯度的传统的优化方法很难对此有效求解。
由于NSGA-II具有求解Pareto解集准确和分散性好的优点[17],本文中外层采用在NSGA-II搜索架构的基础上加入精英保持策略,同时考虑遗传算法在子代个体中会出现重复个体,从而加大选优的工作量,在优化程序中又加入了去除重复个体算法的程序,这样,所采用的外层优化方法可更好地保持解的多样性,同时提高全局寻优能力和收敛速度。
内层优化算法采用隔代遗传算法(IP-GA),这是小种群遗传算法μGA的改进形式。μGA从传统的GA扩展而来,它不会过早收敛,搜索能力比传统的GA更强。为保证基因多样性,用重启策略取代变异操作,只要当前代符合收敛度要求,就随机产生相同规模的一个种群,而且新种群中会包含上一代中的最优个体。IP-GA在μGA的算法中增加了IP操作算子,通过对连续两个子代中的最优个体进行算术交叉运算以获取更优个体,进而大大提升收敛速度。
3 前悬架参数分析
3.1 前悬架虚拟样机模型的建立
根据某乘用车参数,在ADAMS/Car中建立该车带转向系统的麦弗逊前悬架虚拟样机仿真模型,如图1所示。
3.2 定位参数灵敏度分析
在建立优化近似模型前首先要对各个设计参数进行灵敏度分析,把灵敏度高的参数确定为设计变量,然后再建立优化近似模型。首先,在ADAMS/Car中进行前悬架两侧车轮同向跳动的试验,然后以此为基础在ADAMS/Insight模块中以2阶响应面的D优化设计方法进行试验设计,最后再返回到Car模块进行迭代仿真。图2~图5为灵敏度分析结果。
由灵敏度分析结果可知:减震器上安装点坐标、减振器下端点坐标、下控制臂外支点坐标、弹簧下安装点坐标和下摆臂后安装点坐标硬点值的改变对前轮定位参数值的影响相对较大,以这15个参数为设计因子在ADAMS/Insight中再次进行试验设计。
4 近似模型的建立与可靠性验证
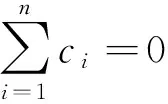
z(xi,yi)=vi
(10)
得到等式:
(11)
式中:Kij=φ(‖(xi,yi)-(xj,yj)‖);N的第i行为(1,xi,yi);b=(b0,b1,b2)T;O为3×3的零矩阵;0为3×1的零矩阵;c和v分别为由ci和vi构成的列向量;i,j=1,…,n。
由式(11)即可求出式(8)中各系数值,从而得到不同阶耦合项对近似模型的贡献量。通过本文算法构建的高维近似模型的相对误差见表1,从工程应用角度看,该模型的精度已经足够,可以用于后续的优化设计。

表1 近似模型的精度判断
5 前悬架不确定性优化
5.1 决策变量和不确定性变量的选取
通过3.2节中的灵敏度分析,选取车轮跳动过程中对定位参数影响较大的硬点值作为优化变量,并分别记作x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,同时悬架螺旋弹簧的刚度和轮胎的径向刚度参数会随着车辆行驶环境和工况的改变而在不确定性的范围内变动,本文的优化过程中考虑了这两个不确定性因素对悬架系统功能造成的影响。
考虑前悬架参数各个硬点位置空间布置的要求及整车行驶平顺性和操作稳定性对硬点位置的要求,得到优化变量的空间。
悬架螺旋弹簧的刚度和轮胎的径向刚度随使用环境和工况的改变而在不确定性的范围内变动。汽车的许多重要性能都与轮胎力学特性有关,轮胎的刚度特性对整车性能有极其重要的影响,在进行整车性能分析时,轮胎的刚度特性参数是必不可少的,研究表明,在汽车使用过程中轮胎变形程度、充气压力、激励频率、磨损和使用温度的变化等因素对轮胎径向刚度的影响较大[19];悬架螺旋弹簧在汽车行驶过程中,会承受高频的往复压缩运动,能起缓冲和减震的作用,其质量的好坏,对车辆的平稳性和安全性有非常重要的作用,它的性能取决于整机的要求,必须满足整机的质量特性。螺旋弹簧的热处理硬度在HRC43~48之间,由于硬度和刚度存在较强的线性关系,厂家通常给出其名义刚度值及其允许的变化范围[20]。本文在某轿车前悬架优化过程中,将轮胎径向刚度和螺旋弹簧刚度看作不确定量,其变动范围通过区间来表示,只须知道参数的上、下界,这种描述称为区间数描述。根据相关实验和资料,前螺旋弹簧刚度由于制造误差和行驶工况条件的瞬时变化,不确定性水平选为5%,轮胎的径向刚度由于使用过程中温度的改变和轮胎气压的不稳定等因素,选取不确定性水平为8%,分别记为x16,x17。
5.2 目标函数的建立
本文中优化的目的是减小车轮定位参数在车轮跳动过程中的变化量,从而增加整车的操纵稳定性和减小轮胎磨损。在前轮的4个优化定位参数中,主销内倾角和主销后倾角的主要作用是产生回正力矩即减小车轮转向过程中的操纵力。车轮的前束角是为适应车轮的外倾角而设定的参数,用来减小车轮的磨损。根据以上各个参数之间关系的分析,把前轮的定位参数分成2组,主销后倾角和主销内倾角为一组、车轮前束角和车轮外倾角为一组,通过加权的方法把每组整合成一个目标函数,则优化过程简化为
f1=w1y1+w2y2
(12)
f2=w3y3+w4y4
(13)
式中:wi为各个目标函数的权重系数。为方便本次优化计算,考虑各分目标函数对操纵稳定性和轮胎磨损速度的影响,本文中采用直接加权法选取权重系数。根据前面的仿真实验分析,确定各目标函数的取值范围,计算各目标函数的容限和权重系数。
经过加权组合后,车轮的4个定位参数优化问题转化为对车轮的转向节定位和主销定位两个目标的优化问题,系统的优化模型可表示为
(14)
5.3 计算流程
本文中将加入精英保持策略和去除重复个体的非支配排序遗传算法(NSGA-II)和隔代遗传算法(IP-GA)结合起来,在近似模型的基础上,以式(14)为优化目标,对前轮定位参数进行不确定性优化。首先,外层NSGA-II在悬架各硬点参数组成的设计空间内寻优,对于每个所取的设计向量进入内层IP-GA,在螺旋弹簧刚度和轮胎径向刚度组成的不确定参数空间内搜索,通过计算近似模型确定目标函数响应的上下界,进而得到目标函数响应的平均值。把内层优化结果反馈给外层优化算法,以帮助外层算法继续寻优,直到满足停止准则,则输出最后的Pareto最优解集,优化流程如图6所示。
由于得到的Pareto最优值的范围比较广泛,且不能进一步确定最优值大体的范围和结构的可靠度,为了更好地在Pareto前沿面中选择出最优解,引入可靠度作为最优解集的约束条件,进行进一步的比较计算,可靠度作为内层优化来实现约束,由式(6)得到安全系数,为保证悬架具有较高的安全性能,安全系数取值η=5,将符合可靠度的定位参数值输出,不符合的屏蔽掉,进行更进一步的目标寻优。为对比加入可靠度作为约束时对最优解的影响,将可靠度约束前后输出的Pareto最优解集进行对比,图7为加入可靠度前后的最优解集。
由图7可知,A点与D点分别为f1和f2的极小点,在AB段,f1的很小变化会引起f2的极大变化;在CD段,f2的很小变化就会引起f1的极大变化,这对决策者来讲,这两个区间都不是最好的选择区间,一般决策者都从变化比较平缓的BC段来选择最优点。对多目标优化的问题,往往不可能让每个目标同时取得最优值,只能在各目标之间进行协调权衡和折中处理,尽可能使每个目标接近最优。为了使f1和f2尽可能取最优值,本文中取比较平缓的BC线段的中点:
f*=(f1,f2)=(60.67,88.76)
对应响应值的设计变量:X=(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17)=(38.09,-652.13,529.05,8.92,-732.87,-63.44,-12.98,-801.32,-261.94,21.69,-715.14,264.41,431.39,-437.95,-187.5959,53.64,236.74)mm。
5.4 优化结果分析
把不确定性优化得到的最优硬点值重新带入ADAMS中仿真,得到各优化目标优化前后的对比,如图8~图12和表2所示。

表2 优化前后目标变量变化对照 (°)
由图8~图11和表2可知,不确定性优化后,除主销后倾角外,车轮跳动过程中前束角、主销内倾角、主销后倾角和车轮外倾角的变化量均有所减小。而由图12可见,优化后车轮跳动过程中轮距的变化也稍有减小,且在允许的范围内。总体而言,通过对前悬架的优化,整车的操纵稳定性能得到一定的改善。
6 结论
本文中在前悬架动力学模型的基础上构建了设计变量和不确定变量与目标函数之间的高维近似模型,代替真实的动力学模型,在满足精度的前提下,大大减少了优化计算时间。针对不确定性转化为确定性后的双层嵌套优化问题,提出了将NSGA-II和IP-GA结合起来求解前悬架优化问题,提高了解的收敛速度和质量,节省了时间。在不确定性优化的同时,引入可靠度的概念,将其作为优化的约束条件,可以很好地保证Pareto最优解集中解的安全系数。最后,在Pareto解集中针对性地选取合适的解的优化组合,重新带入Adams中与优化前的结果进行对比,结果体现了此次不确定性多目标优化的优越性,达到了兼顾安全性和实用性的目的,具有一定的理论和工程实际意义。
[1] 陈家瑞.汽车构造(下册)[M].北京:人民交通出版社,1995.
[2] 戎晓霞.不确定优化问题的若干模型与算法研究[D].济南:山东大学,2005.
[3] 吴崇辉.某清扫车车架结构分析及相关问题研究[D].长沙:湖南大学,2011.
[4] Wieslaw B, Pawel D, Tadeusz N, et al. Application of Composites to Impact Energy Absorption[J]. Computational Materials Science,2011,50:1233-1237.
[5] Lee H W, Lee G A, Yoon D J, et al. Optimization of Design Parameters Using a Response Surface Method in a Cold Cross-wedge Rolling[J]. Journal of Materials Processing Technology,2008,201:112-117.
[6] 崔胜民,余群.汽车轮胎行驶性能与测试[M].北京:机械工业出版社,1995.
[7] 郭孔辉,刘青.稳态条件下用于车辆动力学分析的轮胎模型[J].汽车工程,1998,20(3):129-134.
[8] 姜潮.基于区间的不确定性优化理论与算法[D].长沙:湖南大学,2008.
[9] 赵子衡,韩旭,姜潮.基于近似模型的非线性区间数优化方法及其应用[J].计算力学学报,2010,27(3):451-456.
[10] Sobol I M. Sensitivity Estimates for Nonlinear Mathematical Models[J]. Mathematical Modeling and Computational Experiment,1993,1(4):407-414.
[11] Shan Songqing, Wang G Gary. Metamodeling for High Dimensional Simulation-based Design Problems[J]. Journal of Mechanical Design,2010,132(5):1-36.
[12] Moore R E. Methods and Applications of Interval Analysis[M]. London: Prentice-Hall Inc,1979.
[13] Li G, Wang S W, Rosenthal C, et al. High Dimensional Model Representations Generated from Low Dimensional Data Samples. I.mp-Cut-HDMR[J]. Journal of Mathematical Chemistry,2001,30(1):1-30.
[14] Rabitz H, Al1sö F. General Foundations of High-dimensional Model Representations[J]. Journal of Mathematical Chemistry,1999,3(25):197-233.
[15] Konak A, Coit D W, Smith A E. Multi-objective Optimization Using Genetic Algorithms: A Tutorial[J]. Reliability Engineering and System Safety,2006,91:992-1007.
[16] Sardinas R Q, Santana M R, Brindis E A. Genetic Algorithm-based Multi-objective Optimization of Cutting Parameters in Turning Processes[J]. Engineering Applications of Artificial Intelligence,2006,191:127-133.
[17] Deb K, Pratap A, Agarwal S, et al. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-II[R]. Kanpur: Indian Institute of Technology, Kan GAL Report 2001,2000,6(2):182-197.
[18] Gianluca D, Serge B. Approximation Methods for Thin Plate Spline Mappings and Principal Warps[C]. Lecture Notes in Computer Science,2002:21-31.
[19] 陈栋华,靳晓雄.轮胎刚度和阻尼非线性模型的解析研究[J].中国工程机械学报,2004,2(4):408-412.
[20] 戴君.基于四分之一车辆模型的具有随机结构参数车辆的随机动力分析[J].振动与冲击,2010,29(6):211-215.
Multi-objective Reliability Optimization of Front SuspensionBased on Interval Uncertainty
Zhang Baozhen, Amir & Xiao Sijun
HunanUniversity,StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,Changsha410082
In order to reduce the change of alignment parameters of suspension in the process of wheel bouncing and hence improve the handling stability of vehicle and reduce tire wear, a multi-objective uncertainty optimization scheme for front suspension is proposed with consideration of the effects of uncertainty. Firstly a MacPherson front suspension model for a car is built with Adams/Car and a sensitivity analysis on the design hard-point parameters of suspension is conducted by using Adams/Insight. Then an approximate model between design variables, uncertain variables and objective functions is constructed by utilizing the technique of high dimensional model representation based on thin plate spline interpolation. Finally double-nested IP-GA and modified NSGA-II are applied to perform multi-objective uncertainty optimization and reliability optimization on the approximate model built with Pareto optimal solution set obtained. The results show that after optimization the changes of most alignment parameters of suspension in the process of wheel bouncing are reduced to different extents, meaning certain improvement in vehicle handling stability.
suspension; uncertainty optimization; high dimensional model representation; multi-objective optimization; reliability optimization; genetic algorithm
*教育部长江学者与创新团队发展计划项目(531105050037)和国家高技术研究发展计划(863计划)项目(2012AA111802)资助。
原稿收到日期为2013年10月8日,修改稿收到日期为2014年1月3日。

