滑模观测器和比例积分的超机动动态逆控制

潘正伟， 薛雅丽， 章鸿翔

(南京航空航天大学自动化学院，南京 210016)

0 引言

超机动飞机是指具备大迎角过失速机动能力的飞机。当飞机进行过失速机动时，迎角和角速率的变化剧烈，气动力和气动力矩均进入非线性范围，飞机的动力学特性呈现出强耦合、强非线性的特点［1］，同时也容易受到外界干扰。此时，飞机常规气动舵面操纵效率明显不足，而推力矢量技术能有效解决这个问题，甚至在恶劣条件下取代气动力。采用推力矢量技术的战机具备超机动性能，可以扭转不利的空战态势，变被动为主动，提高空战能力［2］。

未来空战多将进入大迎角、非线性飞行，线性控制器很难对超出受限包线的超机动飞行进行有效控制，因此，应用非线性控制设计控制律变得势在必行。动态逆作为经典的反馈线性化方法，在非线性系统中应用广泛，其缺点是对模型误差十分敏感;文献［2］从4个方面介绍了推力矢量控制的应用和性能;文献［3 -4］在带推力矢量的飞机上基于动态逆设计控制律;文献［5］提出了一种新的自适应模糊滑模控制方法改进传统的积分滑模面;文献［6］将滑模控制与预测控制结合，设计近空间飞行器的姿态制导律。

本文设计了具有推力矢量技术的超机动飞机基于Super-twisting 算法［7］的滑模观测器和比例积分的动态逆控制器。飞控系统被分为内外环快慢回路:快回路中针对干扰力矩采用Super-twisting 算法的滑模观测器对其估计进而设计补偿控制律;慢回路中针对系统存在的逆误差采用比例积分控制进行补偿;最后用大迎角下的“眼镜蛇”机动这种典型的过失速机动进行仿真，校验飞行控制系统的快速性和稳定性。

1 超机动飞机动态特性分析

本文以某战斗机为研究对象，该机为带矢量喷管、单垂尾、翼身融合、腹部进气道的结构布局，本文中其模型的相关数据来源于文献［8］。该型战斗机运动学方程组为

式中:V 为战斗机的飞行速度，沿机体轴可表示为V =iu+jv+kw;α 为战机的迎角;β 为战机的侧滑角;φ 为战机的滚转角。

式中:战机角速度w 沿机体轴可表示为w =ip +jq +kr，其中，p 为滚转角速率，q 为俯仰角速率，r 为偏航角速率为空气动力力矩;mT，nT为推力矢量产生的俯仰、偏航力矩;hE为引擎角动量;方程组确定了状态向量x=(α，β，φ，p，q，r)T与控制输入向量u =(δa，δe，δr，δy，δz)T之间的非线性函数关系。

空气动力力矩的L-，M-，N-可表示为

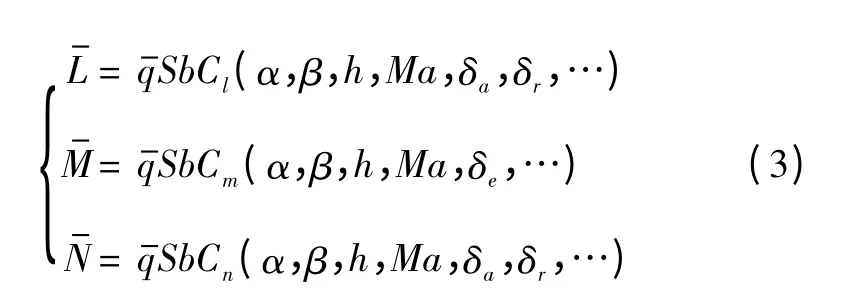
2 发动机及推力矢量模型

发动机的特性不仅随着油门指令变化，而且还与高度、马赫数、迎角、侧滑角等相关。选用风扇涡轮喷气式发动机提供动力，建模时应充分考虑节流阀调定和发动机功率水平的滞后［9］。

推力矢量技术日渐成为飞机超机动飞行的重要保障，矢量喷管使得推力T 沿机体轴3 个方向的推力分量可近似表达为

式中，δy，δz分别为发动机的侧向和纵向推力偏离发动机轴线的偏转角，偏转范围在±15°之间。受力分析后可知本文发动机的推力分量Tx与其轴线相同，不产生滚转力矩lT;推力分量Ty会对飞机产生偏航力矩nT;纵向推力分量Tz使飞机产生俯仰力矩mT。

推力矢量发动机产生的俯仰和偏航力矩为

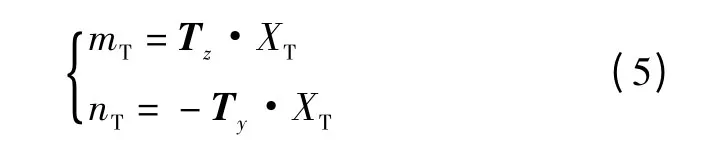
式中，XT为发动机喷口到飞机质心的距离，飞机质心位于喷口之前时XT为正。综上，飞机数学模型中的3 个轴上的总力矩可分别表示为l

3 控制器设计

非线性动态逆方法是基于非线性对象进行控制的一种方法［10］，其实质是通过非线性状态反馈和控制矩阵求逆的方法将原仿射非线性系统等效转换成线性解耦结构，从而可以采用常规的线性系统设计思路进行控制系统设计［11］。战斗机的非线性系统函数一般可表示为

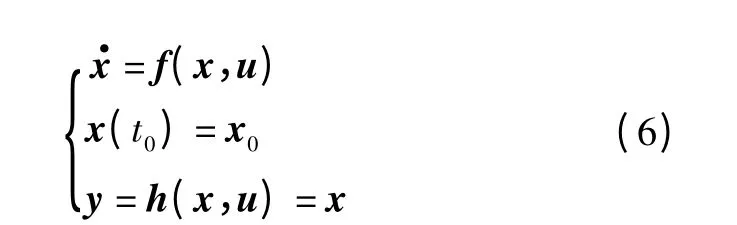
式中:f(x，u)和h(x，u)为两个非线性矢量函数;x，u，y 分别为系统的状态变量、控制变量和输出变量，x =(x1，x2)= ((α，β，φ)，(p，q，r))T，u = (δa，δe，δr，δy，δz)T。利用奇异摄动理论将状态变量分组，x1=(α，β，φ)T为飞机相对于机体轴的姿态矢量，是大迎角机动控制与增稳所必需的［12］，作为外环慢控制变量，x2=(p，q，r)T为转动角速度矢量，对增加飞机转动阻尼非常重要，控制舵面的偏转，作为内环快控制变量。一般内外环选取不同的带宽，保证其运行在不同的时间域。令=v，若g(x)可逆，则v =wk(xc-x)，此时系统变为一阶多变量线性解耦结构。wk为对角阵，表示系统的带宽。图1 为控制结构图。

图1 推力矢量下超机动飞机动态逆控制结构图Fig．1 Dynamic inversion control structure of supermaneuverable aircraft with thrust vectoring

3．1 快回路基于Super-twisting 算法滑模观测器动态逆控制律设计

快回路动力学方程为

式中:ff(x2)为非线性耦合力矩;gf(x2)u 为舵面产生的操纵力矩，u = (δa，δe，δr，δy，δz)T;控制分配矩阵为

令快变量动力学系统的期望为一阶环节，即

式中:下标c 表示指令值;下标d 表示期望值;输入pc，qc，rc为外环慢回路的输出;带宽wp，wq，wr的数值取10 rad/s，3 个带宽的值相等有利于协调控制减小侧滑。

应用动态逆可得内环快回路标称控制律为

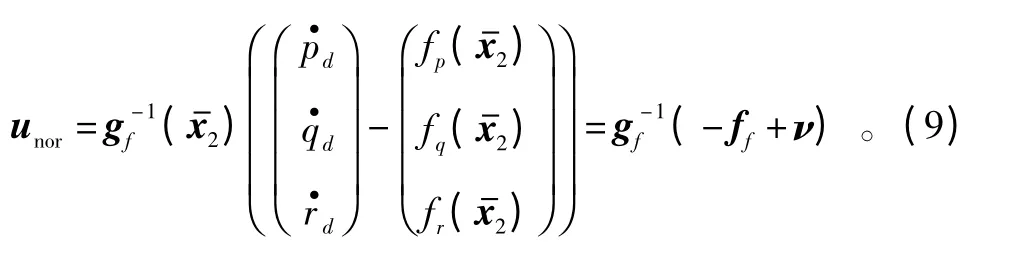
理论上，基于动态逆-比例积分方法设计的控制器可以完成机动动作，且有较好的稳定性。但是，实际上飞机的建模不可能完全准确，且超机动飞行也易受到外界的干扰，需要对干扰进行抑制，提高系统的鲁棒性。针对飞机姿态角速度通道受到外界飞行环境的直接力矩干扰，引入非线性滑模观测器［13］来估计系统的干扰，进而产生补偿控制律，抑制力矩干扰。飞机受干扰下的非线性模型为

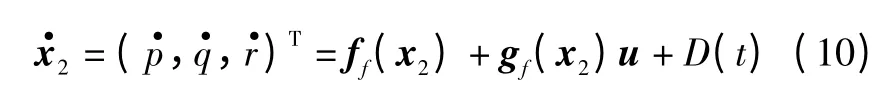
图2 快回路控制结构图Fig．2 Structure of fast loop control

干扰情况下，为了设计滑模观测器，给出如下假设。

假设1 系统所有状态可观测。

假设2 干扰D 关于时间的偏导数是连续且有界的，且存在已知的有界常数C ＞0 使成立。

引理1 给定如下受扰非线性微分方程［14］

对于多输入多输出系统，设计基于Super-twisting算法的滑模观测器，表达式为

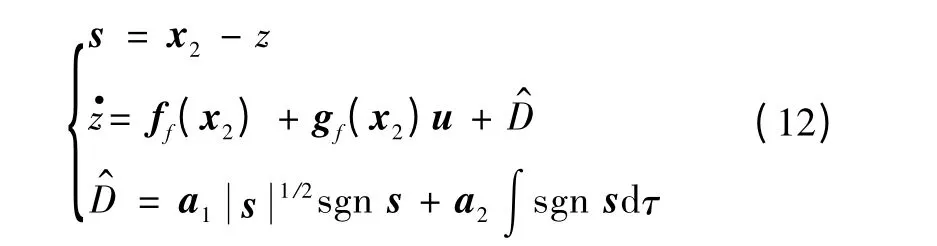
式中:s∈Rn，为辅助滑模向量;，为滑模控制量，在表达式中

该组的主要职责：负责组织专业抢险应急分队对紧急重大险情开展应急抢险、伤员救治，组织救援分队对灾害地区开展应急救援，保障水、电、路、通信等基础设施畅通。

定理1 当干扰导数有界时选取适当的参数矩阵a1，a2，干扰观测值可一致收敛到真值D。

定理1 给出以下证明。

定理2 内环快回路力矩干扰下引入Super-twisting 算法滑模观测器后，系统渐近稳定。

定理2 给出以下证明。

3．2 慢回路基于比例积分的动态逆控制律设计

慢回路状态动力学方程为

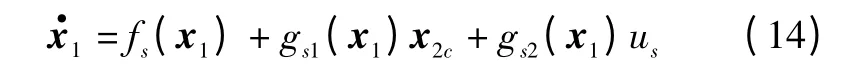
式中:fs(x1)表示飞机非线性耦合力;gs1(x1)x2c表示与的运动学关系;gs2(x1)us表示舵面产生的操纵力。舵面偏转产生的操纵力比操纵力矩小得多，如果考虑舵面偏转产生的操纵力，那么模型的状态方程会产生非最小相位问题，这样设计的控制律将会导致控制系统内部状态的不稳定。因此，设计控制律时一般忽略舵面产生的操纵力，进而动态方程为

式中，带宽wα，wβ，wφ的数值取2 rad/s，应用动态逆可得外环慢回路的控制律为

由于慢回路中存在由非线性对消引起的系统逆误差，因此将慢回路动态逆控制与比例积分控制相结合来完善控制律［16］。在慢回路中引入(的积分，当存在非线性对消误差或者干扰产生的稳态误差时，，将其误差的积分反馈到回路中，增加一个附加反馈，可有效消除其影响，提高系统的鲁棒性。因为慢回路包含被忽略的快回路响应在内，引入比例积分控制对快回路的改善没有对慢回路的改善明显，所以比例积分控制一般只需要在慢回路系统中引入。

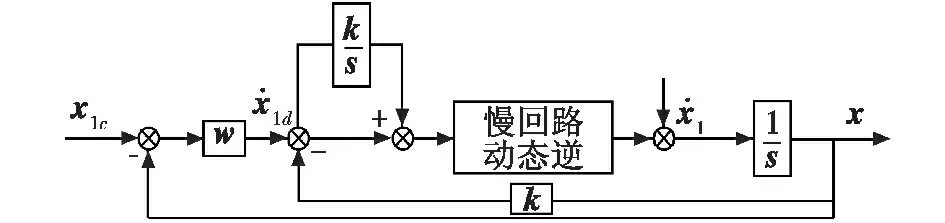
图3 慢回路控制结构图Fig．3 Structure of slow loop control

整理后可以得出最终慢回路控制律为

式中:k 为对角阵，对角元素值大小为0．5 rad/s;ws为对角阵，对角元素值为wα，wβ，wφ。

4 “眼镜蛇”机动仿真校验

“眼镜蛇”机动是飞机大迎角下典型的过失速机动［17］，运用指令生成器生成机动指令，仿真时间设为10 s。

超机动飞机初始状态:x0=y0=0 m，h0=3000 m;V0=125 m/s，θ0=ψ0=0°;α0=5°，β0=φ0=0°;p0=q0=r0=0 (°)/s;δa0=δc0=δr0=δy0=δz0=0°;δth=0．7。干扰力矩为d1=2×103sin(πt)N·m，d2=8×103sin(πt)N·m，d3=1．5 ×103sin(πt)N·m;经调试，式(13)中a1=diag(120，240，110)，a2= diag(7000，280000，5200)。仿真曲线如图4 所示。

图4 中，飞行迎角α 最大值为68．29°，远远超过一般飞机在常规机动中的最大限制迎角30°，是典型的大迎角过失速机动飞行。侧滑角和滚转角基本无变化，稳定在0°上下，说明在整个大迎角机动过程中，飞机保持了无侧滑、无滚转飞行。滚转角速率p 和s 偏航角速率r 基本为0，俯仰角速率q 变化明显，3 个角速率的变化说明了飞机基本保持了良好的航向稳定及滚转稳定。X，Y，H 的三维仿真图表明在“眼镜蛇”机动中飞机高度并没有大的变化，航向基本保持不变，符合实际情况。飞行速度V 在机动过程中随着迎角的增大急剧降低，进入过失速区，最小值达到了55．41 m/s。6 s 后随着机动结束，速度慢慢增大，返回初始值。机动中飞机横侧向通道内的δa，δr，δy3 个偏转角的偏转角度都不大;而纵向通道的δe，δz2 个偏转角协调工作，偏转角度都在各自偏转范围内且无舵面满偏的现象。由图4 中的仿真曲线结合飞机操纵特性和实际情况可知，飞机在外部直接力矩干扰下各参数变化的过程合理，有效地跟踪飞行指令实现了“眼镜蛇”机动动作，飞行控制系统具有较好的快速性、稳定性。

图4 “眼镜蛇”机动仿真图Fig．4 Cobra maneuver simulation

5 结论

本文通过分析推力矢量下的飞机非线性模型，研究了基于Super-twisting 算法的滑模观测器和比例积分控制的非线性动态逆控制方法，由设计的控制律产生驱动舵面偏转的控制信号。考虑到实际飞行中存在直接干扰力矩，在内环快回路动态逆控制中加入针对干扰力矩的滑模观测器，进而设计补偿控制律，抑制外部力矩干扰。针对外环慢回路存在系统逆误差，引入经典比例积分控制进行补偿，完善慢回路动态逆控制律。对飞机进行大迎角下“眼镜蛇”机动仿真的结果表明，本文设计的控制器具有良好的动力学响应，飞行控制系统在短时间内准确地跟踪控制指令完成过失速机动，具有较好的快速性和稳定性。

［1］ 焦裕松，谢蓉，王新民，等． 超机动飞机的动态建模与控制律设计及仿真［J］．控制与决策，2010，25(5):744-747．(JIAO Y S，XIE R，WANG X M，et al． Dynamic modeling and control law design for a supermaneuverable aircraft［J］． Control and Decision，2010，25(5):744-747．)

［2］ 肖宇，张兴有．战斗机发动机推力矢量控制技术的应用［J］．航空发动机，2008，34(4):56-58．(XIAO Y，ZHANG X Y． The application of flight engine trust vector control technology［J］．Aeroengine，2008，34(4):56-58．)

［3］ 刘凯，朱纪洪，余波．推力矢量飞机纵向鲁棒动态逆控制［J］．控制与决策，2013，28(7):1113-1116．(LIU K，ZHU J H，YU B．Longitudinal control of aircraft with thrust vectoring using robust dynamic inversion［J］．Control and Decision，2013，28(7):1113-1116．)

［4］ 王文娟，马洪忠，刘长林． 无人机综合飞行/推力矢量控制［J］．航空学报，2008，29(s):150-155． (WANG W J，MA H Z，LIU C L．Integrated flight/vectored thrust control for UAV［J］． Acta Aeronautica et Astronautica Sinica，2008，29(s):150-155．)

［5］ 刘鑫燕，王玉惠，吴庆宪．方向未知的非仿射非线性系统的模糊滑模控制［J］． 吉林大学学报:信息科学版，2014，32(2):145-150． (LIU X Y，WANG Y H，WU Q X． Fuzzy sliding mode control for a class of non-affine non-linear systems with unknown control direction［J］．Journal of Jilin University:Information Science Edition，2014，32(2):145-150．)

［6］ 程路，姜长生，都延丽，等． 基于滑模干扰观测器的近空间飞行器非线性广义预测控制［J］． 宇航学报，2010，31(2):423-430． (CHENG L，JIANG C S，DU Y L，et al． The research of SMDO based NGPC method for NSV control system［J］．Journal of Astronautics，2010，31(2):423-430．)

［7］ LEVANT A． Slidingorder and sliding accuracy in sliding mode control［J］． International Journal of Control，1993，58(6):1247-1263．

［8］ GILBERT W P，NGUYEN L T，VAN GUNST R W．Simulator study of the effectiveness of an automatic control system designed to improve the high-angle-of-attack charactaristics of a flighter airplane［R］． Virginia:Langley Research Center，1976．

［9］ ATESOGLU Ö，ÖZGÖREN K．High-α flight maneuverability enhancement of a twin engine flight-bomber aircraft for air combat superiority using thrust-vectoring control［C］//AIAA Guidance，Navigation，and Control Conference，Colorado:AIAA，2006-6050．

［10］ SNELL S A，ENNS D F，ARRARD W L． Nonlinear dynamic-inversion flight control of supermaneuverable aircraft［D］．Minnesota:University of Minnesota，1991．

［11］ BUGAJSKI D J，ENNS D F． Nonlinear control law with application to high angle-of-attack flight［J］． Journal of Guidance，Control，And Dynamic，1992，15(3):761-767．

［12］ 陈永亮．飞机大迎角非线性动力学特性分析与控制［D］．南京:南京航空航天大学，2007． (CHEN Y L．Large angle of attack aircraft nonlinear dynamic analysis and control［D］．Nanjing:Nanjing University of Aeronautics and Astronautics，2007．)

［13］ 刘金琨．滑模变结构控制MATLAB 仿真［M］．2 版．北京:清华大学出版社，2012．(LIU J K．The sliding mode variable structure control and MATLAB simulation［M］．2nd ed．Beijing:Tsinghua University Press，2012．)

［14］ SHTESSEL Y，TOURNES C，KRUPP D．Reusable launch vehicle control in sliding modes［C］//AIAA Guidance，Navigation，and Control Conference，New Orleans:AIAA，1997:335-345．

［15］ LEVANT A．Higher-order sliding modes，differentiation and output-feedback control［J］． International Journal of Control，2003，76(9):924-941．

［16］ 谢蓉，王新民，李俨．超机动飞机动态逆-PID 控制器设计［J］．飞行力学，2009，27(2):63-66．(XIE R，WANG X M，LI Y．Dynamic inversion-PID controller of a supermaneuverable aircraft［J］．Flight Dynamics，2009，27(2):63-66．)

［17］ 叶茂林，申功璋．新一代战斗机机动作战决策与仿真［J］．北京航空航天大学学报，2003，29(4):358-361．(YE M L，SHEN G Z．Super-maneuverable combat decision-making and simulation for a fighter［J］． Journal of Beijing University of Aeronautics and Astronautics，2003，29(4):358-361．)