城市公交系统的最优路径搜索算法

邓 竞 伟

(西北民族大学数学与计算机科学学院，甘肃 兰州，730124)



城市公交系统的最优路径搜索算法

邓 竞 伟

(西北民族大学数学与计算机科学学院，甘肃 兰州，730124)

在分析城市公交系统特点的基础上，利用改进的最短路径算法对此问题进行阐述和分析，描述了Dijkstra算法和改进的最短路径算法，并将改进的算法应用于城市公交系统中，最后用一个简单的例子进行验证。结果表明，在搜索效率上改进后的算法比Dijkstra算法好。

Dijkstra算法；城市公交网络；最优路径

随着城市建设的飞速发展以及城市公交系统的不断完善，公交车已成为城市居民出行的主要交通工具[1]。公交系统是城市交通系统的一个重要组成部分，最优线路的选择不仅是公交公司一直面临的问题，也是乘客出行时关注的首要问题。能够很好地解决城市拥堵的方法是大力发展公交，提高乘坐公交出行人数的比例，实现这一目标的最好方法是乘坐公交的出行效率提高，减少乘坐公交的出行时间[2]。由于从一个地点到达另一个地点可能会有许多线路选择，为了选择一条最佳线路，对乘客的出行时间和费用有着至关重要的作用，也就是说，总体考虑了距离、时间、费用等问题，此类现实问题关系到如何求解最短路径问题。最短路径是人们一直关注的问题[3]，目前最短路径的实际应用仍是一个研究热点[4]。有许多研究领域，如网络分析、交通规划、通信等起着重要作用[5]。

1 城市公交网络

1.1 公交网络的特点

在公交网络中[6]，不同线路在行程上有着相同的公交站点，即在不同线路上会经过相同的站点，但在公交站点分布的实际情况中，即使是同一个站点也会存在空间位置上的不同，若将一个公交站点看作一个节点，对网络进行分析时，需要把不同线路的公交站点抽象为一个节点，只有这样才能模拟出不同公交线路之间的乘客可换车情况的网络。

1.2 公交网络最短路径

公交网络中的一个关键问题是最优路径的选择，最优路径是计算2点间的距离最短，城市公交线路最佳选择问题可以描述为：某乘客从起点S出发前往目的地E，S与E之间存在多条可供乘坐的线路，并且这些线路和经过线路的公交站点组成了一个公交网络图。为了乘客出行方便，在研究网络模型和最短路径算法时，首先要了解公交乘客出行时所考虑的因素，通过对公交乘客出行心理行为的研究来确定模型的优化目标，通常乘客出行会从以下几个方面考虑[7]：换车次数、时间、费用、距离等，乘客满意度一般有两种形式：一个是总出行时间，另一个是乘客的出行总成本[8]。

2 公交网络数学模型的建立

为了考虑公交乘客出行时间和费用最少等问题时，只需将研究问题中的一些参数做一些调整后，这些考虑的问题将会是最短路径问题。

城市公交网络是由线路和站点组成，可以抽象成一个网络拓扑图G=[6](其中，V——顶点集，E——边集，L——边权值)。

3 传统的最短路径算法

目前，求解最短路径问题算法很多[9]，Dijkstra算法[10]仍然是公交网络最短路径算法的首选算法，但是在求解时都有可能会搜索所有的网络节点，在网络节点多时，此算法的时间花费增长速度很快，很难满足实际运算的需要[11]。

Dijkstra算法的核心过程[12]是将满足条件的T(临时标号)节点变成P(固定标号)节点，即计算每一步是把某个点的T标号变成P标号，这样一旦终点到达P节点，计算就结束。

Dijkstra算法具体步骤描述如下[6]：

(1)给起点pi标上P标号，给其他各点标上临时标号。

(2)在所有临时标号中取最小值，则把该点的临时标号改为固定标号。

(3)重新计算具有临时标号的其他各点标号：选择临时标号中的较小者作为新标号。

(4)重复上述步骤，当算法结束时，从pi到pm的最短路径的长度由标号的终值给出，这时d(pm)就是从pi到pm的最短路径。

4 改进搜索算法

在城市公交网络中，最短路径是一种网络优化问题[13]。Dijkstra算法是用来求解图上任一节点到其余各个节点的最短路径，采用邻接矩阵存储网络拓扑结构，随着节点数的增加，其计算效率和存储效率越低[14]。尤其在站点和线路相对多的情况下，在实际应用中，使用Dijkstra算法耗费大量的计算时间[15]，即当网络模型中节点和边数较多时，算法的计算量很大，时间花费相对多，成为应用Dijkstra算法的瓶颈[16～18]。

通过分析Dijkstra算法的不足，为了提高效率，考虑将最短路径问题分解成2个子问题，即分别为由起点到终点和由终点到起点求解最短路径的两个问题，两个问题并行处理，从2个站点同时搜索，到交叉时就可从2个站点都找到到达同一站点的最短路径，然后再从结果中找出最短路径，把搜索到的下一个站点放到一个集合里，从而大幅度减少搜索时间。

5 实 例

一个简单的公交网络带权图如图1所示，图中共有7个站点，15条线路。应用上述算法计算公交乘客从起点S到终点E的最短路径，图中的每个顶点表示站点，边表示2个站点之间的线路，边上的权值表示2个站点之间的距离、途中所经过的时间或者是交通费用等，此时路径长度是路径上边的权之和[19]。例如，从A点到B点，A点高于B点，考虑上坡下坡的车速不同，则有向边和上表示行使时间的权值也不同，所以交通网络属于有向网。假设某乘客从起点S出发前往终点E，其间有多条线路可供选择，两点之间线路的权值表示该线路的线程，权值越大说明距离越长，反之则距离越短。

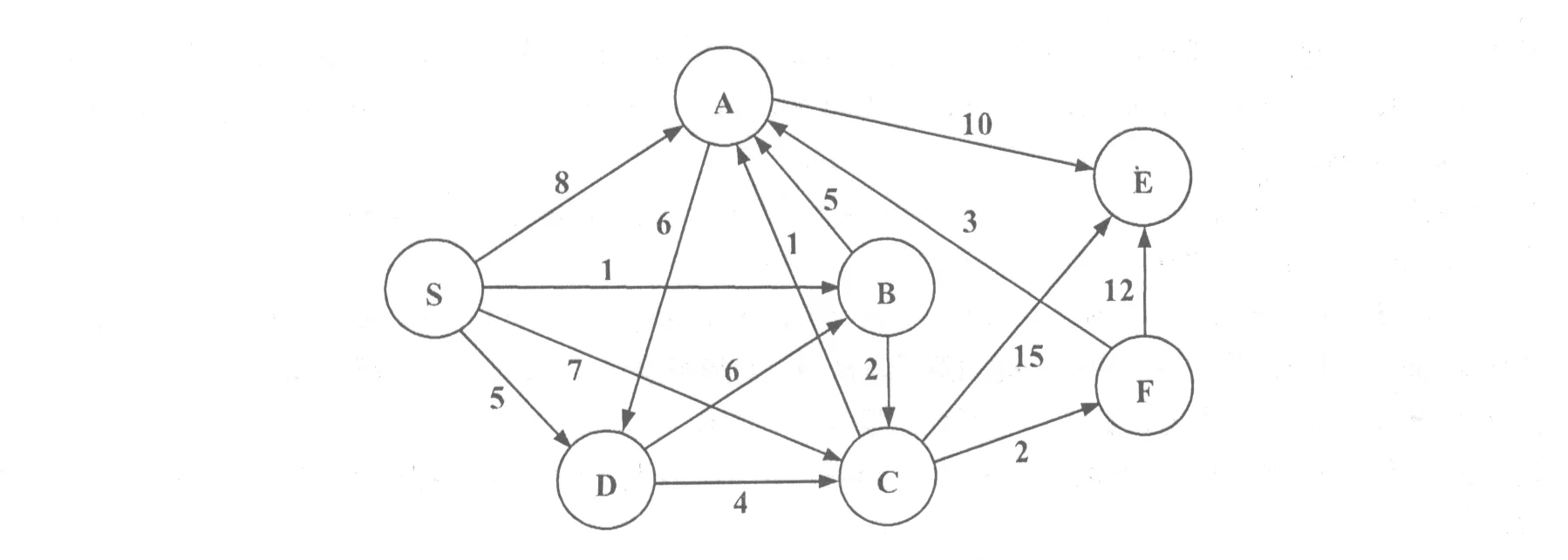
图1 公交网络带权简图

各条线路的线程见表1。

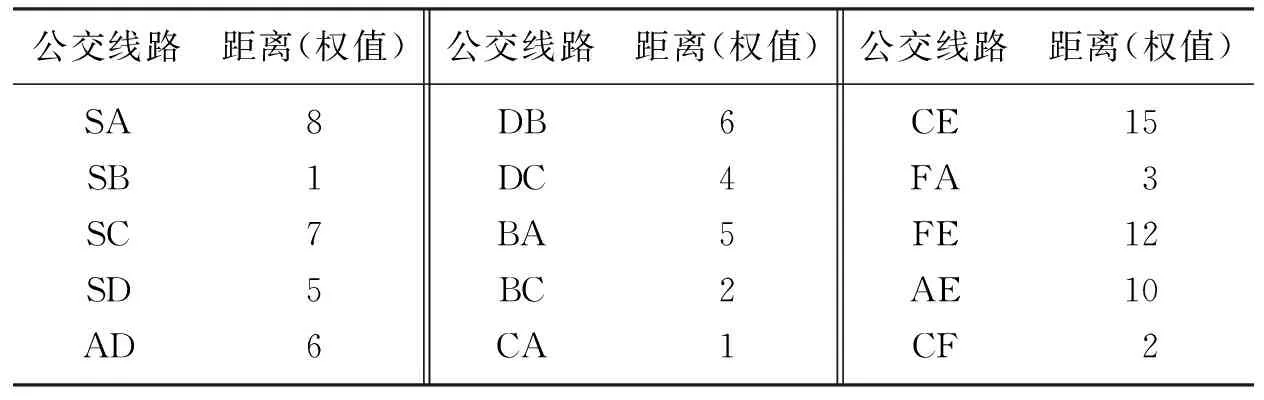
表1 公交网络带权简图中的线路及距离

Dijkstra算法和改进后的算法具体搜索过程分别见表2，表3。

表2 Dijkstra算法对公交网络带权简图中的最短路径的具体搜索过程

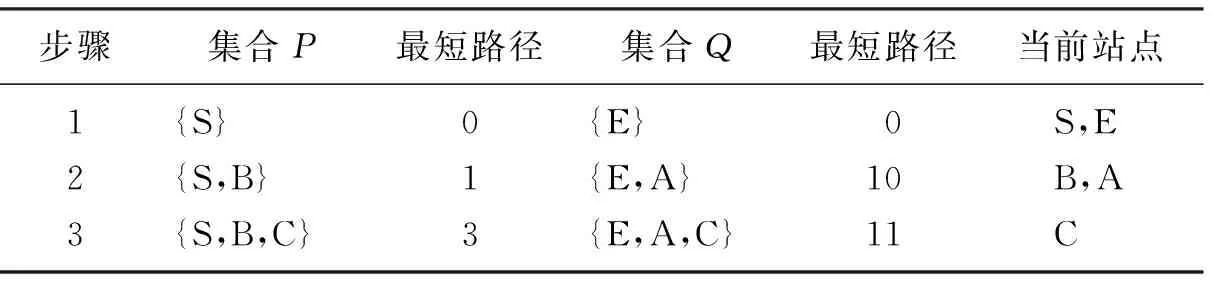
表3 改进后的算法对公交网络带权简图中的最短路径的具体搜索过程

从表2，表3中可以看出，从起点S到终点E的最短线路是相同的，对于站点和线路少此算法不明显，但是对于目前城市公交系统中站点多、线路多、道路拥堵等特点来看，改进后的算法效率大幅度提高。

6 结 论

通过分析公交系统的特点以及乘客的需求，描述了Dijkstra算法，根据实例分析，对已有算法和改进的算法进行比较，验证了在城市公交系统中，尤其是节点和线路较多时，改进的算法可以有效提高效率，以此方便乘客出行。

[1] 梁虹，袁小群，刘蕊.一种新的公交数据模型与公交查询系统实现[J].计算机工程与应用，2007，43(3):234-238.

[2] Zhan F B.Three Shortest Path Algorithms on Real Road Networks:Date structure and procedures[J].Journal of Geographic Information and Decision Analysis,1997，1(1):69-82.

[3] Xu M H，Liu Y Q，Huang Q L，et al.An improved Dijkstra’s shortest path algorithm for sparse network[J].Applied Mathematics and Computation,2007,185(1)：247-254.

[4] T Takaoka.Shortest path algorithms for nearly acyclic directed graphs[J].Theor Comput Sci,1998(203):143-150.

[5] 谭国真，高文.时间依赖的网络中最小时间路径算法[J].计算机学报，2002，25(2):165-172.

[6] 龙光正，杨建军.改进的最短路算法[J].系统工程与电子技术，2002，24(6):106-108.

[7] 杨新苗，王炜，马文腾.基于GIS的公交乘客出行路径选择模型[J].东南大学学报:自然科学版，2000，30(6):87-91.

[8] 何胜学，范炳全.公交网络最优路径求解算法[J].交通运输工程与信息学报，2007，5(1):22-27.

[9] 周培德.交通道路网中任意两点之间最短路径的快速算法[J].计算机工程与科学，2002, 24(4)：35-37.

[10] Bondy J A，Murty U S R.Graph Theory with Applications[M].London: The Macmillan Press Ltd，1976.

[11] 严寒冰，刘迎春.基于GIS的城市道路网最短路径算法探讨[J].计算机学报，2000，23(2)：210-215.

[12] 王元彪.智能交通系统中Dijkstra算法的高效实现[J].计算机工程，2007，33(6):256-258,261.

[13] Cantone D，Faro S.Two-Levels-Greedy:a generalization of Dijkstra’s shortest path algorithm[J].Electronic Notes in Discrete Mathematics,2004,17(20):81-86.

[14] 章永龙.Dijkstra最短路径算法优化[J].南昌工程学院学报，2006，25(3)：30-33.

[15] 余冬梅，张秋余，马少林，等.Dijkstra算法的优化[J].计算机工程，2004，30(22):145-146.

[16] 鲍培明.距离寻优中Dijkstra算法的优化[J].计算机研究与发展,2001，38(3):307-311.

[17] 刘彦良，王鹏涛.复杂网络的优化模型及最短路径求解[J].天津理工大学学报，2006，22(1)：33-35.

[18] Han Y J.A note of an O(n3/logn) time algorithm for all pairs shortest paths[J].Information Processing Letters，2008,105(3)：114-116.

[19] 张鑫，刘岳峰，郑江华，等.针对公交的最优路径算法[J].计算机工程与应用，2006(22):207-209.

(责任编辑：朱宝昌)

The Optimal Path Searching Algorithm of Urban Public Traffic Systems

DENG Jing-wei

(School of Mathematics and Computer Science，Northwest University for Nationalities，
Gansu Lanzhou，730124，China)

Based on the analysis of the characteristics of urban public transport system, we used the shortest path algorithm to carry on the elaboration and the analysis, then described the shortest path algorithm and improved Dijkstra algorithm. The improved algorithm was applied to the urban public transportation system and finally verified by a simple example. The results showed that the improved algorithm is efficiently better than the Dijkstra algorithm in searching function.

Dijkstra algorithm; urban public traffic network; optimal path

10.3969/J.ISSN.1672-7983.2015.02.014

教育部人文社会科学研究青年基金项目(项目编号：13YJCZH029;12YJCZH027)；中央高校基本科研业务费专项资金项目(项目编号：31920150039)。

2015-04-21; 修改稿收到日期: 2015-05-24

U491.17

A

1672-7983(2015)02-0066-04

邓竞伟(1980-)，女，讲师，硕士。主要研究方向：复杂网络、信息处理。