一类非线性R-L分数阶积分微分方程的数值解法

张盼盼,任正杰

(1 宁夏大学数学计算机学院,宁夏 银川，750021；2 甘肃省永昌县第一高级中学)



一类非线性R-L分数阶积分微分方程的数值解法

张盼盼1,2,任正杰2

(1 宁夏大学数学计算机学院,宁夏 银川，750021；2 甘肃省永昌县第一高级中学)

利用Adomian多项式将分数阶积分微分方程中的积分项离散化,进而得到原方程解的级数表达形式,数值算例验证了该分解方法的有效性。

Adomian多项式;分数阶积分微分方程;数值解

分数阶微积分是一古老而新鲜的概念。早在17世纪末,就有像L’Hospital,Leibniz等数学家开始考虑分数阶微积分,但由于缺乏应用等众多原因的支撑,使得分数阶微积分的发展相对滞后。近年来,越来越多的分数阶微积分方程广泛出现在各大工程领域。例如,PID控制理论、粘弹性材料及混沌现象等反常问题[1,2],其中有些问题建模后得到的方程大多数都是非线性分数阶积分微分方程。由于分数阶微积分复杂的定义,增加了分数阶方程的求解难度,分数阶积分微分方程的求解对众多学者来说更是挑战。目前关于分数阶积分微分方程数值解的文献已有一些,主要是用小波的方法求解 Fredholm或Volterra型的分数阶积分微分方程[3～6]。LI Huang等[7]采用Taylor级数的方式求解了线性分数阶积分微分方程。然而,关于非线性分数阶积分微分方程数值解的文献甚少。

利用Adomian分解法求解代数方程具有强大的优越性，其解为级数形式、收敛快、计算方便且容易在计算机上运算。它的核心思想是：把方程拆成n个部分，把解拆成n个项，同时非线性项用一种特殊的多项式An进行替代，然后由低阶解分量逐渐向高阶解分量逐一解出，从而得到方程的近似解析解，也可以得到精确解。该方法无需进行任何变换，很好的保持了原方程的物理性质。在实际生活中不仅会遇到线性问题和确定问题,而且经常会遇到非线性问题甚至是随机问题。对于这些非线性问题,通常的办法是将其线性化近似处理或采用扰动技术。然而,这些方法在求解时无形中改变了原问题,得到的解往往不能满足实际需要。Adomian分解法不会存在这样的问题,计算量很小，而且很快就能收敛到真解。所以,Adomian分解法是求解非线性方程的有力工具[8,9],笔者利用Adomian多项式将R-L分数阶积分微分方程离散化,得到原方程解的级数表达式,并使用数值算例证明该算法的有效性。

1 预备知识

定义[1]设f(x)∈L[a,b],α>0。则称

(1)

为Riemann-Liouville分数阶积分,其中t∈[a,b], Γ(α)为Gamma函数。

2 主要结果

设

(2)

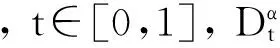
(3)

由Adomian分解法知,设

(4)

其中

将(4)式代入(3)式,整理得

(5)

(6)

(7)

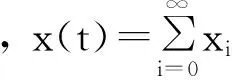
3 解的收敛性

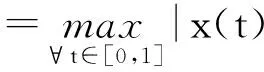
唯一性定理 方程(2)有唯一解⟺0<γ<1,其中γ=λML/Γ(α+2)。

证明:设

则有

由方程(2)的条件得

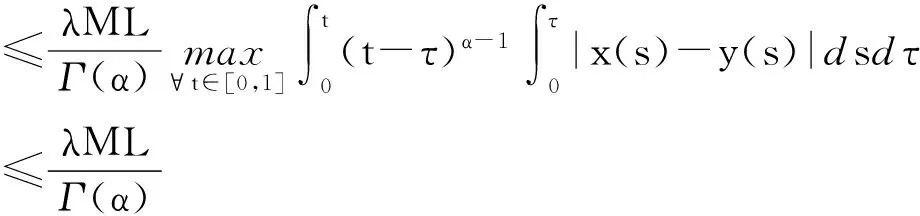
=γ‖x-y‖

易见,当γ∈(0,1)时,H即为压缩映射。由引理知,H中存在唯一的不动点,即方程(2)有唯一解。

收敛性定理 方程(2)的解收敛⟺g(t)有界且0<γ<1,其中γ=λML/Γ(α+2)。

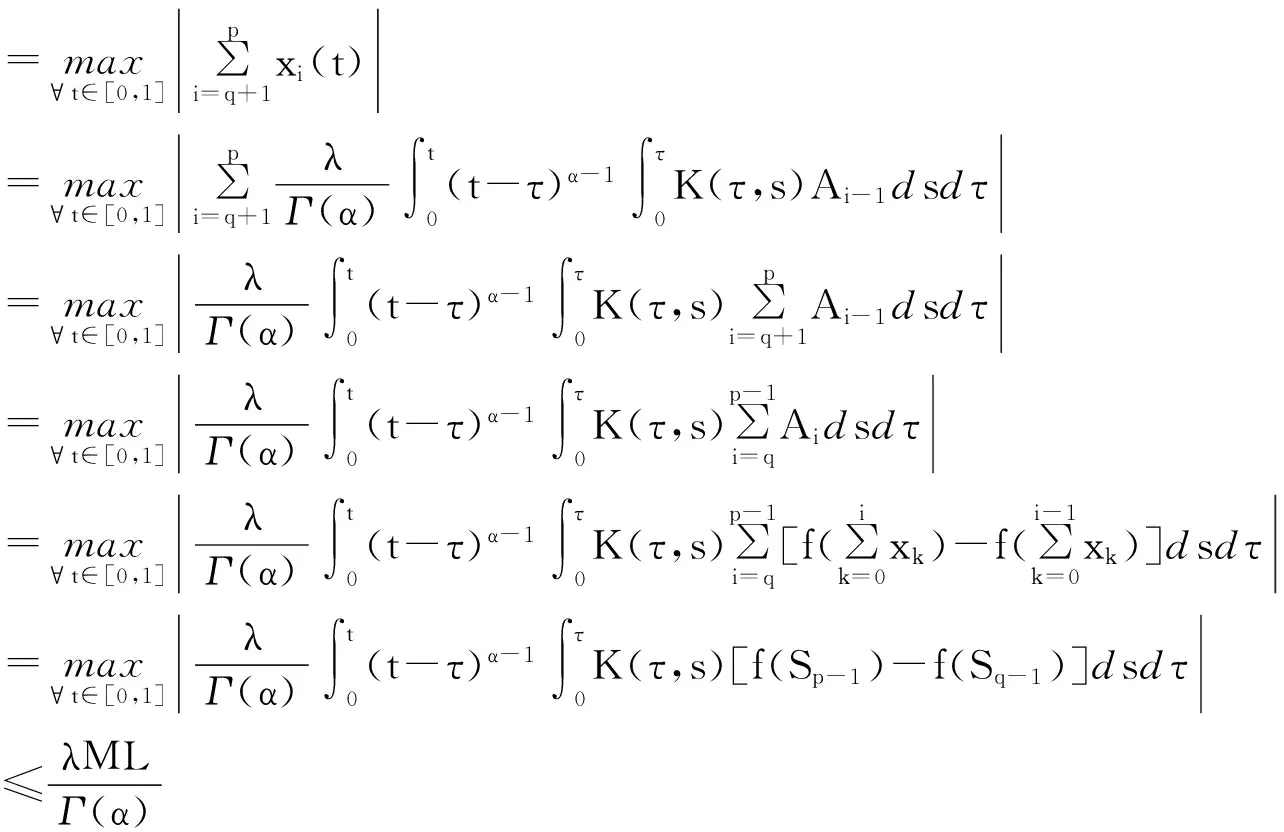
=γ‖Sp-1-Sq-1‖

所以

‖Sp-Sq‖≤γ‖Sp-1-Sq-1‖≤γ2‖Sp-2-Sq-2‖≤…≤γq‖Sp-q-S0‖

令p=q+1,则有

‖Sp-Sq‖≤γq‖S1-S0‖

‖Sp-Sq‖ =‖Sq+1-Sq+Sq+2-Sq+1+…+Sp-Sp-1‖

≤‖Sq+1-Sq‖+‖Sq+2-Sq+1‖+…+‖Sp-Sp-1‖

≤[γq+γq+1+…+γn-1]‖S1-S0‖

因为g(t)有界,由(5),(6)式知,x1(t)有界,因此当γ<1,q→∞时,‖Sp-Sq‖→0,即函数列{Sp}是Banach空间B上的柯西列。

4 数值算例

例1 求解分数阶积分微分方程

其初始条件为x(0)=1。这类方程的解析解一般不易求得,但由文献知,当α=1时,此方程的解析解为x(t)=et。因此,以α=1为例检验笔者算法的有效性。

图1 非线性R-L分数阶积分微分方程的数值解与精确解的比较

表1 非线性R-L分数阶积分微分方程的数值结果及误差(α=1)

例2 求解分数阶积分微分方程

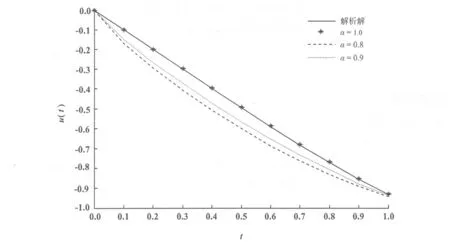
图2 分数阶积分微分方程的数值解与精确解的比较

表2 α=1时分数阶积分微分方程的当数值解与精确解的比较

[1] 陈文,孙洪广,李西成.力学与工程问题的分数阶导数建模[M].北京：科学出版社,2010.

[2] 张亚鹏,高峰.分数阶粘弹性积分本构模型[J].济南大学学报:自然科学版,2012,26(1):102-105.

[3] 尹建华,任建娅,仪明旭.Legendre小波求解非线性分数阶Fredholm积分微分方程[J].辽宁工程技术大学学报:自然科学版,2012,31(3):405-408.

[4] Xiaohua Ma,Chengming Huang.Numerical solution of fractional integro-differential equations by a hybrid collocation method[J].Applied Mathematics and Computation,2013,219(12):6 750-6 760.

[5] Mustafa Gulsu.Numerical approach for solving fractional Fredholm integro-differential Equation[J].International Journal of Computer Mathematics,2013,29(16):1-22.

[6] Zhu Li,Fan Qibin.Numerical solution of nonlinear fractional-order Volterra integro-differential equations by SCW[J].Commun nonlinear Sci Numer Simulat,2013,18(5):1 203-1 213.

[7] LI Huang,Xianfang Li.Approximate solution of Fracional integro-differential equations by Taylor expansion method[J].Computer Math Appl,2011,24(62):1 127-1 134.

[8] G Adomian.Random Volterra integra equations[J].Math Comput Model,1995,22(8):101-102.

[9] G Adomian,R Rach.Modified Adomian polynomials[J].Math Comput Model,1996,24(11):39-46.

[10] 张恭庆,林源渠.泛函分析讲义[M].北京:北京大学出版社,2011.

(责任编辑：朱宝昌)

Numerical Solution of a Class of Nonlinear R-L Fractional Integro-differential Equation

ZHANG Pan-pan1，2,REN Zheng-jie2

(1 Department of Mathematics and Computer Science,Ningxia University, Yinchuan, 750021;2 The First High School of Yongchang, Yongchang Gansu;China)

In this paper, Adomian polynomial is used to discrete fractional integro-differential equation to obtain solution of the original equation, numerical examples show that this method is effective to approximate the numerical result.

Adomian polynomials;fractional integro-differential equations;numerical solution

10.3969/J.ISSN.1672-7983.2015.02.010

2015-04-02; 修改稿收到日期: 2015-05-24

O241.8

A

1672-7983(2015)02-0047-05

张盼盼(1986-),男,硕士研究生。主要研究方向：复分析在力学中的应用。