加强思辨训练，让学生学会数学思维

江苏句容市崇明小学（212400） 陈 清

在教学中，学生由于缺乏思辨能力，面对问题往往思维摇摆，缺乏主见，甚至出现逻辑不清、言语不明的现象。为此，笔者认为，教师要多给学生提供一些思辨训练，以促进学生学会数学思维。何谓数学思辨？它是指用数学的方法和角度进行思考和辨析，其中包括逻辑思维和非逻辑思维两种，涉及数学意识、数学思考、推理、判断、表述等多种思维活动和思维过程。那么，如何进行数学思辨训练呢？

一、从小处入手，引导有序思维

良好的数学思维，有赖于良好的思维习惯和思维方式。小学生在面对问题时大多容易思维混乱。此时，教师要善加引导，带领学生从最基本、最容易解决的小问题入手，如剥笋一般层层展开，培养其有序思维的习惯，从而实现对大问题的有效解决。

例如，在教学“圆的认识”时，我先在黑板上画了一个圆，又让学生在纸上画了一个圆，然后让学生思考：同样都是圆，虽然画圆的工具和位置不同，但有什么相同之处？学生根据观察发现，这些圆都要先确定一个中心点（即圆心），并围绕这个点旋转360°，而且这中间要隔开一段距离（即半径或者直径）。通过思辨交流，学生逐步对圆的基本属性有了初步的了解。可见，通过有效的点拨和引导，学生对数学的表面问题及表象特征有了全面的认识，从而厘清了自己的思维，逐步构建有序思维的模式，使其思维水平获得提升。

二、从条件入手，引导分层思维

对学生进行思维训练，需要一个循序渐进的过程，这是教师在教学中不可忽视，也亟待重视的问题。在进行思维训练时，切忌“眉毛胡子一把抓”，而是要从条件入手，层层深入，契合学生的认知特点，由表象开始逐步过渡，一步步进入抽象复杂的数学学习中。

如在教学“分数的认识”这一课时，我让学生思考：如果将一个胡萝卜平均分给两只兔子，那么每只兔子分得多少？学生认为是一半，用分数表示就是1/2。如何理解这个1/2呢？它表示什么意思？学生认为，就是把一个桃子平均分成两份，每一份就是这个桃子的1/2。此时学生是否真的理解了分数呢？我特意又深入了一层，让学生思考：如果要将一张长方形纸对折，表示其中的1/4，你怎么弄？学生动手操作后得出结论：表示将一张纸平均分成4份，每一份就是这张纸的1/4。让学生再继续思考：要在这张长方形的纸上涂抹出3/4，怎么涂？怎么理解？学生认为，首先要将这张长方形纸平分成四等份，然后取其中的3份，就是3/4。

通过以上三个层次的引导，使学生建构起对分数的意义的整体理解，使学生的思维层层递进，从而获得提升和发展。

三、从经验入手，引导系统思维

数学知识具有系统性，前后联系非常紧密，同时也具有差异性，有些问题虽然看起来相似，但实际上比较起来却又大相径庭。这就需要教师合理引导，带领学生深入探究，进行系统化思维，既能够辩证对待知识的正迁移和负迁移，也能够将问题放在一个系统中考虑，而不是孤立地看待问题。

在教学中，教师要让学生学会对知识进行总结和运用，如在教学“轴对称图形”这一知识时，先让学生动手折一折、画一画，得出如下图形（如图1）并思考：观察这些图形，看有几条对称轴，你发现了什么？生：正三角形有三条，正方形有四条，正五边形有五条，正六边形有六条。师：从这个表象中可以发现，是正几边形就有几条对称轴。事实真的如此吗？请举例。生：正八边形有八条对称轴。师：那么圆形呢？这样，学生透过表象获得对抽象知识的思考，从而找到这一表象所蕴含的规律，快速有效地掌握了新知。

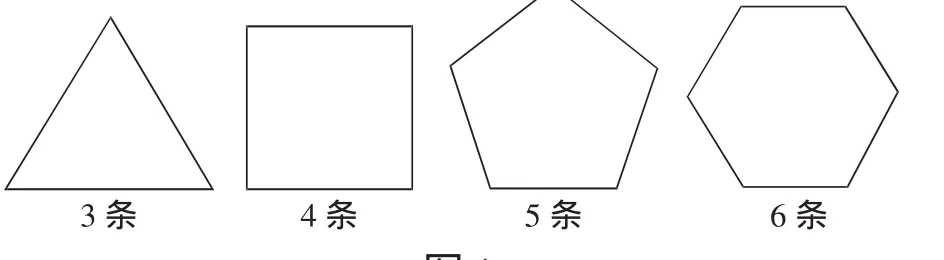
图1

另一方面，教师要加强新旧知识的巩固，让学生学会前后连贯、系统运用。如在教学“能被3整除的数”时，我让学生思考：能被2和5整除的数个位有什么特征？能被3整除的呢？我们是怎样研究能被2和5整除的数的特征的呢？学生发现，研究能被2和5整除的数的特征的方法是在百数表里先圈出这些数，然后进行研究的。那么研究能被3整除的数，也可以采用这种方法。

总之，数学教育的根本目的，是要培养学生的数学素养，使学生全面发展，而只有从数学思辨的训练入手，才能有效推进这一教学进程。