数学中探索性问题的类型及其教学策略

谢秀容

（鼎湖中学，广东 肇庆　526070）

近年来，各省市、自治区的中考数学试题出现了大量探索性类型题目，其所占分值大，难度一般较高，学生对解决这类问题常常感到很困惑，其总体得分率较低。探索性问题没有明显的结论，要求学生通过观察、实验、联想、归纳、分析、类比、比较等获得数学猜想，并进一步寻求证据，给出证明或举出反例，从而得到结论。本文中，笔者就探索性问题的类型和解决方法进行一些探讨。

一、探索性问题的类型

（一）寻找规律型问题

寻找规律型探索性题一般是给出几个有一定规律的代数式，让考生根据其特点归纳可能出现的规律，最后得出自己的结论。在教学过程中，教师不要仅关注学生是否找到了规律，更应关注学生是否进行了思考。如果学生一时未能独立发现其中的规律，教师可以鼓励学生开展相互合作交流，进一步进行探索；教师也可以对学生提供一些帮助，让学生充分感受探索事物数量关系、变化规律的过程，努力培养、提高学生的探索和推理能力。

例1 观察下列等式

9－1=8；16－4=12；25－9=16；36－16=20；……

这些等式反映自然数间的某种规律，设n(n≥1)表示自然数，用关于n的等式表示这个规律为__________。

探索：教师可先向学生提示，自然数n与公式的序数是紧密联系的，存在一定规律，找出这个规律是解决这类题型的关键。用n表示第一个式中的自然数就是1，以此类推，然后探索考究每个等式中的对应项之间与n存在何种关系式。综观以上4个等式存在的规律，上面4个等式中的第一项分别等于(n+2)2,第2项分别等于n2,而4个等式中的右边各项都是4的倍数，8=4×2，12=4×3，16=4×4，20=4×5，由此可知等式右边存在规律为4(n+1),所以用n的等式可将这个规律表示如下：(n+2)2-n2=4(n+1)。

（二）存在型问题

存在型探索性问题一般是给出足够的题设或配备相关的图形后，出题者根据已知的题设提出一些结论，要求考生考究、探索是否存在这样的结论。

例2如图1，矩形ABCD在x轴上，BC的长是4，A的坐标是（-1，0），B的坐标是（2，0），求A、C的直线与Y轴交于点E。

（1）求点E的坐标。

（2）在X轴的正半轴上是否存在点P。

图1 示意图

使OP:PB=CB:OE，若存在，请求出点P的坐标；若不存在，请说明理由。

分析：第(1)问易求，知道了点A、B的坐标及BC的长，用待定系数法可求出过点A、C的直线方程，这个方程为y=4x/3+4/3。因为点E在Y轴上，可知它的横坐标为0，所以它的纵坐标为4/3，即点E﹙0，4/3﹚；至于第﹙2﹚问，由题设可知四边形OBCE是直角梯形，CB:OE即是直角梯形的下底比上底，由第﹙1﹚问题设可知CB=4,OE=4/3,OB=2,所以CB:OE=4:4/3,化简这个比例式得CB:OE=3:1。现要在X轴的正半轴上找一点P，使OP:PB=3:1,可知点P是必然存在的。当点P在线段OB上时，由OB=2,OP:PB=3:1,易求出OP=3/2；当点P在点B的右侧时，由OP:PB=3:1,解得OP=3，所以在X轴的正半轴上存在点P﹙3/2，0﹚或P(3，0)，使得OP:PB=CB:OE。

（三）判断型问题

判断型探索性题基本上是由给出的题设条件，要求学生判断一些结论是否正确，并加以推理论证。

例3 如图2，在等腰梯形ABCD中，AB∥CD,AC、BD是对角线，将△ABD沿AB向下翻折到△ABE的位置，试判定四边形AEBC的形状，并证明你的结论。

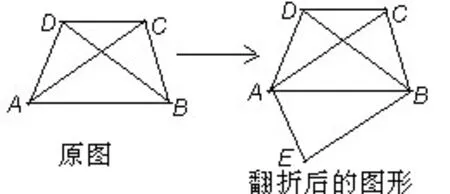
图2 示意图

探索：由本题的题设可知四边形ABCD是等腰梯形，△ABE是由△ABD沿AB翻折所得，要充分应用等腰梯形的性质、对称的性质以及全等三角形等知识。

探索推理过程：

因为四边形ABCD是等腰梯形，所以∠DAB=∠ABC,AD=BC,

又因为△ABE是由△ABD沿AB翻折所得，

所以△ABE≅△ABD，AD=AE，∠DAB=∠EAB，

所以∠EAB=∠ABC,从而得AE∥BC,AE=BC。

综上探索可知四边形AEBC是平行四边形。

（四）条件探索型问题

条件探索型问题是仅给出给定的结论，要求探求此结论成立应具备的充分条件。

例4如图3，己知AB、CD相交于点O,AB=CD,试添加一个条件使得△AOD≅△COB,你添加的条件是_________（只需写一个）。

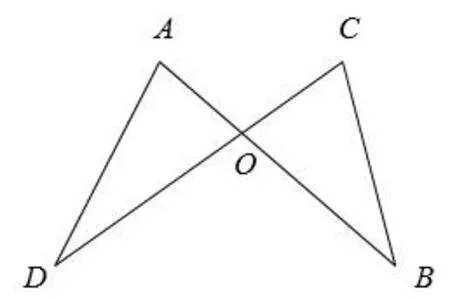
图3 示意图

分析：本题要得到结论△AOD≅△COB。己知∠AOD=∠COB，结合己知条件考虑用“边角边”证明全等。如AO=CO和DO=BO中有一个结论成立，则另一个结论也成立。

答案：添加AO=CO或DO=BO。

（五）结论探索型问题

结论探索型问题是指题中没有给出明确结论的问题。

例5如图4，AB=CD,BC=CD,AC和BD相交于E。由这些条件可以得出若干结论，请你写出其中3个正确结论。（不要再添加字母和辅助线，不要求证明）结论1：________；结论2：_______；结论3：______。

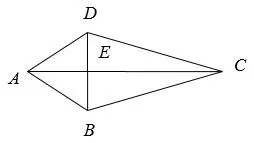
图4 示意图

分析：由AB=AD，可得∠ABE=∠ADE;由BC=CD可得∠CDE=∠CBE；由AB=AD,AC=AC，可得△ADC≅△ABC,从而∠ADC=∠ABC；由等腰三角形三线合一性质可知AC⊥BD,BE=DE

解 结论 1：AC⊥BD；结论 2：BE=DE；结论 3：∠ADC= ∠ABC。

点评：解决这类问题的一般思路是，从分析题意人手，充分捕捉题设信息，通过由因导果、顺向推理或联想类比猜想等，获得所求结论。一般情况下，结论是开放的。

二、探索性问题的教学策略

初中学生往往觉得探索题神秘、抽象，新的课程标准加强了对学生探索、推理能力的培养，因而教师研究、总结培养学生探索能力问题是很有必要的。

（一）积极激发学生的探索兴趣

兴趣可激发一定的情感，唤起某种动机，培养人的意志，使学生真正成为学习的主人。在设计导入时，教师可根据学生的年龄特征和学习心理状态进行精心策划，以激发学生的求知欲望和探究的内在动机。

（二）启发探索思维

在教学过程中，教师要注重传授给学生一些思维方法，如辨证法、类比思考法、对立思考法、转换思考法，等等。鼓励学生发展创新思维，自由思考、标新立异，指导学生运用形式逻辑与辨证逻辑进行推理探索。

（三）培养探索能力

能力的发展绝不同于知识与技能的获得，探索能力的形成是一个缓慢的过程，有其自身的特点和规律，因而教学活动必须给学生提供探索交流的空间，组织、引导学生经历观察、实验、猜想、证明等数学活动过程，这样就能拓宽和发展学生的推理、探索能力空间，有效地发展学生的探索能力。

（四）培养意志品质

掌握解答探索性类型题并非容易之事，有的学生往往因缺乏意志和毅力半途而废、无功而返，有的学生则事半功倍。在教学过程中，教师要着力培养、锻炼学生的意志与毅力,良好的意志品质对其智能的发展具有强化和推动作用。

总之，教师在教学过程中要认真贯彻新课程标准的要求，大力培养学生的推理、探索能力。通过让学生经历和探索事物数量关系、变化规律的过程，达到提高学生数学思维活动水平的目的，从而使学生更好地领悟探索的本质。