基于Schwab-Knopoff算法的优化改进

王国富，许崇彩，张法全

(桂林电子科技大学信息与通信学院，广西桂林541004)

0 引言

由于瞬态瑞雷波勘探具有能量强、衰减小、轻便、快捷、高效、分辨率高、不受各地层速度关系影响等优点，广泛应用在土层分层、地震勘探、浅层煤田勘探和地下煤层勘探[1－4]。研究表明:瑞雷面波在非均匀介质中传播时产生频散现象，即其传播相速度VR是面波w的函数，F(w，VR)为面波的频散函数，曲线w－F是面波的频散函数曲线，而瑞雷波频散曲线与地下介质结构密切相关，所以如何提取准确可靠的频散曲线是瑞雷波勘探技术的关键问题之一[5－7]。

前人对瑞雷面波曲线的提取已作过一些研究。较好的瑞雷波频散函数理论计算算法主要有Thomoson-Haskell算法、Schwab-Knopoff算法、δ矩阵算法和RT矩阵法。Thomoson-Haskell方法在Thomson研究基础上，通过相邻两界面的传递矩阵公式以及自由表面边界条件和无穷远处的辐射条件推导出了层状介质中平面瑞雷波的方程，但是此方法应用于高频容易出现数值溢出及精度丢失问题[8];Schwab和Knopoff在Knopoff快速计算的基础上进一步研究和改进，提出“归一化”、“细分层法”，降低了有效数字的损失，计算溢出得到了改善，但是仍没有完全消除[9－10]。文献[11]采用的柱坐标系法降低了数值的不稳定，但并没有完全消除;δ矩阵算法吸收了Schwab的变换程序思想，具有快速稳定的特点[12]，但是频散曲线粗糙，尤其在高频处曲线更加弯曲;RT矩阵法采用了反射和透射子矩阵技术，巧妙地避开了数值的不稳定性，但是这种方法要求所有的计算机均使用复数计算形式，故计算量大[13]。

针对Schwab-Knopoff容易造成数值溢出和丢失的缺陷，笔者在Schwab-Knopoff快速算法的基础上提出了算法的简化方法，并编程予以实现。

1 Schwab-Knopoff快速算法原理

Schwab-Knopoff快速算法的主要计算思路是根据上一层地质参数不断由层参数递推出新的矩阵元素，即由m层的矩阵元素推算出m+1层的矩阵元素，一直计算到n－1层界面为止。根据Schwab-Knopoff快速算法的推导，n层半无限空间介质的瑞雷波频散函数为4n－2的行列式，频散函数F(w，VR)最终形式为[14]:

2 Schwab-Knopoff算法改进

Schwab-Knopoff快速算法虽然应用比较广泛，但是在高频率计算频散曲线时很容易出现高频数值溢出的问题，对于实际的勘探有一定的限制，无法很好地解释实际勘探中的问题，使反演受到了限制。仔细分析该算法原理公式时发现，有些计算因子会对数值产生很大的影响，频率数值的一点变化就能导致频散函数数值产生很大的变化(采用的层状地质模型、地质参数如表1所示)。

表1 层状介质各参数值Table 1 Layered media parameter values

当m为奇数时，公式的展开式为[14]

由以上公式推导可看出，矩阵函数AX为同一数量级的矩阵，矩阵函数BX除了第1行外，其他4行为kεiξj的形式。如果VR小于VSm，那么该层对应的矩阵含有cos(Pm)和cos(Qm)两项，由于Pm=kγαmdm、Qm=kγβmdm(k是波数;d是厚度;γ为表达式)，那么为频率的指数函数，当频率比较高时，cos(Pm)、cos(Qm)为一很大的数量级，很可能超过计算机的最大数限制，出现无穷大，使计算不能顺利进行，即出现高频数值的溢出问题。本文对于层状介质模型(介质参数见表1)计算了传递矩阵中用到的参数ξi(i=7，8，…，15)(公式迭代中运用到的元素为ξ7，ξ8，…，ξ15)、εi(i=1，2，…，15)值的最大和最小值，如表2所示。

表2 ξi、εi最大值和最小值Table 2 Maximum and minimum of ξiand εi

可以看出:当f=2 000 Hz、VR=100 m/s(不是高频阶段)，ξi(i=1，2，…，6)为无穷大，说明已经超出了计算机的数值上限，在搜根时可能会造成有效根的丢失;当f=5 000 Hz、VR=2 200 m/s时(情况与f=8 000 Hz，VR=2 100 m/s时相差不大)，ξi最小数量级为1013，而εi与ξi相差1012，相对于ξi来说，εi与0可以完全忽略不计;当f=5 000Hz，VR=3 000 m/s时，ξimin与εi在同一数量级，ξimax相对大一些，但不会造成很大影响。总之可以看出，当VR＜VS(i)时，在某段频率内εi与ξi相差比较大，完全可以省略εi，使整体的数值减小，提高有效数字的长度，避免或者减小有效数字的丢失，提高精度，从而得到有效可靠的频散函数图形。当高频时也能起到相同的提高精度的作用。所以可以采用如下的化简方法:

因为ξm=kcos(Pm)cos(Qm)(m=7，8，…，15)，在高频和低频阶段情况下，当VR小于VSm时，那么该层对应的矩阵含有cos(Pm)和cos(Qm)，为一大数量级。当cos(Pm)为大数量级时(设大于1040)，sin(Pm)=icos(Pm)，而矩阵的每个元素都可以表示为k1cos(Pm)cos(Qm)+k0，因为此时的cos(Pm)为非常大的数据，且k0相对于k1cos(Pm)cos(Qm)项完全可以忽略不计(由表2可见)，故在此层的传递矩阵中的元素可以化为cos(Pm)=1，sin(Pm)=i，k0=0，则完全不影响频散函数的求根;同样，当cos(Qm)为大数量级时，sin(Qm)必为大数量级，且有sin(Qm)=icos(Qm)，而矩阵的每个元素都可以表示为k1cos(Pm)cos(Qm)+k0，因为此时的cos(Qm)为非常大的数据，则cos(Pm)必为很大的数据(横波波速VSm小于纵波波速VPm)且k0相对于k1cos(Pm)cos(Qm)项完全可以忽略不计，故在此层的传递矩阵中的元素可以化为cos(Pm)cos(Qm)=1，sin(Qm)sin(Pm)=－1，k0=0，则完全不影响频散函数的求根，而且能够提高有效数字的精度。

根据简化算法，上述公式的元素简化如下:

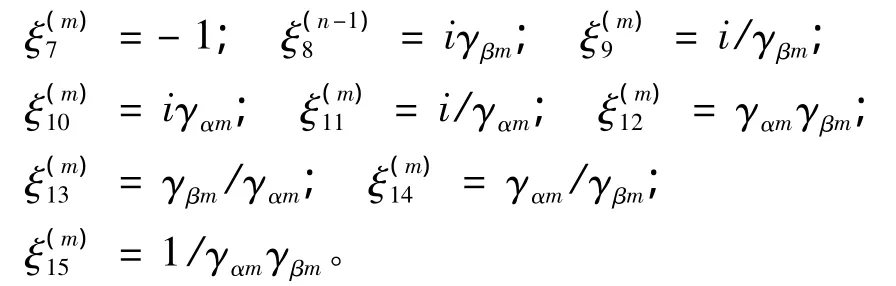
可见元素数值大为简化，能够减少数据的计算时间，并且εi与ξi能够在一个数量级内(表3)，有效地减少有效数字的损失和数值的溢出。

表3 简化后ξi、εi最大值和最小值Table 3 Maximum and minimum of simplified ξiand εi

3 改进算法的结果分析

实验采用的层状介质模型如表1所示。实验模拟时，当计算数值大于1040时调用简化算法，否则就用原算法。当频散函数绝对值小于10就画出该点，频散函数绝对误差如表4所示，0～5 000 Hz频率范围内的频散函数分布如图1、2所示。

从表4可以看出，原Schwab-Knopoff算法的函数绝对值偏大，有的超出范围;在频散函数曲线上(图1)，超过3 500 Hz以后无法准确的分辨出正常的频散曲线;而修改后的算法和δ矩阵法能够得到准确而清晰的频散曲线(图2、3)，为反演及其地质层解释打下良好基础。

表4 频散函数绝对误差Table 4 Dispersion function of absolute error

图1 原Schwab-Knopoff算法频散图Fig.1 Dispersion diagram of original Schwab-Knopoff

图2 改进后的Schwab-Knopoff频散图Fig.2 Dispersion diagram of improved Schwab-Knopoff

从原算法频散图(图1)还可以看出:该算法在低频(＜1 000 Hz)时因为有效数字丢失或者数值溢出，导致频散函数失真，不能准确提供信息;在中频(1 000 Hz＜f＜3 500 Hz)由于数值在计算机数值限制范围内，εi与ξi相差不大，能够提供准确的频散图形;但是高频(＞3 500 Hz)阶段由于εi与ξi相差比较大，出现严重的数值精度丢失问题。这是因为计算中存在一些大数量级的量，在理论上能够相减消去，但是数值上的误差积累不能消去，即使有原算法的归一化，也会导致数值溢出不能得到正确的结果，使计算不能顺利进行，即出现了数值的溢出。这将导致频散函数严重失真，频率越大，高阶频散图失真越厉害，无法提供可靠准确的频散图，导致后续工作无法正常进行。修改后的Schwab-Knopoff快速算法的频散图如图2所示:该算法在低频(＜1 000 Hz)时能够很好地处理计算机数值溢出和有效数字，得到很好的频散图形;在中频(1 000 Hz＜f＜3 500 Hz)和原算法的处理结果一样;在高频(＞3 500 Hz时)阶段调用的简化算法，能够很好地处理高频部分数值的溢出，从而确保了数值的精度，实现了正演算法的正确运行，为反演打下了很好的基础。图3为δ矩阵法的频散图，与改进后的算法频散图一致，验证了算法的正确性，为地球物理勘探提供了准确的频散曲线和理论研究。

4 结论

图3 δ矩阵法的频散图Fig.3 Dispersion diagram of δ matrix method

在仔细研究原Schwab-Knopoff快速算法的基础上，提出了该快速算法的简化方案。实验结果表明:该简化算法简单易行、数据简单，不仅能够较快速的计算实验的频散图，还可解决低频和高频阶段的上下限溢出和有效数字丢失的问题，使实验频散的有效频率达到5 000 Hz以上，能够提供准确的频散函数曲线，尤其是清晰准确的高阶频散图，为反演的复杂性提供准确的理论参考，并为瑞雷波的实际勘探提供强有力的理论基础和依据，满足实际的勘探需要，具有很大的发展潜力。

[1]Xia J H，Miller R D，Xu Y X，et al.High-frequency Rayleigh-wave method[J].Journal of Earth Science，2009，20(3):563－579.

[2]Lu J Q，Li S Y，Li W，et al.A hybrid inversion method of damped least squares with simulated annealing used for Rayleigh wave dispersion curve inversion[J].Earthquake Engineering and Engineering Vibration，2014，13(1):13－21.

[3]童立元，陈征宙，方磊，等.瞬态瑞雷波法在工程检测中的应用[J].桂林工学院学报，1999，19(4):334－338.

[4]周文宗，熊章强，张大洲.基于软弱夹层模型的瑞雷面波各模式相速度敏感性分析[J].桂林理工大学学报，2013，33(4):629－633.

[5]Xia J H，Xu Y X，Miller R D，et al.New developments in analysis of high-frequency Rayleigh waves[C]//Goephysical Solutions for Environment and Engineering:Proceedings of the 2nd International Conference on Environmental and Engineering Geophysics，2006，1:10－18.

[6]刘雪峰.层状介质中瑞利面波多模式性质及其在正反演中的应用[D].哈尔滨:哈尔滨工业大学，2011.

[7]肖柏勋，李长征.瑞雷面波勘探技术研究述评[J].工程地球物理学报，2004，1(1):38－47.

[8]邵广周.多阶模式瑞利波频散特征与反演研究[D].西安:长安大学，2009.

[9]邓乐翔.瑞雷波场正演模拟及频散曲线的提取[D].西安:长安大学，2010.

[10]焦健.基于空间自相关法的微动勘探技术的研究[D].长春:吉林大学，2012.

[11]张碧星.半无界分层介质表面任意面源激发的弹性波场[J].声学学报，2007，32(3):193－204.

[12]杨威.瑞雷波在岩溶勘查中的应用研究[D].长沙:中南大学，2012.

[13]张凯.粘弹性介质瑞雷波模拟及其频散曲线反演[D].武汉:中国地质大学，2011.

[14]曾校丰，崔伟群，许维进，等.瑞雷波频散函数的快速算法[J].地球物理学报，2002，45(S1):261－267.