履带对履带车辆车体振动影响的分析
孟 磊, 李晓雷, 邱 实, 奚浩晨
(北京理工大学 机械与车辆学院,北京 100081)
履带对履带车辆车体振动影响的分析
孟 磊, 李晓雷, 邱 实, 奚浩晨
(北京理工大学 机械与车辆学院,北京 100081)
基于LMS Virtual.Lab Motion建立了以行动系统为主的车辆—履带动力学模型和车辆—试验台架动力学模型(不含履带).利用仿真结果对比了两种模型在不同车速、不同路况下车体质心垂向振动加速度功率谱密度曲线的变化情况.从而分析出履带对车体振动的影响,同时也为履带车辆室内道路模拟试验的准确度提供了一定的参考.
履带车辆;车体振动;动力学模型;LMS Virtual.Lab Motion
在验证履带车辆整车性能的过程中,由于实际道路试验不仅会受到场地、时间等因素的限制,实时测试也比较困难,因此道路模拟台架试验被广泛应用. 履带车辆道路模拟台架试验不受场地、时间的限制,可以在一定精度范围内模拟实车行驶中的多种工况,同时便于测试装置的安装布置,具有十分重要的应用价值.
在实际室内道路模拟试验过程中,由于关注点一般在车身和悬挂系统上,履带车往往不挂履带,这样履带对车体振动的影响就经常被忽略了,而即使挂有履带,其工作方式也与实际行车有很大区别. 明确在室内道路模拟试验中履带对车体振动的影响,可以使试验更加真实可靠.文献[1]从理论方面较详细的分析了履带对车体振动的影响,但不够直观. 随着ADMAS、LMS Virtual.lab等多体动力学软件的成熟,可以通过多体仿真,直观的分析这一问题. 基于LMS Virtual.lab Motion分别建立了实际道路行驶模型及台架试验模型,通过仿真结果对比,分析了履带对车体振动的影响,对于实际试验来说也具有一定的参考价值.
1 多体系统动力学方程的建立[2]
LMS将多刚体系统动力学传统算法与递归算法相结合,基于DADS高效稳定的求解器,建立虚拟机械系统动力学方程[3].
1.1 广义坐标的选择
三维空间中的每个刚体都有6个自由度(3个平移自由度和3个转动自由度). LMS Virtual.Lab Motion中,刚体平动采用第i个刚体的质心笛卡尔坐标来进行描述. 应用欧拉四元数[e0,e1,e2,e3]来对刚体的空间姿态进行描述. 这有效的解决了采用欧拉角时,可能带来的矩阵奇异问题. 即每个刚体用7个广义坐标描述qi=[x,y,z,e0,e1,e2,e3],q=[q1T,q2T,…… ,qT]T其中的欧拉四元数中的4个参数的平方和等于“1”. 因为采用了不独立的广义坐标,系统中的动力学方程是数量最大且高度稀疏的微分代数方程,因此,适于用求解稀疏矩阵的方法来进行高效的求解.
1.2 多刚体系统动力学方程的建立
采用拉格朗日乘子法,由此多刚体系统的动力学方程为
(1)
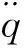
系统约束方程为
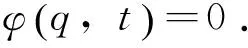
(2)
求约束方程对广义坐标偏微分,可得到约束方程雅可比矩阵φq.
(3)
速度方程为
(4)
加速度方程为
(5)
由加速度方程得到拉格朗日乘子γ的表达式为
(6)
通过介绍LMS Vittual.lab Motion中应用到的多体动力学理论,对其动力学求解原理进行阐述,便于了解其求解器在计算中产生误差的原因及误差的数量级.
2 动力学模型建立
2.1 车辆—履带模型
根据履带车辆各部件的实际尺寸,在LMS Virtual.lab Motion的环境中建立包括车身和行动系统的三维几何模型. 对其添加约束、驱动力和接触力建立动力学模型,如图1所示. 为了计算方便,通过在车身中心和地面之间添加平面副(Plnanr Joint)的方法,限制车辆的侧倾运动和横向平移,从而将整车模型改为半车模型. 同时将车身质量和各方向上的转动惯量数值减半,并将质心平移至新的相应位置.

图1 履带车辆动力学模型及路面模型
履带与地面、负重轮、拖带轮、诱导轮、主动轮之间的接触力用force/contact单元中的球对拉伸面接触(sphere to extrude)和球对旋转面接触(sphere to revolve)来模拟,所用的接触理论为赫兹接触. 该模型中的悬挂采用扭杆弹簧式,可以通过调整扭簧的预扭角来保证平衡肘的静倾角,减振器采用叶片式. 调整履带预张紧力,使其在车重的8%~10%之间[4].
该模型中的硬路面利用真实的路面高程信息,在CATIA中生成路面曲线,再导入到LMS Vitllal.Lab Motion中生成可以定义接触的加厚曲面.
2.2 车辆—试验台架模型(不含履带)
如图2所示,履带车仍为半车模型,将路面替换为6通道的激振台. 激振台与地面之间通过圆柱副(cylindrical joint)约束,保证其垂直方向的直线运动. 激振台的驱动用constraints/position drivers单元中的two-body position driver来定义,定义好后,6个激振台将分别按照各自输入的时间—路面高程序列动作,模拟车辆在真实路面上的行驶情况. 负重轮与激振台的接触用球对旋转面接触(sphere to revolve)来定义.
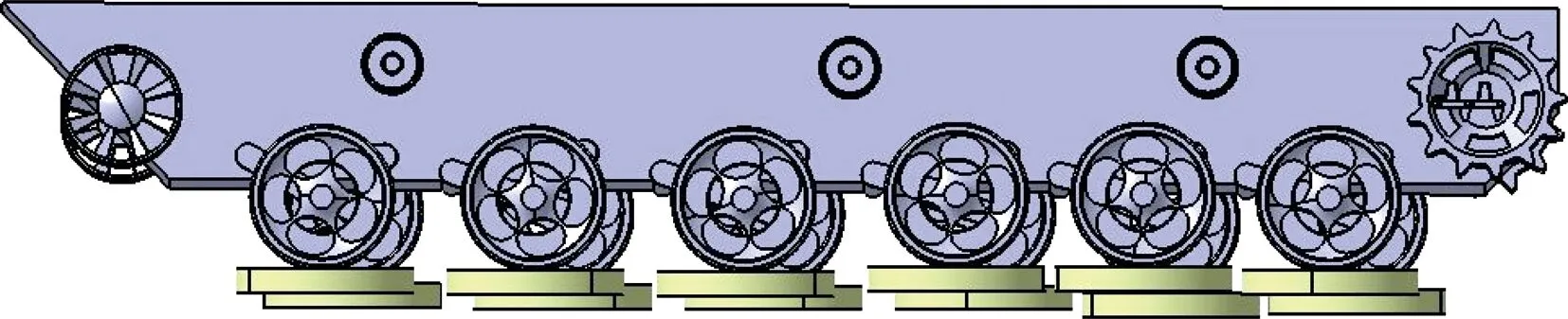
图2 车辆—试验台架模型
3 履带对车体振动影响分析[1]
3.1 对路面不平度的影响
履带对路面不平度有两个方面的影响. 一方面它滤掉了路面不平中比履带板节距空间频率更高的成分,使履带板节距的空间频率nT成为路面不平度的上限频率;另一方面每两块履带板连接处的缝隙,又在路面不平度中增加了与履带板节距相应的周期性激励. 若履带板的节距为tT,则由履带板构成的空间频率为nT=1/tT.当车速为u时,路面不平度的时间频率上限为fu=nTu. 目前履带车辆的nT= (120~190)mm,当车速u=(10~80) km/h时,路面不平度的时间频率上限fu=(14.62~185.2) Hz.
3.2 履带预张紧力对悬挂的影响
履带有预张紧力,当车首的负重轮通过较高的不平物后,与之相连的悬挂弹性元件由于受到履带的限制不能自由伸张,伸长量达不到负重轮的静行程,从而降低了该负重轮悬挂对后继障碍物的缓冲能力,有加大后继俯仰振动的可能.
3.3 履带引起的振动“牵连”
车辆振动,特别是俯仰角振动,将使前、后支履带一端伸张,一端缩短,非驱动区段的履带长度变化,可借助诱导轮的转动从上支履带得到补偿,使该区段履带张紧力不致发生较大变化. 驱动区段的履带由于与主动轮啮合,其长度变化必然会引起该区段履带牵引力变化,迫使车辆产生“牵连”的纵向运动,原先等速行驶的车辆,行驶速度将忽快忽慢,使车体的部分振动能量消耗在行驶阻力上,有助于车体振动的减振.
由上述分析可知,履带预张紧力有增大车体振动的趋势,而履带引起的振动“牵连”有助于减小车体的振动,其综合效果对车体振动的影响可能增大,也可能减小.
4 仿真及结果分析
4.1 仿真试验设计
利用车身质心垂向振动加速度来分析履带对车体振动的影响,考虑了路面等级和车速这两个外在因素. 仿真工况如下表1所示.
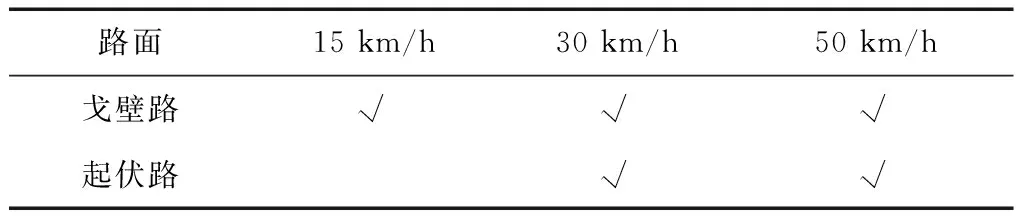
表1 仿真工况
表中,戈壁路属于D级路面,起伏土路属于D级与E级混合路面. 15 km/h车速的设定,主要出于如下考虑:模型中履带板节距tT=137mm,当车速u=15 km/h时,则由履带板节距所产生的周期性激励的时间频率fu= 30.4 Hz,与负重轮垂直线振动固有频率30 Hz接近,此时履带板连接处的不平,会对负重轮的负荷有较大影响.
仿真过程的采样频率为200 Hz,采样时间为32 s(已去除落车及车身恢复平稳所需时间). 履带预张紧力设为车重的10%(车重约30 000 kg).
4.2 仿真结果
根据实际经验履带车辆车体俯仰角振动固有频率约为1.1 Hz,车体垂直线振动固有频率约为1.5 Hz[1].
1) 路面和车速的影响
图3~7分别为表1中所述5种工况下,两种模型车身质心垂直振动加速度功率谱密度曲线.由于受总采样点数较少的限制,部分工况下的车身垂直线振动固有频率或俯仰角振动固有频率会不明显.
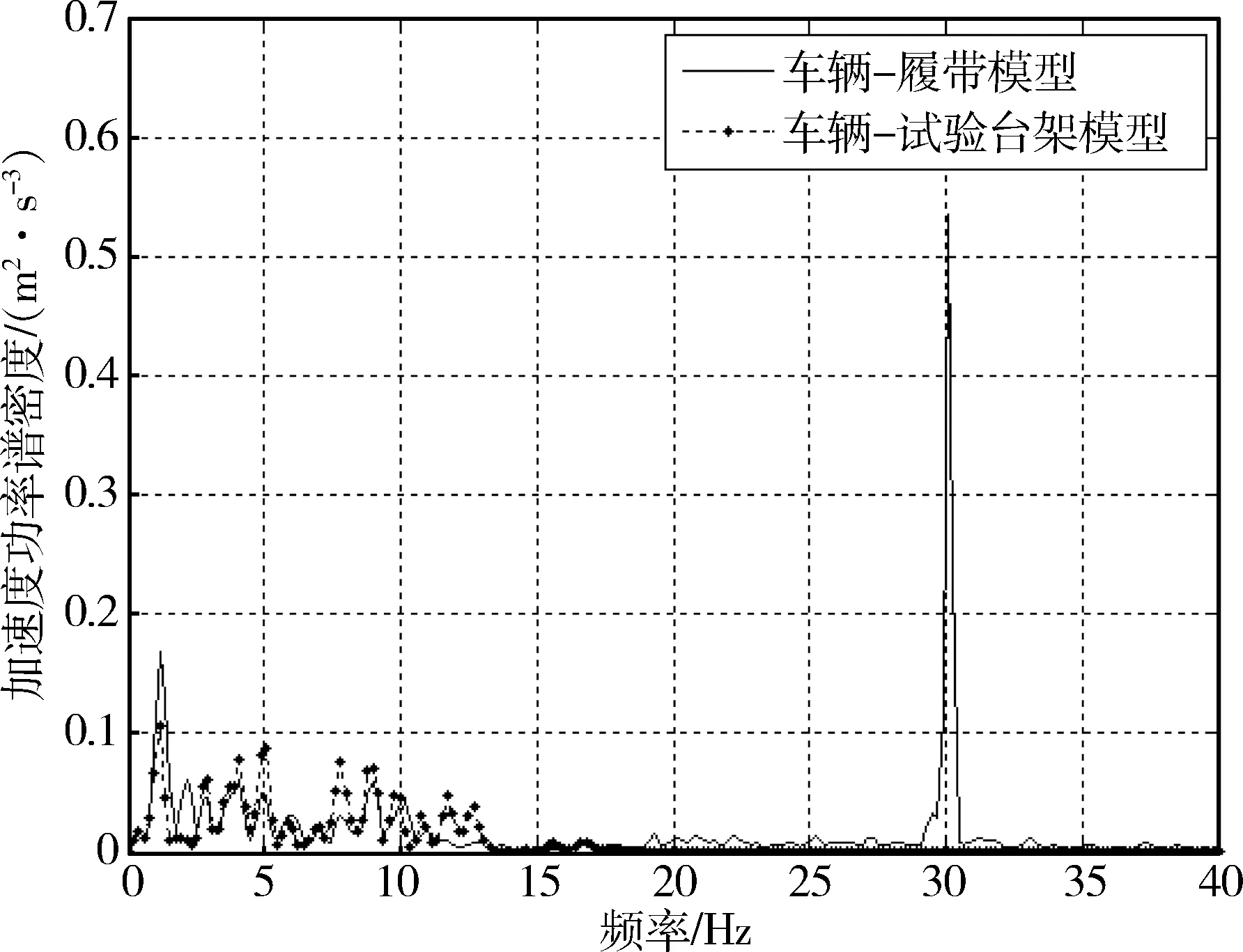
图3 戈壁路15 km/h
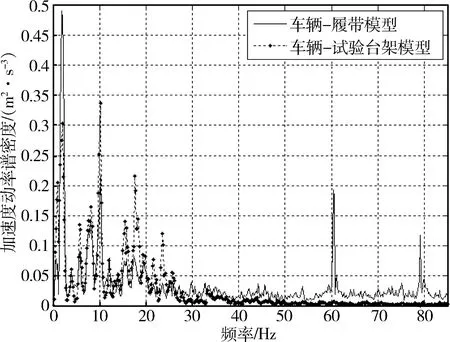
图4 戈壁路30 km/h
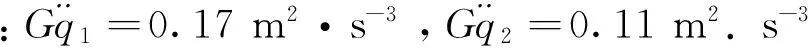
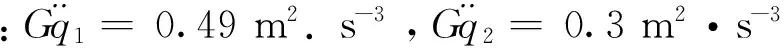
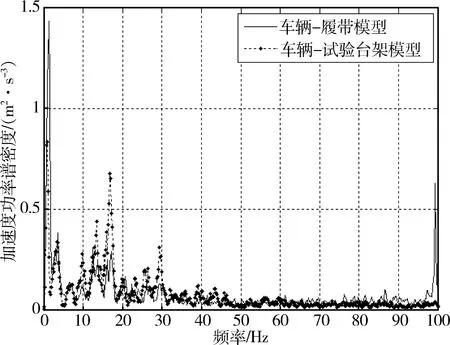
图5 戈壁路50 km/h
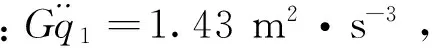
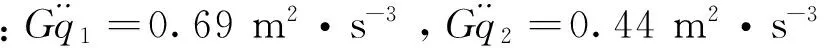
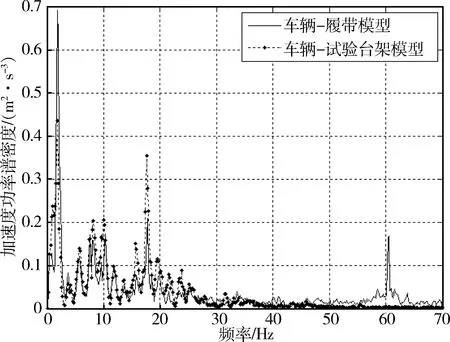
图6 起伏土路30 km/h
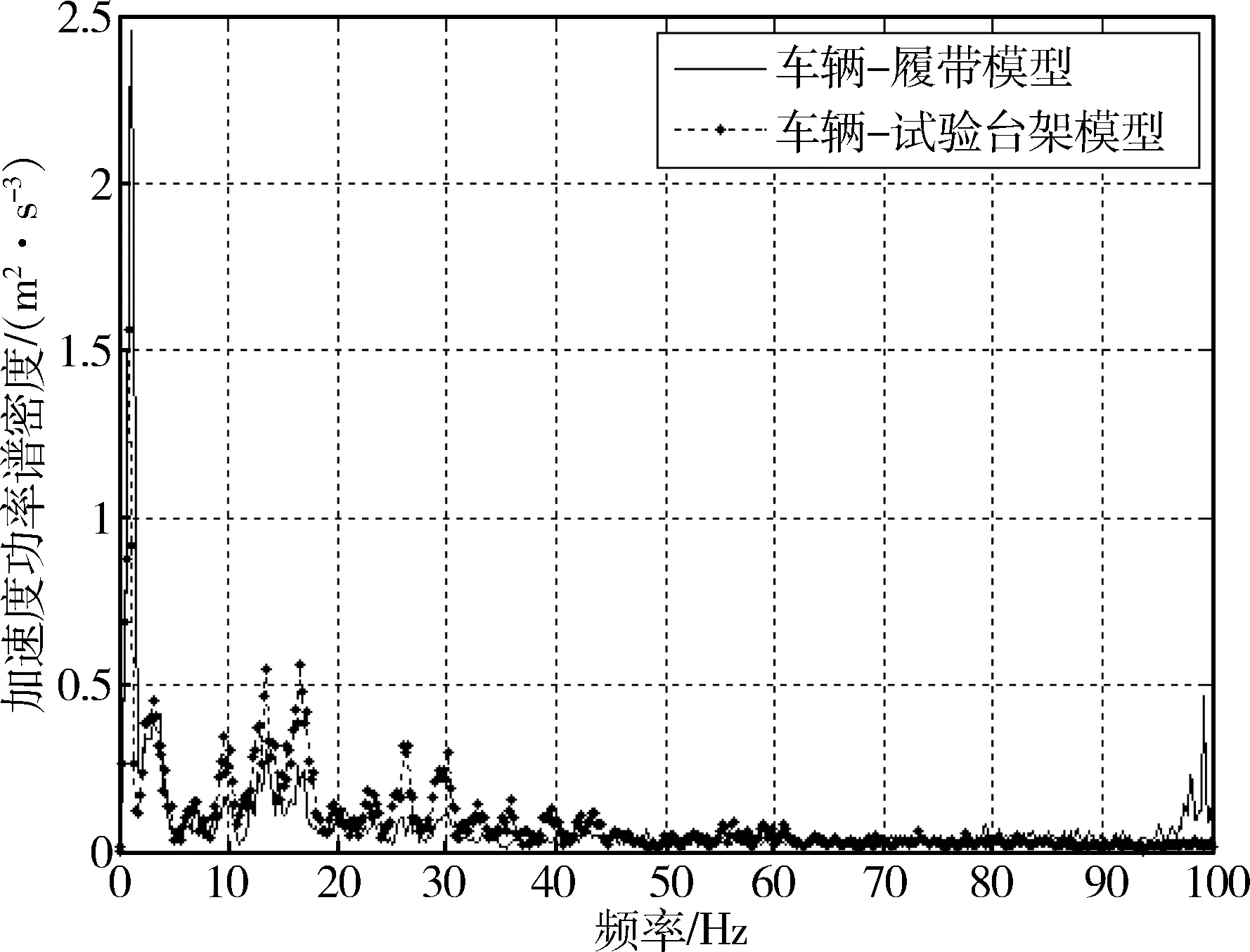
图7 起伏土路50 km/h
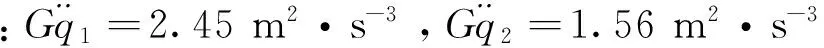
2)履带预张紧力的影响
图8为戈壁路30 km/h,有履带模型在履带预张紧力分别为10%和15%时,车身质心垂直振动加速度功率谱密度曲线. 图9为戈壁路30 km/h,履带预张紧力为15%的有履带模型与试验台架模型车身质心垂直振动加速度功率谱密度曲线.

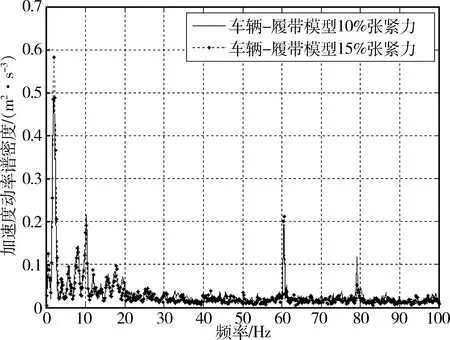
图8 戈壁路30 km/h
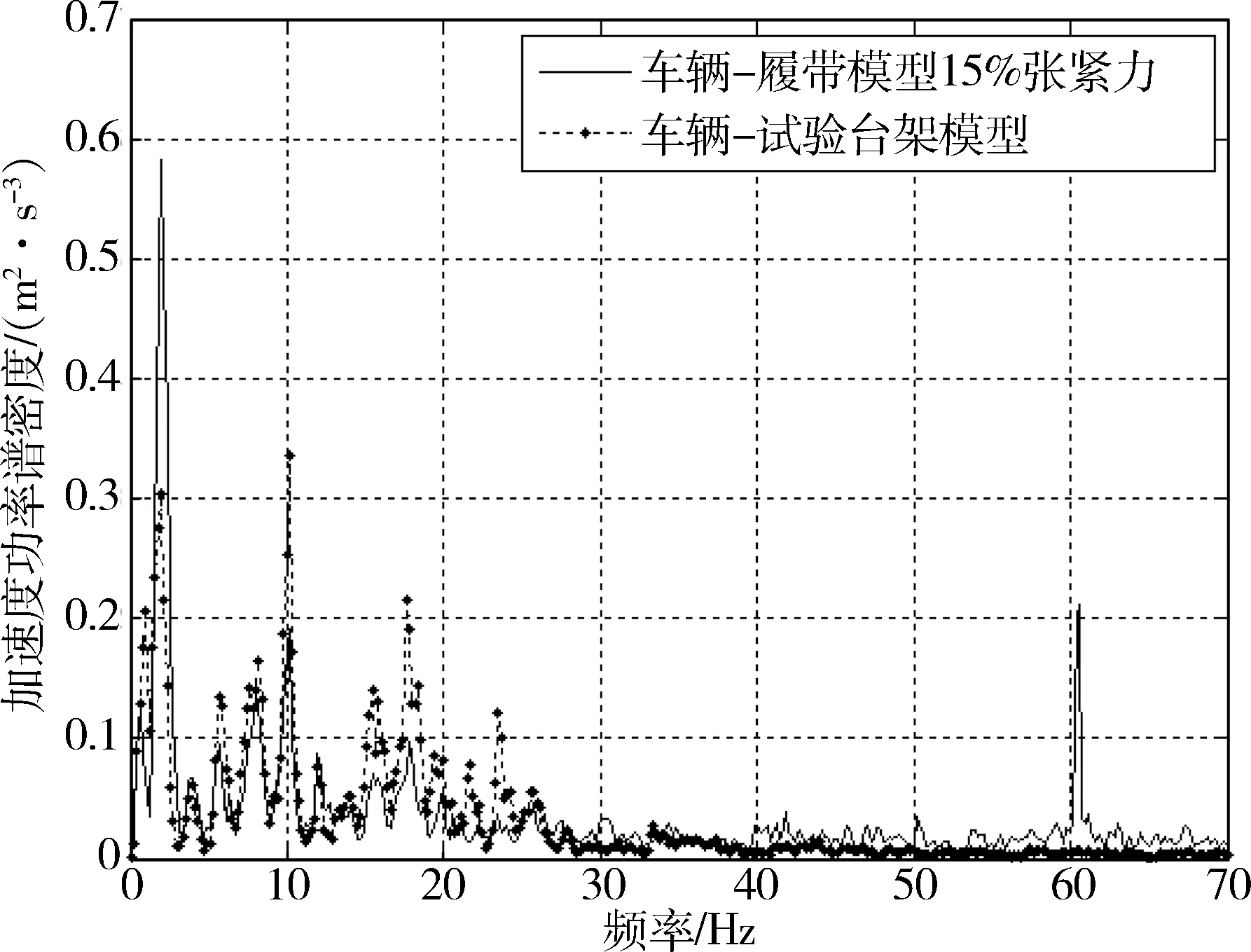
图9 戈壁路30 km/h
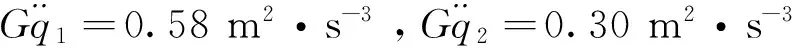
4.3 结果分析
1) 由图3~7中曲线可以看出在0~2 Hz的频段内均有明显的峰值,此频段内包含有车身垂直线振动固有频率和俯仰角振动固有频率. 由于总采样点数较少部分工况中的固有频率不明显,但也可以通过均值大致得到:车辆—履带模型的垂直振动固有频率为1.76 Hz,俯仰角振动固有频率约为1.02 Hz;车辆—试验台架模型的垂直振动固有频率为1.85 Hz,俯仰角振动固有频率为0.98 Hz. 与实际履带车辆垂直振动固有频率1.5 Hz,俯仰角振动固有频率1.1 Hz比较接近,从一定程度上可以说明文中所使用的模型是合理的,仿真结果具有一定的参考价值.
2) 从图3~7可以看出,由履带板节距引起的周期性激励对车体振动的影响较为明显,特别是在其激励频率约为30 Hz时,会引起负重轮的共振,加剧车身的振动. 但由于其频率较高,对驾驶员舒适性的影响不大.
3) 从图8可以看出,履带预张紧力的增大有增加车体振动的趋势,但由于受到履带“牵连”的影响,部分振动能量被消耗,综合增大效果不明显.
4) 计算图3~7和图9这6种工况下对应的加速度均方根值,主要考虑车身振动对驾驶员的影响,故截取频率为0~20 Hz[5]. 表2为0~20 Hz范围内两种模型车身垂向振动加速度均方根值,数值单位为(m/s2). 1~6工况分别为:戈壁路15 km/h、戈壁路30 km/h、戈壁路50 km/h、起伏土路30 km/h、起伏土路50 km/h、戈壁路30 km/h张紧力15%. 模型1为车辆—履带模型,模型2为车辆—试验台架模型. 从表中可以看出,在这6种工况下有履带模型的车身垂向加速度均方根值均小于试验台架模型,从综合影响来看履带起到了减小车体振动的作用.
在已验证模型正确的前提下,车辆—履带模型可以看作实际道路车辆,车辆—试验台架模型可以看作实际道路模拟试验车辆. 因此,由表2数据可以看出室内道路模拟试验所得的0~20 Hz范围内车体垂向振动加速度均方根值与实际道路车辆所得结果相比,误差在8%以内.
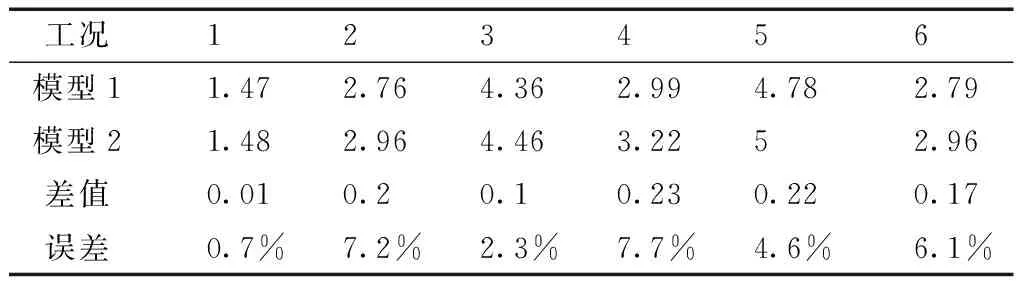
表2 0~20 Hz范围内加速度均方根值比较
5 结 论
1)对于履带车辆室内道路模拟实验来说,其所得车体振动结果比实际情况略大.
2) 于履带车辆室内道路模拟实验来说,履带车辆在车速为15 km/h~50 km/h,路面等级为D级和E级,在研究车体振动时,所得结果与实际道路行驶结果相比,误差在8%以内.
[1] 丁法乾.履带式装甲车辆悬挂系统动力学[M].北京:国防工业出版社,2004.
[2] 万晓峰,刘岚.LMS Virtual.Lab Motion入门与提高[M].陕西:西北工业大学出版社,2010.
[3] 高晓东.基于LMS的履带车辆多体动力学建模与仿真[C]//LMS公司.LMS2013年用户论文集.北京:LMS公司,2014.
[4] 肖永开,李晓雷.高速履带车辆履带预张紧力对平顺性的影响[J].计算机仿真,2006(7):253-259.
[5] 余志生.汽车理论[M].北京:机械工业出版社,2009.
Influence Analysis of Tracks on Body Vibration for a Tracked Vehicle
MENG Lei , LI Xiao-lei, QIU Shi, XI Hao-chen
(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)
A vehicle-track (including suspensions) dynamics model and a vehicle-testbench (excluding tracks) dynamics model are established in LMS Virtual.Lab Motion. The power spectral density (PSD) curves of its body vertical acceleration in two models are compared under the conditions of the vehicle both in different speeds and on different roads. The effects of the tracks on the body vibration are analyzed. The results provide a certain reference for the accuracy of the indoor road simulation test of the tracked vehicle.
tracked-vehicle;body vibration;dynamics model;lMS Virtual.Lab Motion
1009-4687(2015)04-0001-05
2015-9-3
孟 磊(1988-),男,硕士.
TJ811
A

