某矿用汽车动力性换挡规律设计及优化

张晓聪， 孙 良， 王伟达， 闫清东

(北京理工大学 车辆传动国家重点实验室，北京100081)

某矿用汽车动力性换挡规律设计及优化

张晓聪， 孙 良， 王伟达， 闫清东

(北京理工大学 车辆传动国家重点实验室，北京100081)

针对矿用汽车设计了动力性换挡规律，利用MATLAB/Simdriveline建立整车动力学模型进行仿真，验证了车辆的动力性能. 为了得到针对所建仿真模型最优的换挡点，提出以加速时间为目标，用ISIGHT调用MATLAB对换挡点进行优化，并与设计换挡规律进行动力性对比. 结果表明，优化得到的换挡规律加速时间减少、动力性更好.该方法可以方便、快速、有效地修正优化变量，对换挡规律设计和改进以及其他动力学仿真中参数的优化有实际意义.

矿用汽车；动力性换挡规律；优化；建模与仿真

作为主要工作在矿山上的重型车辆，矿用汽车是一种特殊的非公路车辆，行驶路况复杂、工作环境恶劣、负载变化范围很大、动力性和经济性较差，换挡规律的制定对矿用汽车尤为重要.

按理论设计的换挡规律，虽在一定程度上可使汽车获得最佳的性能指标，但并没有考虑到汽车行驶环境和驾驶员的操纵习惯以及控制策略等对整个换挡过程的影响.因而，可以采用优化软件对其优化得到实际更优解. 国内针对矿用汽车AT自动换挡规律的优化相对较少，且多采用Cruise软件优化. 倪计民，周良锋使用Cruise软件建立模型，对公交客车的换挡规律进行优化[1-2]. 赵璐对商用车AMT运用Cruise软件进行了最佳燃油经济性换挡规律优化计算[3]. 钟鑫针对某些工况发生频繁换挡、错误换挡的现象，对公交车液力机械自动变速器综合性换挡规律进行了智能修正[4]，但其方法较复杂，不具有普遍性. 文献[5]提出一种换挡图设计方法，保证了经济性、操纵性、稳健性等. 国内一些高校在该领域取得了一定的成果，葛安林提出了智能换挡的概念并对换挡品质的评价体系进行了完善[6]. 赵丁选、龚捷教授的团队对工程车辆建立三参数、四参数换挡规律以及进行了自适应神经网络自动换挡控制、模糊控制等的研究[7-9]. 于涛、魏巍等对高速军用推土机进行了换挡规律和换挡品质的优化[10-11]. 席军强、陈慧岩等提出一种换挡规律逆向试验解析方法[12]. 文献[13]应用Cruise对AMT的经济性换挡规律进行了优化和仿真. 张炳力对叉车建立了基于车速和油门开度的动力性换挡规律，并针对坡道工况采用模糊控制对换挡规律输出的理论挡位进行修正[14].

文中设计了基于车速与油门开度的组合型动力性换挡规律，利用MATLAB /Simdriveline 基于模块化建模方法，建立了某矿用汽车的仿真模型，并进行仿真分析. 所建模型用于对换挡规律的研究分析，通过仿真结果确定换挡规律的可靠性、有效性和控制器控制功能是否达到预先设定的要求. 之后应用ISIGHT优化软件，联合MATLAB 对换挡规律进行协同仿真优化设计. 该方法简单有效，适用性强.

1 动力性换挡规律设计

文中采用组合型动力性换挡规律，油门开度大于40%时为基于车速和油门开度的双参数换挡规律，低于40%时为基于车速的单参数换挡规律. 最佳动力性换挡特性通常以相邻两挡在换挡过程中各油门开度下牵引力与车速的关系、加速度与车速的关系来描述[15].

换挡规律求解过程用到的主要参数如表1.

表1 计算参数

由于其中涉及到液力变矩器的闭解锁问题，提出下面的闭解锁策略.

(1)1 挡不闭锁，为全液力工况；2挡进行闭解锁控制；3到6挡全为机械工况.

(2)换挡过程解锁，利用液力元件的缓冲作用改善换挡品质.

(3)为了保证不频繁的闭锁解锁，解锁车速相对于闭锁车速有一定的延迟.

(4)油门开度低于30%时不闭锁.

换挡规律计算具体流程如下.

(1)根据发动机净外特性和调速特性、液力变矩器原始特性计算发动机与变矩器共同工作输入、输出特性.

(2)根据公式(1)分别计算液力工况和机械工况各油门开度下各挡加速度.

(1)

式中：m为车辆质量，kg；δ为汽车旋转质量换算系数；du/dt为行驶加速度，m/s2；Ttq为发动机转矩，Ν·m；ig、io为变速器、主减速器传动比；ηT为传动系的传动效率；r为车轮半径，m；Ff、Fi、Fw为滚动阻力、坡度阻力和空气阻力，N.

(3)作1、2挡液力工况，2～6挡机械工况加速度曲线.

(4)求各油门开度下各挡位加速度曲线交点，即为升挡点. 根据闭解锁规律，1挡升2挡换挡点为其液力工况加速度曲线交点；2挡以上的换挡点为相应挡位机械工况加速度曲线交点.

(5)根据降挡速差确定降挡点. 目标车辆为重型车辆，所以降挡速差设计为如下形式：大油门开度时的降挡速差较小，因而在大油门开度时升降挡都能保证较好的功率利用，动力性好；小油门开度时的降挡速差较大，可使换挡次数减少，而且发动机以较低转速运转，燃料经济性好，噪音小，行驶平稳舒适. 低挡位时,为保证车辆动力性，降挡速差较小；高挡位时,降挡速差较大，保证车辆在很大的车速范围内使用高挡而不降挡，减少换挡次数，提高动力和经济性能. 求得动力性换挡规律如图1.

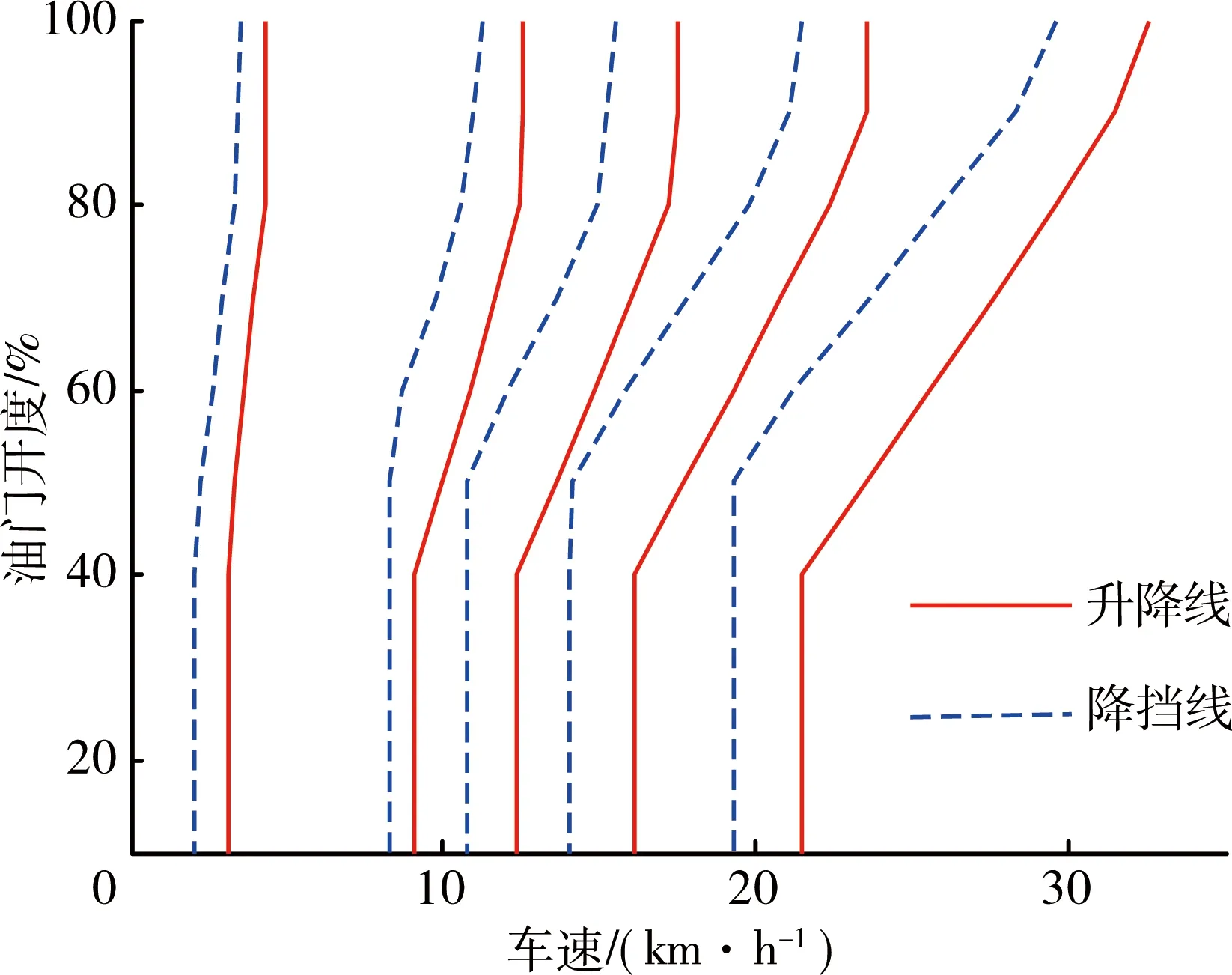
图1 动力性换挡规律曲线

2 动力学建模及仿真

2.1 动力学模型

车辆动力学系统是一个多领域系统，由属于机械、液力以及控制工程等领域的子系统如发动机、齿轮变速机构、液压转向机构、液力变矩器、离合器控制系统、地面阻力系统等组成，是一个复杂的机、电、液混合的多自由度、时变的动态系统，需要对车辆进行准确的动力学建模. 现在一般采用模块化建模方法，可以大大减轻建模工作量，有利于各个子系统的封装与移植[16].

文中运用物理建模软件MATLAB/SimDriveline建立整车模型，如图2.包括发动机、液力变矩器、行星齿轮机构、地面阻力、控制器等子模块.

图2 整车动力学模型

2.2 仿真结果及分析

为了确定换挡规律的动力性、合理性，针对以上设计的换挡规律，进行最大油门开度下连续升挡的动力学仿真.

取发动机油门开度为100%，整车质量m=1.2×105kg，仿真结果如图3、图4所示，图3中1代表变矩器闭锁，0代表变矩器解锁.

图3 挡位、闭解锁信号与冲击度变化曲线

根据仿真结果，可以看出仿真模型实现了升挡过程的仿真，且转速变化曲线与实测数据相符. 图3中挡位和闭解锁信号的变化表明仿真模型实现了设计的变矩器闭解锁控制，闭解锁动作与换挡动作协调. 图4为采用设计的换挡规律与采用其他换挡点时仿真得到的车速对比曲线.可以看到前者曲线更平滑，加速也更快，验证了换挡规律的合理性和优越性.

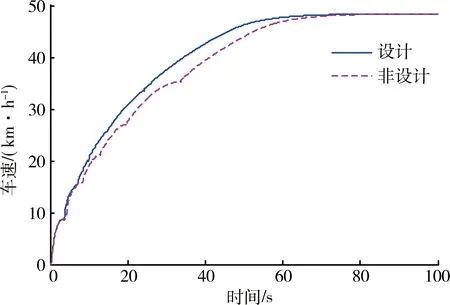
图4 设计与非设计换挡规律下的车速对比曲线

采用设计的换挡规律仿真时，车速由0加速到32km/h用时21.5s；而采用非设计换挡点仿真时,加速时间为25s. 可以看出，设计的换挡规律加速性更好.

现以3挡升4挡为例，介绍换挡过程及离合器和制动器油压变化.3挡结合的离合器为C1和B2，4挡结合的离合器为B1和B2. 故换挡过程中B2始终结合，C1由结合变为分离，而B1由分离变为结合. 图5为3挡升4挡过程中闭锁离合器CL，离合器C1和制动器B1，B2的油压变化.

图5 3挡升4挡离合器油压变化仿真曲线

由仿真结果看出:8s时(此时为3挡),液力变矩器闭锁，由液力工况变为机械工况；9.7s时,达到升挡车速，升为4挡，升挡的同时液力变矩器解锁，此时制动器B1油压升高，闭锁离合器CL和离合器C1油压降低到0，B2油压保持不变，11.2s时,液力变矩器再次闭锁，CL结合，从而由液力工况变为机械工况. 仿真结果中,油压的变化符合换挡逻辑，并与图6中的实车试验结果相符.

图6 实车试验时3挡升4挡离合器油压变化曲线

3 换挡规律优化

根据数据求出的换挡规律,只是理论上最优的结果.由于模型具体的换挡策略,以及换挡规律求曲线交点存在误差等因素,可能所求得的换挡规律在实际应用中并不是最优解，因而文中采用ISIGHT联合所建的Simulink模型对所求换挡规律进行优化，以得到实际运行中最优的换挡规律点.

优化流程如图7.

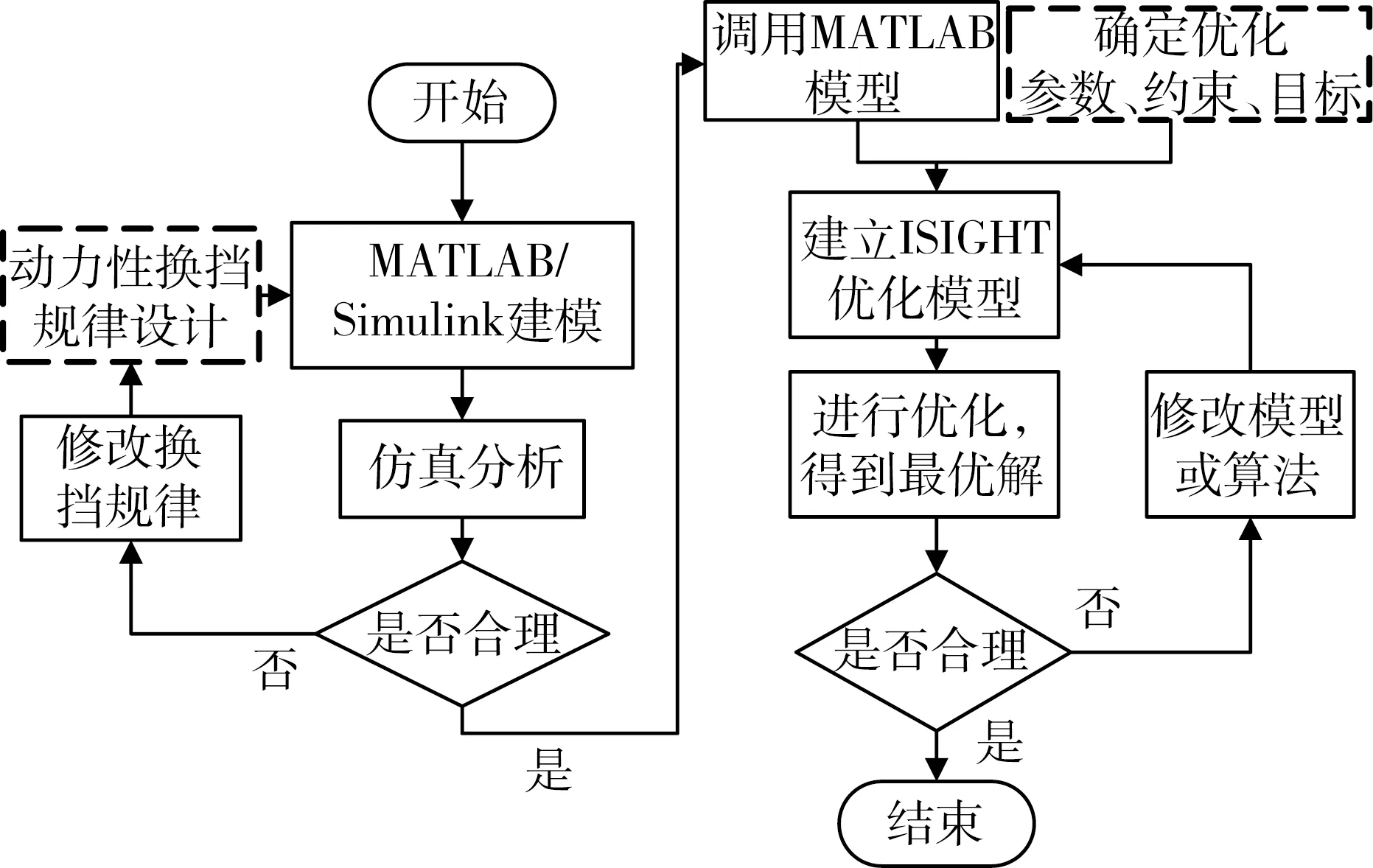
图7 优化设计流程图

优化原理为：在ISIGHT中定义优化变量、优化目标、优化约束，并赋予变量以初值，作为MATLAB模型的输入，MATLAB运行的结果作为输出，ISIGHT优化算法根据输出结果修正优化变量,并作为输入不断调用MATLAB，直至获得理想性能. 如图8.

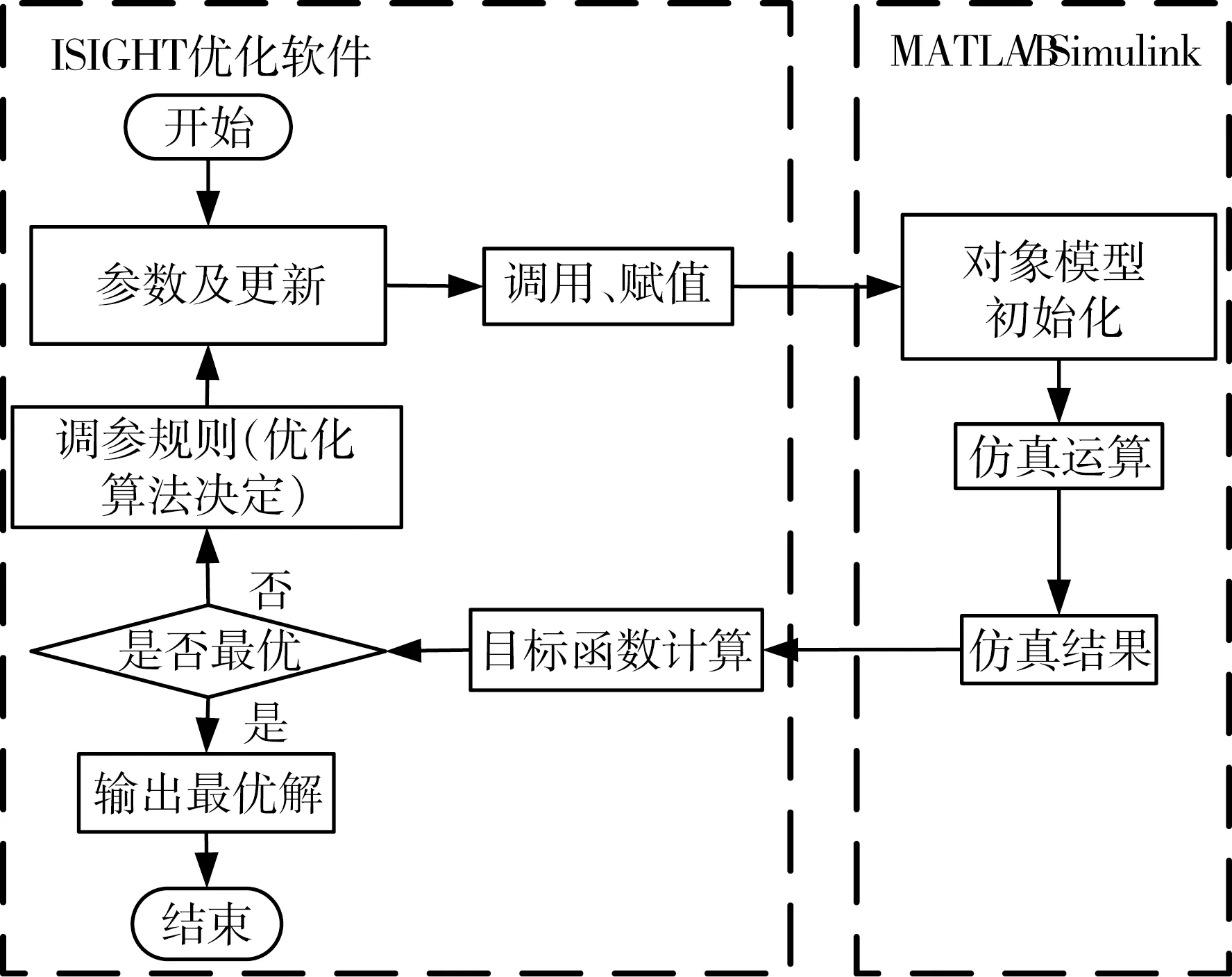
图8 优化原理示意图

汽车的动力性评价指标有最高车速、加速时间、最大爬坡度，最高车速和最大爬坡度主要与发动机参数、传动比、汽车质量、汽车阻力等因素有关，与换挡规律无关，只有加速时间与换挡规律有关.所以选取加速时间为优化目标.

3.1 优化问题描述

1)设计变量：100%，70%，50%油门开度下，挡位由1挡依次升到6挡时，车速依次设为v1、v2、v3、v4、v5.

2)以动力性为目标，目标函数为：动力性目标(全油门开度下0～32 km/h加速时间最短)

(2)

3)约束条件：考虑各挡最高、最低车速和降挡速差等因素，确定各挡升挡车速范围如下.

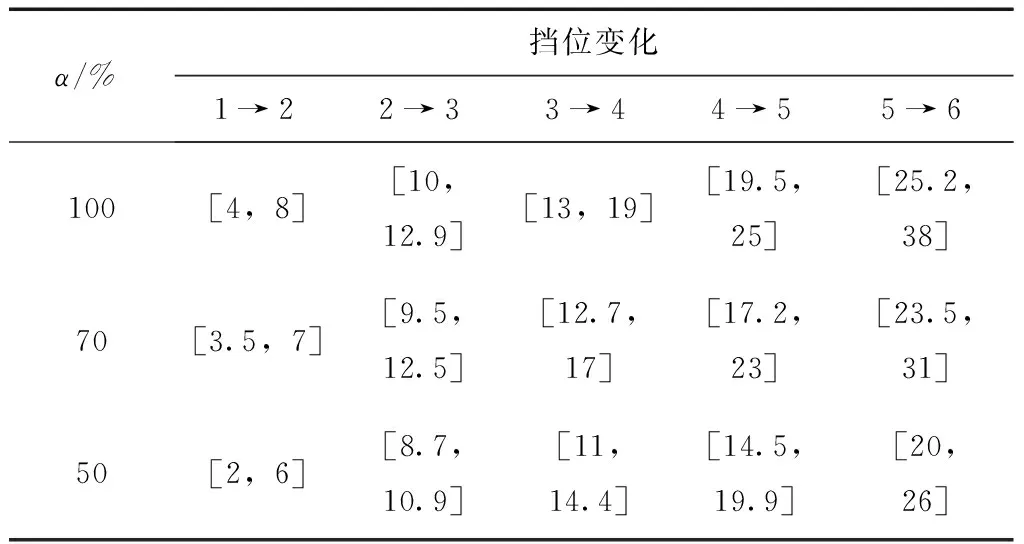
表2 升挡车速范围 km/h

3.2 优化模型

分别对每个油门开度单独优化. 以100%油门开度为例，用ISIGHT软件建立优化模型. 优化过程中，Optimization模块作为优化器，调用性能仿真软件并赋值优化变量v1、v2、v3、v4、v5，性能仿真软件MATLAB相当于一个求解器，根据新的输入参数，通过command中的m文件调用所建的Simulink模型完成整车仿真，并将仿真结果tac提供给Optimization模块，Optimization模块根据相应算法调整优化变量，并重新赋值给MATLAB，如此循环直至获得理想性能. 图9为ISIGHT中所建模型的数据交换图.

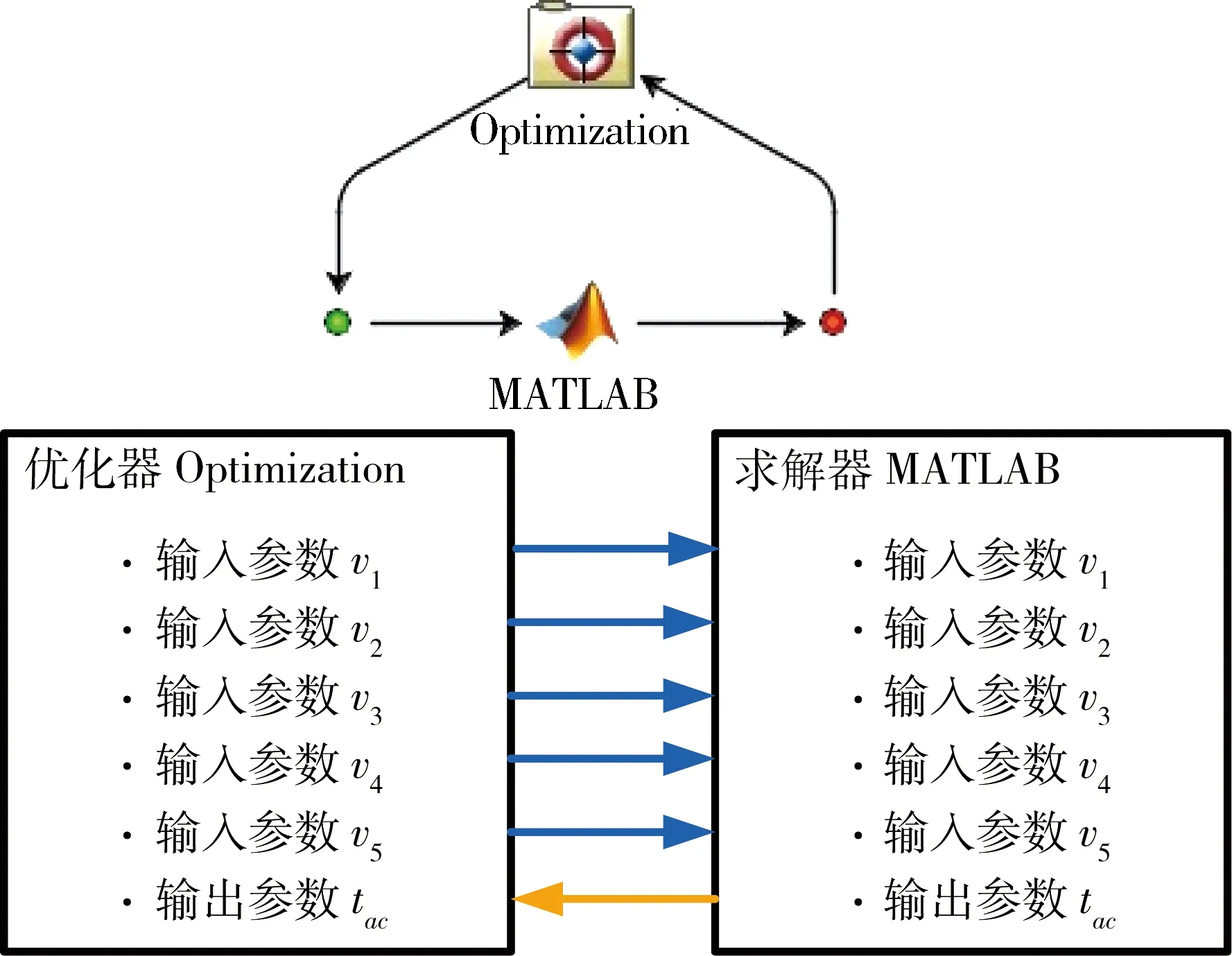
图9 优化模型的数据交换示意图

优化模型中，选用多岛遗传算法(Multi-islandGA)进行优化. 多岛遗传算法Multi-islandGA是经过改良的遗传算法，主要特点是把整个种群分成若干个子种群，在每个子种群中进行传统遗传算法的所有操作，并且在每个子种群中选定一些个体定期地迁移到另外的岛上，然后，继续进行遗传操作. 通过这种迁移操作可以维持群体的多样性，能更有效的搜索全局解空间的最优解[17].

3.3 优化结果与分析

以100%油门开度为例，优化过程共有1001步，在第382步达到最优. 将最优解与优化前进行对比，如表3.

表3 升挡点优化前后参数对比 km/h

可以看到，优化后加速时间降低，动力性有所改善. 同时比较优化前后换挡点，可以看出优化后的升挡点均比优化前的升挡点提前，这是由于动力学模型的Stateflow模块中，为避免换挡重叠，采取了2 s的换挡延迟.

4 结 论

针对某重型矿用汽车，设计了基于车速和油门开度的双参数动力性换挡规律，并搭建MATLAB/Simulink仿真模型进行仿真分析. 仿真结果表明，所设计的换挡规律具有较好的动力性. 以加速时间为优化目标，运用ISIGHT优化软件对100%、70%、50%油门开度下的升挡点进行优化. 通过优化得到加速时间最优的换挡规律，提高了动力性. 优化结果表明，该方法对换挡规律设计和改进有实际意义.

[1] 倪计民，邬立波，周 艳，等. 基于DOE的公交客车换挡规律优化[J].车用发动机，2011(6)：28-32.

[2] 周良锋，郭仲海.基于Cruise的AMT汽车换挡规律仿真分析与优化[J]. 农业装备与车辆工程，2011(4)：37-42.

[3] 赵 璐，卢新田.商用车AMT自动换挡规律的优化设计[C]//2013中国汽车工程学会年会论文集.北京：北京理工大学出版社，2013：778-782.

[4] 钟 鑫. 公交车液力机械式自动变速器换挡规律的研究与优化[D].长沙：湖南大学，2013.

[5] Viet Dac Ngo, Theo Hofman, Maarten Steinbuch. Gear shift map design methodology for automotive transmissions [J]. Automobile Engineering，2014，228(1)：50-72.

[6] 葛安林，金 辉，张洪坤，等．一种汽车智能换挡体系的研究[J]．中国机械工程，2001(5)：106-109.

[7] 崔功杰，赵丁选．动态四参数工程车辆的自动换挡规律[J].西安交通大学学报，2008，42(9)：1189-1192.

[8] 鲍金锋.工程车辆新型三参数换挡规律的研究[D]. 长春：吉林大学，2011.

[9] 康怀亮.工程车辆三参数动力节能换挡规律研究[D].长春：吉林大学，2012.

[10]于 涛. 高速军用推土机换挡与效率控制研究[D].北京：北京理工大学，2014.

[11]WU Jing-yan, WEI Wei, QU Jing-yao. Optimization Design of Double-parameter Shift Schedule of Tracked Vehicle with Hydrodynamic—mechanical Transmission[J]. Journal of China ordnance，2011，7(3)：135-139.

[12]胡宇辉，杨 林，席军强，等. 某单轴并联混合动力客车换挡规律的解析[J].汽车工程，2013，35(7)：629-634.

[13]Xiong Guangming, Xi Junqing, Zhang Yan, et al. Optimal design and simulation evaluation of economical gear-shiftingschedule for AMT in pure electronic bus[C]// Industrial Technology (ICIT), 2010 IEEE International Conference on.[S.l.]:IEEE,2010:1131-1135.

[14]张炳力，胡福建，董彦文.叉车自动变速器控制系统的设计[J].农业工程学报，2012，28(5)：66-71.

[15]卢德琼. 汽车自动变速器建模和换档规律的研究[D] .武汉：武汉理工大学，2006.

[16]周云波. 基于MATLAB/SimDriveline的某型军用车辆起步过程仿真研究[J]. 南京理工大学学报，2011，35(4)：507-512.

[17]沈忠亮，陈 剑，蒋丰鑫. 改进的多岛遗传算法在动力总成悬置系统优化设计中的应用[J]. 噪声与振动控制，2014，34(6)：79-84.

Design and Optimization of Shift Schedule for a Mining Truck

ZHANG Xiao-cong， SUN Liang， WANG Wei-da， YAN Qing-dong

(National Key Lab of Vehicular Transmission，Beijing Institute of Technology，Beijing 100081，China)

In order to improve its dynamic performance, a shift schedule is designed for a mining truck. A dynamics model of the vehicle is established by MATLAB/Simdriveline, and its performance is verified by using the designed schedule. In order to get the optimal shift points for the model, the method is put forward of taking the acceleration time as a goal and optimizing every shift point in ISIGHT and MATLAB. The vehicle performance of using the optimized schedule is compared with that of the designed one. The simulation results show that, with the optimized shift schedule, the acceleration time of the vehicle reduces and the performance gets better. This method can be used to modify the optimization variables, the shift schedule and the simulation parameters．

mining truck; shift schedule; optimization; modeling and simulation

1009-4687(2015)04-0008-06

2015-9-20

张晓聪(1990-),女,研究方向为自动变速器换挡规律设计.

TJ811

A