复合传动动力舱AHP模糊综合评价方法
田 园, 潘宏侠,2, 张 媛, 曹满亮
(1.中北大学 机械与动力工程学院, 太原 030051; 2.中北大学 系统辨识与诊断技术研究所, 太原 030051;3.中国电子科技集团第二研究所, 太原 030024)
复合传动动力舱AHP模糊综合评价方法
田 园1, 潘宏侠1,2, 张 媛3, 曹满亮1
(1.中北大学 机械与动力工程学院, 太原 030051; 2.中北大学 系统辨识与诊断技术研究所, 太原 030051;3.中国电子科技集团第二研究所, 太原 030024)
针对某型装甲车辆机电复合传动动力舱多指标、多层次综合评价问题,建立了一种层次分析模糊综合评价方法.采用专家意见法构建复合传动系统指标体系,根据业内专家构建底层指标模糊评价矩阵,并运用层次分析法拟定每层指标权重,并进行一致性检验;底层评价结果即作为上层模糊评价矩阵,依据对应层权重实施评价,获得此层评价结果.逐次运算直至最顶层,获得传动系统评价量化结果及结论.并以某型装甲车辆动力舱为例对其有效性进行了验证.结果表明:该模型对各项指标进行综合评价是有效可行的.
复合传动动力舱;专家意见法;层次分析法;模糊综合评价
动力舱是坦克装甲车辆的核心部分,其组成包括动力、传动及辅助系统,占整车体积较大比例,对整车性能,尤其对机动性能的发挥起着决定性作用.新一代坦克装甲车辆采用属于混联式混合动力的机电复合传动(electro-mechanical transmission, EMT).EMT通过机械和电力这两路功率流进行发动机输出能量传递,既充分发挥利用机械功率流传递的可靠、效率高的优点,又能保证发动机工作在效率较高的区域[1].装甲车辆EMT技术涉及到多领域、多学科、多环境、多方面的合作,涉及到机械、动力、电子、控制、材料等多学科的技术知识,同时包含着定性和定量指标,如何合理正确地对其进行评价仍较为复杂.目前,虽然我国装甲车辆发展较快,但对其进行综合评价的研究仍处于起步阶段.董玉才等利用投影寻踪法对装甲车辆武器系统进行综合评价[2];牛庆银等通过Topsis法对坦克柴油机进行评价[3].而针对装甲车辆EMT评价领域的研究不足.因此,提出了利用层次分析及模糊评价的方法,针对装甲车辆EMT进行综合评价,运用层次分析法拟定每层指标权重,将底层评价结果用作上层模糊评价矩阵,依据对应层权重进行评价.以此类推到最顶层,最终得出评价结果.
1 评价方法选择
近些年,随着多指标综合评价研究的不断深入,相关领域的诸多知识随之渗入,不断丰富并完善着多指标综合评价方法,目前已经取得了长足的进步.美国匹兹堡大学教授、运筹学家T.L.Saaty首次提出了一种定量、定性相结合的、层次化、系统化的分析方法——层次分析法(analytic hierarchy process, AHP)[4],其分析过程流程图如图1所示.为了解决模糊的、难以量化的、非确定性的问题,美国自动控制专家L. A zadeh教授首次提出了模糊综合评价法(fuzzy compositive evaluation, FCE),这属于一种基于模糊数学的综合评价方法,可以根据模糊数学的隶属度理论将定性评价转化成定量评价,即针对受到多种因素制约的事物,利用模糊数学对其做出一个总体的评价[5].该方法具有系统性强、结果清晰的特点.
对于复杂的机电复合传动动力舱,由于参数类型各异、测试信号繁多,同时存在着定性指标和定量指标,单纯采用AHP法无法摆脱认识上的模糊性,以及评价过程中的随机性和专家主观上的不确定性,因而并不能全面衡量机电复合传动动力舱的综合性能.因此,采用将层次分析法与模糊理论相结合的方法来对机电复合动力舱进行综合评价,以保证评价的科学性、全面性.
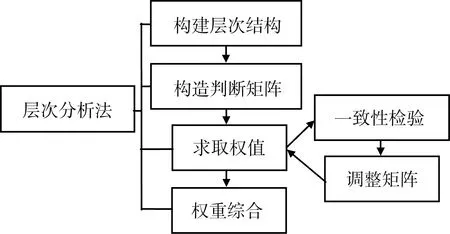
图1 层次分析法流程图
2 层次分析模糊综合评价模型
2.1 指标体系的建立
针对系统各项性能指标进行分析,对评价指标体系进行初步拟定之后,采用专家意见法对指标体系进行选取、修改并完善.设邀请了P位领域专家进行评议,所拟定的指标体系中有g个指标构成了指标体系中的某层[6].定义专家意见集中度为:
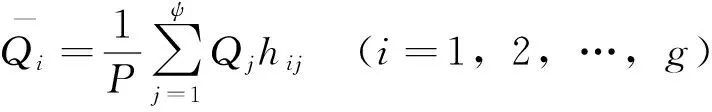
(1)
定义专家意见离散度为:
(2)
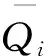
2.2 因素集和评语集的确定
评价对象评价因素的集合称为因素集,如果有n个因素,表示为U={u1,u2,…,un};不同模糊评定的集合(如优、良、中、差等)称为评语集.可以由实际情况确定评语为m个等级,即表示为V={v1,v1,…,vm}.也可以针对不同的评语进行量化范围划定,目的是使评价结果更为直观[7].
2.3 权重的分配
采用层次分析法进行指标权重分配,步骤如下.
(1)构造判断矩阵.层次分析法的一个显著特征就是利用两两间重要程度之比的形式进行两者间重要性程度等级的表示[8].例如针对某一因素,两两对比其下层的n个指标因素,同时按其重要程度进行等级评定.为避免某一专家对于评价指标赋权的主观性,邀请P位专家对该层各个指标进行两两间的对比打分(1~9分制),将第i和第j个因素的重要性之比记为aij,Saaty给出的重要性等级标度及其取值如表1所示[9].

表1 重要性等级标度表
按两两间的比较结果构建矩阵:
判断矩阵中的aij可以满足如下关系:
(4)
(2)权重向量的计算.为了将有用的信息从判断矩阵中提取出来,为科学的综合评价提供依据,则需要进行判断矩阵权重向量的计算.对判断矩阵A,若∀aij=aikakj(i,j,k=1,2,…,n),则A满足一致性并成为一致性矩阵.一致性矩阵A满足:rank(A)=1,且特征值λmax=n唯一,其规范化特征向量W=(w1,w2,…,wn),称为权重向量,且aij=wi/wj.所以,对于构建出的判断矩阵,通过求出最大特征值所对应的特征向量并规范化进而可以求出权值[10].
(3)一致性检验.在实际操作过程中,由于领域专家在进行两两比较时的定级技巧和价值取向以及重要程度等级赋值产生的非等比性,判断矩阵阶数大于2时,通常构建出满足一致性的矩阵较为困难.但对于判断矩阵来说,其偏离一致性条件应在一定范围内,因而必须鉴别判断矩阵是否可接受,这就需要进行一致性检验[11].由于A=(aij)m×n满足aij>0,aij=1/aji,aii=1,所以,A=(aij)m×n为正互反矩阵,其最大特征值λmax≥n,当且仅当A为一致性矩阵式等号成立.则可根据λmax是否等于n来进行矩阵一致性的检验,若λmax相比n大很多,证明A偏离一致性的程度越严重.因而一致性指标定义为
(5)
定义平均随机一致性指标RI,如表2所示.

表2 平均随机一致性指标标准值表
一致性比率(CR)为一致性指标(CI)与随机一致性指标值(RI)之比,即
(6)
若CR<0.1,则证明该判断矩阵满足一致性检验要求,证明权重分配合理可行;若CR≥0.1,则需要对判断矩阵进行调整,直至其能够通过一致性检验[12-13].
2.4 模糊评价矩阵(隶属度矩阵)的建立
评语集:V={v1,v2,…,vm},隶属度向量:Ri={ri1,ri2,…,rim},i=1,2,…,n,各个评价主体对某一特定指标因素ui(i=1,2,…,n)做出评价vj(j=1,2,…,m)的可能性大小即为隶属度rij.由隶属度向量Ri得出该层评价指标集的模糊评价矩阵为[14]:
(7)
2.5 模糊评价向量的计算
评价结果计算式为
(8)
得出评价结果Y=(y1,y2,…,ym).
把位于最底层(n层)得出的评价结果合成作为该层上一层(n-1层)的模糊评价矩阵,再以第n-1层的权重为依据算出其评价结果;之后把第n-1层的评价结果构成第n-2层的模糊评价矩阵,然后依据第n-2层权重进行评价结果计算;依此方法计算直到最顶层.
还可以将评语集中各个元素进行量化,例如设V={v1,v2,…,vm}={100,75,50,25},得到最终评价结果:
(9)

3 实例分析
3.1 构建综合评价指标体系

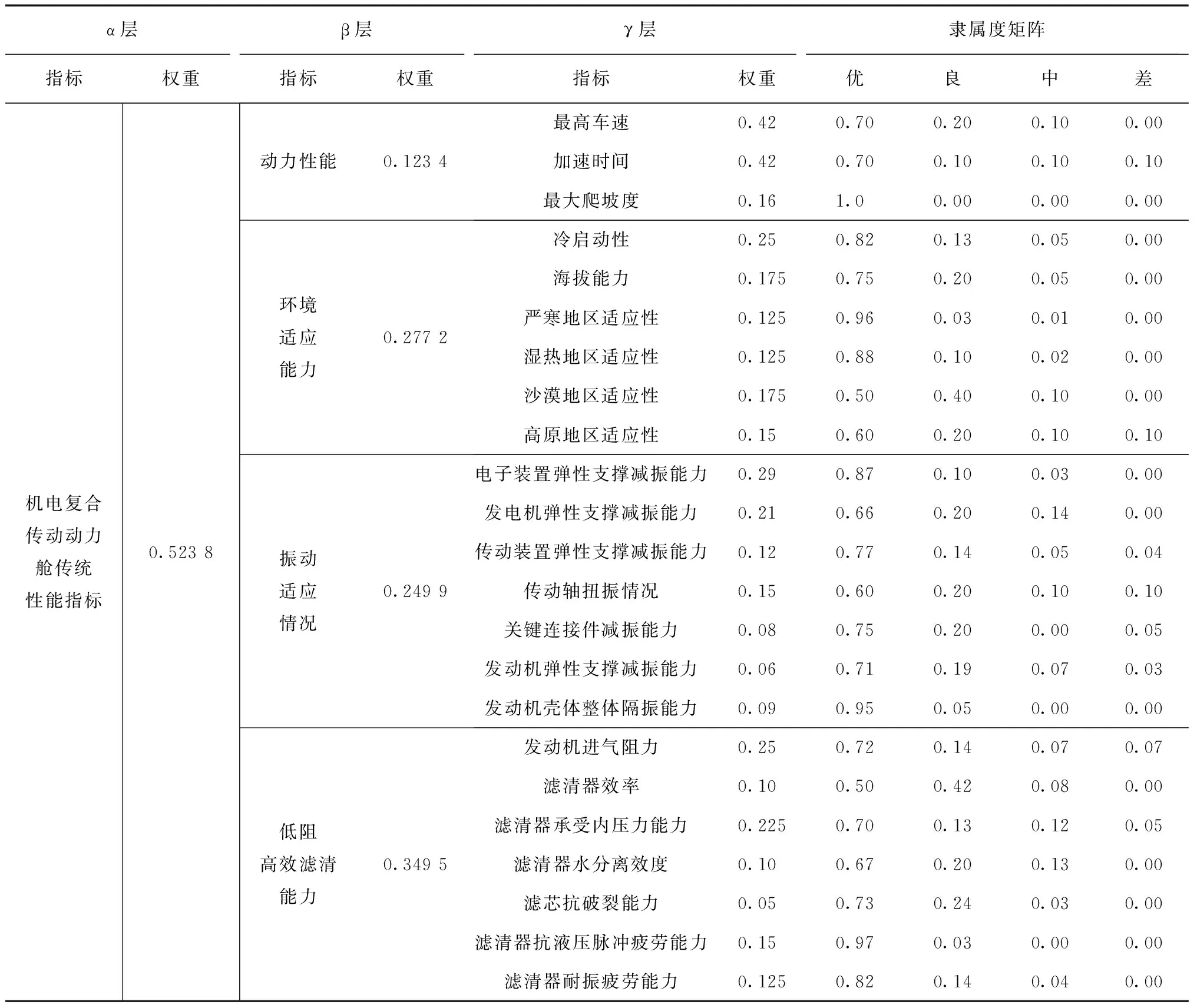
表3 机电复合传动动力舱传统性能指标体系

表4 机电复合传动动力舱革新性能指标体系
3.2 确定指标权重
3.2.1α层指标权重
经归一化得到权重向量:wα=(0.523 8,0.476 2).
由于判断矩阵阶数为2,不需要进行一致性检验.
3.2.2β层指标权重
(1)传统性能指标β层判断矩阵
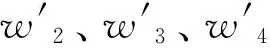
经归一化得到权重向量:
(0.123 4,0.277 2,0.249 9,0.349 5).
Aβ的最大特征根为λmax=4.
查表2得:n=4时,RI=0.893 1.
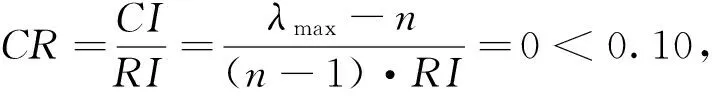
(2)革新性能指标β层判断矩阵
同理可求出权重向量:
4.1 结论 以杭州龙井品牌为例对农业品牌真实性、网络口碑和顾客价值共创意愿之间的关系进行了初步的研究,主要的结论有以下几点。
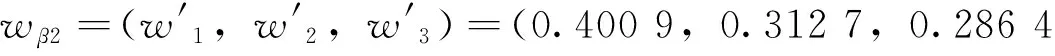

图2 动力舱β层各项指标总权重
3.2.3γ层指标权重
γ层的指标权重计算步骤与α层及β层相同,计算得到:
wγ1=(0.42,0.42,0.16),
wγ2=(0.25,0.175,0.125,0.125,0.175,0.15),
wγ3=(0.29,0.21,0.12,0.15,0.08,0.06,0.09),
wγ4=(0.25,0.10,0.225,0.10,0.05,0.15,0.125),
wγ6=(0.27,0.11,0.21,0.12,0.05,0.07,0.06,0.11),
wγ7=(0.13,0.13,0.13,0.17,0.20,0.17,0.07). 过程不再赘述,最终得到表3、表4所列出的“γ层指标权重”.
3.3 确定模糊评价矩阵
邀请到了10位专家,分别针对最底层每一个评价因素进行等级评定,获得γ层模糊评价矩阵Rγ1~Rγ7.详见表3、表4.

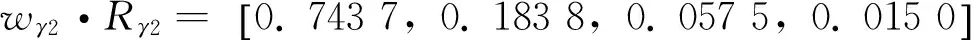
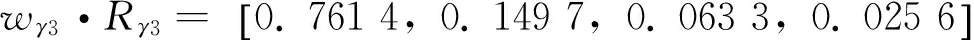
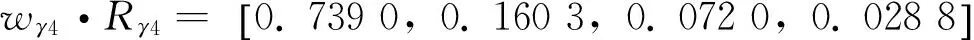
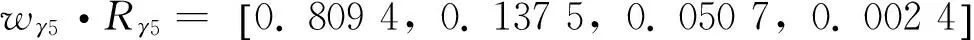

3.4 确定多层模糊评价矩阵
3.4.1β层模糊评价矩阵

3.4.2α层模糊评价矩阵
得到评价结果:

3.5 确定因素集及评语集


4 结 论
在装甲车辆EMT综合评价方面,完善的评价机制仍未真正建立,合理准确的评价标准的确定尚处初探阶段,评价决策体系仍未成形.本文采用的层次分析模糊评价方法能够对信息呈模糊性的EMT指标做出科学合理的量化评价,同时将科学计算与专家经验相结合,兼具进一步加工性,为EMT综合评价提供了切实可行的方法.该方法确定指标权重时,仍具有一定的主观性,所以需要对具体某型号系统进行深入分析后,进行参数的合理选取,从而使评价结果合理、科学.
[1] 臧克茂,廖自力,李 华. 坦克装甲车辆电传动总体技术的研究[J]. 车辆与动力技术,2007(1):5-12.
[2] 董玉才,范格华,张 玲,等. 基于投影寻踪法的现代主战坦克武器系统综合评价[C]//2011年青年通信国际会议论文集.北京:国防工业出版社,2011:281-283.
[3] 牛庆银,袁 义,牛庆银,等. 基于Topsis法的坦克柴油机整机性能综合评价[J]. 信息系统工程,2011(12):112-113.
[4] 谢化勇,肖明清,方甲永,等. 自动测试系统多层次模糊综合评价方法[J]. 火力与指挥控制,2012,37(7):102-106.
[5] 董玉才,范格华,张 玲,等. 基于投影寻踪法的坦克动力舱热工况综合评价[J]. 数学的实践与认识,2011,41(17):157-161.
[6] 邓 雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究[J].数学实践与认识,2012,42(7):94-100.
[7] 夏 萍,汪 凯,李宁秀,等.层次分析法中求权重的一种改进[J].中国卫生统计,2011,28(2):151-156.
[8] 杨化动,苏 慧.齿轮箱减速器设计方案模糊评价方法的研究[J].机械设计与制造,2009,2(2):53-55.
[9] 傅金祥,陈 喆,马新冠,等.改良模糊综合评价法在水质评价中的应用[J].环境工程,2011,29(6):120-125.
[10]张永民,李 鹏.员工绩效模糊综合评价法[J].中外企业文化,2009,12(3):57-59.
[11]刘海涛,郁新德.基于AHP的企业组织绩效模糊综合评价[J].技术与创新管理,2011,32(2):160-165.
[12]牛印宝,汪永超,王 宁.面向绿色制造的刀具评价方案的研究[J].组合机床与自动化加工技术,2014,10(8):1-4.
[13]MaZhongying,YangQi,ZhouWei.Comprehensiveevaluationmodelforruralroadbasedonfuzzydefinition[J].ChinaJournalofHighwayandTransport,2010,23(5):102-106.
[14]Jitrawichawet,Supawadee,Sarfaraz.Reliabilitybasedforeignsupplierselectionusingfuzzy-AHP[J].InternationalJournalofAppliedDecisionSciences,2013,6(3):245-262.
[15]康 葳,董田沼,杨国振,等.基于AHP的火控系统故障诊断策略研究[J].科技导报,2012,30(13):53-56.
[16]胡 方,黄建国,张群飞.基于层次分析法的鱼雷抗干扰能力评估研究[J].探测与控制学报,2007,29(2):63-66.
AHP Fuzzy Comprehensive Evaluation Method for Power Cabin of Electro-mechanical Transmission
TIAN Yuan1, PAN Hong-xia1,2, ZHANG Yuan3, CAO Man-liang1
(1.School of Mechanical and Power Engineering, North University of China, Taiyuan 030051, China;2.System Identification and Diagnosis Technology Research Institute, North University of China, Taiyuan 030051, China;3.The 2ndResearch Institution of China Electronics Technology Group Corporation, Taiyuan 030024, China)
A fuzzy comprehensive evaluation method with Analytic Hierarchy Process was introduced in view of the problems in the multi-index and multi-level evaluation for its power cabin of an electro-mechanical transmission. The index architecture was built based on the Delphi method, and a fuzzy evaluation matrix with the underlying indexes was constructed according to the knowledge of industry experts. The weight of each index was formulated by using the Analytic Hierarchy Process, and the consistency test was carried out. The evaluation results of the lower level were used as the fuzzy evaluation matrix of the upper one. According to the evaluation of the weight on the corresponding level, the evaluation results of this level were obtained. Successive operations until the top level, the quantitative results and conclusions of evaluating the transmission system were achieved. The validity of the method was verified by an armored vehicle power cabin. The results demonstrated that this model is effective to evaluate various indexes.
power cabin of an electro-mechanical transmission;delphi method;analytic hierarchy process;fuzzy comprehensive evaluation
1009-4687(2015)04-0004-07
2015-10-14
国家自然科学基金“基于粒子群优化与滤波技术的复杂传动装置早期故障诊断研究”(50875247);中国兵器科学研究院委托项目“车动态综合测试与评价技术”(10401)
田 园(1991-),硕士,研究方向为信号识别与处理、装备系统检测与诊断.
TH17
A

