计及多日一充模式的规模化电动汽车充电负荷建模策略

徐 浩 苗世洪 钱甜甜 冉晓洪

(华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074)



计及多日一充模式的规模化电动汽车充电负荷建模策略

徐 浩 苗世洪 钱甜甜 冉晓洪

(华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074)

提出了一种计及多日一充模式的规模化电动汽车充电负荷建模策略，为电动汽车充电负荷预测及有序充电控制措施的制定奠定必要的理论基础。该策略首先依据日行驶里程差异划分了6个用户类，并在详细分析各用户类中单个用户充电起始时刻和充电时长概率特性的基础上，提出了单个用户在指定时刻充电的负荷期望值的计算方法；然后提出了元日期窗口的概念，并分别模拟了两类多日一充模式下各用户类中的用户在元日期窗口内充电的概率分布；最后基于大数定理提出了规模化电动汽车在各工作日内集群充电的总充电负荷计算模型及其离散处理方法。算例分析结果表明，该策略可显著提高规模化电动汽车电池容量的利用率，可获得更为准确的充电负荷特性，且操作性强，因而具有广阔的应用前景。

电动汽车 多日一充 负荷建模 概率特性 大数定理 离散处理方法

0 引言

电动汽车是一种可有效降低温室气体和有害气体排放及化石能源消耗的清洁能源交通工具[1，2]。各国政府和制造商都在大力推动其相关支撑技术的研发和生产，以期缓解当下日益紧张的化石能源短缺和环境污染严重等问题[3-5]。未来电动汽车市场将逐渐趋于繁荣，预计到2020年我国电动汽车累计产销量将逾500万辆[6]。但电动汽车充电功率大、随机性强，如此大规模的保有量将对电网的安全经济运行构成严重威胁[7，8]。因此，有必要研究有效的负荷建模策略，揭示规模化电动汽车的负荷特性及其对电网的影响机制，为充电负荷预测及有序充电策略制定奠定必要的理论依据。

目前，国内外已有大量文献涉及电动汽车充电负荷模型构建问题。文献[9]分析了3种典型电动汽车充电站内用户的充电规律，并构建了基于蒙特卡洛法和统计分析法的充电负荷随机模型。文献[10]在深入挖掘充电负荷影响因素的基础上，提出了充电站内充电负荷的简化计算方式和考虑多种影响因素的准确仿真方法。文献[11-13]基于用户充电起始荷电状态(State of Charge，SOC)与日行驶里程的线性关系，采用汽车用户日行驶里程的详细统计数据构建了大量电动汽车集群充电的概率负荷模型。这些文献从不同的角度分析了规模化电动汽车的负荷特性，所得结论具有丰富的工程参考价值。但上述文献在构建充电负荷模型时，皆假定所有用户必须每天充电一次，以使电动汽车在用户次日第一次出行前处于满电量。该假定通过限制用户充电自由度的方式有效降低了充电负荷模型的复杂度，但将造成电动汽车车载电池容量的极大浪费。因为相关调研数据表明，84.25%的用户日行驶里程小于60 km[14，15]，当电动汽车续驶里程为300 km时，这部分用户的日耗电量仅占车载电池容量的1/5。目前一些电动汽车车型的续驶里程已达300 km，如比亚迪E6和特斯拉Roadster，随着动力技术和电池技术的不断发展，未来电动汽车的续驶里程将超过这个水平。若届时所有用户每天都进行一次充电，无疑将造成车载电池容量利用率的进一步下降。日耗电量超过50%车载电池容量的用户必须每天充电一次，否则将因电池电量不足而影响其次日的正常出行；而同样的调研数据表明，这部分用户所占比例仅为1.8%[14，15]。因此，从提高用户充电自由度和车载电池利用率的角度出发，绝大部分用户不需要每天充电。因此在构建电动汽车集群充电的充电负荷模型时，应当计及用户间隔多日充电一次的情形，以提高所建负荷模型的适用性。

本文拟提出一种计及多日一充模式的规模化电动汽车充电负荷建模策略，将多日一充模式作为部分用户的固有充电模式加以重点考虑，以填补该领域的研究空白。该策略首先依据日行驶里程差异将电动汽车用户分为6个用户类，以使同一用户类中各用户产生的充电负荷可用相同的概率负荷模型模拟。接着提出了单个用户在指定时刻充电负荷期望值的计算法。在此基础上，基于大数定律构建了各用户类中在指定工作日内充电的所有用户集群充电的充电负荷模型。此外，本文提出了元日期窗口的概念，并探讨了各用户类中的用户在元日期窗口内充电的概率分布。在叠加不同工作日内的所有充电负荷后，该策略最终获得了一周内各工作日的总负荷水平。

1 电动汽车用户分类

概率负荷模型是求解规模化电动汽车集群充电总负荷的有效手段。在假定电动汽车用户每天都充电的前提下，各用户具有相同的概率负荷特性，可基于大数定理快速获取规模化电动汽车的总充电负荷[11-13]。为了方便论述，定义每日一充模式为用户在每日的最后一次出行结束后充电的充电模式；定义多日一充模式为用户在日最后一次出行结束后充电且相邻两次充电之间间隔的天数大于零的充电模式。如前所述，在构建充电负荷模型时，应更多地计及多日一充模式。但在考虑多日一充模式后，不同用户相邻两次充电间间隔的天数可能不相同，因而不能用统一的概率负荷模型模拟集群充电中各用户的充电负荷。电动汽车用户分类的目的是将具有相同充电规律的用户归为一类，使各用户类中的所有用户具有相同的概率负荷特性，以方便规模化电动汽车总充电负荷的求解。

通勤和商务用车构成了用户日行驶里程的主要部分[15]。鉴于这两种车辆的使用情况在工作日间基本相同，因此可假定用户在各工作日的日行驶里程恒定不变。用户在节假日间的日行驶里程差异较大，因此节假日的充电负荷需用不同于工作日的充电负荷模型来分析。本文仅考虑工作日的充电负荷模型，节假日的充电负荷模型将在作者的后续工作中体现。依据用户在工作日的日行驶里程，可划分为6个用户类，如表1所示。该表设电动汽车续驶里程为300km。未来电动汽车的续驶里程将超过这个水平，但本文所提充电负荷建模策略仍然适用。表1中，各用户类所占日行驶里程值域空间的上、下限值为

(1)

式中，i=1,2,…,5；hl(Si)和ll(Si)分别为用户类Si所占日行驶里程值域空间的上、下限值；Dev为电动汽车的续驶里程；MCQ(Si)为用户类Si中各用户的最大充电周期(MaximumChargingPeriod，MCQ)，其值如表1所示。此外，hl(S1)=300 km，ll(S6)=0 km。

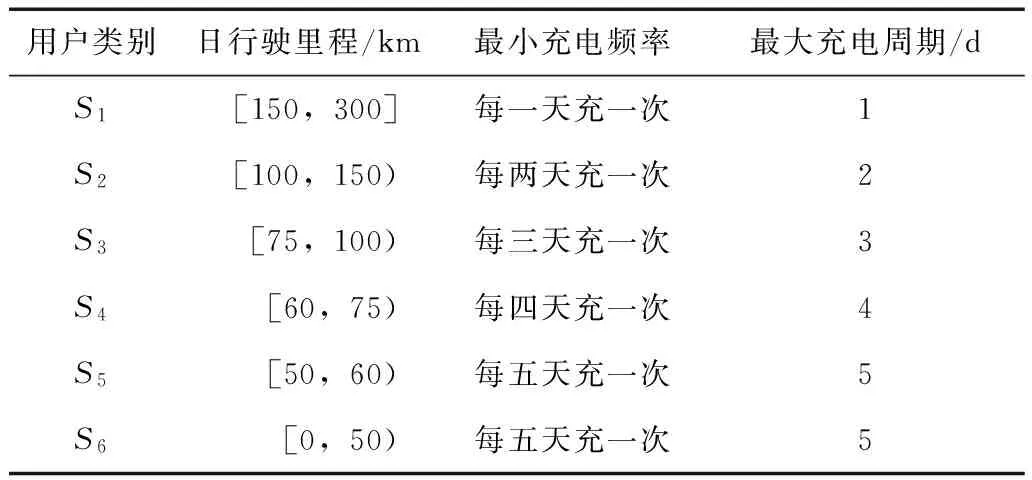
表1 电动汽车用户分类表Tab.1 A classification on electric vehicle users

用户类S5与S6具有相同的最小充电频率和最大充电周期。电动汽车充满一次电后，S5中的用户最多连续使用五天即必须进行二次充电，否则将因电量不足而无法继续行驶；而S6中的用户却可连续使用超过五天。S6中的用户同样须每五天充电一次则是出于所有用户在一周的工作日期间应至少充一次电的假设。

2 各工作日的充电负荷模型

各工作日都有一定数量的用户充电。在求解各工作日总充电负荷的过程中，首先分析单个用户的充电行为，量化单个充电负荷的概率特性，然后提取单个用户的充电负荷期望值，最后基于大数定理求解大量电动汽车集群充电的总负荷。目前电动汽车市场的主要供能设备是锂离子电池，原因在于其在性能、容量、安全性、使用寿命和售价等方面具有较明显优势和较大的发展潜力[16]。本文所有电动汽车都采用锂离子电池供电，因而电动汽车在整个充电周期内都具有恒定的充电功率水平[16]。

2.1 单个用户的充电行为特性分析

电动汽车充电行为具有随机性，主要表现在充电起始时刻和充电时长具有不确定性。分析单个用户的充电随机性有助于求解集群充电的总负荷。需要说明的是，对于某个特定的用户而言，其充电起始时刻等于其日最后一次出行结束的时刻，其充电时长由其日行使里程和充电周期惟一确定，因而其充电行为并不具有随机性[11-13]。这里所提的单个用户是作为规模化电动汽车用户中一个个体而言。由于各用户的充电行为缺乏同步性，规模化电动汽车用户的充电行为因此才具有了随机性。用EVk表示规模化用户的一个个体，则其充电起始时刻、日行使里程及充电时长可取为集群充电中任一用户充电行为特性的对应值，都是随机变量。

假定EVk在时刻t处于充电状态，用Et表示其在该时刻的SOC，则Et是一个变量，其取值范围理论上可达[0，1]。进一步用E0和t0分别表征EVk的充电起始SOC和充电起始时刻，则两者与Et的映射关系为

(2)

式中，C为储能电池的容量；P为电动汽车的额定充电功率；s(Et)为Et的函数，定义s(Et)是为了方便后文式(11)的推导。

在每日一充模式下，E0取值范围理论上可达[0,Et]。对于Et的任何一个特定取值，当E0取[0，Et]范围内的任一数值时，都存在一个t0使式(2)成立。因此Et的每一个特定取值都可由多组不同的E0和t0确定。用φ(E0,t0)表示EVk在时刻t0开始充电且充电起始SOC为E0的概率。由全概率公式可知，EVk在时刻t处于充电状态且SOC为Et的概率可通过累加所有满足式(2)的E0和t0所对应的φ(E0,t0)获得。这种思想同样适用于量化多日一充模式下Et的概率特性。

在对用户分类且计及多日一充模式后，各用户类中单个用户充电起始SOC(即E0)的值域空间不再等于[0，Et]。用τ表示某一工作日，则在τ内充电的用户类Si中单个用户充电起始SOC值域空间的上限值Eh(Si,τ)和下限值El(Si,τ)为

(3)

依据式(3)，可计算出考虑多日一充模式后各用户类充电起始SOC值域空间的上、下限值，如表2所示。该表中，除Eh(S6,τ)外，各Eh(Si,τ)的取值介于0.2～0.5；且除El(S6,τ)外，各El(Si,τ)的取值都为0。由于S6中部分用户在一周的工作日期间完全没有使用电动汽车，因此Eh(S6,τ)高达1。但经过了五天的行驶，S6中工作日期间车辆使用量不为零的用户的充电起始SOC仍低于每日一充时的情形。如引言所述，每日一充模式下84.25%的用户的电池容量使用率都低于20%[14，15]，由此可知在计及用户分类和多日一充模式后，电动汽车车载电池容量的利用率得到明显的改善。

由表2可知，各用户类充电起始SOC的值域空间相互重叠，在建负荷模型时难以分隔开。同时，考虑到不同用户类中的用户所具有的概率负荷特性不同，因此为每个用户类单独构建一个概率负荷模型。用Φ((Et,t,τ)|Si)表示在工作日τ内充电的用户类Si中的单个用户在时刻t处于充电状态且SOC为Et的概率，其计算公式为

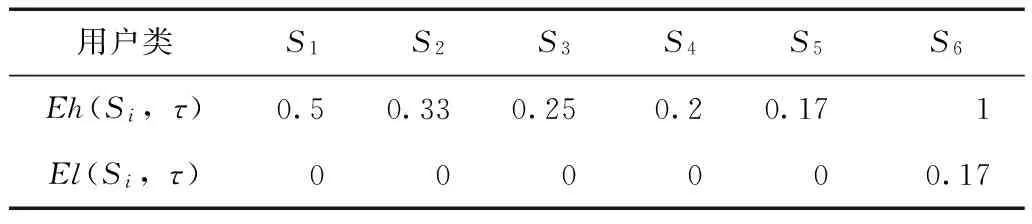
表2 各用户类充电起始SOC值域空间上、下限值Tab.2 Eh(Si，τ) and El(Si，τ) of each user set

(4)

式中，E0,i,τ为在工作日τ内充电的用户类Si中单个用户的充电起始SOC；t0为相应的充电起始时刻，其值依据式(2)计算；φ(E0,i,τ,t0)的含义与φ(E0,t0)一致，为在工作日τ内充电的用户类Si中的单个用户在时刻t0开始充电且充电起始SOC为E0,i,τ的概率。假定充电起始时刻和充电起始SOC二者相互独立，则φ(E0,i,τ,t0)可分解为

φ(E0,i,τ,t0)=k(E0,i,τ)h(t0)

(5)

式中，k(E0,i,τ)为在工作日τ内充电的用户类Si中单个用户充电起始SOC为E0,i,τ的概率；h(t0)为单个用户在时刻t0开始充电的概率。式(5)将一个二维随机变量分解为两个一维随机变量，降低了求解公式的复杂度。同时，基于现有文献给出的关于汽车用户车辆使用习惯的统计数据，可方便的获得k(E0,i,τ)和h(t0)。

假定电动汽车行驶过程中的累积耗电量与行驶里程呈线性关系[11-13]，则充电起始SOC为

E0,i,τ=r(Di)=1-MCQ(Si)Di/Dev

(6)

式中，Di为用户类Si中单个用户的日行使里程；r(Di)为Di的函数，这里定义r(Di)是为了方便后文式(8)的推导。

式(6)表明充电起始SOC与日行使里程具有线性相关性。依据相关统计数据，用户类Si中单个用户的日行驶里程服从概率密度分布[14，15]

(7)

式中，uD=3.47；σD=0.88。参考文献给出的数据以英里为单位，而式(7)已经过单位换算，其距离数据的单位是km。鉴于r(Di)是Di的严格单调函数，由连续型随机变量函数的分布理论可解得k(E0,i,τ)为[17]

(8)

用户充电起始时刻可假定为其日最后一次出行结束时刻。该假定可提高充电便利性、降低忘记充电的概率，且符合用户的充电习惯，因而被许多文献所采纳[14，18，19]。本文采用该假定，并依据相关统计数据，将h(t0)表示为

(9)

式中，μt=17.6；σt=3.4；时刻值采用24 h制。该调查针对的是燃油汽车用户，假定电动汽车与燃油汽车的性能差异不至于影响到用户的行驶习惯，则该调查结果同样适用于电动汽车用户。

2.2 单个用户充电负荷期望值

在工作日τ内充电的用户类Si中的单个用户在时刻t的充电期望值为

(10)

式中，积分因子h(t0)与两个微分因子E0,i,τ和Et缺乏直接关联性，不利于该式的简化计算。为此定义了一个新的概率变量w(Et|(E0,i,τ,t))

(11)

由式(11)可知，w(Et|(E0,i,τ,t))表征的是在充电起始SOC为E0,i,τ且当前时刻为t的条件下Et的条件分布。在充电起始SOC为E0,i,τ且当前时刻为t的条件下，每一对满足式(2)的Et和t0将满足

(12)

将式(12)代入式(10)中可得

(13)

由于k(E0,i,τ)和w(Et|(E0,i,τ,t))的表达式过于复杂，式(13)难以通过解析法直接求解。为方便计算，可进一步对式(13)作离散化处理

μ((P,t,τ)|Si)≈

(14)

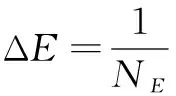
2.3 规模化电动汽车集群充电的总负荷

如前文所述，同一个用户类中各用户所产生的充电负荷可用同一个概率负荷模型模拟，因此可利用大数定理求解任一用户类Si中在工作日τ内充电的所有用户集群充电的总负荷L(Si,t,τ)

L(Si,t,τ)=f(Si,τ)φ(Si)Nsumμ((P,t,τ)|Si)

(15)

式中，f(Si,τ)为用户类Si中的用户在各工作日的概率分布，其值等于用户类Si中在工作日τ内充电的用户数占Si中总用户数的比例；Nsum为研究区域内的电动汽车保有量；i=1,2,…,6。此外，φ(Si)是Si所含用户数量占Nsum的比例，为

(16)

在式(15)的基础上，可进一步解得在工作日τ内t时刻的总充电负荷TL(t,τ)

(17)

式中，Gτ为在工作日τ内充电的用户类集。

2.4f(Si,τ)分布情况的考虑

定义元日期窗口dw(Si)为一周中自周一始至与周一间隔天数为(MCQ(Si)-1)的日期止所涵盖的所有日期；并用ldw(Si)表示dw(Si)内包含的天数。以用户类S3为例：由MCQ(Si)=3可知，ldw(S3)=3， 同时dw(Si)={周一，周二，周三}。 本文中，出于提高电动汽车容量利用率的考虑，各用户按最大充电周期充电，即间隔(MCQ(Si)-1)天充电一次。则用户类Si中的所有用户都将在dw(Si)内充电一次，因此f(Si,τ)可等效为用户类Si中的所有用户在dw(Si)内的数量分布。目前电动汽车仍处于示范运行阶段，与f(Si,τ)相关的统计数据匮乏[18]。本文考虑了f(Si,τ)的两种典型分布，即冲激性分布和均匀随机性分布。为了论述方便，将f(Si,τ)为冲激性分布时的多日一充模式称为第一类多日一充模式；并将f(Si,τ)为均匀随机性时的多日一充模式称为第二类多日一充模式。其中，第一类多日一充模式下f(Si,τ)的表达式为

(18)

式(18)表明，用户类Si中所有用户都将在周一充电。依据各用户类的最大充电周期，可进一步解得第一类多日一充模式下在各工作日充电的用户类，如表3所示。

表3 第一类多日一充模式下在各工作日充电的用户类Tab.3 User sets intending to charging on each weekday under the first multi-day spaced charging mode

第二类多日一充模式下f(Si,τ)的函数表达式为

(19)

3 算例分析

本文以加拿大Manitoba地区为例对本文所提充电负荷建模策略进行算例分析。Manitoba地区目前的汽车保有量为643 580辆[20]；仿真过程将包含电动汽车渗透率为20%和40%两种情形。各工作日的充电负荷按照式(17)计算；其中电动汽车的容量为32kWh，额定充电功率为8kWh。此外，整个仿真过程在Matlab上编程实现。

3.1 第一类多日一充模式下的仿真结果及分析

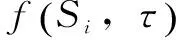
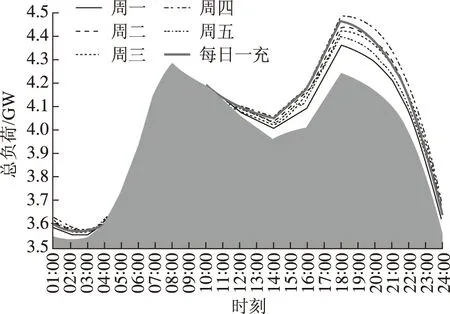
图1 电动汽车渗透率为20%时第一类多日一充模式及每日一充模式下各工作日的日负荷曲线Fig.1 Load curve under the first multi-day spaced and everyday charging mode with an electric vehicle penetration of 20%

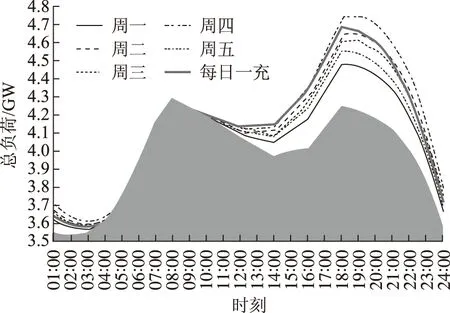
图2 电动汽车渗透率为40%时第一类多日一充模式及每日一充模式下各工作日的日负荷曲线Fig.2 Load curve under the first multi-day spaced and everyday charging mode with an electric vehicle penetration of 40%

表4 第一类多日一充模式及每日一充模式下各工作日的日负荷特性Tab.4 Load characteristics of each workday under the first multi-day spaced and everyday charging mode

图1、图2中，阴影部分的轮廓曲线对应系统的传统负荷曲线，取自Manitoba地区冬季的典型日负荷。由该曲线可知，传统负荷的日波动曲线包含两个负荷尖峰，分别出现在8∶00和18∶00附近，其中，8∶00处的负荷尖峰对应传统负荷的日最大值。传统负荷在23∶00～06∶00之间处于低谷期，这段时间系统吸纳充电负荷的能力最强。当充电负荷较大、该低谷期吸纳能力不足时，传统负荷两个尖峰之间的负荷低凹段(即12∶00～17∶00)也可发挥部分吸纳充电负荷的功效。此外，原始负荷曲线的峰值、谷值、平均值和方差分别为4.28 GW、3.53 GW、3.96 GW和0.06。分析图1、图2和表4，可获得如下结论：

1)充电负荷主要集中在11∶00～24∶00及00∶00～04∶00之间，而在04∶00～11∶00之间的充电负荷基本为零。这说明传统负荷低谷期吸纳充电负荷的能力没有得到充分利用，有必要对规模化电动汽车的充电行为进行有序控制。

2)充电负荷峰值出现在19∶00左右，临近传统负荷的一个尖峰；当电动汽车渗透率较大(20%及以上)时，将显著提高该尖峰值，恶化系统的负荷特性。

3)随着电动汽车渗透率的升高，各工作日的日负荷峰值和日负荷谷值都相应有所提升，同时日负荷峰谷差也随之增加。

4)充电负荷峰值与传统负荷峰值不同步，当电动汽车渗透率超过40%时，部分工作日的系统负荷将在充电负荷峰值处行成新的峰值。例如，当电动汽车渗透率为40%时，周四的日负荷峰值将提高10.75%。

5)在考虑多日一充模式后，各工作日的日负荷曲线不再相同。各工作日按系统负荷峰值由高到低排序依次是周四、周二、周三、周五、周一；这也是各工作日按系统负荷峰谷差和方差由高到低的排序。由此可见，随着充电负荷的增加，系统负荷特性的恶化程度逐渐升高。

6)每日一充模式下的系统负荷水平介于多日一充模式下周三和周四的系统负荷水平之间。换言之，仅考虑每日一充模式获得的充电负荷结果，将低估周四的系统负荷水平，并高估周一、周二和周五的系统负荷水平，造成充电负荷预测及相关控制措施出现差错。

7)随着电动汽车渗透率的升高，每日一充模式下的系统负荷水平与周一和周四的系统负荷水平之间的差距将增加，以至于基于每日一充模式的充电负荷预测结果将出现更严重的差错。

3.2 第二类多日一充模式下的仿真结果及分析

当f(Si,τ)为均匀随机性分布时，在各工作日充电的用户数相等。同样依据式(17)的计算，可获得图3、图4和表5所示的仿真结果。其中，图3和图4分别为电动汽车渗透率为20%和40%时第二类多日一充模式及每日一充模式下各工作日的日负荷曲线；表5为第二类多日一充模式及每日一充模式下各工作日的日负荷特性。其中，这两幅图中阴影部分的轮廓曲线仍为系统的传统负荷曲线。仿真结果表明，第二类多日一充模式下，充电负荷的分布趋势和变化趋势与第一类多日一充模式下的情况一致，这里不另作赘述。此外，图3和图4表明，第二类多日一充模式下的充电负荷水平低于每日一充模式下的充电负荷水平，并且随着电动汽车保有量的增加，两者的差距随之增大。

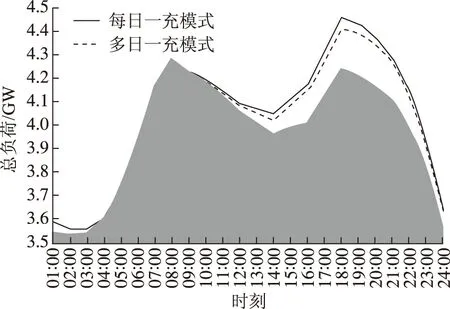
图3 电动汽车渗透率为20%时第二类多日一充模式及每日一充模式下各工作日的日负荷曲线Fig.3 Load curve under the second multi-day spaced and everyday charging mode with an electric vehicle penetration of 20%

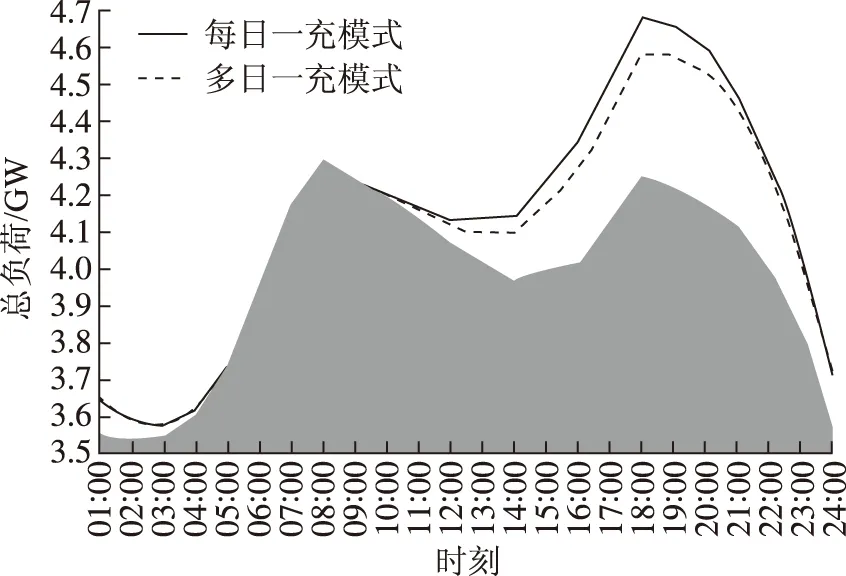
图4 电动汽车渗透率为40%时第二类多日一充模式及每日一充模式下各工作日的日负荷曲线Fig.4 Load curve under the second multi-day spaced and everyday charging mode with an electric vehicle penetration of 40%

4 结论

多日一充模式可提高电动汽车车载电池的利用率，且符合用户的实际充电习惯，应作为部分用户的固有充电模式考虑进规模化电动汽车集群充电的负荷模型中。本文提出了一种计及多日一充模式的规模化电动汽车充电负荷建模策略，填补了该领域的研究空白。算例分析表明，该策略将明显提升了电动汽车车载电池的利用率，并且可获得更为准确的充电负荷特性。

[1] 张学清，梁军，张利，等.计及风光电源的一种地区电网电动汽车充电调度方法[J].电工技术学报，2013，28(2)：28-35. Zhang Xueqing，Liang Jun，Zhang Li，et al.Approach for plug-in electric vehicles charging scheduling considering wind and photovoltaic power in chinese regional power grids[J].Transactions of China Electrotechnical Society，2013，28(2)：28-35.

[2] Peter Richardson，Damian Flynn，Andrew Keane.Optimal charging of electric vehicles in low-voltage distribution systems[J].IEEE Transactions on Power System，2012，27(1)：268-279.

[3] 肖湘宁，温剑锋，陶顺，等.电动汽车充电基础设施规划中若干关键问题的研究和建议[J].电工技术学报，2014，29(8)：1-10. Xiao Xiangning，Wen Jianfeng，Tao Shun，et al.Study and recommendations of the key issues in planning of electric vehicles’ charging Facilities[J].Transactions of China Electrotechnical Society，2014，29(8)：1-10.

[4] 张谦，韩维健，俞集辉，等.电动汽车充电站仿真模型及其对电网谐波影响[J].电工技术学报，2012，27(2)：159-164. Zhang Qian，Han Weijian，Yu Jihui，et al.Simulation model of electric vehicle charging station and the harmonic analysis on power grid[J].Transactions of China Electrotechnical Society，2012，27(2)：159-164.

[5] 曹玲玲，陈乾宏，任小永，等.电动汽车高效率无线充电技术的研究进展[J].电工技术学报，2012，27(8)：1-13. Cao Lingling，Chen Qianhong，Ren Xiaoyong，et al.Review of the efficient wireless power transmission technique for electric vehicles[J].Transactions of China Electrotechnical Society，2012，27(8)：1-13.

[6] 孙晓明，王玮，苏粟，等.基于分时电价的电动汽车有序充电控制策略设计[J].电力系统自动化，2013，37(1)：191-195. Sun Xiaoming，Wang Wei，Su Su，et al.Coordinated charging strategy for electric vehicles based on time-of-use price[J].Automation of Electric Power Systems，2013，37(1)：191-195.

[7] 杨冰，王丽芳，廖承林.大规模电动汽车充电需求及影响因素[J].电工技术学报，2013，28(2)：22-27. Yang Bing，Wang Lifang，Liao Chenglin.Research on power-charging demand of large-scale electric vehicles and its impacting factors[J].Transactions of China Electrotechnical Society，2013，28(2)：22-27.

[8] 田文奇，和敬涵，姜久春，等.电动汽车充电负荷空间分配优化算法[J].电工技术学报，2013，28(3)：269-276. Tian Wenqi，He Jinghan，Jiang Jiuchun，et al.Electric vehicle charging load spatial allocation optimization algorithm[J].Transactions of China Electrotechnical Society，2013，28(3)：269-276.

[9] 杨波，陈卫，文明浩，等.电动汽车充电站的概率负荷建模[J].电力系统自动化，2014，38(16)：67-73.Yang Bo，Chen Wei，Wen Minghao，et al.Probablistic load modeling of electric vehicle charging stations[J].Automation of Electric Power Systems，2014，38 (16)：67-73.

[10]杨少兵，吴命利，姜久春，等.电动汽车充电站负荷建模方法[J].电网技术，2013，37(5)：1190-1195. Yang Shaobing，Wu Mingli，Jiang Jiuchun，et al.An approach for load modeling of electric vehicle charging station[J].Power System Technology，2013，37(5)：1190-1195.

[11]Staats P T，Grady W M，Arapostathis A，et al.A statistical method for predicting the net harmonic currents generated by a concentration of electric vehicle battery chargers[J].IEEE Transactions on Power Delivery，1997，12(3)：1258-1266.

[12]Qian Kejun，Zhou Chengke，Allan Malcolm，et al.Modeling of load demand due to EV battery charging in distribution systems[J].IEEE Transaction on Power System，2011，26(2)：802-810.

[13]Staats P T，Grady W M，Arapostathis A，et al.A statistical analysis of the effect of electric vehicle battery charging on distribution system harmonic voltages[J].IEEE Transactions on Power Delivery，1998，13(2)：640-646.

[14]Taylor M J，Alexander A.Evaluation of the impact of plug-in electric vehicle loading on distribution system operations[C].IEEE Power & Energy Society General Meeting，Calgary，Canada，2009：1-6.

[15]Department for Transport.Transport Statistics Bulletin-National Travel Survey：2008[R].London：Department for Transport，2009.

[16]Zhang Peng，Qian Kejun，Zhou Chengke，et al.A methodology for optimization of power systems demand due to electric vehicle charging load[J].IEEE Transactions on Power System，2012，27(3)：1628-1636.

[17]刘次华，万建平.概率论与数理统计[M].北京：高等教育出版社，1999.

[18]Xu Hao，Miao Shihong，Zhang Chunyong，et al.Optimal placement of charging facilities for large-scale electric vehicles[J].International Journal of Electrical Power & Energy System，2013，53：159-165.

[19]田立亭，史双龙，贾卓.电动汽车充电功率需求的统计学建模方法[J].电网技术，2010，34(11)：126-130. Tian Liting，Shi Shuanglong，Jia Zhuo.A statistical model for charging power demand of electric vehicles[J].Power System Technology，2010，34(11)：126-130.

[20]Shahidinejad S，Filizadeh S，Bibeau E.Profile of charging load on the grid due to plug-in vehicles[J].IEEE Transactions on Smart Grid，2012，3(1)：135-141.

A Modeling Strategy for Charging Loads of Large-Scale Electric Vehicles Considering Multi-days Spaced Charging Mode

XuHaoMiaoShihongQianTiantianRanXiaohong

(State Key Laboratory of Advanced Electromagnetic Engineering and Technology Huazhong University of Science and Technology Wuhan 430074 China)

This paper presents a modeling strategy for charging loads of large-scale electric vehicles considering multi-days spaced charging mode，which can provide necessary theoretical bases for charging load forecasting and ordered charging control method.Six user sets are firstly suggested according to the daily travel distance.Then，on the basis of a detailed analysis on the probability characteristics of the charging starting time and the charging duration of a single electric vehicle from each user set，a calculation method for the load expectation of a single user set at specified time instant is proposed.After that，the concept of the initial date window is put forward，and the probability distributions of the uses with two kinds of multi-days spaced charging modes in the initial date window are simulated respectively.Finally，based on the law of large numbers，the overall load calculation model and its discrete approach for the aggregated charging load on each workday are proposed.According to the result of example analysis，the strategy can significantly im-prove the battery capacity utilization of large-scale electric vehicles，achieve more accurate charging load characteristics with a good maneuverability，and thus would have consider able application prospects.

Electric vehicle，multi-days spaced charging，load modeling，probability characteristics，the law of large numbers，discreteapproach

国家高技术研究发展计划(“863”计划)(2011AA05A109)资助项目。

2014-12-07 改稿日期2015-02-05

TM73

徐 浩 男，1987年生，博士研究生，研究方向为电力系统继电保护、配电网新技术。

苗世洪 男，1963年生，教授，博士生导师，研究方向为电力系统继电保护、变电站综合自动化、微网及配电网新技术等。(通信作者)