基于小波变换的风电场短期风速组合预测

田中大 李树江 王艳红 高宪文

(1.沈阳工业大学信息科学与工程学院 沈阳 110870 2.东北大学信息科学与工程学院 沈阳 110819)



基于小波变换的风电场短期风速组合预测

田中大1李树江1王艳红1高宪文2

(1.沈阳工业大学信息科学与工程学院 沈阳 110870 2.东北大学信息科学与工程学院 沈阳 110819)

针对风电场短期风速的预测提出一种基于小波变换的组合预测方法。首先利用Mallat算法对短期风速时间序列进行db3小波三层分解与重构，得到短期风速时间序列的近似分量和细节分量。针对近似分量和细节分量的不同特性，对近似分量利用粒子群算法优化的最小二乘支持向量机进行预测，对细节分量利用自回归求和滑动平均模型进行预测。最后各预测模型预测值组合叠加得到最终的短期风速预测值。仿真结果表明该方法具有较高的预测准确度。

短期风速 小波变换 自回归求和滑动平均模型 最小二乘支持向量机 组合预测

0 引言

随着化石燃料的日益枯竭及环境污染的日益严重，风能作为一种无污染的可再生能源，得到世界各国的高度重视，风力发电成为世界各国重点发展的可再生能源发电技术之一[1]。但研究发现风速的随机性导致风电并网后对电力系统的稳定性产生严重影响[2]。目前解决这一问题的方法有两种，一是增加风电装机容量与常规机组的旋转备用容量，以抑制风电并网对电网带来的冲击，但这会增加系统的运行费用；二是对风速或风电功率做出较准确的预测，以及时对电网进行调度，提高风力发电的经济性。风速预测分为长期、中期和短期预测，其中以“h”为预测单位的短期风速预测一般是提前1～48 h对未来以h为单位的风速进行预测，有效的短期风速预测对风力发电行业具有重要的应用价值[3，4]。

目前，风速预测方法可分为基于物理模型和历史数据两大类。基于物理模型的预测方法一般采用数值天气预报(Numerical Weather Prediction，NWP)数据[5，6]，但在我国，很难获得数值天气预报模型，因此，目前基于历史数据的风速预测研究具有广阔的应用前景。

国内外学者利用基于历史数据的预测方法对短期风速预测问题进行了广泛研究，主要包括传统的时间序列模型与人工智能预测模型。时间序列模型中的自回归滑动平均(Auto Regressive Moving Average，ARMA)模型[7]、差分自回归滑动平均(Auto Regressive Integrated Moving Average，ARIMA)模型[8，9]在短期风速预测中得到了大量应用。但文献[10，11]中相关研究表明，短期风速是典型的非线性的时间序列，而基于自回归的ARMA、ARIMA等模型理论上是适合线性时间序列的预测，对于具有非线性特点的短期风速时间序列应用偏少。虽然时间序列模型中也包含随机波动模型[12]、TAR[13]、STAR[14]等非线性模型，但在短期风速预测中的应用很少见于文献之中。近些年出现的人工智能预测模型使得短期风速的预测进入了一个新的高度，包括支持向量机(Support Vector Machine，SVM)[15，16]、最小二乘支持向量机(Least Square Support Vector Machine，LSSVM)[17，18]、卡尔曼滤波[19]以及人工神经网络[20，21]等模型。虽然人工智能预测模型较时间序列模型在预测准确度上有一定提高，但也存在各自的问题。SVM与LSSVM预测模型虽然需要的样本数少，但其关键参数很难确定。卡尔曼滤波器则要求精确已知系统的数学模型与噪声统计特性，否则其性能将发散。而人工神经网络存在易陷于局部最优值、网络结构难以确定的问题。

J.M.Bates等[22]首先提出了经济科学领域的组合预测思想，即通过一组模型进行预测，通过组合预测模型的结果取加权平均以改进预测效果[23]。虽然组合预测模型也存在如何进行预测模型的选取以及权重分配问题，但也可作为短期风速预测的一个发展方向，本文尝试利用组合预测模型进行短期风速预测的研究。组合预测模型就是把不同的预测模型综合起来，取长补短，从而达到提高预测准确度和增加预测可靠性的效果。因此，本文利用小波变换对原始短期风速时间序列进行分解与重构，得到短期风速序列的近似分量和细节分量，利用Hurst参数进行分析，可知近似分量具有长相关非线性的特性，适合利用对非线性时间序列具有良好预测效果的LSSVM进行预测，通过粒子群优化算法(Particle Swarm Optimization，PSO)进行LSSVM预测模型参数的优化。而细节分量具有短相关非平稳的特性，适合利用ARIMA模型进行预测，各分量的预测值经过最后的合成得到实际的预测值。由于对各分量分别采用单独的合适模型进行预测，因此本文方法具有较高的预测准确度。最后短期风速的多步预测仿真验证了本文方法的有效性。

1 基于小波变换的短期风速时间序列分析

小波变换是采用正交基对信号进行分解[24]，离散小波变换由一系列参数组成。

cj(k)=〈X,φjk(t)〉
dj(k)=〈X,ψjk(t)〉

(1)

式中，〈*,*〉为内积运算；cj(k)为近似分量；dj(k)为细节分量；j,k∈Z； 尺度函数φjk(t)由母小波φ(t)通过平移预算与伸缩后得到

φjk(t)=2-j/2φ(2-jt-k)

(2)

φj(t)是一低通滤波器，可分离出输入信号中的低频成分，小波变换可将信号分解为大时间尺度的近似分量与不同小尺度下的细节分量的集合。

本文利用快速离散正交小波变换Mallat算法[25]进行给定短期风速序列的分解与重构。

将aj看作待分解的序列，根据分解算法有

aj+1=Haj，dj+1=Gdj，j=0,1,2,…,N

(3)

式中，H和G分别为低通滤波器和高通滤波器，Mallat算法将原短期风速序列分解为低频的近似分量以及高频的细节分量。 近似分量可反映短期风速的变化趋势和特征，而细节分量则反映扰动等动态因素。

分解后的短期风速序列可由Mallat算法进行重构，算法为

aj-1=ajH*+djG*

(4)

式中，H*与G*分别为H和G的对偶算子；j=0,1,2,…,N。Mallat重构算法利用二插值，即在输入序列每相邻序列之间补零，保持分解重构序列长度的一致。

Daubechines小波对于非平稳时间序列具有很好的特性，但是不同N值的dbN小波得到不同的处理效果，N越大计算时间越长，本文参考文献[24]并通过实验决定采用db3小波。而分解层数主要和信噪比有关，当信噪比较低时，输入信号主要以噪声为主，这时分解层数应选择大一点，有利于信噪分离；而当信噪比较高时，主要以信号为主，这时分解层数不必太大，否则重构时失真较严重，误差也大。综合考虑，本文采用三次分解与重构来保证实时性与预测准确度。

采集东北某电厂测得的2013年3月1日0∶00到2013年3月13日12∶00，采样间隔1 h的300组短期风速数据。对该300组短期风速时间序列进行db3小波分解，图1给出了短期风速原始数据、分解重构后近似分量Ca3与细节分量Cd1、Cd2、Cd3的波形图。

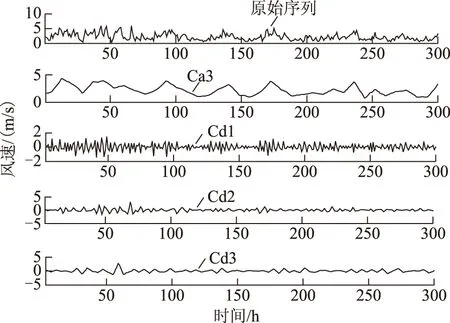
图1 短期风速序列的db3分解Fig.1 db3 decompose of short-term wind speed time series

从图1中可看出，近似分量与短期风速的实际变化趋势接近，而细节分量随着分解阶数的增加，其序列变得逐渐平滑。对于小波分解后的近似分量与细节分量选择合适的预测模型是非常重要的，本文利用时间序列的Hurst参数选择合适的模型。Hurst参数H可用来衡量时间序列的相似性，当H=0.5时说明时间序列是随机游走的，事件之间不相关，当H∈[0,0.5)时说明序列是反持久性的，当H∈(0.5,1)时说明序列是持久性的，也即具有自相似性，H越大则序列的自相似性越大。因此Hurst参数越大说明时间序列的自相似(长相关)程度越高[26]。利用R/S类方法[27]进行Hurst参数的计算，结果如表1所示。

表1 各分量的Hurst参数Tab.1 The Hurst parameter of components

由表1可知，近似分量的Hurst参数与原始风速序列相近，反映了近似分量具有长相关以及强非线性的特点，因此对其采用对非线性序列具有良好预测效果的LSSVM进行建模与预测。3个细节分量具有较小的Hurst参数，反映了原始流量序列的随机波动特性，呈现一种周期非平稳的特征，而ARIMA模型对周期非平稳数据序列能够有效地分析其数据序列相关性，所以本文采用了ARIMA模型对低频细节分量进行建模与预测。

2 ARIMA模型

ARIMA模型是Box与Jenkins提出的时间序列预测方法，是差分运算与ARMA模型的结合。任何非平稳序列实现差分后平稳，即可对该序列进行ARIMA建模。ARIMA模型可表示为

(5)

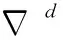
(6)

自回归算子φ(B)为p阶，滑动平均算子θ(B)为q阶，且通过d阶差分，则此过程可写成ARIMA(p，d，q)模型，d为差分阶数，p为自回归阶数，q为滑动平均阶数。因此ARIMA模型基本思想是对非平稳序列用若干次差分使其成为平稳序列，差分次数是参数d，再用以p、q为参数的ARMA模型对该平稳序列建模，之后经过反变换得到原序列。

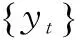
自协方差

(7)

自相关函数

(8)

偏相关函数为

(9)

可通过ρk、αk的截尾性确定模型的阶数。有如下3种情况[28]：

1)若ACF在q步截尾，则可判定p=0，模型为MA(q)。

2)若PACF在q步截尾，则可判定q=0，模型为AR(p)。

3)若ACF与PACF均拖尾，则可判定模型为ARMA(p，q)。

当确定了模型参数后，即可按式(10)进行时间序列的预测。

yt=θ0+φ1yt-1+…+φpyt-p+εt-θ1εt-1-…-θqεt-q

(10)

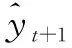
3 PSO优化的LSSVM预测模型

最小二乘支持向量机是通过一个非线性映射φ， 把样本空间映射到一个高维乃至无穷维的特征空间中，在此特征空间中y(x)=wφ(x)+b， 使得在原来的样本空间中非线性问题转化为在特征空间中的线性问题。其中w为权系数向量，b为常值偏差。最优的w和b可通过最小化的目标函数得到。

(11)

建立拉格朗日函数求解上述的约束优化问题

(12)

式中，ak为拉格朗日乘子，对该拉格朗日函数求极值，上述优化问题转换为对以下线性方程组的求解

(13)

对于非线性时间序列回归问题，一般选择径向基函数作为核函数。即

(14)

式中，σ2为径向基的核函数宽度。

假设k时刻的某时间序列为x(k)， 将输入时间序列转化为矩阵形式

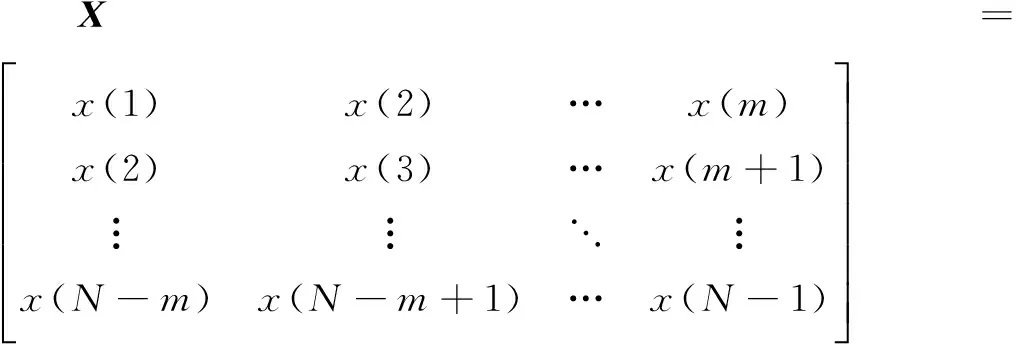
(15)

式中，N为输入时间序列的总长度；m为嵌入维数。令p为预测步数，则输出的预测矩阵Y可表示为

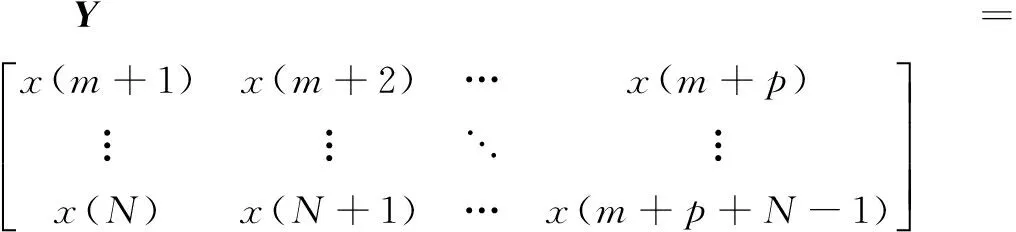
(16)

将时间序列样本数据按照式(15)生成输入矩阵，按照式(16)生成输出矩阵，即可完成LSSVM预测模型的建模训练[29]。

LSSVM的预测效果与正则化参数γ、径向基的核函数宽度σ2以及嵌入维数m的选择有很大关系，因此，如何合理选择这些参数十分重要。本文选取PSO算法进行LSSVM预测模型参数的优化[30]。其寻优步骤可描述如下：

步骤1：初始化粒子群算法的参数，包括：惯性权重、学习因子、群体规模、最大迭代次数等。

步骤2：分别使用每个粒子所对应的LSSVM对训练样本进行预测，将预测值与实际值的均方根误差作为各粒子的适应度值，再将每个粒子的当前适应度值与该粒子自身的最优适应度值进行比较。如果当前粒子更优，则选择粒子当前的位置作为该粒子的最优位置。

步骤3：将各粒子自身最优位置适应度值与群体的最优位置适应度值进行比较，如果该粒子更优，则将该粒子的最优位置作为群体的最优位置。

步骤4：按照PSO算法更新粒子的速度和位置。

步骤5：检查是否满足寻优结束的条件(达到预先设定的最大迭代次数或预先设定的精度)。若满足，则寻优结束，求出最优解；否则转至步骤2，继续新一轮搜索。

4 基于小波的短期风速组合预测模型

本文的短期风速组合多步预测方法可表示成图2所示，其中小波算法采用db3小波进行三层分解与重构。

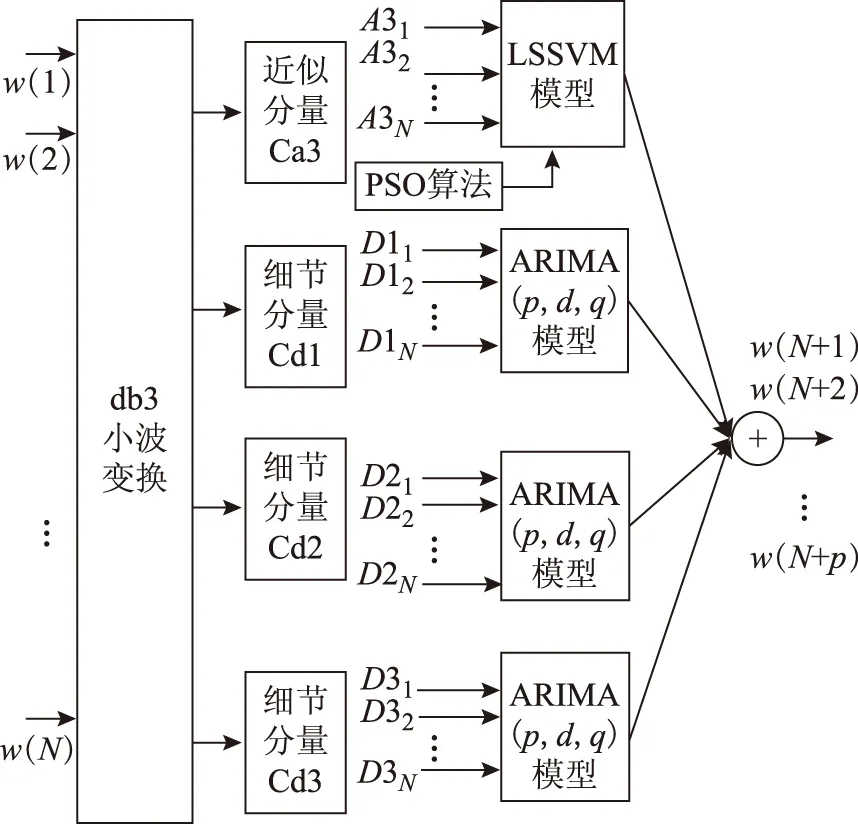
图2 基于小波的短期风速组合预测模型Fig.2 Combined prediction model based on wavelet transform

从图2可得出本文预测方法的步骤如下：

步骤1：对于长度为N的短期风速时间序列w(1),w(2),…,w(N)，将其进行db3小波三层分解重构，得到一个近似分量Ca3与3个细节分量Cd1、Cd2、Cd3，分量长度还为N，近似分量是长相关非线性时间序列，而细节分量是短相关非平稳的时间序列。

步骤2：将近似分量Ca3采用LSSVM进行训练建模，同时利用PSO算法对LSSVM预测模型参数进行优化。

步骤3：对3个细节分量Cd1、Cd2、Cd3采用ARIMA模型进行训练，通过ACF与PACF确定3个模型的参数p、d、q。

步骤4：LSSVM与ARIMA模型建立完毕之后，对测试样本短期风速序列按步骤1进行分解与重构，进入训练完成的模型分别进行未来p步短期风速预测。将4路预测输出预测值进行组合相加加得到最终的短期风速预测值。

5 仿真

利用上文的300组短期风速数据，前276组数据用于模型建模，后24组一天24 h的风速作为测试集验证预测模型的预测准确度。

5.1 样本数据的预处理

在短期风速序列样本数据的采集过程中，可能会受传感器故障、人为原因、环境因素及其他异常情况的影响，存在一些异常不能反映风速真实情况的数据，如果利用这些数据进行预测模型的建立将会影响建模的准确度，因此需要将这些离群点数据进行剔除。本文采用拉伊达准则去除不合理的数据，对于输入风速数据计算样本的平均值

(17)

然后计算样本序列的标准差

(18)

对于样本序列，满足式(19)则认为是合理的。

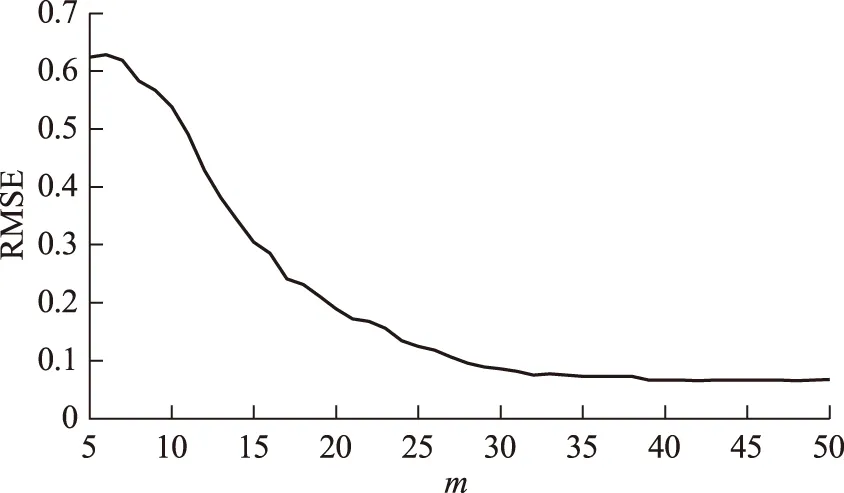
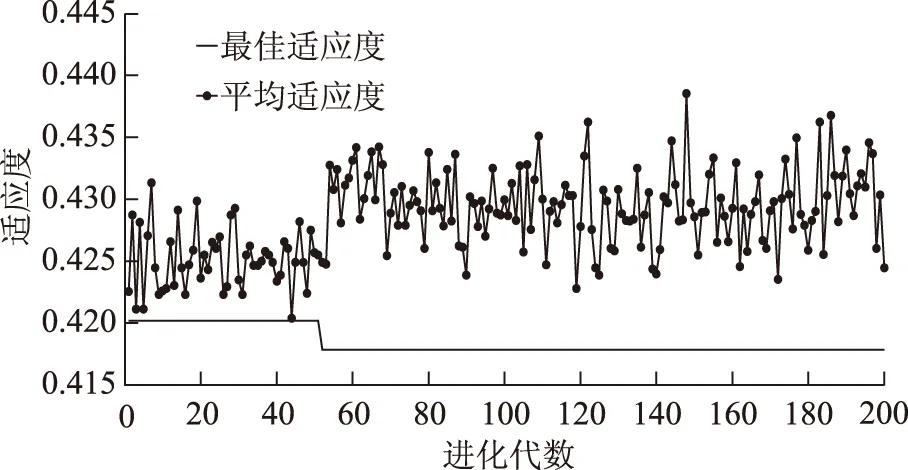
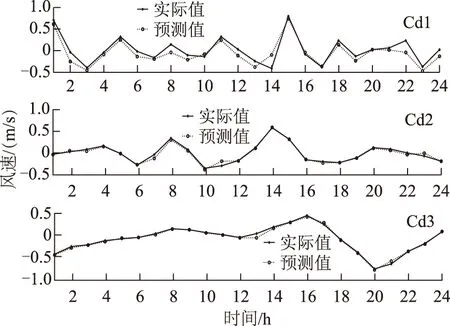
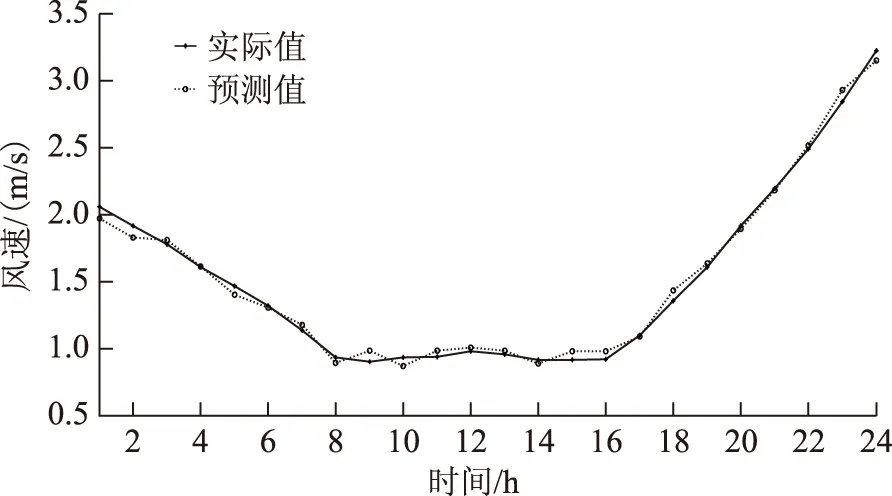
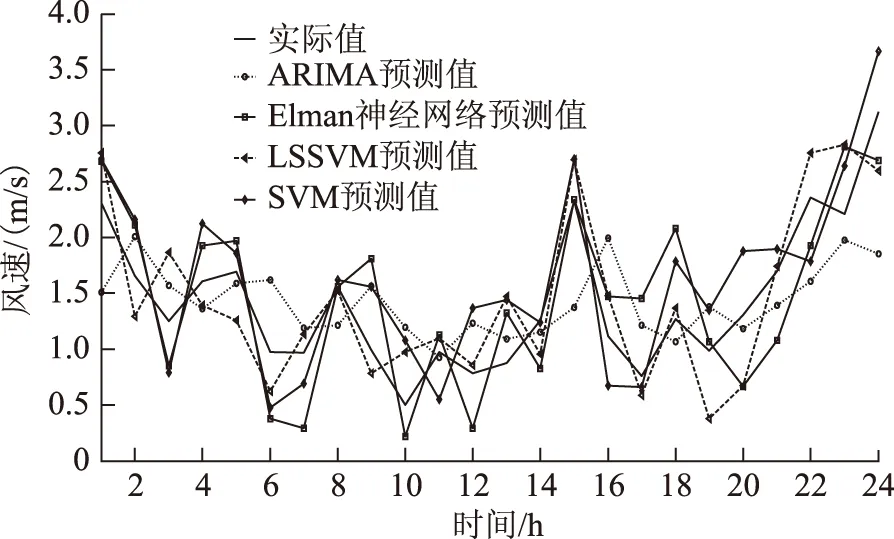
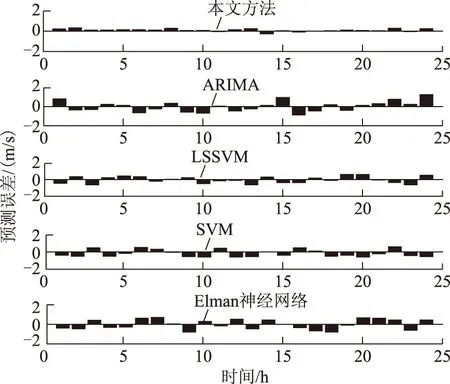
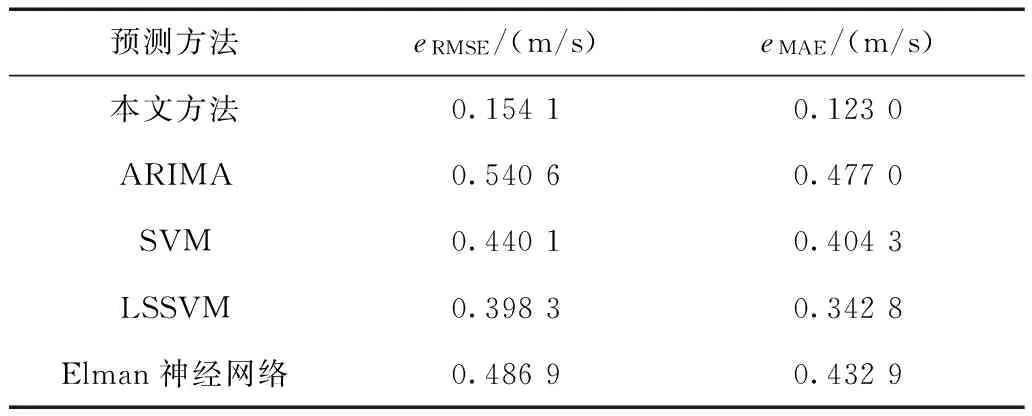
μ-3σ

(19)

式中，yi为输入样本；μ为样本均值；σ为标准差。

不符合该式(19)的训练数据认为是不合理数据，予以剔除，然后采用一维插值的方法补充数据。

5.2 模型参数确定

对短期风速序列的3个近似分量按照第2节描述进行ARIMA预测模型的建立，模型合理性检测通过AIC(赤池信息量准则)判定，建模完毕后其模型参数以及对应的AIC如表2所示。

表2 细节分量模型参数Tab.2 The parameter of detail components

(20)

将嵌入维数m设为10，图3为γ∈[1,100]，σ2∈[1,100]， 增长步长都为1时RMSE的变化图。将γ与σ2都设为10，图4为m∈[5,50]， 增长步长为1时RMSE的变化图。从图3与图4可看出3个参数对于LSSVM的预测效果有很大影响。如何选择最佳的预测参数是个重要问题。本文利用PSO算法来进行最优参数的选取。

图3 不同γ与σ2对预测效果的影响Fig.3 Different γ and σ2 on the effects of prediction

图4 不同m对预测效果的影响Fig.4 Different m on the effects of prediction

将待优化参数γ、σ2、m看作PSO算法的粒子进行迭代寻优。PSO优化算法的参数为：种群数T=30，最大的迭代次数G=200，学习因子c1=1.5，c2=1.7，惯性权重为1，待优化参数取值范围为γ∈[0.01,1 000]，σ2∈[0.01,1 000]，m∈[5,50]。 图5给出了预测步长p=24时，近似分量预测模型进行优化所对应的PSO算法适应度收敛曲线，优化之后得到的参数为：γ=1.375，σ2=155.06，m=36。

图5 适应度曲线Fig.5 The fitness curve

5.3 预测仿真

在得到细节分量的ARIMA预测模型与近似分量的LSSVM预测模型的参数之后，对24组短期风速测试数据进行了预测，图6为3个细节分量的预测结果，图7为近似分量的预测结果。将细节分量与近似分量的预测值进行组合相加即可得到最终的预测值，图8为本文方法最后的预测值与实际值的对比曲线。

图6 细节分量预测对比曲线Fig.6 The compared curve of detail components

图7 近似分量预测对比曲线Fig.7 The compared curve of approximation component

图8 本文方法最终预测对比曲线Fig.8 The compared curve of method in this paper

为了衡量本文方法预测准确度的提高，与ARIMA[8](预测模型参数为p=3，d=0，q=2)、SVM[16](网格法交叉验证得到参数为c=4.61，g=4.82)、LSSVM[17](网格法交叉验证得到参数为γ=3.84，σ2=10.85)和Elman神经网络[21](输入层为40，中间层为30，输出层为24，最大迭代次数为5 000)进行了预测效果与准确度的对比。图9给出了这几种预测方法短期风速预测值与实际值的对比曲线。从图8与图9对比可知，本文的组合预测方法在风速预测曲线拟合度上要好于其他几种方法，能够较好地拟合短期风速序列的变化趋势。

图9 其他预测方法预测对比曲线Fig.9 The compared curve of other methods

图10给出了本文组合预测方法与其他几种方法的误差分布图。从图中可观察到，本文的组合预测方法具有更小的预测误差，同时预测误差分布更加均匀化，即预测误差随着预测步长的变化幅度不大，而其他几种预测方法的预测误差对于不同的预测步长存在较大的差异，因此本文的组合预测方法具有更好的预测效果。

图10 预测误差分布图Fig.10 The distribution curve of predicted error

为了进一步说明本文预测方法预测准确度的提高，表3为文中几种预测方法风速预测值与实际值误差的RMSE，以及平均绝对误差(MAE)的对比，其中，MAE也是衡量预测准确度的指标，其定义为

(21)

表3 几种预测方法预测指标对比Tab.3 The comparison of several predictive methods

从表3的预测指标可知本文的组合预测方法的预测指标都优于其他常见的预测方法，其预测准确度的提高在于对短期风速时间序列通过小波分解重构，得到近似分量与细节分量，针对近似分量与细节分量的不同特性采用合适的预测模型进行预测。

6 结论

1)针对短期风速的多步预测问题而提出一种基于小波的组合预测方法。利用db3小波对原始风速序列进行分解重构，得到近似分量与细节分量。利用时间序列的Hurst参数对近似分量与细节分量进行分析。近似分量具有长相关非线性的特征，因此采用LSSVM对近似分量进行预测，并且利用PSO算法对LSSVM预测模型参数进行优化。细节分量具有短相关非平稳的特征，因此利用ARIMA模型进行预测。近似分量与细节分量的预测值经过组合叠加得到最终的短期风速预测值。通过实际采集的风速数据进行了预测效果的仿真，仿真结果表明本文的预测方法具有更高的预测准确度与更好的预测效果。

2)由于短期风速是不断变化的，而模型参数是通过一定数量数据样本训练生成的，随着时间的推移，预测模型的参数可能无法适应新的风速序列。针对该问题，本文在实际应用中拟采取一种离线与在线训练相结合的方法，即预测系统对预测误差进行累计，并设置一阈值，当累计的预测误差和大于该阈值时，重新启动模型的训练过程，生成新的模型参数来适应短期风速时间序列特性的变化，本文将在未来展开该方面的研究工作。

[1] 修春波，刘新婷，张欣，等.基于混沌特性分析的风速序列混合预测方法[J].电力系统保护与控制，2013，41(1)：14-20. Xiu Chunbo，Liu Xinting，Zhang Xin，et al.Hybrid prediction method of wind speed based on chaotic characteristic[J].Power System Protection and Control，2013，41(1)：14-20.

[2] 杨锡运，孙宝君，张新房，等.基于相似数据的支持向量机短期风速预测仿真研究[J].中国电机工程学报，2012，32(4)：35-41. Yang Xiyun，Sun Baojun，Zhang Xinfang，et al.Short-term wind speed forecasting based on support vector machine with similar data[J].Proceedings of the CSEE，2012，32(4)：35-41.

[3] Bouzgou H，Benoudjit N.Multiple architecture system for wind speed prediction[J].Applied Energy，2011，88(7)：2463-2471.

[4] Ma Lei，Luan Shiyan，Jiang Chuanwen，et al.A review on the forecasting of wind speed and generated power[J].Renewable and Sustainable Energy Reviews，2009，13(4)：915-920.

[5] Pelikan E，Eben K，Resler J，et al.Wind power forecasting by an empirical model using NWP outputs[C].2010 9th International Conference on Environment and Electrical Engineering，Prague，Czech，2010：45-48.

[6] Cuo Lan，Zhang Yongxin，Wang Qingchun，et al.Climate change on the northern Tibetan Plateau during 1957-2009：spatial patterns and possible mechanisms[J].Journal of Climate，2013，26(1)：85-109.

[7] Erdem E，Shi J.ARMA based approaches for forecasting the tuple of wind speed and direction[J].Applied Energy，2011，88(4)：1405-1414.

[8] 蒋金良，林广明.基于ARIMA模型的自动站风速预测[J].控制理论与应用，2008，25(2)：374-376. Jiang Jinliang，Lin Guangming.Automatic station wind speed forecasting based on ARIMA model[J].Control Theory & Applications，2008，25(2)：374-376.

[9] Liu Hui，Tian Hongqi，Li Yanfei.Comparison of two new ARIMA-ANN and ARIMA-Kalman hybrid methods for wind speed prediction[J].Applied Energy，2012，98：415-424.

[10]Xiao Hongfei，Ding Tao.Chaotic prediction method of short-term wind speed[C].Proceedings of the 2011 International Conference on Informatics，Cybernetics，and Computer Engineering，Melbourne，Australia，2012，112：479-487.

[11]Soman S S，Zareipour H，Malik O，et al.A review of wind power and wind speed forecasting methods with different time horizons[C].North American Power Symposium(NAPS)，2010，Arlington，TX，2010：1-8.

[12]李汉东，张世英.随机波动模型的持续性和协同持续性研究[J].系统工程学报，2002，17(4)：289-295. Li Handong，Zhang Shiying.Research on volatility persistence and co-persistence in stochastic volatility model[J].Journal of Systems Engineering，2002，17(4)：289-295.

[13]吴武清，李东，潘松，等.三阶段均值回复、TAR及其应用[J].系统工程理论与实践，2013，33(4)：901-909. Wu Wuqing，Li Dong，Pan Song，et al.Three-regime mean reversion、TAR and its application[J].System Engineering-Theory & Practice，2013，33(4)：901-909.

[14]Teräsvirta T.Specification，estimation，and evaluation of smooth transition autoregressive models[J].Journal of the american Statistical association，1994，89(425)：208-218.

[15]陈妮亚，钱政，孟晓风，等.基于空间相关法的风电场风速多步预测模型[J].电工技术学报，2013，28(5)：15-21. Chen Niya，Qian Zheng，Meng Xiaofeng，et al.Multi-step ahead wind speed forecasting model based on spatial correlation and support vector machine[J].Transactions of China Electrotechnical Society，2013，28(5)：15-21.

[16]Wang Y，Wu D L，Guo C X，et al.Short-term wind speed prediction using support vector regression[C].IEEE Power and Energy Society General Meeting，Minneapolis，MN，2010：1-6.

[17]Li X，Wang X，Zheng Y H，et al.Short-term wind power forecasting based on least-square support vector machine (LSSVM)[J].Applied Mechanics and Materials，2014，448-453：1825-1828.

[18]曾杰，张华.基于蚁群优化的最小二乘支持向量机风速预测模型研究[J].太阳能学报，2011，32(3)：296-300. Zeng Jie，Zhang Hua.Wind speed forecasting model study based on least squares support vector machine and ant colony optimization[J].Acta Energiae Solaris Sinica，2011，32(3)：296-300.

[19]Louka P，Galanis G，Siebert N，et al.Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering[J].Journal of Wind Engineering and Industrial Aerodynamics，2008，96(12)：2348-2362.

[20]刘进宝，丁涛.基于径向基函数神经网络的风速预测[J].太阳能学报，2012，33(7)：1131-1135. Liu Jinbao，Ding Tao.Wind speed prediction model based on radial basis functional neural network[J].Acta Energiae Solaris Sinica，2012，33(7)：1131-1135.

[21]Fourati F，Chtourou M.A greenhouse control with feed-forward and recurrent neural networks[J].Simulation Modelling Practice and Theory，2007，15(8)：1016-1028.

[22]Bates J M，Granger C W J.The combination of forecasts[J].Operations Research Quarterly，1969，20(4)：415-468.

[23]Granger C W J.Some thoughts on the development of cointegration[J].Journal of Econometrics，2010，158(1)：3-6.

[24]魏永涛，汪晋宽，王翠荣，等.基于小波变换与组合模型的网络流量预测算法[J].东北大学学报(自然科学版)，2011，32(10)：1382-1385. Wei Yongtao，Wang Jinkuan，Wang Cuirong，et al.Network traffic prediction algorithm based on wavelet transform and combined model[J].Journal of Northeastern University，2011，32(10)：1382-1385.

[25]Mallat S.A Wavelet Tour of Signal Processing[M].2nd ed.New York：Academic Press，1999.

[26]Qian B，Rasheed K.Hurst exponent and financial market predictability[C].Proceedings of The 2nd IASTED international conference on financial engineering and applications，Cambridge，MA，2004：203-209.

[27]田中大，高宪文，李琨.基于EMD与LS-SVM的网络控制系统时延预测方法[J].电子学报，2014，42(2)：868-874. Tian Zhongda，Gao Xianwen，Li Kun.Time-delay prediction method of networked control system based on EMD and LS-SVM[J].Acta Electronica Sinica，2014，42(2)：868-874.

[28]王振雷，唐苦，王昕.一种基于D-S和ARIMA的多模型软测量方法[J].控制与决策，2014，29(7)：1160-1166. Wang Zhenlei，Tang Ku，Wang Xin.A multi-model soft sensing method based on D-S and ARIMA model[J].Control and Decision，2014，29(7)：1160-1166.

[29]田中大，高宪文，石彤.用于混沌时间序列预测的组合核函数最小二乘支持向量机[J].物理学报，2014，63(16)：160501-160508. Tian Zhongda，Gao Xianwen，Shi Tong.Combination kernel function least squares support vector machine for chaotic time series prediction[J].Acta Physica Sinica，2014，63(16)：160501-160508.

[30]田中大，高宪文，李琨.基于预测控制的NCS时延补偿算法[J].系统工程与电子技术，2013，35(10)：2165-2169. Tian Zhongda，Gao Xianwen，Li Kun.Networked control system time-delay compensation algorithm based on predictive control[J].System Engineering and Electronics，2013，35(10)：2165-2169.

Short-Term Wind Speed Combined Prediction for Wind Farms Based on Wavelet Transform

TianZhongda1LiShujiang1WangYanhong1GaoXianwen2

(1.College of Information Science and Engineering Shenyang University of Technology Shenyang 110870 China 2.College of Information Science and Engineering Northeastern University Shenyang 110819 China)

In order to improve short-term wind speed prediction accuracy of wind farms，a combined prediction method based on the wavelet transform is proposed.Firstly，the db3 wavelet is used for three-layer decomposition and reconstruction for short-term wind speed time series through Mallat algorithm.The approximation components and the detail components of the short-term wind speed are then obtained.Next，according to the different characteristics of these components，the least square support vector machine optimized by particle swarm algorithm and the autoregressive integrated moving average model are adopted as the predictive models for the approximate components and the detail components respectively.Then，the final predictive value of the short-term wind speed is obtained by the combination of the two components.The simulation results indicate that higher accuracy can be obtained in this prediction method.

Short-term wind speed，wavelet transform，auto regressive integrated moving average，least square support vector machine，combined prediction

国家自然科学基金重点项目(61034005)和辽宁省博士科研启动基金(20141070)资助。

2014-12-04 改稿日期2015-02-02

TM614

田中大 男，1978年生，博士，讲师，研究方向为混沌时间序列预测、网络控制系统时延补偿与调度方法。(通信作者)

李树江 男，1966年生，博士，教授，研究方向为复杂工业过程建模与优化控制。