多相分数槽集中绕组表贴式永磁电机谐波电流的确定及其影响
康惠林 周理兵 王 晋 彭 溪
(强电磁场工程与新技术国家重点实验室(华中科技大学) 武汉 430074)
多相分数槽集中绕组表贴式永磁电机谐波电流的确定及其影响
康惠林 周理兵 王 晋 彭 溪
(强电磁场工程与新技术国家重点实验室(华中科技大学) 武汉 430074)
以一台20槽22极的五相分数槽集中绕组表贴式永磁电机为例进行分析。在保持电流有效值不变的前提下,以获得最大平均转矩为目标,采用解析法确定谐波电流分量,并通过有限元法得到验证。此外,对比分析电机在谐波电流注入前后电磁转矩、绕组磁动势、气隙磁密、涡流损耗、径向力波等性能的变化。分析表明,注入谐波电流后电机绕组磁动势出现新的谐波分量(包括低次分量),并导致涡流损耗和最低次径向力波含量增加。分析结果揭示了多相永磁电机设计的重点,为该类电机的设计提供参考。
多相永磁电机 谐波电流 电磁性能 影响
0 引言
多相电机转矩脉动小、控制灵活,被广泛用于船舶推进、多电飞机等领域[1,2]。分数槽集中绕组永磁电机效率高、相间互感小、容错性能好[3],得到了广泛研究和应用[4,5]。然而,该型电机最大的缺点在于磁动势谐波次数多,含量大,易引发不容忽视的永磁体涡流损耗、振动、噪声、铁心局部饱和等一系列问题[6,7]。因此,需要对该电机磁动势谐波的产生以及影响进行深入分析。文献[6]分析了分数槽集中绕组电机磁动势谐波与绕组结构的关系以及磁动势谐波对涡流损耗的影响。文献[8,9]指出多相分数槽集中绕组永磁电机定子磁动势、气隙磁密、转矩脉动及损耗受制于电机参数和驱动方式,并进一步分析了相数与供电方式、中性点接法、极槽匹配与绕组排布等对多相永磁电机的影响。
对于多相集中绕组电机,可通过注入谐波电流的方式优化气隙磁密分布和定子电流波形,以有效提高铁心利用率和功率密度[10-12]。然而,少有文献对谐波电流与基波电流的比例以及谐波电流对电机性能的影响进行全面分析。文献[10]根据转矩谐波系数确定电流角度和比例,文献[13]将多相电机等效为若干个虚拟三相电机进行控制分析,并给出电流比例关系。文献[14]研究引入三次电流的多相感应电机矢量控制问题,并分析电流角对铁心饱和与损耗提升的影响。文献[15]基于电机铜耗最小的原则分析了多相表贴式永磁电机在正常和故障状态下的最佳电流给定问题。
本文针对多相分数槽集中绕组表贴式永磁电机在注入谐波电流条件下的电机性能进行分析,并据此提出电机设计需要注意的问题。首先,以获得最大平均转矩为目标,并保持电机相电流在谐波电流注入前后有效值不变,得到谐波电流及其与基波分量的比例。提出采用二维解析法计算反电动势进而确定优化的电流,并通过有限元计算验证了解析结果。其次,对电机在谐波电流注入前后的转矩、绕组磁动势、气隙磁密、涡流损耗和径向力波等性能进行对比分析。其中,绕组磁动势的分析采用绕组函数法进行。最后,结合谐波电流对电机性能的影响,提出在多相分数槽集中绕组表贴式永磁电机设计时需要关注和解决的问题。
本文以一台五相20槽22极分数槽集中绕组表贴式永磁电机为例验证所采用的方法和结论。电机的横截面示意图如图1所示,图中表示出了绕组的排列顺序和连接方式。电机的主要设计参数见表1。
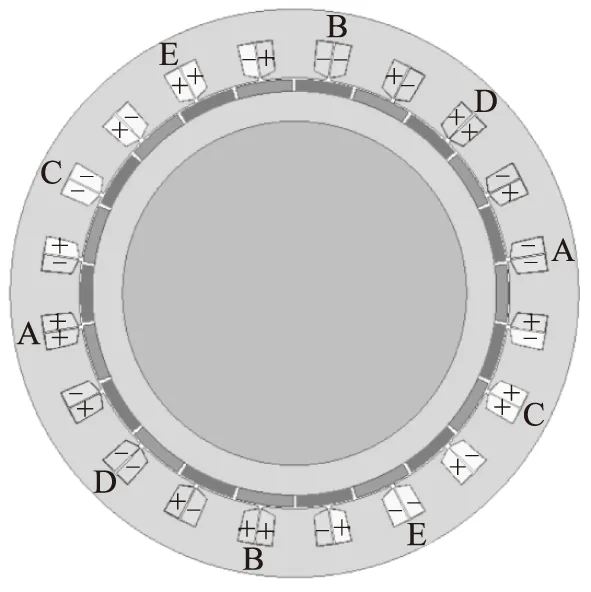
图1 五相20槽20极分数槽集中绕组永磁电机Fig.1 Five-phase 20-slot 22-pole fractional-slot concentrated winding permanent magnet machine
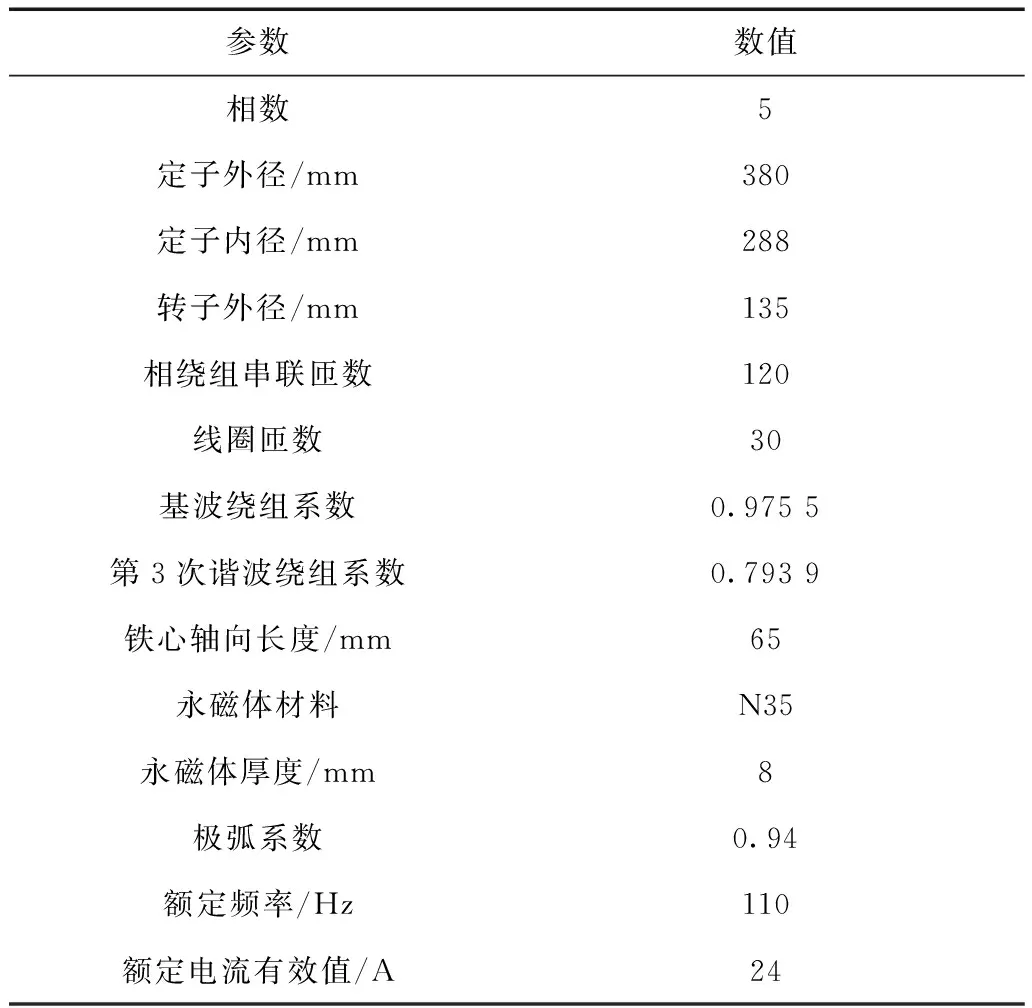
表1 样例电机主要设计参数Tab.1 Main design parameters of the sample machine
1 谐波电流的确定
利用次数小于相数的谐波电流提高多相电机转矩密度已得到充分的分析和验证[10-12]。但少有文献分析谐波电流含量与基波电流比例问题。
1.1 谐波电流的含量
谐波电流含量的确定原则可不尽相同。文献[10]保持谐波注入前后相电流幅值不变,基波电流幅值增大,有利于提高电机转矩,但增加了电机铜耗和绕组发热量,不利于电机长期运行。本文以获得最大平均转矩为目标,以保持相电流有效值不变为原则确定谐波电流,保证注入谐波电流前后铜耗不变。
对于m相集中绕组表贴式永磁电机,第i相反电动势可用傅里叶级数表示为
(1)
式中,Ek为第i相绕组反电动势的第k次谐波幅值;p为电机极对数;ωr为转子机械角速度。
如对第i相绕组注入电流,且采用最大转矩/电流的控制策略,则相电流可用傅里叶级数表示为
(2)
式中,Iv为第i相绕组反电动势的第v次谐波幅值。
保持相电流的有效值I0不变,则有
(3)
此时,电机的电磁转矩可表示为
(4)
式中
且n1为整数,n2是不为0的整数。
可见,当k=v时,第k次反电动势和第v次电流产生平均转矩。电机总平均电磁转矩可表示为
(5)
考虑到电流的约束条件(3),并利用拉普拉斯乘数法可得到平均电磁转矩最大时相电流第v次谐波幅值为
(6)
可见,为得到最大平均转矩,相电流各次谐波的比例与对应反电动势谐波比例相同。此时电机的平均电磁转矩可改写为
(7)
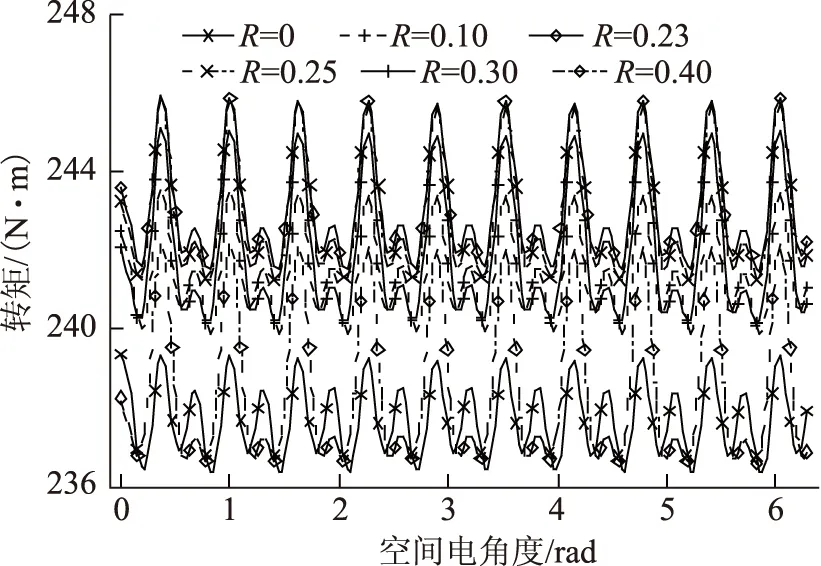
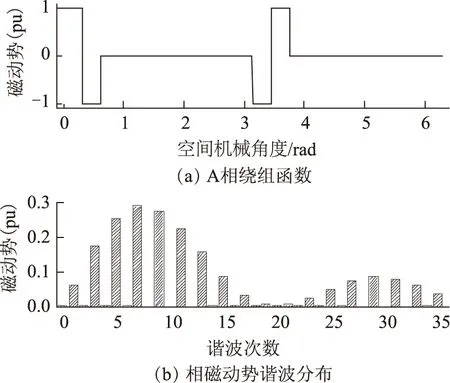
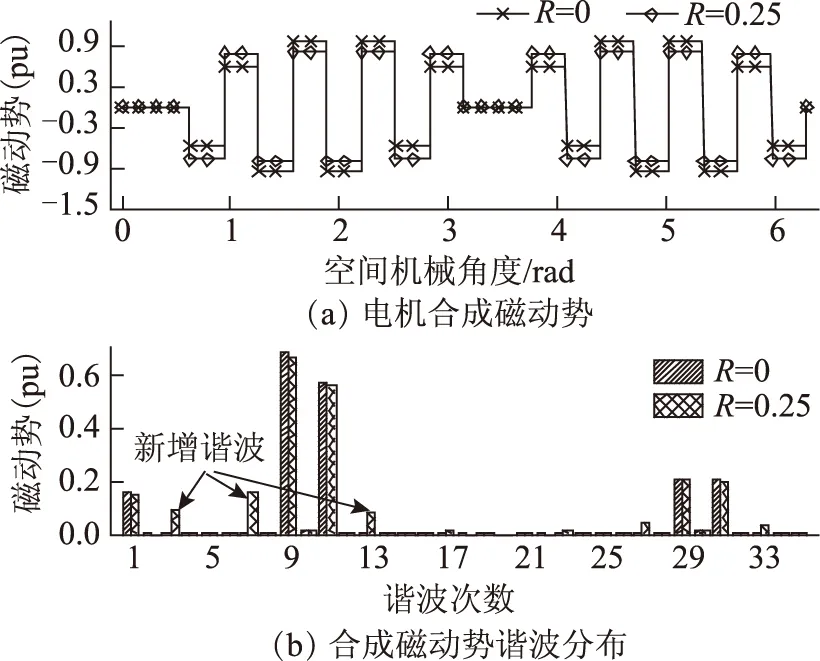
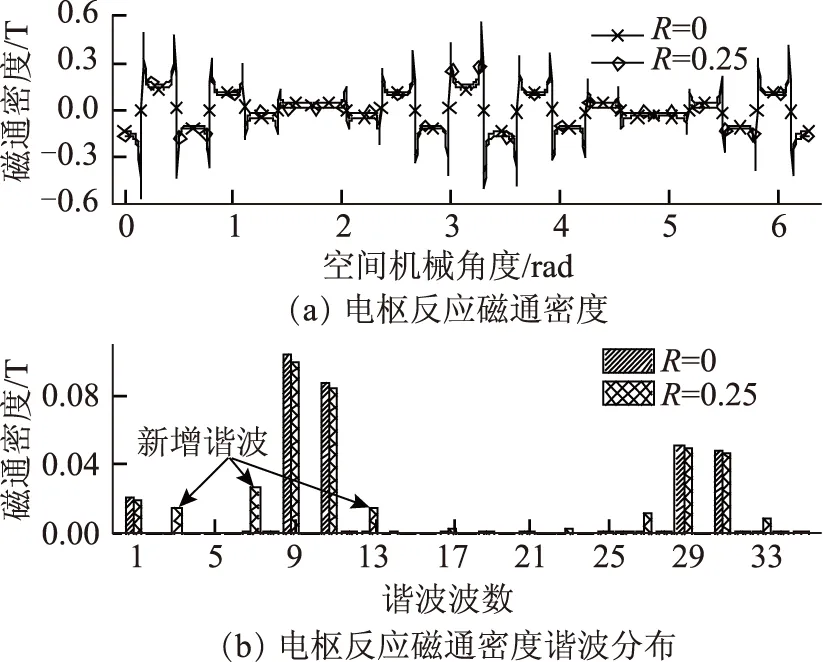
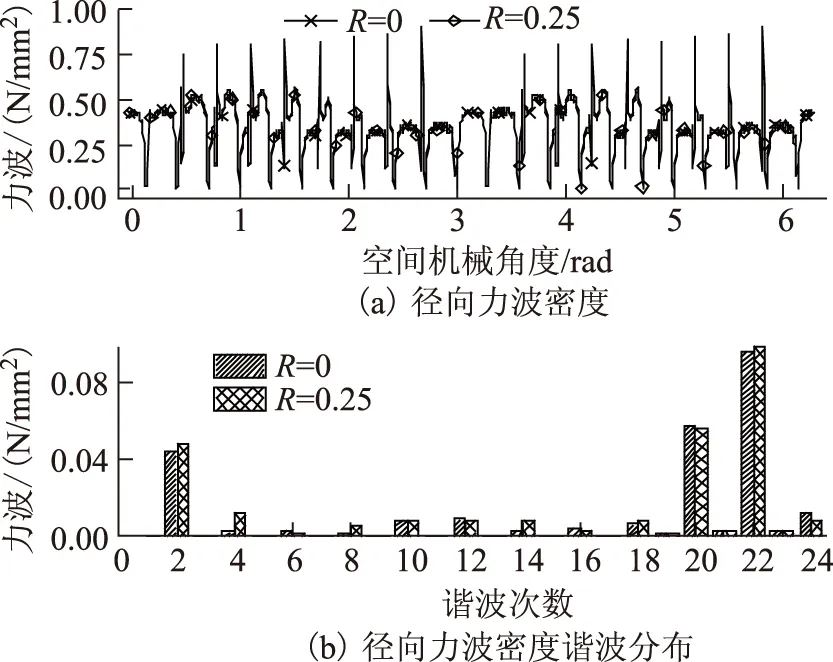
然而在实际电机控制场合,对高次电流谐波的定量控制难度大,付出的成本较高。折中办法是只考虑对特定次的电流谐波分量进行控制。对于m相表贴式集中绕组永磁电机而言,限定注入的谐波电流次数v (8) 而平均转矩可表示为 (9) 对比式(7)和式(9)可知,在只考虑次数低于相数的谐波电流时,电机的最大平均转矩将有所下降。但是,由于电机反电动势的高次谐波分量往往很小,两个最大平均转矩的值基本一致。因此,本文采用式(8)的电流分量。 1.2 谐波电流的解析计算 由前文可知,确定谐波电流含量时需得到反电动势及其谐波分布情况。一般而言,电机的反电动势可通过有限元计算得到,但需要完整的电机结构、材料参数。因此,该法对电机使用人员特别是只从事电机驱动的人员而言使用价值不高。此外,也通过测量的方式得到反电动势,但这可能受制于测量条件,对电机优化也无指导意义。二维解析法[16]物理概念清晰,根据电机定转子半径、气隙长度、绕组、永磁体材料和结构等数据即可计算电机反电动势,计算准确度高、速度快,适用于反电动势计算。 基于文献[16]的解析法,计算得到如图2所示的样例电机相反电动势。将该反电动势与采用有限元进行计算得到的结果进行对比。图2说明,采用解析法分析得到的电机反电动势与有限元计算结果较接近。其中,解析计算得到的1,3和5次分量分别是有限元结果的101.1%,109.7%和116.4%。计算值的差异主要是由于该解析法不考虑铁心饱和、开槽和漏磁等因素的影响。 图2 电机反电动势及其谐波Fig.2 The EMF and its harmonics of machine 根据解析结果,第3次谐波电流与基波电流幅值之比为0.25,而根据有限元结果,该比值则为0.23,两个比值的数值差异较接近。因此,可利用解析法确定谐波电流与基波电流的比例。 1.3 谐波电流的解析确定和有限元验证 本节采用有限元法验证样例电机谐波电流含量。定义R为相电流第3次谐波分量与基波分量幅值之比。保持相电流有效值为额定值,图3给出了R=0,0.10,0.23,0.25,0.30和0.40情况下的电机转矩,其中,R=0时电流只含基波分量。由图3可见,R=0.23时电机平均转矩值(243.1 N·m)最大,但与R=0.25时的值(242.8 N·m)差异极小。因此可见:①相电流各次谐波的比例与对应反电动势谐波比例相同时,电机获得最大转矩;②电机由解析法预测谐波电流和有限元法预测电流激励时,产生接近的转矩。因此,可通过解析法代替有限元法确定谐波电流。本文若不作特别说明,谐波电流R则等于0.25。 图3 电机转矩Fig.3 The torques of machine 图3给出了电机在谐波电流激励下的转矩。本节对谐波电流对转矩的影响进行分析。 式(9)所表示的电机平均电磁转矩可改写为 (10) 式中,α31、α(m-2)1分别为第3次、第m-2次反电动势谐波幅值与反电动势基波幅值之比。因此,电机在谐波电流与正弦电流驱动时的平均转矩之比为 (11) 例如,由图3可知R=0.25和R=0时样例电机的转矩(242.8 N·m和236.7 N·m)之比为1.026,而该电机解析计算得到的α31=0.225。可见,按照保持电流有效值不变原则,电机平均转矩的提升受限于电机反电动势谐波比例。因此,在电机设计时,应在保证反电动势基波较大的前提下,增大次数低于电机相数的反电动势谐波分量。比如,可优化槽极配合或绕组结构得到较大的基波和谐波绕组系数,进而提高相应的反电动势分量。 分析式(4),可将转矩脉动分量表示为 (12) 由式(12)可看出: 1)次数低于m的反电动势谐波不产生电磁转矩脉动分量。因此,确定这些反电动势的幅值及其与基波的比例时,只需要考虑对平均转矩的影响。 2)次数等于m的反电动势谐波也不产生电磁转矩脉动分量。另外,由式(9)可知,该反电动势谐波分量不参与平均转矩的产生。然而,在电机设计时,可保留该次谐波分量,从而使次数低于m的反电动势谐波幅值增大,进而提高平均转矩[17-19]。 3)次数大于m的反电动势谐波分量是产生转矩脉动的原因,其幅值应得到抑制。对于表贴式永磁电机,高次反电动势谐波分量可通过优化永磁体形状抑制气隙磁密以及反电动势的高次谐波分量[17-19]。 由于多相分数槽集中绕组电机相数和极数较大,转矩脉动分量的频率也较大,反电动势高次谐波分量幅值一般很小。因此,在分析转矩脉动幅值变化时可只考虑n2=1。此时电磁转矩脉动分量的频率在注入谐波电流前后保持不变,而幅值变化量为 (13) 由式(13)可见,注入谐波电流将造成电磁转矩脉动分量的变化。对于表贴式集中绕组永磁电机,其反电动势一般为平顶波。注入谐波电流后,转矩脉动幅值将上升。例如,由图3可知R=0.25和R=0时样例电机的转矩脉动分别为1.9%、1.3%。因此,在电机设计时应注意抑制高次反电动势谐波。此外,齿槽转矩影响转矩脉动,本文对此不作分析。 3.1 用绕组函数法分析磁动势 绕组磁动势可通过绕组函数法进行分析[20]。本文将定子槽内绕组等效为槽中心的一点,并将坐标原点取在第A相绕组的起始点上,则第i相绕组函数可用傅里叶级数表示为 (14) 式中,Nk为第i相绕组函数的第k次谐波幅值;φ为空间机械角度。如果对第i相绕组注入如式(2)一样的电流,且该电流重新可用傅里叶级数表示为 (15) 式中,θ为电流角。此时,电机合成磁动势可表示为 (16) 考虑到电机绕组函数只含奇次谐波分量,则可能存在的磁动势谐波的次数满足如下关系 k=2n1m±v (17) 3.2 谐波电流对绕组磁动势的影响 由式(14)和式(15)可知,对m相表贴式集中绕组永磁电机注入v 3.3 例证 以样例电机为例,得到如图4a所示的电机A相绕组函数。对绕组函数进行傅里叶分解,得到如图4b所示的磁动势谐波分布。可见,相绕组磁动势不含第20n1(槽数的倍数)次的谐波分量,且各次谐波幅值周期性递增然后递减,总趋势是幅值随谐波次数增加而减少。 图4 电机绕组函数和相磁动势Fig.4 The winding function and phase MMF of machine 由相磁动势组合得到样例电机某一时刻的合成绕组磁动势如图5a所示,其谐波分布如图5b所示。图5对比了R=0和R=0.25两种情况。可见: 1)当相电流只含基波时,磁动势谐波的次数为k=10n1±1。如图5b所示,不考虑更高次分量,磁动势包括第1、9、11、19、21、29、31等次的谐波。 2)当相电流含v<5的谐波电流时,磁动势谐波的次数为k=10n1±1,10n1±3。如图5b所示,相对于基波电流,此时磁动势还包括第3、7、13、17、23、27、33等次的谐波。在新产生的谐波分量中,第3、7次谐波属于低次分量。该谐波对电机的涡流损耗影响较大[21,22]。同时,由于谐波次数增多,电机力波分布也将受到影响。 图5 电机合成磁动势Fig.5 The composite MMF of machine 绕组函数分析法得到的磁动势可通过有限元法计算的电枢反应磁场进行验证。本文采用有限元分析法对电机在电流分别为R=0和R=0.25情况下的电枢反应磁场进行计算,结果如图6所示。其中,图6a为电枢反应气隙磁场,磁场受定子开槽影响出现畸变,图6b为电枢反应磁场的谐波分布。图6表明,电枢反应磁场谐波情况与绕组磁动势谐波分布情况接近,说明采用绕组函数法分析电机磁动势是合理的。此外,注入谐波电流将会改变电枢反应磁场的谐波分布情况。当该磁场出现低次谐波分量时,将会对电机的性能造成不容忽视的影响。 图6 电机电枢反应气隙磁场Fig.6 The air-gap field due to armature reaction 由于谐波电流改变电枢反应磁场的谐波分布,电机性能将会受到明显影响。本节分析样例电机的涡流损耗和力波分布在谐波电流注入前后的变化。 4.1 对涡流损耗的影响 简化的涡流损耗标幺值计算模型指出[22] (18) 式中,ξ为第v次磁动势谐波的波长。 式(18)说明,磁动势谐波波长越长,永磁体涡流损耗越大。磁动势的低次谐波分量波长较长,是永磁体涡流损耗的主要诱因。图7给出了0~2倍额定转速范围内,样例电机在注入谐波电流前后的涡流损耗的有限元计算结果。可看到: 1)整个转速范围内,电机注入谐波电流后的涡流损耗比之前的都大。这主要是因为注入谐波电流后磁动势谐波分量,特别是第3、7次分量有明显增加。此外,随着转速增加,损耗的相对差别越小:注入谐波电流前后涡流损耗之比由100 r/min时的76.1%逐渐上升到1 200 r/min时的79.4%。 2)在整个转速范围内,无论是否注入谐波电流,电机的涡流损耗均随转速的增加而加大。这是因为涡流的频率随电机转速增加而增大。涡流功率越大,越易造成永磁体发热升温,甚至去磁。 图7 电机永磁体涡流损耗Fig.7 The permanent magnet eddy loss of machine 因此,多相分数槽集中绕组永磁电机注入谐波电流时,需注意采取措施抑制涡流损耗。比如,如果永磁体轴向长,可进行轴向分段。 4.2 对径向力波分布的影响 对于分数槽集中绕组电机,电磁振动问题需得到重视[23]。造成电磁振动的主要因素是径向力波分布[7]。径向力波可表示为[24] (19) 式中,μ0为真空磁导率;Br为径向气隙磁密;Bt为切向气隙磁密;frmv为径向力波谐波幅值;q为径向力波的模数。 一般而言,Bt远小于Br,计算时可忽略。另外,由于电磁振动的幅度与q4呈反比[23],分析电磁振动的变化情况时主要考虑低模数分量。 分析注入谐波电流对电机径向力波分布的影响,首先用有限元计算永磁体和绕组相互作用产生的磁通密度。需要注意的是,在注入谐波电流前后,绕组产生的径向力波发生改变,永磁体产生的径向力波则保持不变。再用式(19)得到力波分布如图8所示。可见注入谐波电流后: 1)模数为2的径向力波分量变为原来的109.3%。这主要是由于注入谐波电流后绕组产生的磁通密度出现了第3次分量,该次磁通密度与第1次磁通密度相互作用使得模数为2的力波增加。 2)出现了模数为4的力波分量。注入谐波电流前,该模数的力波幅值可忽略不计。注入谐波电流后绕组产生的磁密出现了第3、7次分量,这两种低次磁通密度相互作用使得模数为4的力波出现,且幅值为模数为2的力波的24.95%。 图8 电机径向力波密度Fig.8 The radical force density of machine 因此,注入谐波电流会增大电磁振动的幅值,加剧电磁振动乃至噪声现象。这说明,对于需要采用谐波注入方式的多相电机而言,尤其需要研究抑制电磁振动的方法。 对多相分数槽集中绕组表贴式永磁电机注入谐波电流,将对电机的性能造成较全面的影响。在电机设计、运行时,需注意: 1)优化设计参数,增大次数低于相数的反电动势分量,抑制次数高于相数的反电动势谐波分量,以提升转矩性能。为此,建议优化槽极配合或绕组结构以提高基波和谐波绕组系数[25],并对永磁体形状进行优化[17-19]。 2)采用谐波注入法提升平均转矩时,在确保相电流的有效值相等以保证铜耗不变的前提下,相电流谐波比例与对应的反电动势谐波比例应保持一致,以获得最大平均转矩。 3)可采用解析法确定具体电机的反电动势,进而确定最佳的谐波电流比例。 4)注入谐波电流将会导致绕组磁动势出现新的谐波次数,原有的谐波分量幅值也可能增大。当新出现或增大了的谐波属于低次谐波时,电机的涡流损耗、低模数的径向力波分量将增大。因此,对采用谐波注入方式的多相电机而言,需研究并采取诸如永磁体分段、槽极配合遴选等抑制涡流损耗和电磁振动的方法,避免可能的损害。 [1] Levi E.Multiphase electric machines for variable-speed applications[J].IEEE Transactions on Industry Electronics,2008,55(55):1893-1909. [2] 王东,马伟明,郭云珺,等.基于非正弦供电方式的多相感应电动机建模[J].电工技术学报,2010,25(2):6-14. Wang Dong,Ma Weiming,Guo Yunjun,et al.Modeling of multiphase induction motor with non-sinusoidal supply[J].Transactions of China Electrotechnical Society,2010,25(2):6-14. [3] EL-Refaie A M.Fractional-slot concentrated windings synchronous permanent magnet machines:opportunities and challenges[J].IEEE Transaction on Industry Applications,2010,57(1):107-121. [4] 郭思源,周理兵,齐歌.双三相永磁同步电机电磁性能解析计算[J].电工技术学报,2014,29(5):17-28.Guo Siyuan,Zhou Libing,Qi Ge.Analytical calculation of electromagnetic performance in dual three-phase permanent magnet brushless AC machines[J].Transactions of China Electrotechnical Society,2014,29(5):17-28. [5] 唐骏,王铁成,崔淑梅.五相逆变系统的SVPWM实现方法[J].电工技术学报,2013,28(7):64-72. Tang Jun,Wang Tiecheng,Cui Shumei.Implementation method of SVPWM for five-phase inverters[J].Transactions of China Electrotechnical Society,2013,28(7):64-72. [6] Bianchi N,Dai Pré M,Alberti L,et al.Theory and design of fractional-slot PM machines[M].Padova,Italy:CLEUP,2007. [7] Valavi M,Nysveen A,Nilssen R,et al.Influence of pole and slot combinations on magnetic forces and vibration in low-speed PM wind generators[J].IEEE Transactions on Magnetics,2014,50(5):1-11. [8] 方程,许海平,薛劭申,等.直驱型多相永磁同步电机转矩脉动及损耗特性[J].电工技术学报,2014,29(5):149-159. Fang Cheng,Xu Haiping,Xue Shaoshen,et al.Torque ripple and loss of direct-drive multi-phase permanent magnet synchronous machines[J].Transactions of China Electrotechnical Society,2014,29(5):149-159. [9] 方程,许海平,薛劭申,等.直驱型多相永磁同步电机定子磁动势与气隙磁密特性分析[J].中国电机工程学报,2013,33(24):106-113. Fang Cheng,Xu Haiping,Xue Shaoshen,et al.Analysis of stator MMF and air gap flux density characteristics of direct-drive multi-phase permanent magnet synchronous machines[J].Proceedings of the CSEE,2013,33(24):106-113. [10]赵品志,杨贵杰,李勇.三次谐波注入式五相永磁同步电机转矩密度优化[J].中国电机工程学报,2010,30(33):71-77. Zhao Pinzhi,Yang Guijie,Li Yong.Torque density optimization for five-phase PMSM with third harmonic injection[J].Proceedings of the CSEE,2010,30(33):71-77. [11]Leila P,Hamid A T.Five-phase permanent-magnet motor drives[J].IEEE Transactions on Industry Applications,2005,41(1):30-37. [12]Wang Jin,Zhou Libing,Qu Ronghai.Harmonic current effect on torque density of a multiphase permanent magnet machine[C].2011 International Conference on Electrical Machines Systems (ICEMS),Beijing,2011,1-6. [13]Semail E,Kestelyn X,Bouscayrol A.Right harmonic spectrum for the back-electromotive force of a n-phase synchronous motor[C].IEEE Industrial Application Society Annual Meeting,Seattle,USA,2004,1-8. [14]Abdel-Khalik A,Masoud M,Williams B.Improved flux pattern with third harmonic injection for multiphase induction machines[J].IEEE Transactions on Power Electronics,2012,27(3):1563-1578. [15]Kestelyn X,Semail E.A vectorial approach for generation of optimal current references for multiphase permanent-magnet synchronous machines in real time[J].IEEE Transactions on Industrial Electronics,2011,58(11):5057-5065. [16]Shen Y,Liu G,Xia Z P,et al.Determination of maximum electromagnetic torque in PM brushless machines having two-segment halbach array[J].IEEE Transactions on Industrial Electronics,2014,61(2):718-729. [17]Scuiller F.Magnet shape optimization to reduce pulsating torque for a five-phase permanent-magnet low-speed machine[J].IEEE Transactions on Magnetics,2014,50(4):1-9. [18]Wang K,Zhu Z Q,Ombach G.Torque enhancement of surface-mounted permanent magnet machine using 3rd order harmonic[J].IEEE Transactions on Magnetics,2014,50(3):104-113. [19]Wang K,Zhu Z Q,Ombach G.Torque improvement of five-phase surface-mounted permanent magnet machine using 3rd order harmonic[J].IEEE Transactions on Energy Conversion,2014,29(3):735-747. [20]Toliyat H,Xu L,Lipo T A.A five-phase reluctance motor with high specific torque[J].IEEE Transactions on Industry Applications,1992,28(3):659-667. [21]Fornasiero E,Bianchi N,Bolognani S.Slot harmonic impact on rotor losses in fractional-slot permanent-magnet machines[J].IEEE Transactions on Industrial Electronics,2012,59(2):2257-2564. [22]Bianchi N,Fornasiero E.Impact of MMF space harmonic on rotor losses in fractional-slot permanent-magnet machines[J].IEEE Transactions on Energy Conversion,2009,24(2):323-328. [23]Jacek F G,Chong W,Joseph C L.Noise of polyphase electric motors[M].Boca Raton:CRC Press,2006. [24]Zhu Z Q,Xia Z P,Wu L J,et al.Analytical modeling and finite-element computation of radial vibration force in fractional-slot permanent-magnet brushless machines[J].IEEE Transactions on Industry Applications,2010,46(5):1908-1918. [25]Chen Yiguang,Du Zhiming,Zhong Weigang,et al.Modular stator structure permanent magnet synchronous machine[C].World Automation Congress,Hawaii,HI,2008:1-5. Harmonic Currents Determination and Their Impacts on Multiphase Fractional-slot Concentrated Winding Surface-mounted Permanent Magnet Machine KangHuilinZhouLibingWangJinPengXi (State Key Laboratory of Advanced Electromagnetic Engineering and Technology Huazhong University of Science and Technology Wuhan 430074 China) A five-phase 20-slot 22-pole fractional-slot concentrated winding multiphase surface-mounted permanent magnet machine is exemplified to study the influence of the injected harmonic currents.The optimal harmonic current component is analytically derived to achieve the maximum average torque while the effective values of the phase currents are kept unchanged.The analytical current is verified by finite element analysis.Further,comparisons of electromagnetic torque,magneto-motive force,air-gap flux density,eddy current loss,and radial force density between the machines with and without harmonic current injection are respectively carried out.The results show that new space harmonics including the ones with lower orders appear due to the injected harmonic current,which leads to the increases of the eddy current loss and the lowest order radial force.The results demonstrate the key points and guidance for the multiphase permanent magnet machine design. Multiphase permanent magnet machine,harmonic current,electromagnetic performance,impact 国家自然科学基金面上项目(51177056)和国家自然科学基金青年科学基金(51307067)资助项目。 2014-12-02 改稿日期2015-03-06 TM315 康惠林 男,1986年生,博士研究生,研究方向为多相永磁电机的分析和驱动。(通信作者) 周理兵 男,1961年生,教授,博士生导师,研究方向为新型电机的运行理论和控制。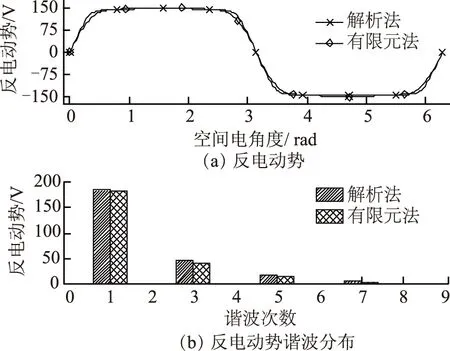
2 谐波电流对转矩的影响
3 谐波电流对绕组磁动势的影响
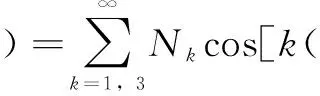
4 谐波电流对涡流损耗和力波的影响

5 结论

