双三相异步电机电流预测控制算法

张 杰 柴建云 孙旭东 陆海峰

(电力系统及发电设备安全控制和仿真国家重点实验室(清华大学) 北京 100084)



双三相异步电机电流预测控制算法

张 杰 柴建云 孙旭东 陆海峰

(电力系统及发电设备安全控制和仿真国家重点实验室(清华大学) 北京 100084)

针对一种半对称式双三相异步电机，提出两种电流预测控制算法。一种为基本算法，另一种为在基本算法的基础上通过引入合理近似而实现的模块化算法。相对而言，后者更为简洁，且易于在其他一些结构更为复杂的多相电机中进行推广。此外，针对离散控制的延时对上述两种算法带来的稳定性问题进行分析，并给出改进方案。实验结果表明，两种电流预测控制算法均能实现良好的电流控制效果，同时该文针对稳定性问题的改进方法也是有效的。

双三相异步电机 电流预测控制 模块化 稳定性

0 引言

多相电机因具有转矩脉动小、单个功率器件电流容量要求小、可容错运行等优点，得到越来越广泛的应用[1，2]。多相电机种类众多，其中有一类为多Y型结构，即电机定子绕组由多组相互间错开一定角度的三相绕组单元构成，如半对称式双三相电机[3]、四Y移15°十二相电机[4]等。

为了充分发挥多相电机的优势，学者们从多相电机的高性能控制算法的角度开展了大量工作[5，6]。然而，对于控制算法中的电流内环，大多数学者只是简单地给出PI调节器的方案。对于三相电机，尽管已有PI调节器参数的设计方法[7]，但设计出的参数应用于实际系统时，往往需要根据不同工况做较大幅度的调整。而对于多相电机，尚未有学者给出系统化的PI调节器参数的设计方法。此外，随着多相电机系统复杂程度的提高和PI调节器数目的增加，通过实际调试获得一组性能良好的PI参数也变得较为困难。为此，一些学者考虑了其他形式的电流调节器。以半对称式双三相异步电机为例，文献[8]采用了滞环比较器的方法，但存在开关频率不固定的缺点。文献[9]提出了使用PR调节器的思路，但仍面临PR参数的整定问题。F.Barrero等[10-15]将电流预测控制(predictive current control，PCC)算法应用于电流内环，在获得良好的电流控制效果的同时，降低了参数整定困难。PCC的数学本质是从可行解中寻找最优解的优化问题，按可行解的构成大致可分为两类：一类是由逆变器开关状态决定的有限个电压矢量组成可行解；另一类是考虑SVPWM方案后，将逆变器电压输出限幅内所有的电压值作为可行解。F.Barrero等选择的是第一类思路。在双三相异步电机领域，尚未有学者采用第二类思路。对于双三相异步电机，每个控制周期需要考虑的电压矢量从三相系统的8个增加至64个，运算压力大大增加。文献[10-15]的主要工作之一即为降低算法运算量。文献[10，11]采用动态减少每个周期的可选电压矢量数目的方案，文献[12-15]直接将可选电压矢量子集限定为12个最大电压矢量和零矢量。文献[10-15]的策略降低了PCC算法的运算量，获得了良好的电流动态响应，但其电流高频纹波还较大，尤其是谐波子空间电流的纹波水平还有待改善。

实际上，如果采用PCC算法的第二类思路，算法的运算量将近似随电机相数增加呈线性增长，而非第一类思路的指数增长。并且对于谐波子空间的电流，也易于通过合理计算电压指令而实现纹波更小的控制效果。本文首先基于PCC算法的第二类思路，提出双三相异步电机的一种基本PCC算法。在此基础上，考虑到双三相异步电机绕组构成方面具有模块化特点，为使算法更为简洁，对电机模型引入了模块化的合理近似，将双三相异步电机近似按两个独立运行的三相异步电机模块进行建模，通过分别实现每个模块的PCC来实现双三相异步电机整体的PCC。此外，还对这两种PCC算法的稳定性问题进行了一处分析和改进。最后通过实验研究，对比本文提出的两种PCC算法和文献[15]的PCC算法的电流控制效果，并验证本文对PCC算法稳定性的一处改进的有效性。

1 双三相异步电机的基本PCC算法

1.1 双三相异步电机的数学模型

双三相异步电机的绕组示意图如图1所示。在定子侧，abc三相绕组Y型联结，uvw三相绕组亦Y型联结。abc三相绕组在空间位置上超前uvw三相绕组30°电角度，且两套绕组的中性点相互隔离。两套绕组没有电的耦合，再忽略两套定子绕组的互漏感，则两套绕组仅通过气隙磁链发生磁的耦合。

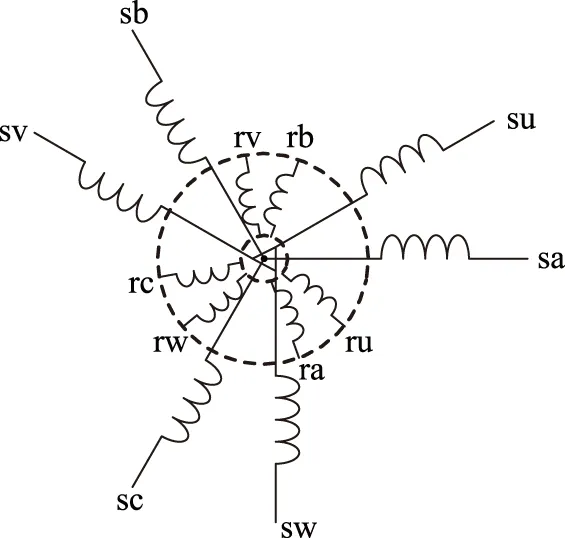
图1 双三相异步电机绕组示意图Fig.1 Schematic of the windings of the dual three phase induction machine

采用文献[3]提出的空间矢量分解方法对双三相异步电机进行建模。其中，所用坐标变换式如式(1)所示

(1)

式中，x表示电压u、电流i和磁链ψ等电气量；xsa、xsb、xsc、xsu、xsv、xsw分别表示定子a、b、c、u、v、w各相的电气量；xsα、xsβ、xsz1、xsz2分别表示在定子基波子空间的α轴和β轴及谐波子空间z1轴和z2轴分量。

将文献[3]中的电机模型改写为电阻，电感和反电势串联的形式[16]为

(2)

其中

(3)

式中，Rs、Rr、Lm、Lr、σLs、Lsl、Tr分别为电机的定子电阻、转子电阻、互感、转子电感、定子暂态电感、定子漏感和转子时间常数；ψrα、ψrβ、ωr分别为电机的转子αβ轴磁链和转速。

1.2 基本PCC算法的实现

对式(2)所示的电机方程采用梯形公式，以Ts为控制周期，假定当前为n时刻，进行离散化，其结果如式(4)所示。其中，为了便于对反电势的估计，将梯形公式离散化时的[eα(n)+eα(n-1)]/2和[eβ(n)+eβ(n-1)]/2分别用eα(n)和eβ(n)代替。

(4)

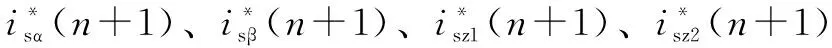
(5)

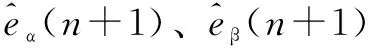
(6)

采用上述方法处理后，当前n时刻的电流采样值将完全不出现在表达式中。这样，综合式(4)～式(6)，并用反电势的预测值代替实际值，最终可得到本文提出的基本PCC算法中电压指令的表达式为

(7)

文献[15]中基于有限开关状态的PCC算法需要对每个可选电压矢量进行一次计算，而本文方法只需要依据式(7)进行一次运算，运算量得到降低。由于式(7)是以下一周期实际电流跟踪指令电流为依据进行电压指令的计算，因而从电流的控制效果看，该方法优于以电流偏差最小为目标，在有限个电压矢量中进行选择的方法。

2 双三相异步电机的模块化PCC算法

2.1 双三相异步电机的模块化模型

分别取a相绕组轴线和u相绕组轴线为α轴和α′轴，β轴和β′轴分别由α轴和α′轴逆时针旋转90°得到。两套绕组分别以αβ轴和α′β′轴做clarke变换，如式(8)、式(9)

(8)

(9)

式中，x表示电压u、电流i和磁链ψ等电气量；xsα1、xsβ1、xsα′2、xsβ′2分别表示第一套绕组的电气量x在定子αβ轴的分量和第二套绕组的电气量x在α′β′轴的分量。对式(9)取式(10)所示的park变换，将第二套绕组在α′β′轴的电气量变换到αβ轴。

(10)

双三相异步电机稳态对称运行时，时间上abc三相电流分别超前uvw三相30°，幅值上各相电流均相等，电压和磁链的情况相同。而式(10)的另一个物理含义是分别将uvw相的电气量的相位增加了30°，从而使得变换后的结果xsα2、xsβ2分别与xsα1、xsβ1的相位相同，幅值相同。综合式(1)、式(8)、式(10)可得到

(11)

将式(11)的结果代入式(2)中可得

(12)

定义下述两个变量

(13)

则式(12)可转换为

(14)

(15)

考虑到电机两套绕组结构参数相同且运行对称的条件，近似有isα1=isα2，isβ1=isβ2，且pisα1=pisα2，pisβ1=pisβ2，则式(14)和式(15)分别转换为

(16)

(17)

式(16)、式(17)即为双三相异步电机的模块化模型。下面给出上述近似处理的合理性：

2)近似处理带来的偏差可归结为电机模型的外界干扰项。PCC算法是一种电流闭环控制算法，对外界扰动具有良好的抑制能力，在实现电流闭环控制时，能够抑制模型近似化处理所带来的偏差。

2.2 模块化PCC算法的实现

(18)

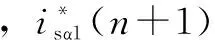
模块化PCC算法使得PCC算法在由三相绕组为单元组成的多相电机中实现更为简洁，且软件上的模块化将为硬件上的模块化奠定基础。本文的后续实验将表明，尽管采用了一定的近似处理，模块化的PCC算法能获得与基本PCC算法基本一致的电流控制效果。

3 考虑稳定性问题后对PCC算法的改进

PCC算法的稳定性一般会受到离散控制的延时和参数偏差等两方面因素的影响。双三相异步电机的PCC算法主要使用的是定转子的漏感参数，其在电机运行过程中，受铁心饱和程度变化的影响较小，因而本文主要考虑离散控制的延时带来的稳定性问题。讨论稳定性问题一般需得到系统的传递函数，且传递函数中涉及的变量应能连续取值。对于文献[15]中基于有限开关状态的PCC算法，推导其传递函数的过程较为复杂，且涉及的电压变量取值不连续，难以进行稳定性分析和改进，而本文提出的两种PCC算法则不存在上述困难。

在分析PCC算法的稳定性问题时，一般认为电机的反电势得到了准确预测，电压指令计算式，即控制器模型和电机模型中的反电势部分可相互抵消，不再考虑。在此基础上，静止坐标系中电机模型和控制器模型在不同坐标轴中分别具有相同的形式，因而仅以其中一个坐标轴的方程为例进行分析即可。

不考虑反电势，取其中一个坐标轴的电机模型进行Z变换后为

(19)

对一个坐标轴的控制器模型进行Z变换后为

(20)

综合式(19)和式(20)可得

(21)

一般有ReTs≪Le[17]，因而式(21)的极点趋近于0，为稳定系统，综合式(19)和式(21)，考虑U(z)与I*(z)的关系为

(22)

式(22)的极点除式(21)外的两个接近0的极点外，还存在一个单位圆上的极点-1，因而系统临界稳定，实际运行时则较易进入不稳定状态。这就意味着尽管I(z)可以跟随I*(z)，但U(z)会出现幅值不断增大的振荡情况。

为解决该稳定性问题，本文首先从稳态入手，考虑到u(n+1)，u(n)和u(n-1)之间在稳态时相差较小的特点，提出一种在PCC算法中用u(n+1)部分代替u(n)和u(n-1)的策略，来保证系统的稳定性。在确保算法的稳定性后，再考虑电流的控制效果是否仍能满足要求。

采用该方法后，PCC算法的控制器模型由式(20)转换为

(23)

式中，k1、k2分别表示u(n+1)代替u(n)和u(n-1)的比例。综合式(19)和式(23)，并忽略包含ReTs/Le的项，可得此时U(z)与I*(z)的关系式为

(24)

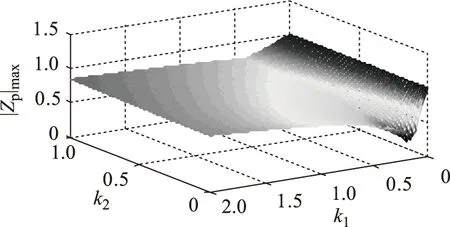
图2 模最大极点的模与k1、k2的关系图Fig.2 Relationship between the magnitude of the largest magnitude pole and k1、k2

观察图2可知，理论上只要取k1略大于0，模最大极点的模就小于1，系统进入稳定区域。实际中，需要为系统留有一定稳定裕度，因而k1、k2取值不能过小。图3a给出了k2取0.1，k1取0.1～0.6时，H(z)=[Ts/(2Le)]×(U(z)/I*(z))的幅频特性，其中离散周期Ts取 0.2 ms。可看出，在频率较高的区域，H(z)幅值较大，且在2.5kHz处存在一个尖峰。H(z)在高频区域较高的幅值会将反馈回路中的高频扰动进行放大，对系统的稳定产生不利影响。随着k1的增大，该尖峰逐渐降低，当k1大于0.4后，尖峰的减小已不再明显。图3b给出了k1取0.4，k2取0～0.4时，H(z)的幅频特性。可看出，随着k2的增加，尖峰有所变窄，但不改变2.5 kHz时的取值，且当k2大于0.1后，对尖峰的改善已不是很明显。综合上述考虑，本文在下文的实验中取k1=0.4，k2=0.1。在实际中，该取值还可进行调整，但总体取值范围不会变化很大。

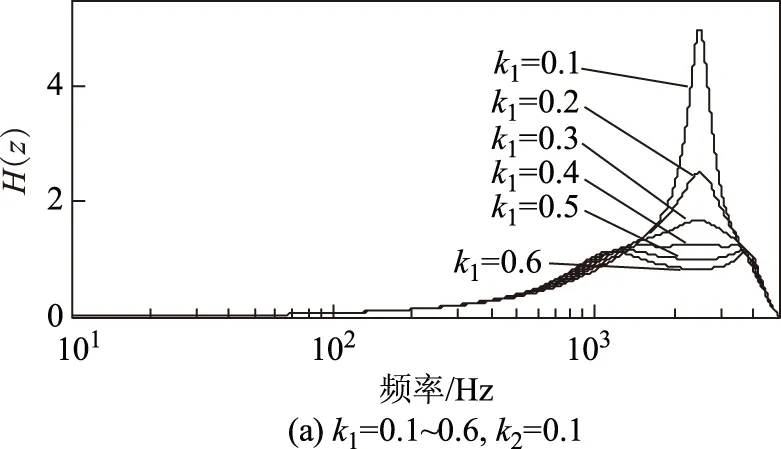
图3 (Ts/2Le)(U(z)/I*(z))的幅频特性与k1、k2的关系图Fig.3 Relationship between the magnitude-frequency characteristic of (Ts/2Le)(U(z)/I*(z)) and k1、k2

采用上述改进策略后，实际电流与指令电流间的关系由式(21)转换为式(25)，该式已忽略包含ReTs/Le的项。其伯德图如图4所示。图4表明，采用上述方法改善稳定性后，仍能保证电流响应的带宽在1 kHz以上，且对于最为关注的0～150 Hz范围内的电流，其幅值衰减和相位滞后几乎为0，因而总体上可认为电流响应仍满足要求。

(25)

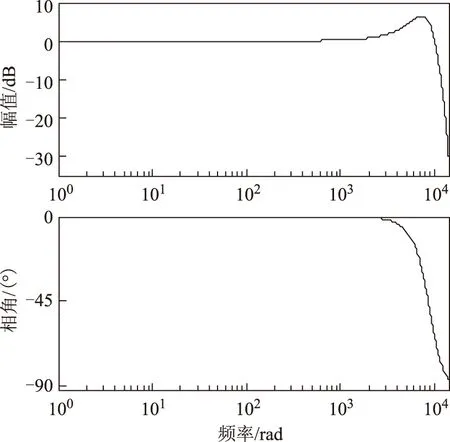
图4 采用本文策略后，I(z)/I*(z)关系式的伯德图Fig.4 The Bode diagram of I(z)/I*(z) with the proposed method

4 实验结果

实验在一台2.5 kW双三相异步电机机组上完成。电机参数见表1。实验平台如图5所示。在图5a中，该电机同轴连接了一台由安川H1000型四象限变频器控制的三相异步电机作为负载。在图5b中，由两套三相逆变器主电路构成双三相逆变器的主电路，控制板选用TMS320C2812DSP，开关频率5 kHz。实验过程中利用CAN总线以5 kHz速率读取并记录DSP芯片内部的电流电压等相关数据。

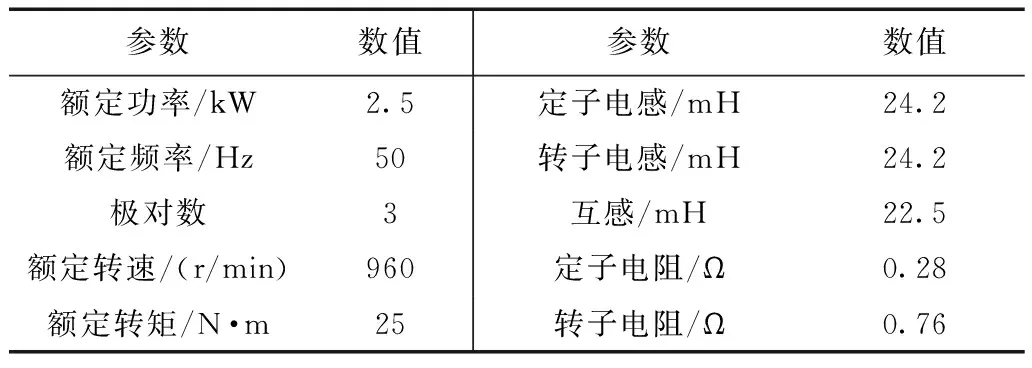
表1 实验用双三相异步电机参数Tab.1 Parameters of dual three phase induction machine

图5 实验平台Fig.5 Experimental platform

本文实验采用间接矢量控制方案，图6给出了模块化PCC算法的控制框图。两套绕组均分整个系统的转矩电流指令和励磁电流指令。两套系统各自独立实现自己的电流预测控制算法。对于基本PCC算法的控制框图，其与传统的双三相异步电机矢量控制框图类似，只需将电流PI调节器用预测电流控制器代替即可。

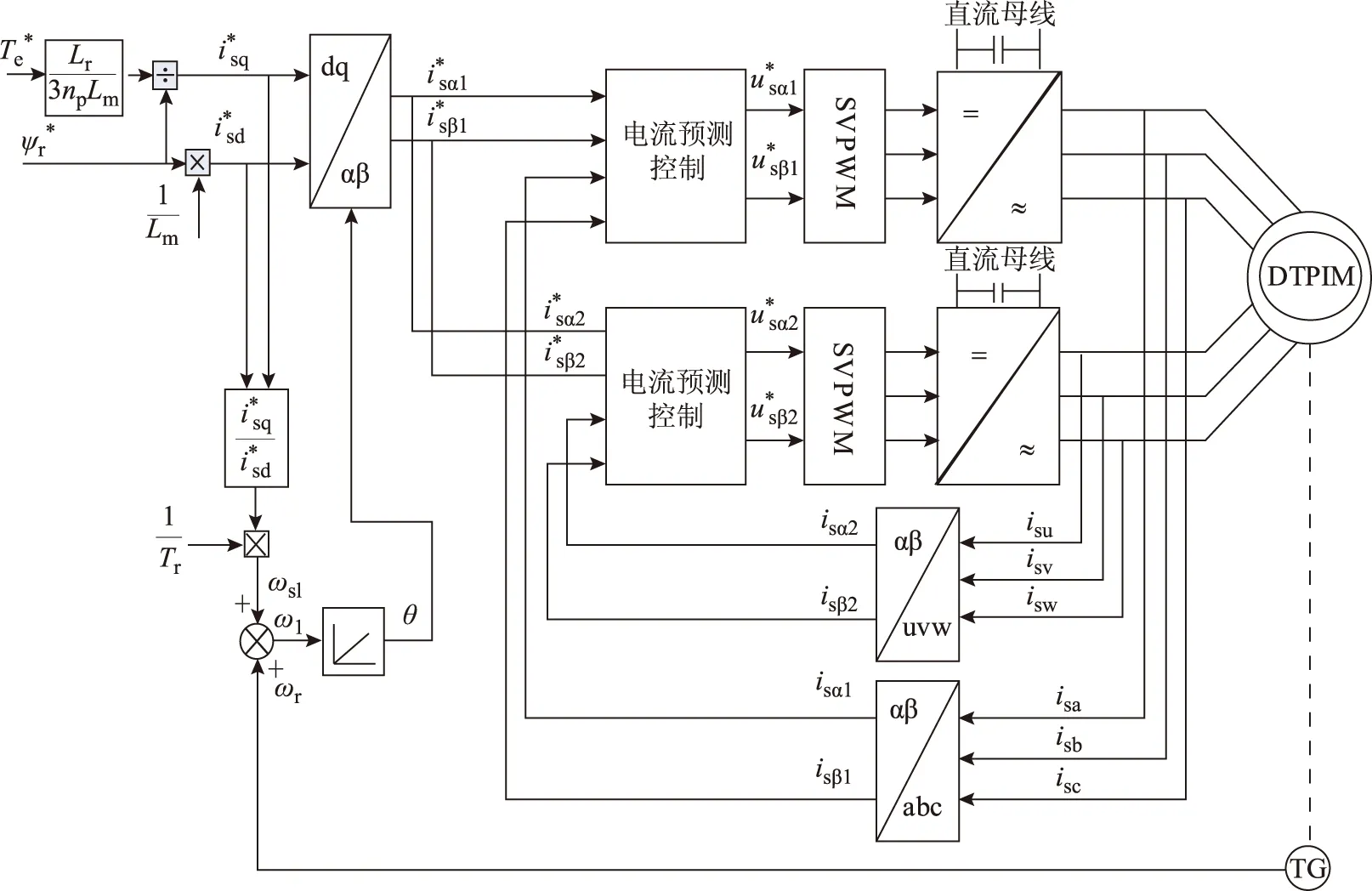
图6 实验系统框图Fig.6 Diagram of the experimental system

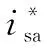
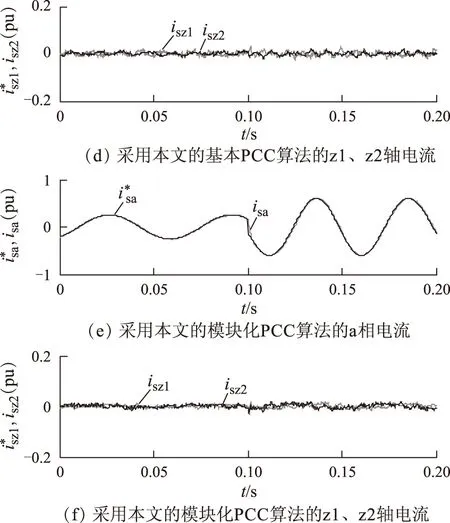
图7 3种电流预测控制算法的对比实验结果Fig.7 Experimental results with the three PCC strategies

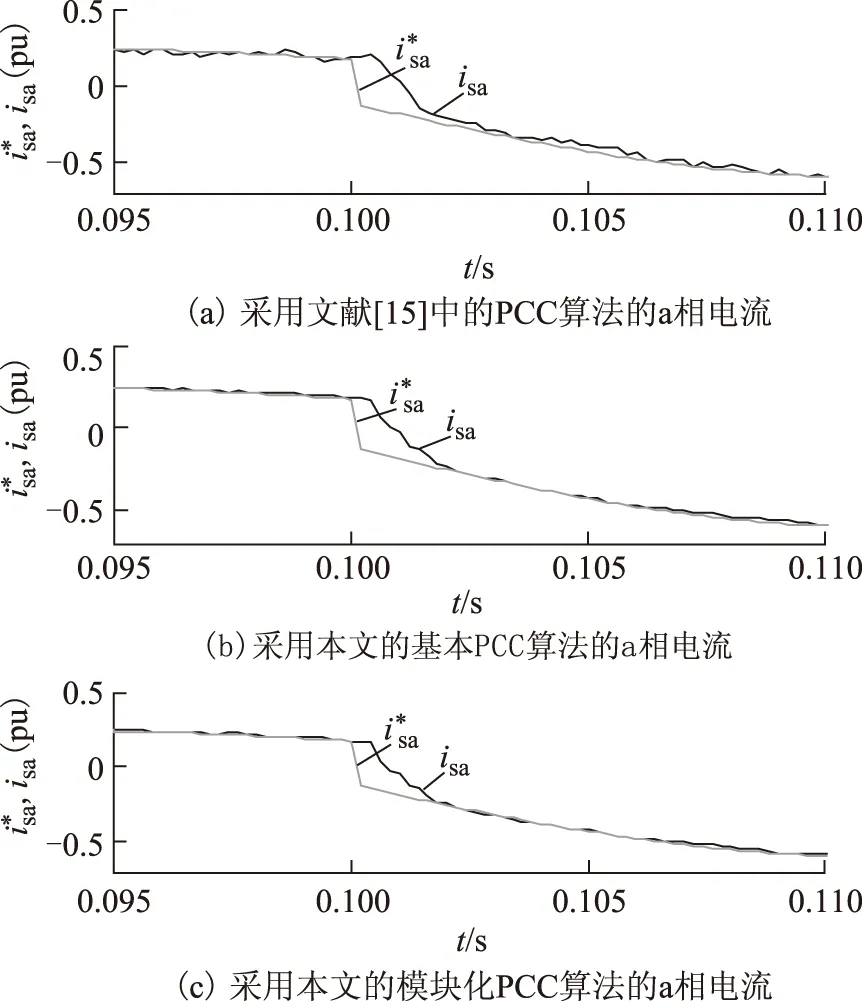
图8 3种电流预测控制算法对比实验结果(局部放大图)Fig.8 Experimental results with the three PCC strategies (partial enlarged view)

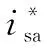
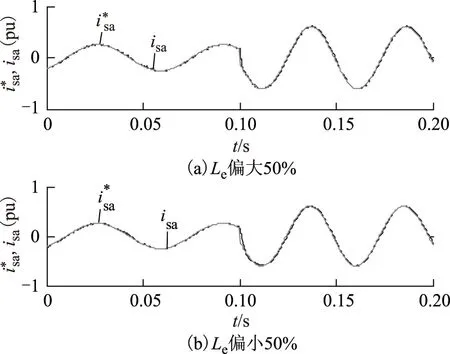
图9 参数有偏差时，模块化PCC实验结果Fig.9 Experimental results of the proposed modularized PCC strategy with inaccurate machine parameter

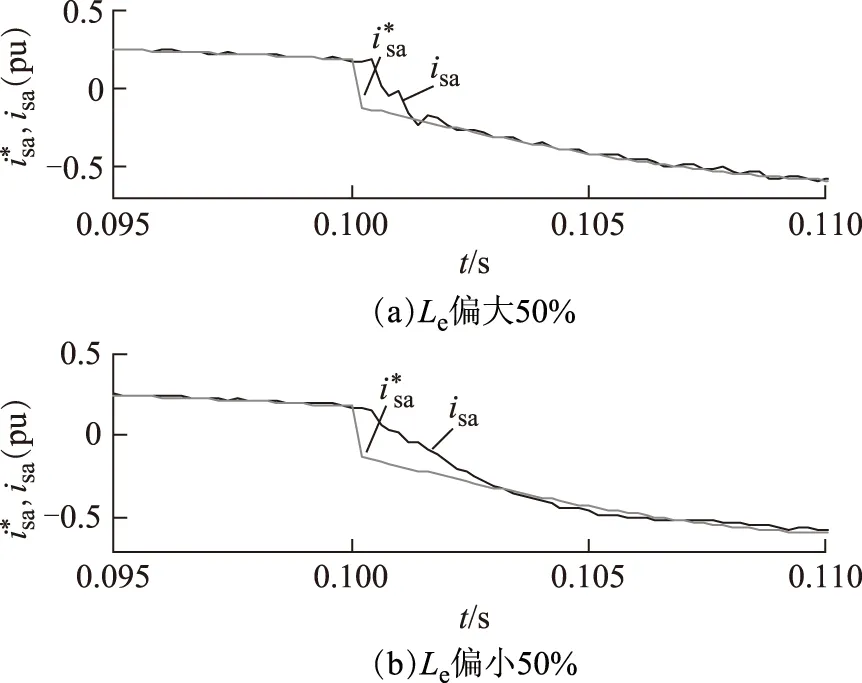
图10 参数有偏差时，模块化PCC实验结果(局部放大图)Fig.10 Experimental results of the proposed modularized PCC strategy with inaccurate parameter (partial enlarged view)

为了验证第3节中关于稳定性问题的分析的正确性，本文给出了从稳定状态向不稳定状态过渡的实验结果，如图11所示。在该实验中，电流指令不变，修正系数k1和k2分别由0.4和0.1逐渐减少至0。为使在系统失控状态电流不会严重过电流，对输出电压取0.3 pu的限幅值。在0～0.2 s范围内，k1和k2取前文的设定值，电流控制效果良好。在0.2～0.8 s范围内，随着k1和k2逐渐减小，图11a的abc绕组的α轴电流波形isα1和图11b的abc绕组的α轴电压波形usα1均出现了明显的高频脉动，但电流并未完全失控。在0.8 s之后，k1和k2均减小为0，电流完全失控。该实验结果表明，如果取k1=k2=0，即不采用改善稳定性的方法，PCC算法将不稳定。而k1取略大于0的值即可使算法稳定，但为确保足够的稳定裕度，k1、k2取值不可过小。

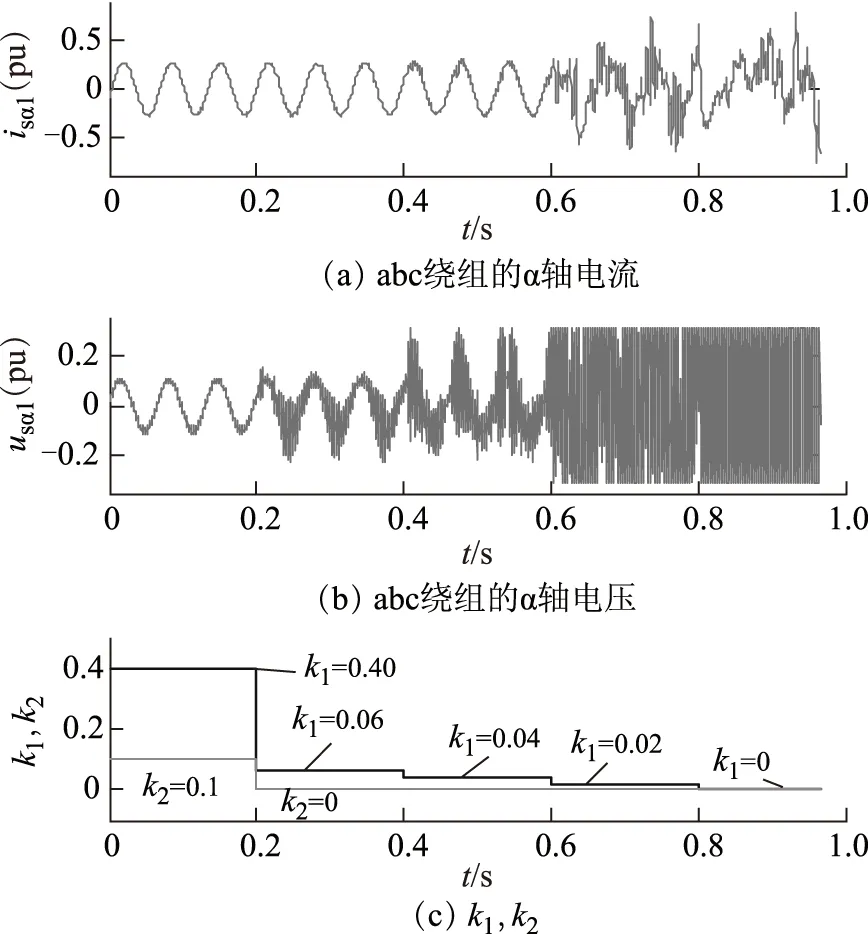
图11 随k1，k2变化，从稳定过渡到不稳定的对比实验结果Fig.11 Comparison experimental results of transition from stable to unstable conditions with the change of k1 and k2

5 结论

本文针对双三相异步电机，提出了基本PCC算法和模块化PCC算法两种电流控制算法。在运算量有所减少的前提下，两种算法实现了与文献[15]中性能最优的一种PCC算法基本一致的动态性能，并且在减小电流纹波，尤其是谐波子空间的电流纹波方面有明显改进。本文的模块化PCC算法相对于基本PCC算法，采用了含有一定近似处理的模块化电机模型。相关分析和实验表明，该近似不会明显影响PCC算法的性能。而模块化PCC算法的思路更为简洁，并可在其他一些绕组结构具有模块化特点的多相电机中加以推广。此外，本文针对基本PCC算法和模块化PCC算法的稳定性问题的一处分析和改进的有效性也通过一组实验得到了验证。

[1] Levi E.Multiphase electric machines for variable-speed applications[J].IEEE Transactions on Industrial Electronics，2008，55(5)：1893-1909.

[2] 庄朝晖，熊有伦，马挺.多相感应电机变频调速系统——回顾、现状及展望[J].电气传动，2001，31(2)：3-7. Zhuang Zhaohui，Xiong Youlun，Ma Ting.Multiphase variable-speed induction machine drives system—state of arts and trends[J].Electric Drive，2001，31(2)：3-7.

[3] Zhao Yifan，Lipo Thomas A.Space vector PWM control of dual three-phase induction machine using vector space decomposition[J].IEEE Transactions on Industry Applications，1995，31(5)：1100-1109.

[4] 谢卫，朱军.十二相四Y移15°绕组同步电动机的数学模型及动态仿真[J].电工技术学报，2004，19(1)：2-6. Xie Wei，Zhu Jun.Modeling and simulation of 12-phase synchronous motor with four Y-connected 3-phase symmetrical windings displaced in turn by 15°[J].Transactions of China Electrotechnical Society，2004，19(1)：2-6.

[5] 杨金波，李铁才，杨贵杰.一相开路双三相永磁同步电机建模与控制[J].电工技术学报，2011，26(10)：167-173. Yang Jinbo，Li Tiecai，Yang Guijie.Modeling and control of dual three-phase PMSM with one open phase[J].Transactions of China Electrotechnical Society，2011，26(10)：167-173.

[6] Hatua K，Ranganathan V T.Direct torque control schemes for split-phase induction machine[J].IEEE Transactions on Industry Applications，2005，41(5)：1243-1254.

[7] 李永东.交流电机数字控制系统[M].北京：机械工业出版社，2012.

[8] Kianinezhad R，Nahid B，Baghli L，et al.Aspects of current regulation in indirect field oriented control of dual three phase induction machines[C].IEEE International Conference on Industrial Technology，Mumbai，India，2006：933-938.

[9] Bojoi R，Levi E，Farina F，et al.Dual three-phase induction motor drive with digital current control in the stationary reference frame[J].IEE Proceedings-Electric Power Application，2006，153(1)：129-139.

[10]Duran M J，Barrero F，Prieto J，et al.Predictive current control of dual three-phase drives using restrained search techniques and multi level voltage source inverters[C].2010 IEEE International Symposium on Industrial Electronics，Bari，Italy，2010：3171-3176.

[11]Duran M J，Prieto J，Barrero F，et al.Predictive current control of dual three-phase drives using restrained search techniques[J].IEEE Transactions on Industrial Electronics，2011，58(8)：3253-3263.

[12]Barrero F，Arahal M R，Gregor R，et al.A proof of concept study of predictive current control for VSI-driven asymmetrical dual three-phase AC machines[J].IEEE Transactions on Industrial Electronics，2009，56(6)：1937-1954.

[13]Barrero F，Arahal M R，Gregor R，et al.One-step modulation predictive current control method for the asymmetrical dual three-phase induction machine[J].IEEE Transactions on Industrial Electronics，2009，56(6)：1974-1983.

[14]Gregor R，Barrero F，Toral S L.Predictive-space vector PWM current control method for asymmetrical dual three-phase induction motor drives[J].IET Electric Power Applications，2010，4(1)：26-34.

[15]Barrero F，Prieto J，Levi E.An enhanced predictive current control method for asymmetrical six-phase motor drives[J].IEEE Transactions on Industrial Electronics，2011，58(8)：3242-3252.

[16]Quang N P，Dittrich J A.Vector control of three-phase AC machines[M].Berlin，Heidelberg：Springer，2008.

[17]Guzinski J，Krzeminski Z.Advanced current regulated PWM inverter with simplified load model[J].Electric Power Components and Systems，2004，32(10)：1031-1042.

Predictive Current Control Methods for Dual Three Phase Induction Machine

ZhangJieChaiJianyunSunXudongLuHaifeng

(State Key Laboratory of Security Control and Simulation of Power Systems and Large Generation Equipments Tsinghua University Beijing 100084 China)

For an asymmetrical dual three phase induction machine，two predictive current control methods are proposed.One of them is the basic method.Based on this，the other modularized method is suggested with reasonable assumption.Comparing to the basic method，the latter is more concise and easy to be applied to some other more sophisticated multi-phase machines.Besides，the stability issue of these two predictive current control strategies caused by the delay of the discrete control is analyzed，and one improvement solution is provided.Experimental results show that the two proposed predictive current control strategies can achieve a good current performance.Meanwhile，the effectiveness of the improvement on the stability issue is also validated.

Dual three phase induction machine，predictive current control，modularized，stability

国家自然科学基金(51277102)资助项目。

2014-11-15 改稿日期2015-03-12

TM321

张 杰 男，1987年生，博士研究生，研究方向为电动汽车驱动控制。(通信作者)

柴建云 男，1961年生，教授，博士生导师，研究方向为电机及其控制系统。