永磁同步电机转子初始位置检测方法
鲁家栋 刘景林 卫丽超
(西北工业大学自动化学院 西安 710129)
永磁同步电机转子初始位置检测方法
鲁家栋 刘景林 卫丽超
(西北工业大学自动化学院 西安 710129)
针对永磁同步电机转子初始位置检测已有方法存在的电机“抖动”、对电机参数依赖性强、高频电流信号数学处理算法复杂等问题,提出一种基于高频电压信号注入法的永磁同步电机转子初始位置检测方法。该方法通过对三相高频电压信号的电流响应进行低通滤波,比较三相电流响应幅值的大小关系,依据转子位置角θ对三相高频电流响应信号幅值的调制规律,得到电机转子初始位置信息,最后利用电机磁路饱和效应区分电机转子NS极性。理论分析及实验表明,该方法能准确检测出电机转子初始位置信息,电机转子不会发生“抖动”,检测方法对电机参数依赖性低,电流处理算法简单,不需要额外增加硬件电路,检测误差较小,可满足永磁同步电机的平稳起动要求。
永磁同步电机 转子初始位置 高频信号注入 磁路饱和效应
0 引言
在永磁同步电机控制中,若不能预知转子初始位置,就会出现转子短暂反转或失步而起动失败。绝对式光电编码器可知转子初始位置,但存在成本高、体积大的缺点,在一定程度上限制了其应用[1-7]。
目前,国内对永磁同步电机初始位置检测方法的研究很多,但都有其缺点。基于电机反电势的位置检测方法计算方法简单,但其不足是低速运行或零速时电机反电势较小或为零,从而不利于位置检测或根本无法进行电机初始位置的检测[8]。高频信号注入法解决了反电势法低速运行或零速时的位置检测问题,其高频电流响应信号中含有转子的位置信息,但其对高频电流响应信号的解调算法很复杂,运算量大,理论性强,实际应用往往问题较多[6,7,9-13]。脉冲信号注入法检测转子初始位置方法简单,但检测时间较长,且转子也易受注入脉冲影响而转动[14,15]。
针对以上问题,本文提出一种基于旋转高频信号注入法的永磁同步电机转子初始位置检测方法。通过对三相高频电压信号的电流响应进行低通滤波,得到三相电流响应信号幅值大小关系,再根据三相电流响应幅值大小随转子位置角不同而变化的规律得出转子初始位置信息,最后利用电机磁路饱和效应区分电机转子NS极性。理论分析及实验表明,该方法能准确检测出电机转子初始位置信息,因注入高频电压信号频率高、幅值低,检测过程中电机转子不会发生“抖动”现象,电机起动过程不会出现反转现象,该方法能满足永磁同步电机平稳起动的要求。
1 转子初始位置检测原理
永磁同步电机在静止ABC坐标系中定子电压和磁链方程分别为
(1)
(2)
(3)
式中,ψA、ψB、ψC分别为A、B、C相绕组的全磁链;D代表对时间t的微分;ψfA、ψfB、ψfC分别为永磁励磁磁链过A、B、C三相绕组产生的磁链;ψf为永磁体励磁磁链;θ为d轴和静止三相坐标系A轴的夹角。定子绕组自感、互感分别为
(4)
(5)
式中,LS0为自感系数平均值;LS2为自感系数二次谐波幅值,即LS=LS0+LS2cos(2θ),且有
(6)
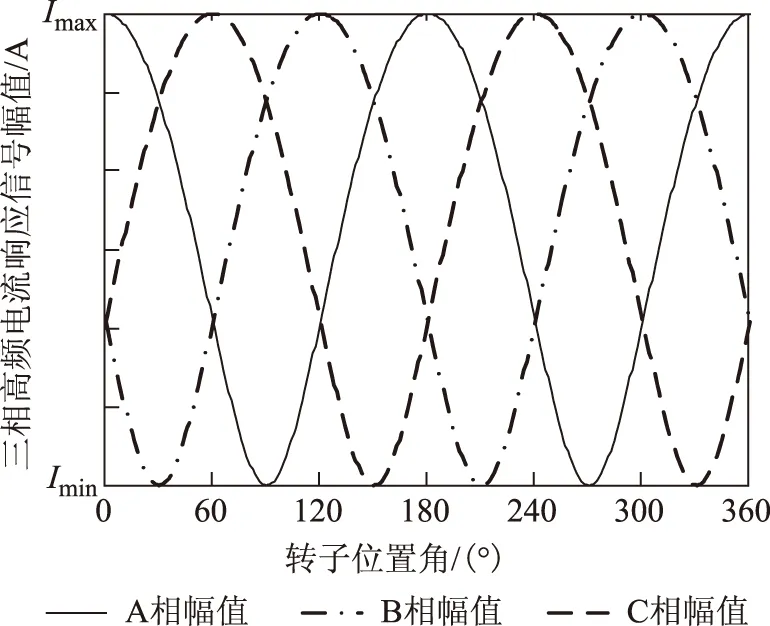
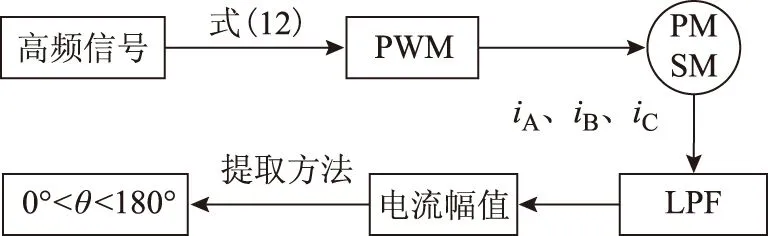
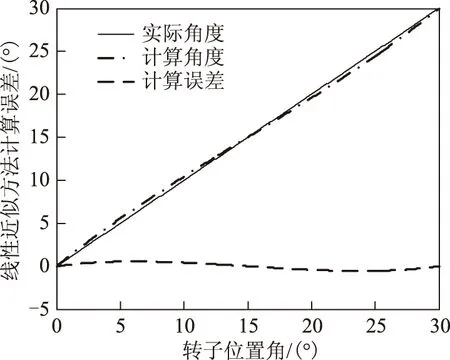
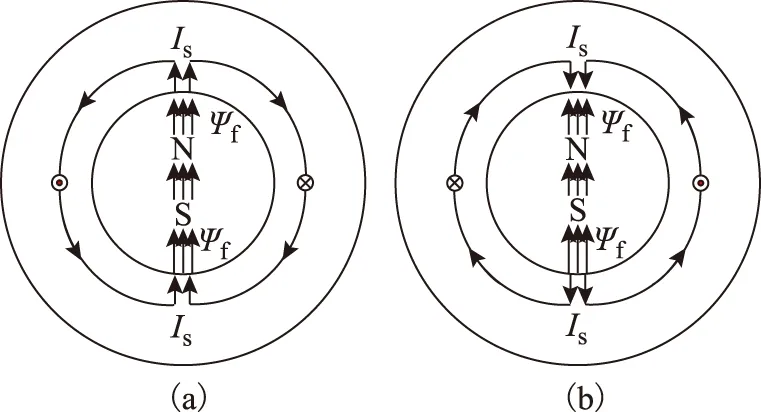
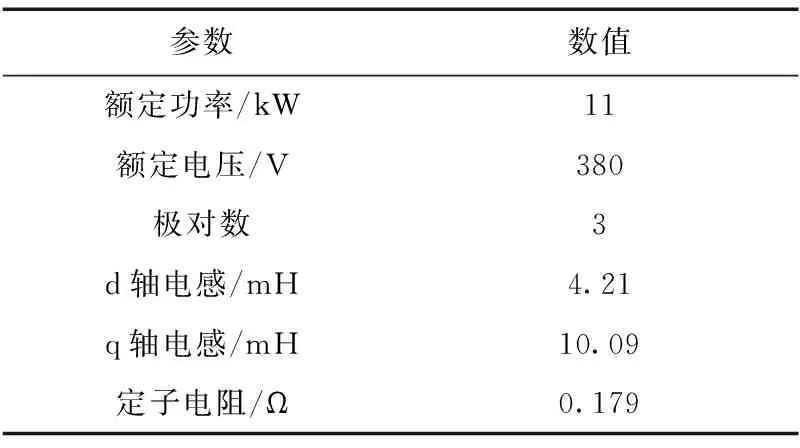
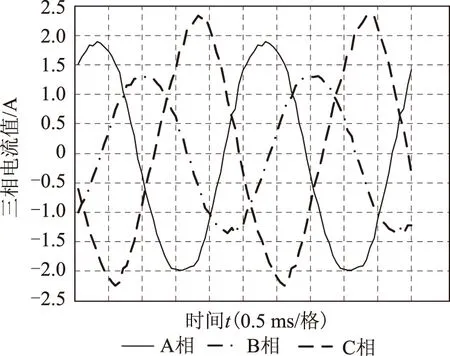
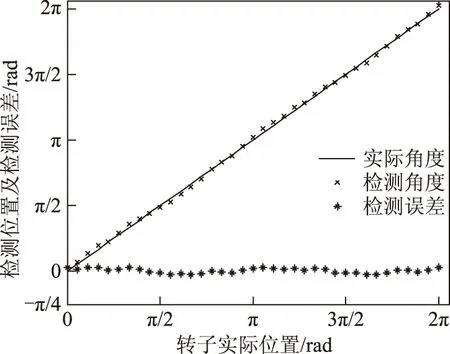
式中,LSd、LSq分别是同步电机直轴、交轴瞬态电感,对于凸极同步电机LSd (7) 将式(3)~式(5)带入式(1)和式(2)中,再通过3/2坐标变换可得永磁同步电机在静止α-β坐标系中定子电压和磁链方程分别为 (8) (9) 式中,ω为转子角速度,ω=dθ/dt, 由于进行初始位置检测时电机静止,令ω=0,由于电机绕组中通入的是高频电压信号,故可忽略定子电阻压降,将式(9)带入式(8)得定子电压方程 (10) 检测转子初始位置需要通过检测定子高频电流响应信号来实现,通过式(10)求得电流响应信号为 (11) 对定子绕组注入持续的高频旋转电压信号,在三相静止坐标系中的电压表达式为 (12) 式中,U为注入高频电压信号的幅值;ωh为注入高频电压信号的角频率。通过3/2变换到两相静止α-β坐标系中 (13) 将式(13)带入式(11)中,经计算可得高频电流响应信号在两相静止α-β坐标系中的表达式为 (14) (15) 可看出A、B、C三相高频电流响应信号均是两个同频率正弦信号的差,由电工基础知识可知两个同频率正弦交流电压之和(差)仍是正弦交流电压,其幅值由两信号各自幅值和两信号的相位差决定。由式(15)和式(7)可知,在电机参数和高频注入信号确定后,θ对三相高频电流响应信号的幅值有调制作用,也就是说θ的不同将导致三相高频电流响应信号幅值的变化,其调制作用如图1所示,表示θ由0°~360°变化时A、B、C三相电流幅值的变化规律。图中幅值大小变化范围(A、B、C三相相同)为 (16) (17) 将图1中三相高频电流响应信号的幅值随θ角的变化规律近似为正弦规律。ΔI由电机凸极性决定,电机凸极性越强(LSq-LSd)越大,因而三相高频电流响应信号幅值变化的幅度ΔI也越大。在后面的分析中可看出,此ΔI值越大越有利于转子位置角θ的提取。从这种规律中提取出θ角信息的过程如图2所示,其中LPF为低通滤波器,提取方法在后文中会进行详细介绍。 图1 θ对三相高频电流响应幅值的调制作用Fig.1 Modulation of θ on three-phase high frequency current amplitude response 图2 θ角提取过程Fig.2 The extraction process of θ 根据图1直接采用查表法提取位置信息会受到注入高频电压信号的幅值U和角频率ωh影响,根据图1中三相电流幅值大小的比例关系提取位置信息则不会受到影响。从图1可看出三相高频电流响应幅值大小随转子位置不同而变化的规律如式(18)所示。 (18) 式中,IA、IB、IC分别为A、B、C三相电流幅值大小,180°<θ<360°的情况与0°<θ<180°的情况相同。通过对三相电流幅值大小进行比较可将θ确定在180°之前的某一个30°范围内(先不对NS极性进行区分,认为0°<θ<180°),根据式(19)的线性近似方法计算θ值。 (19) 图3 线性近似方法计算误差Fig.3 Calculation error of linear approximation 可计算出此误差不超过0.56°(电角度),说明这种数学线性近似方法本身不会带来大的计算误差,这个由计算带来的误差,对永磁同步电机的起动控制,其影响可忽略。 由式(15)可知,尽管各相电流大小及幅值会受到k值的影响,但在式(19)所示的转子位置角θ的提取方法中,k值对各相电流大小及幅值的影响相互抵消,因而,图2所示提取转子位置角θ的过程以及式(18)和式(19)所示的提取方法,不受注入高频电压信号的幅值U和角频率ωh影响,对电机参数不敏感,鲁棒性强。 上节所述提取转子位置角θ的方法,并不能对转子NS极性进行区分,也就是说θ可能对应着N极,也可能对应着S极,而转子NS极性的区分要用到磁路饱和效应。为了充分利用材料,电机再设计时往往要让磁路处于微饱和状态。因此,对电机转子d轴正方向(即N极)施加电压,会使电机d轴磁路过饱和,如图4a所示;对电机转子d轴负方向(即S极)施加电压,会使电机d轴磁路退饱和,如图4b所示。而电机直轴电感LSd会随d轴磁路的过饱和而减小,随d轴磁路的退饱和而增大。 图4 定子磁势对d轴磁路影响Fig.4 Influence of stator magnetomotive force to d-axis flux 由式(14)和式(6)可得电机d轴电流表达式为 (20) 为了验证所提供的永磁同步电机转子初始位置检测方法的正确性,以一台额定功率为11 kW,额定电压为380 V的内嵌式永磁同步电机为研究对象,进行了大量实验。电机参数如表1所示。控制系统以TMS320F2812为核心,主电路采用三相电压源逆变器,向电机注入的高频电压信号幅值大小为80 V,频率为400 Hz。 表1 永磁同步电机主要参数Tab.1 Main parameters of PMSM 图5 θ=0°时的三相高频电流响应波形Fig.5 Three-phase high frequency current amplitude response θ=0° 图6 θ=40°时的三相高频电流响应波形Fig.6 Three-phase high frequency current amplitude response θ=40° 图7 转子位置检测误差Fig.7 Detection error of rotor position 产生误差的主要原因有电流采样误差、系统外部干扰、数学近似模型带来的误差以及电机结构不对称和转子不同位置饱和度不同带来的电流响应误差等。对于各种导致电流检测不准的因素,可采用对三相高频电流响应信号进行低通滤波,滤除杂波信号后再提取电流响应幅值大小的方法。在工程实践中,也可增加注入的高频信号的周期数,从而得到多个周期电流响应信号的幅值,采用平均值法计算电流幅值,从而最大化地减少电流检测不准对线性近似方法的影响。 [1] 刘家曦,李立毅,杜鹏程.考虑磁场交叉耦合的内嵌式永磁同步电机初始位置检测技术[J].电工技术学报,2013,28(7):32-38.LiuJiaxi,LiLiyi,DuPengcheng.Initialrotorpositionestimationconsideringmagneticcross-couplingbasedonIPMSM[J].TransactionsofChinaElectrotechnicalSociety,2013,28(7):32-38. [2] 周元钧,蔡名飞.改进的永磁同步电机转子初始位置检测方法[J].电机与控制学报,2010,14(3):68-72.ZhouYuanjun,CaiMingfei.InitialrotorpositioninspectionofPMSMbasedonrotatinghighfrequencyvoltagesignalinjection[J].ElectricMachinesandControl,2010,14(3):68-72. [3] 金光哲,徐殿国,高强,等.高频注入电压预估同步电机转子位置检测方法[J].中国电机工程学报,2014,34(09):1376-1383.JinGuangzhe,XuDianguo,GaoQiang,etal.Asynchronousmotorrotorpositiondetectionmethodbasedonhigh-frequencyinjectionvoltageprediction[J].ProceedingsoftheCSEE,2014,34(09):1376-1383. [4] 张涛.基于高频信号注入的IPMSM转子初始位置估计[J].硅谷,2009(11):37-38.ZhangTao.InitialrotorpositionestimationbasedonhighfrequencysignalinjectionforIPMSM[J].SiliconValley,2009(11):37-38. [5] 杨立永,陈为奇.永磁同步电机转子初始位置检测研究[J].电气传动,2012,42(3):57-61.YangLiyong,ChenWeiqi.StudyoninitialpositionofPMSMrotor[J].ElectricDrive,2012,42(3):57-61. [6] 唐芬,金新民,周啸,等.一种低成本直驱永磁风力发电机转子初始位置检测方法[J].电气应用,2012,31(16):100-104.TangFen,JinXinmin,ZhouXiao,etal.Alowcostmethodfordirect-drivepermanentmagnetwindturbinerotorinitialpositiondetection[J].ElectrotechnicalApplication,2012,31(16):100-104. [7] 于艳君,柴凤,欧景,等.基于旋转高频信号法的IPMSM无位置传感器控制[J].电工技术学报,2013,28(7):26-31.YuYanjun,ChaiFeng,OuJing,etal.PositionsensorlesscontrolofIPMSMbasedonrotatinghighfrequencysignalmethod[J].TransactionsofChinaElectrotechnicalSociety,2013,28(7):26-31. [8] 李志强,夏长亮,陈炜.基于线反电动势的无刷直流电机无位置传感器控制[J].电工技术学报,2010,25(7):38-44.LiZhiqiang,XiaChangliang,ChenWei.ApositionsensorlesscontrolstrategyforBLDCMbasedonlineBack-EMF[J].TransactionsofChinaElectrotechnicalSociety,2010,25(7):38-44. [9] 刘颖,周波,冯瑛,等.永磁同步电机低速无传感器控制及位置估计误差补偿[J].电工技术学报,2012,27(11):38-45.LiuYing,ZhouBo,FengYing,etal.AnovelsensorlesscontrolmethodofSPMSMatlowspeedandestimatedrotorpositionerrorcompensation[J].TransactionsofChinaElectrotechnicalSociety,2012,27(11):38-45. [10]杨兴华,姜建国.永磁同步电机精确瞬时速度检测[J].电工技术学报,2011,26(4):71-76.YangXinghua,JiangJianguo.Preciseinstantaneousspeeddetectionforpermanentmagnetsynchronousmotors[J].TransactionsofChinaElectrotechnicalSociety,2011,26(4):71-76. [11]HuangZhaobin,YouLinru,WangZhaodong.MotionsimulationandanalysisduringinitialrotorpositionidentificationforPMSMbasedonhighfrequencyvoltageinjection[C].26thChineseControlandDecisionConference,Changsha,2014:1929-1935. [12]王高林,杨荣峰,李刚,等.基于高频信号注入的IPMSM无位置传感器控制策略[J].电工技术学报,2012,27(11):62-68.WangGaolin,YangRongfeng,LiGang,etal.PositionsensorlesscontrolstrategyofIPMSMbasedonhighfrequencysignalinjection[J].TransactionsofChinaElectrotechnicalSociety,2012,27(11):62-68. [13]何栋炜,彭侠夫,蒋学程,等.内置式永磁同步电机转子初始位置估计方法[J].电机与控制学报,2013,17(3):49-55.HeDongwei,PengXiafu,JiangXuecheng,etal.InitialrotorpositionestimationmethodforIPMSM[J].ElectricMachinesandControl,2013,17(3):49-55. [14]陈东升,张淼,张矛盾.基于互感电压的无位置传感器SRM初始位置检测[J].电气传动,2010,40(6):75-77.ChenDongsheng,ZhangMiao,ZhangMaodun.InitialpositiondetectionofsensorlessSRMbaseonmutual—inductancevoltage[J].ElectricDrive,2010,40(6):75-77. [15]林瑶瑶,仲崇权.无传感器永磁同步电机初始位置检测研究[J].电力电子技术,2013,47(10):102-104.LinYaoyao,ZhongChongquan.StudyofinspectionofthesensorlessinitiairotorpositionofPMSM[J].PowerElectronics,2013,47(10):102-104. Estimation of the Initial Rotor Position for Permanent MagnetSynchronous Motors LuJiadongLiuJinglinWeiLichao (School of Automation Northwestern Polytechnical University Xi’an 710129 China) An estimation method for the initial rotor position for permanent magnet (PM) synchronous motor based on the high frequency voltage injection is presented on account of the problems in existing methods,which includes that the rotor may jitter,the methods depend highly on the motor parameters,and the mathematical processing algorithm of the high-frequency current responses during the estimation is complex.In the proposed method,the three phase high frequency voltage signals are laid on the motor first.By comparing the amplitudes of the three-phase high frequency current responses through LPF (low-pass filter),the method obtains the initial rotor position following the rules that the rotor position affects the amplitudes of the three-phase high frequency current responses.Then the motor magnetic saturation effect is used to distinguish the NS poles.The algorithms and the experimental results show that the proposed estimation method for the initial rotor position is correct.And during the estimation,the rotor does not jitter.The method does not need any additional circuits.The mathematical processing algorithm for the high-frequency current response is easy.And the estimation error is small.This estimation method can be used in motor’s smooth start. Permanent magnet synchronous motor,initial rotor position,high frequency signal injection,magnetic saturation effect 陕西省科技统筹创新工程计划(2013KTCQ01-20),航空基金(2013ZC53045)和中央高校基本科研业务费专项资金(3102014JCY01006)资助项目。 2014-11-20 改稿日期2015-01-25 TM315 鲁家栋 男,1990年生,博士研究生,研究方向为运动控制及伺服控制技术。(通信作者) 刘景林 男,1964年生,教授,博士生导师,研究方向为航空航天微特电机及驱动系统、电机智能控制及测试技术等。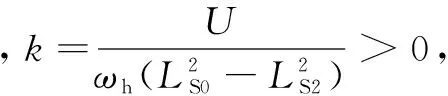
2 转子NS极性判断
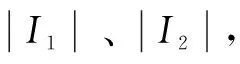
3 实验与结果分析
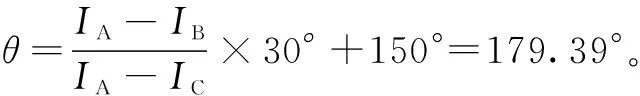


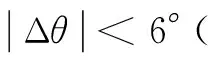
4 结论