2015年广东省中考数学试卷的评析与教学启示
☉广东省东莞市教育局教研室 王健
☉广东省东莞市东莞中学松山湖学校张青云
2015年广东省中考数学试卷的评析与教学启示
☉广东省东莞市教育局教研室 王健
☉广东省东莞市东莞中学松山湖学校张青云
2015年广东省数学中考自问世之日起,就一直为人所热议,在一些微信群或数学QQ群都遭到不少差评或非议.笔者组织了东莞市中考的阅卷工作,对相关的情况有比较多的关注和了解,本文拟以东莞考生的答卷情况为样本,对中考数学试卷作一评析,提出自己的思考,供大家研究参考.
一、考试性质及背景
广东省中考称为“初中毕业生学业考试”,目的是全面、准确地反映初中毕业生的学科学业水平,同时也作为高中阶段学校招生选拔的依据.2015年数学学业考试是采用《义务教育数学课程标准》(2011年版)(以下简称“标准”)和配套课标教材的第一年,要求全面落实课标设立的课程目标,面向全体学生,既重视对学生学习数学知识与技能的结果和过程的评价,也重视对学生在数学思考能力和解决问题能力方面的发展状况及对数学认识水平等方面的评价.试题在除广州、深圳、佛山、珠海、梅州、汕尾等市之外的全省范围内使用,考生人数众多,影响深广.
总体来看,今年的数学中考试题,在保持试卷的结构和难度基本稳定的前提下,重点考查学生核心的数学基础知识和基本技能、基本的数学思想方法及应用数学解决问题的能力等,特别突出强调发展学生的几何直观、运算能力和自主创新意识,强调发展学生的数学思维品质,并尝试在某些方面突破广东省卷历来的命题模式,探索创新.
二、试卷结构分析
1.试卷结构
中考试题题型、分值均和2014年一致,分为选择题10道计30分、填空题6道计24分、解答题(一)3道计18分、解答题(二)3道计21分、解答题(三)3道计27分,全卷共25道120分.选择题是四选一型的单项选择,填空题要求直接填写结果,解答题都应根据题目的要求,写出文字说明、演算步骤或推证过程.
2.试卷知识归类
试卷以《2015年广东省初中毕业生数学学科学业考试大纲》为指导,着重考查“数与代数”“图形与几何”“统计与概率”等核心内容,适当兼顾“综合与实践”领域.具体分布见表1.

表1:试题知识归类表
备注:第10题是函数图像的判断,但根据条件研究中间等边三边形的面积是前提,故划分时,2分归几何、1分归代数;第23题是代数综合题,主体是代数,但第三问包含有最短路径问题,评分标准1分归几何;第25题是代数几何综合题,但主体是几何知识,仅在第三问中有求二次函数解析式的最大值,评分标准1分归代数.
由表1可以看到,2015年广东数学试卷基本覆盖到了“标准”相关部分规定的课程内容,实现了考试预定的“以‘标准’中的‘课程内容’为基本依据,不拓展知识与技能的考试范围,不提高考试要求,选学内容不列入考试范围”的考试目标,但同时我们也看到,“数与代数”“图形与几何”内容比例分配上出现了前者反而更少的倒挂,这与考试大纲的规定有一定的出入,和人教版教材对应知识的教学课时比也不相符.
3.试卷对思想方法及能力的考查情况
试卷在考查学生核心的数学基本技能、基本的数学思想方法及应用数学解决问题的能力方面的情况见表2.
变频调速器的价格相对于电动机来说是比较贵的,因此在保持安全可靠运行的前提F,合理地降低变频调速器的容量.对节省费用是很必要的。一般变频调速器生产厂家要求选用变频器功率应大于或等于电动机额定功率的1.1倍。从设计角度结合文践中测得的自关数据显不,这一规定不符合石化企、IP的具体情况,留有的余量太大。

表2:试卷考查数学思想方法及能力分布表
与原实验版课标不同,在“标准”中特别提到了十个关键词:数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识,其中“几何直观、运算能力、模型思想、创新意识”为新增.从表2可以看出,作为使用“标准”为依据的第一年中考,试卷对新动向有着非常清晰的回应.与此同时,我们没有看到与视图和分类讨论思想相关的设计.
4.学生答卷情况
东莞近年来教育教学质量逐年提高,中、高考成绩在广东全省范围内均处于较高的水平.今年数学中考,东莞全市41633人,平均分86.77,有19241人分数≥96,优秀率46.21%,有33722人分数≥72,合格率81%,各项指标均位居全省第一.
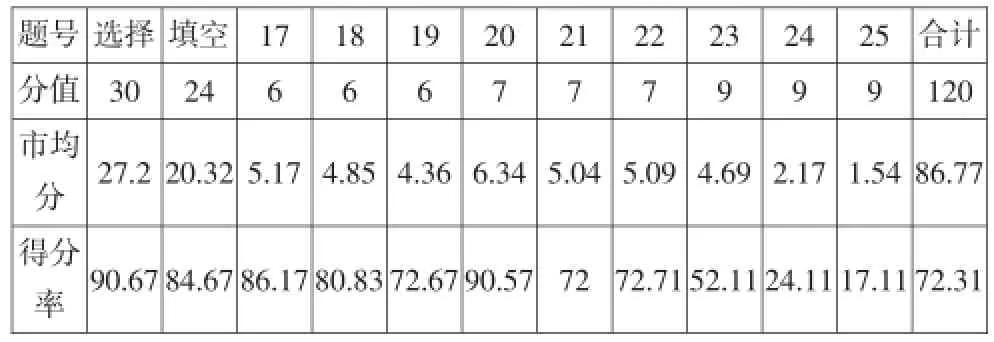
表3:东莞考生答题得分情况表
按难易程度,试题分为基础题(得分率在80%以上)、中档题(得分率在40%~80%)和较难题(得分率在40%以下).从学生的得分情况来看,基础题计73分,中档题计29分,较难题计18分,各部分所占比例分别为60%、25%、15%,基本达成中考大纲预定目标.市均分与2014年市平均分90.6纵向比较,表明试卷整体难度较2014年有所上升.
三、试卷特点及教学启示
1.注重基础是永远的基调
今年的试卷虽然饱受诟病,以至一些微信圈都爆出了“广东十年来最难中考”的议论,但后来人们对照市均分,发现其实结果并没有想象中的那样糟糕.究其原因,与试卷中仍然坚持以基本知识和基本技能为考查主基调是分不开的.注重“双基”,在任何时候都是数学中考命题的第一原则.从上面东莞考生各题的得分率来看,整个试卷在个别试题较难的情况之下,仍然保证基础试题占到全卷的六成,像选择题1~8、填空题11~15、解答题(一)(二)等,都是源于教材,立足基础,这就保证了绝大多数考生都能够得到基础分.
教学启示:在教学或中考复习过程中,我们还是要坚持注重“双基”,突出主干知识的落实,强化对基本概念、定义、法则、定理的理解和运用,培养学生严谨审题和规范性答题的思维习惯.比如,试题“11.正五边形的外角和等于______(度)”,批阅中发现就有不少学生误答为内角和“540°”;试题“17.解方程:x2-3x+2=0”,有近四成的考生出现选择方法不够简洁、步骤表达不规范、求根公式记错、配方出错、开方漏根等失误;试题20是画树状图求随机事件的概率,发现有不少学生没有任何步骤直接作答,或者对树状图的意义理解不深刻,出现“会画不会求”等,这些表现都告诉我们,教学要咬住“双基”不放松.
2.回应新“标准”
教学启示:教师要加强学习,深刻理解把握新“标准”的理念和目标,并将这种新变化、新理念贯穿在自己的教学过程中,要重视对基本思想、方法的归纳、理解和运用,创造条件让学生参与数学学习的全过程,促进他们基本活动经验的积累与丰富.同时,要重视诸如几何直观、运算能力、模型思想、创新意识等新领域、新要求的教学,有意识地训练学生思维的灵活性与开放性,在提升思维品质上下功夫.
3.加强创新求变
广东省的数学中考近几年来一直在探索着更完美的试卷结构,今年的试卷在保持总体结构不变的情况下,加强了对传统固有定式突破的举措,比如对解直角三角形的考查形式,以前多数都是以一道解直角三角形的实际应用展开的,但今年却将此知识点的考查散落在题19、题25之中,将应用化作一种方法包容在解决问题的过程之中,这既体现了重点考查学生运用数学知识分析问题和解决问题的能力,发展他们基本活动经验的命题理念,也使命题呈现出一定的多样性,使中考猜想不至于成为一场教师和学生都认为是“铁板钉钉”的游戏.再比如,试卷中缺失了对三视图和分类讨论数学思想的考查,虽然我们对这一点持保留意见,但在没有偏离“核心概念、思想方法和常用的技能”情况下,个别内容的缺失也未尝不是不可以的事.
教学启示:从创新的角度,套用一句话:没有什么不可以改变.在教学过程中,一方面,我们要踏踏实实,抓住主线,立足数学本质进行教学,以“不变应万变”;另一方面,我们要在学习过程中,大力鼓励并发展学生的发散思维,培植他们的反思与辩驳能力,提高他们的创新意识.同时,我们也要注意,不可过于功利化,以考定教,考什么才教什么,或者听凭想象与经验投机,靠猜题、押题应对.
四、几点商榷
1.重复考查是突出重点吗
仔细分析试卷,我们发现,试卷中有多题似乎陷入了知识点重复考查的疑团之中.
题1:(3分)|-2|=().
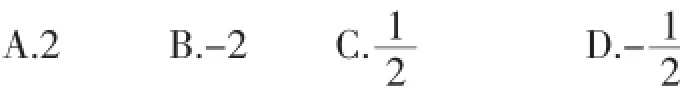
题7:(3分)在0、2、(-3)0、-5这四个数中,最大的数是().
A.0B.2C.(-3)0D.-5
评析:题1求有理数的绝对值,题7考查零指数幂,并比较有理数的大小,虽然是从不同角度来考查,但两题从本质上都可归于实数,而且都过于简单.研究其他省市的中考题,不难发现有一些地区是以类似于题7的试题作为试卷开篇第一题的,所以我们以为:题7要么不该出现,要么就是放置的位置不对.

评析:这两题是从不同的角度来考查学生对于分式的学习情况.题13要求会解可化为一元一次方程的分式方程,题18要求会利用分式的基本性质进行约分和通分,进行简单的分式加、减、乘、除运算.两题合计10分,这在中考卷中是不太多见的设计.分式具有综合性,其计算要应用到整式运算,分式方程也要运用到解整式方程,是中考的必考内容之一,但有必要在同一份卷中既有分式的化简求值,又有解分式方程(应用题)吗?这个问题值得斟酌,从知识覆盖面上讲,我们更主张回避,二者有其一即可.
类似的还有题17、题21、题23都涉及解一元二次方程,题22、题23都涉及解二元一次方程组,题23、题25都涉及较为复杂的二次根式分母有理化等.诚然,知识彼此之间是相互联系的,有一些知识的确具有较强的综合性,但中考试卷毕竟不是单元检测,在中考涉及的“标准”155个知识内容条目中,一份中考试卷大约只能覆盖到其中的40个左右,所以每个题每个知识点之间搭配要科学合理,平衡恰当.这种对局部知识的重复考查让人感觉有命题浪费之疑.
2.加强运算并不是重陷繁难
“代数学的根源在于代数运算”.新“标准”指出:“运算能力主要是指能够根据法则和运算律正确地进行运算的能力.培养运算能力有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题.”但加强运算能力,并不是要重走以前那种繁、难、杂的传统笔算之路,相反地,要大大降低运算的难度和复杂程度,使学生从大量的机械计算中解脱出来,把更多的时间和精力转向追求理解算理,根据问题寻求最优运算途径之上.在本卷中,如果题23中需要运用到的形化简还可以接受的话,那么对于题25中,需要多次反复用到的相关式子的计算,的确就是为难学生了,这也就是为什么全市四万多人结果仅有39人获得小胜(9分题获得8分)的原因.结果运算正确似乎变成了一个像体彩获奖一样的小概率事件.
3.压轴设置并不是“堵死”学生
出于选拔性考试需要,在试卷中设置有一定难度的压轴题当然是必须的,但难度究竟要控制到什么程度呢?像本试卷题25(3)中,需要针对所求得的二次函数解析式研究其最大值,从知识内容上说,这个应当不难,但问题在于这个来之不易的解析式本论是采用公式法还是配方法,其计算量都甚于“登天”.笔者询问老师们:你做出最后结论了吗?结果没有一个老师有耐心地做出结果.连在下面从容做的老师都如此,更何况还是身处考场的学生乎!不仅东莞全市本题无一人得满分,而且据了解,全省其他地市也是如此.压轴题考验学生的综合能力,的确不是所有学生都能解决的,但压轴并不是要“堵死”学生,无论怎么“压”,命题都要给部分学生留下一条通往顶峰的小径,让他们有机会问鼎,有可能登峰.
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
2.项武义.基础代数学[M].北京:人民教育出版社,2004.
3.张青云.运动之中的常规考量——2014年广东卷中考第25题的思路突破与教学建议[J].中学数学(下),2015(1).
4.庞彦福,姜鸿雁.立足主干,体现基础,关注能力——2015年安徽省中考数学试卷评析及教学启示[J].中学数学(下),2015(9).
5.张青云,刘翥远.2015年广东卷第20题阅卷报告——解答题答题失误现象分析[J].中学数学教学参考(中),2015(10).Z

