基于逆向游走的PageRank社交网络影响力度量算法＊

郑孝遥，杨文建，鲍 煜，罗永龙

（安徽师范大学数学计算机科学学院，安徽 芜湖241003）

1 引言

以用户为中心的社交网络已成为互联网的一大发展趋势，并成为人们分享、获取和传播信息的重要渠道。社交网络是以计算机网络为基础，建立一个人与人之间相互了解的网络结构［1］。社交网络中的节点影响力一直是一个重要的研究内容，其在社会舆论传播和导向、群体行为形成和发展等方面都具有重要作用［2］。随着社交网络中用户规模呈指数级增长，节点影响力度量的精确性和计算效率成为一个关键问题［3，4］。

目前，国内外对社交网络中节点影响力度量方法的研究主要有三种［5～7］：

（1）基于节点度的度量方法。在该类方法中，以节点的度作为评判标准，对节点影响力进行量化，但其只考虑了邻居节点对当前节点影响力的贡献，忽略了节点影响力传播路径上其它节点对其的影响，导致影响力度量不够准确［8］。

（2）基于最短路径的度量方法。该方法主要包括紧密中心度和介数中心度两种度量方法［9］。紧密中心度考虑了节点消息传播的速度，节点传播速度越快，节点影响力越高。介数中心度考虑了节点在网络中所处位置的重要性，认为节点位置越重要，消息通过其的概率越高，其影响力越大。但是，由于该类方法均需要花费最低O（cne）（n＝|V|，e＝|E|，c是趋近于2的常数）的时间计算最短路径，因此时间效率太低。

（3）基于随机游走的度量方法，包括特征向量中心度、Katz中心度、PageRank等［10］。特征向量中心度考虑邻接节点影响力，将邻接节点影响力的线性和作为当前节点影响力判定的依据。Katz中心度考虑当前节点的随机游走路径，依据随机游走路径上的节点影响力加以惩罚得出当前节点影响力。PageRank算法考虑节点的数量和质量，每个节点的影响力均在网络中均匀流动，最终以迭代收敛值作为节点的影响力权值，但当节点较多时迭代计算代价较高。

传统的社交网络影响力度量方法由于计算复杂度高，已不能适应当前社交网络的发展需求，随着大数据技术的发展，如何在海量的社交网络数据中快速准确地计算和分析出用户节点的影响力是一个亟待解决的研究课题。

针对上述三种主要方法中存在的度量不准确、计算复杂度高等问题，本文提出一种基于随机游走的分布式PageRank算法，本文称为Reverse PageRank。经过在公开数据集的实验仿真，验证了该算法在迭代次数较少时具有较好的精确度和时间性能。

2 相关研究

由于PageRank算法能够较准确地度量社交网络节点的全局影响力，因此基于PageRank的影响力度量方法越来越受重视。本节主要介绍两种典型的随机游走PageRank算法：传统的随机游走算法［11］和Fast PageRank算法［5］。

2.1 传统随机游走PageRank算法

考虑用户在浏览网页时，会以某个概率1－ε（ε＝0.15）沿着网页中的链接访问网页，以ε的概率随机选取一个网页访问（由于用户会以ε的概率随机选取一个网页访问，因此本文将其称为跳转因子）。

传统随机游走PageRank 算法正是基于上述思想，模拟上述过程，实现了传统迭代式PageRank算法的分布式计算。令n为节点数目，e为边数，K为模拟次数总数与e的比值，ε为跳转因子，为vi的PageRank值。算法首先初始化然后循环Ke次，对于每次循环，随机选取节点vi，重复下列操作：对vi以1－ε的概率随机选取后继节点vj，以ε的概率重新选取新节点赋给vi，对于第一种情况，加1，将vj赋给vi，对于第二种情况，跳出重复。模拟结束后，得出的即为PageRank值，按其值排序即可得到影响力排名。

传统随机游走PageRank 算法实现了传统迭代式PageRank算法的分布式计算，但由于其每一步均具有很强的随机性，运算结果与传统迭代式PageRank算法会有较大偏差［12，13］。

2.2 Fast PageRank算法

Fast PageRank算法最早是由Sarma A D 于2013年提出的，其思想是将传统随机游走PageRank产生的链路分割，仅考虑当前以及随机产生的下一个节点，在每次循环时对所有节点模拟单步随机游走，即该算法在单次循环可分布式。该算法每次循环结束时均需要修改下次循环每个节点的模拟次数，从而利用上次计算结果为节点的PageRank值计算提供修正，提高了计算精确性。

令n为节点数目，e为边数，ε为跳转因子，单个节点的随机游走次数初始值K＝clogn，其中（δ为任意常数，t为调整系数，W为随机变量），为节点vi的随机游走次数，为节点vi的影响力值，为当前循环中随机游走经过边（vi，vj）的次数。算法首先初始化然后循环Blogn/ε（B是一个充分大的数）次。对于每一次循环，首先初始化然后于对每每次个模节拟点，重复次模拟。对于每次模拟，以1－ε的概率随机选取vi的后继节点vj，以ε的概率重新选取新节点赋给vi，对于第一种情况，加1。每次循环所有节点模拟结束后，计算外层循环结束后得出的即为PageRank值，按其值排序即可得到影响力排名。

Fast PageRank算法每次修改模拟次数时需要将所有节点集中，即使其在每次循环时对节点并行处理，其在进行模拟次数修改时也需要大量计算机间的通信，时间效率较低。

本文基于逆向查找访问消息传播路径的思想，给出一种改进的随机游走PageRank算法。

3 Reverse PageRank

3.1 算法思想

本文将社交网络中的用户抽象成节点，用户之间的访问抽象成边，则社交网络可用有向图D ＝（V，E）表示，其中V 是节点集合，V ＝｛v1，v2，…，vn｝；E 是所有节点间有向边的集合。假设节点vi访问了节点vj，则节点vi和节点vj之间存在一条有向边eij（eij∈E）。

则算法思想可抽象为：

Step 1 对于每个eij∈E；

Step 2 如果transmit （vj，vk）返回true，转step 3；否则，转step 4；

Step 3 对vj、vk必存在ejk∈E，将vi⇐vj，vj⇐vk，转step 2；

Step 4 对于eij，可以得到消息逆向传播路径vi→vj→vk→… →vx ，其中认为vx为消息原创者，则消息的传播路径为vx→…→vk→vj→vi。本模型认为，vi访问vj这个行为，向此路径上除vi外的其他节点反馈了影响力，此影响力在本模型中被数值化为1。

其中，transmit （vj，vk）所实现 的功能 为若vj为消息传播源，则不需要继续查找消息传播源，返回false；反之，则继续查找消息传播源，将下一步随机游走节点保存在vk中，返回true，具体实现见算法1。

算法1 函数transmit（vi，vj）

本文基于用户之间的消息传播，采用逆向查找消息原创者的思想找到消息的一条传播路径，当然此路径具有很强的随机性。本文采用多次模拟的思想将其优化，使结果更准确。

3.2 算法实现

3.1节叙述了算法思想，将此思想进一步形式化，即可得到算法，本文将其称为Reverse PageRank，如算法2所示。

算法2 Reverse PageRank 算法

输入：节点的个数n，每条边模拟随机游走次数K，跳转因子ε；

输出：每个节点的影响力值。

算法步骤：

从本质上看，本文算法是一个随机游走算法，与传统随机游走PageRank 算法很类似。二者之间不同的是，传统随机游走PageRank算法每一步的选择均是随机的，而Reverse PageRank 对有向图中每条边进行随机游走模拟，即将原本对每条边分布不均匀的模拟次数均匀地分配给每条边，真实反映消息在社交网络中传播的路径。另外，与Fast PageRank相比，Reverse PageRank以深度优先搜索消息逆向传播路径为主要思想；而Fast PageRank是对整个社交网络中所有节点均进行一次随机游走后才开始下一次随机游走，且后一次随机游走是以前一次随机游走为基础，是一种广度优先的随机游走。

4 仿真实验

4.1 实验数据及评价

本文仿真实验分别选取了三种不同数量级的数据集来分别测试，其中数据集1、3来源于斯坦福大学的大规模网络数据集［16］。数据集1是一个技术新闻类用户社区数据；数据集2为真实的博客用户访问数据，来源于文献［17］；数据集3是斯洛伐克的一个在线社交网络数据集。表1中给出了具体的数据规模。

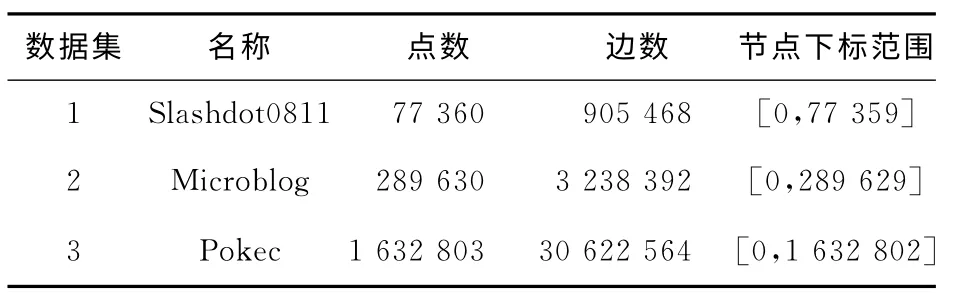
Table 1 Test datasets表1 测试数据集

本文首先将表1中的数据用传统迭代式PageRank算法计算出每个节点的真实PageRank值，并将其作为节点在社交网络中影响力的参考基准。其次是分别运行传统随机游走PageRank 算法、Fast PageRank 算 法 以 及 本 文 的Reverse PageRank算法得出其节点影响力排名。最后将三种对比算法得到的影响力排名与基准排名进行比对，测算出对比算法排名的准确性，本文用趋近度来表示准确性。趋近度定义为：

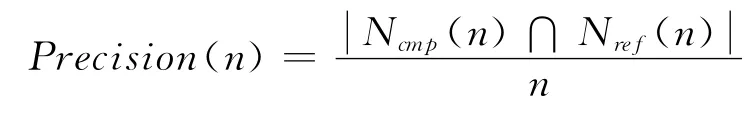
其中n表示社交网络节点影响力排名的前n个节点；Nref（n）表示真实社交网络影响力排名前n个节点所组成的集合，本文用传统迭代式PageRank作为基准；Ncmp（n）表示比较算法社交网络影响力排名前n个节点所组成的集合。

根据趋近度的定义，当n从1开始变化时可形成一条趋近度的曲线，本文以该曲线作为算法准确性的评判标准。比较算法得出排名与传统迭代式PageRank算法趋近度越高，相应曲线越趋近于上界1，表明算法的准确性越好。

4.2 实验结果及分析

为了比较公平性，本文只对随机游走参数K（K代表模拟的游走次数）和跳转因子ε进行设置，并比较在不同参数设置下传统随机游走算法（RandomPR）［11］、Fast PageRank（FastPR）［5］和本文中的Reverse PageRank（ReversePR）的趋近度。图1～图3中分别给出了三个数据集在游走参数K＝｛1，5，10，20，50｝情况下，阻尼系数ε在［0.1，0.9］的趋近度。由于篇幅限制，本文只给出了三种阻尼系数ε的实验结果图，分别是0.1、0.9 和FastPR 与ReversePR 的性能临界时的ε的值。

从图1～图3中可以看出：

（1）在K、ε取任意值时，ReversePageRank均比传统随机游走PageRank算法更靠近上界1。因此，Reverse PageRank算法明显优于传统随机游走RandomPR 算法。

（2）Reverse PageRank 在ε取 值［0.4，0.90］时，比Fast PageRank 算法更靠近上界1，即当模拟次数较少、跳转因子较大时，Reverse PageRank优于Fast PageRank算法。

（3）随着社交网络中节点和边的数量增加，Reverse PageRank相对Fast PageRank算法的优势逐渐增大。

通过实验分析，可得Reverse PageRank 算法优于传统随机游走PageRank 算法，并且当K较小、ε较大时，Reverse PageRank优于Fast PageRank算法。当K较大时，Fast PageRank 比Reverse PageRank更趋近传统迭代式PageRank，但Fast PageRank每次迭代都需要计算所有节点的下一次模拟次数，因此当社交网络节点数量较大时，其算法时间性能将急剧下降。而本文提出的算法在K较小、ε较大时即与传统迭代式PageRank算法有更好的趋近度。通过三个不同数量级上的实验对比分析，本文提出的Reverse PageRank 在兼顾计算时间和效率的情况下可以在K在［1，20］、ε在［0.4，0.9］时获得一个较优的度量值。因此，Reverse PageRank 算法在社交网络节点数目较大时具有较强的适用性。

从第4节的仿真实验可以看出，Reverse PageRank相对于传统随机游走PageRank 可以更好地与传统迭代式PageRank 趋近，同时与Fast PageRank相比，本文提出的Reverse PageRank算法在迭代次数较少的情况下，跳转因子ε较大时，精度明显优于Fast PageRank。这是因为在真实社交网络中，大部分消息都是以较低概率向邻居节点传播，只有少部分消息以较大的概率向周围节点传播［15］，因此跳转因子值较大时模拟出的随机游走能比较恰当地反映真实社交网络中的消息传播，也一定程度上体现了本文算法设计的合理性。

5 结束语

本文提出的Reverse PageRank算法是基于逆向查找消息传播源的思想，提出了一种改进的随机游走PageRank算法。实验表明，该算法在模拟次数较少、跳转因子较大时相对传统随机游走PageRank算法以及Fast PageRank算法准确度更高，当社交网络较大时，利用其做影响力度量将比其他两种算法更有优势。

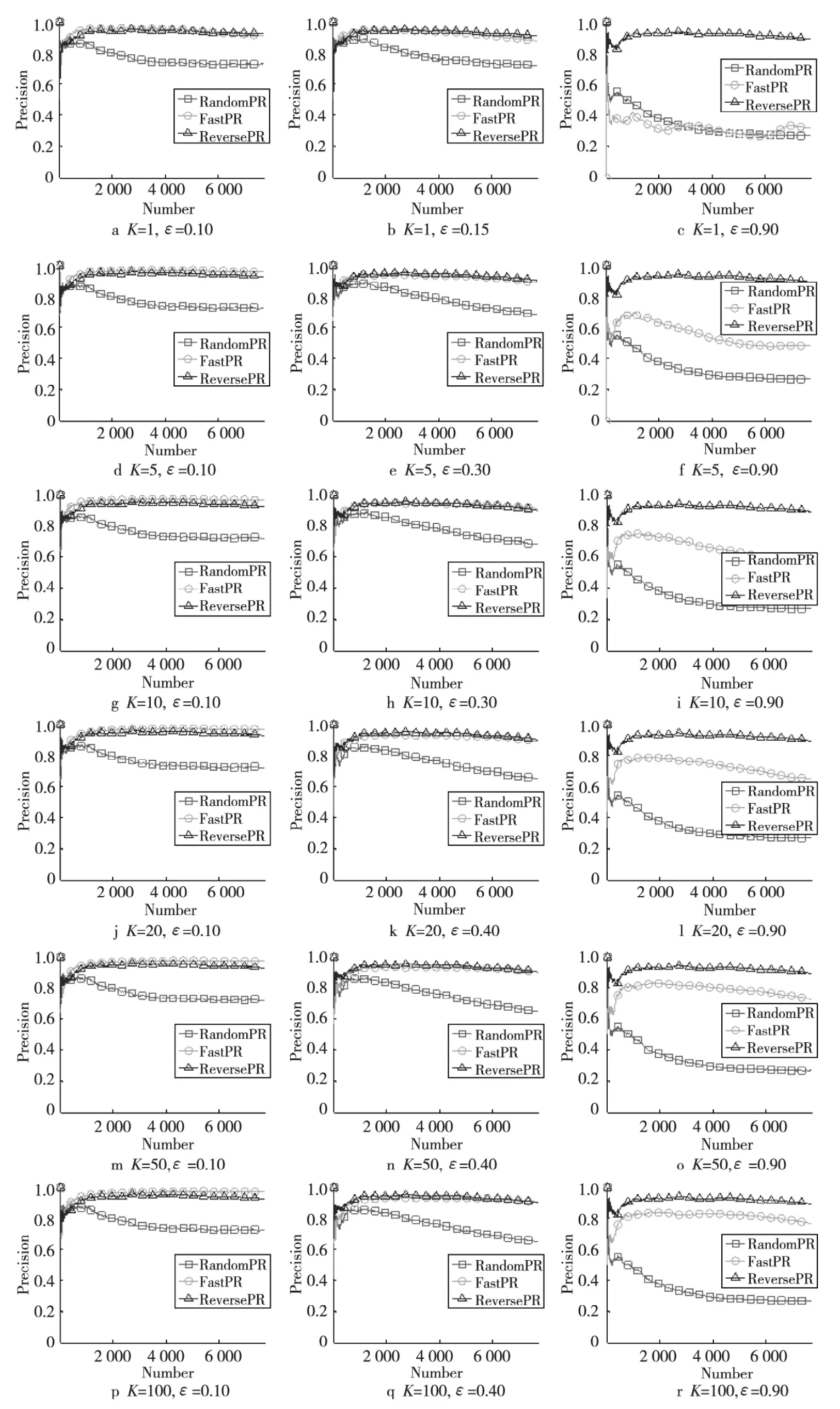
Figure 1 Simulation experiments on Slashdot0811dataset（V ＝77 360，E ＝905 468）图1 Slashdot0811数据集仿真实验（V ＝77 360，E ＝905 468）

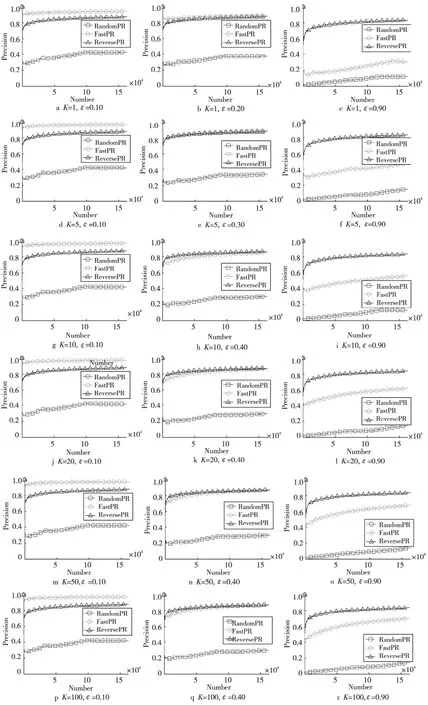
Figure 3 Simulation experiments on Pokec dataset（V ＝1 632 803，E ＝30 622 564）图3 Pokec数据集仿真实验（V ＝1 632 803，E ＝30 622 564）

［1］ Wu Xin－dong，Li Yi，Li Lei.Influence analysis of online social networks［J］.Chinese Journal of Computers，2014，37（4）：735－752.（in Chinese）

［2］ Zhao Zhi－ying，Yu Hai，Zhu Zhi－Liang，et al.Identifying influential spreaders based on network community structure［J］.Chinese Journal of Computer，2014，37（4）：753－766.（in Chinese）

［3］ Liu Zhi－peng，Pi De－chang.Mining social influence of nodes from mobile datasets［J］.Journal of Computer Research and Development，2013，50（Suppl.）：244－248.（in Chinese）

［4］ Chen Hao，Wang Yi－tong.Threshold－based heuristic algorithm for influence maximization［J］.Journal of Computer Research and Development，2012，49（10）：2181－2188.（in Chinese）

［5］ Das Sarma A，Molla A R，Pandurangan G，et al.Fast distributed PageRank computation［J］.Theoretical Computer Science，2015，56（10）：113－121.

［6］ Ding Zhao－yun，Jia Yan，Zhou Bin，et al.Survey of influence analysis for social networks［J］.Computer Science，2014，41（1）：48－53.（in Chinese）

［7］ Liu Yan－heng，Li Fei－peng，Sun Xin，et al.Social network model based on the transmission of information［J］.Journal of Communications，2013，34（4）：1－9.（in Chinese）

［8］ Zhao W，Chen H F，Fang H T.Convergence of distributed randomized PageRank algorithms［J］.IEEE Transactions on Automatic Control，2013，58（12）：3255－3259.

［9］ Ding Z，Jia Y，Zhou B，et al.Mining topical influencers based on the multi－relational network in micro－blogging sites［J］.China Communications，2013，10（1）：93－104.

［10］ Sarma A D，Nanongkai D，Pandurangan G，et al.Distributed random walks［J］.Journal of the ACM （JACM），2013，60（1）：1－31.

［11］ Page L，Brin S，Motwani R，et al.The PageRank citation ranking：bringing order to the Web［J］.Stanford Infolab，1999，9（1）：1－14.

［12］ Henzinger M R，Heydon A，Mitzenmacher M，et al.Measuring index quality using random walks on the Web［J］.Computer Networks，1999，31（11－16）：1291－1303.

［13］ Li L，Xu G，Zhang Y，et al.Random walk based rank aggregation to improving web search.［J］.Knowledge Based Systems，2011，24（7）：943－951.

［14］ Lee S，Jin H L，Lim J，et al.Robust stereo matching using adaptive random walk with restart algorithm［J］.Image and Vision Computing，2015，37：1－11.

［15］ Csáji B C，Jungers R M，Blondel V D.PageRank optimization by edge selection［J］.Discrete Applied Mathematics，2014，169（6）：73－87.

［16］ https：//snap.stanford.edu/data/index.html.

［17］ Zhong E，Fan W，Wang J，et al.ComSoc：adaptive transfer of user behaviors over composite social network［C］∥Proc of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2012：696－704.

附中文参考文献：

［1］ 吴信东，李毅，李磊.在线社交网络影响力分析［J］.计算机学报，2014，37（4）：735－752.

［2］ 赵之滢，于海，朱志良，等.基于网络社团结构的节点传播影响力分析［J］.计算机学报，2014，37（4）：753－766.

［3］ 刘志鹏，皮德常.从移动数据中挖掘网络节点的影响力［J］.计算机研究与发展，2013，50（Suppl）：244－248.

［4］ 陈浩，王轶彤.基于阈值的社交网络影响力最大化算法［J］.计算机研究与发展，2012，49（10）：2181－2188.

［6］ 丁兆云，贾焰，周斌，等.社交网络影响力研究综述［J］.计算机科学，2014，41（1）：48－53.

［7］ 刘衍珩，李飞鹏，孙鑫，等.基于信息传播的社交网络拓扑模型［J］.通信学报，2013，34（4）：1－9.