具有7－（8，0）型自同构的二元双偶极值码＊

王 荣，王俊新

（山西财经大学应用数学学院，山西 太原030006）

1 引言

无线数据传输是当今通信领域中最为活跃的研究热点之一［1］，随着其蓬勃发展，对编码纠错的精确位数和程度要求越来越高。自对偶编码在编码纠错中起着重要的作用。所有长度不超过32的自对偶编码的生成矩阵及其分类已全部解决［2，3］。对长度大于32的编码虽已有很多研究，但找出其生成矩阵和分类情况仍是很困难的。2012 年，Bouyuklieva S［4］对二元自对偶编码［48，24，10］进行讨论，得到在等价情况下，共有264种3－（16，0）型的编码。同年，Aguilar－Melchor C、Gaborit P和Kim J－L［5］证明了存在2 744种［38，19，8］，极值码，两个s－极值码。2011年，Yorgov V［6，7］证明了对于有7阶自同构的二元极值码［42，21，8］，在等价情况下只有29种。2005年，Bouyuklieva S、Yankov N 和Russeva R［8］证 明 了 有3 阶 自 同 构 的 二 元 自对偶码［42，21，8］恰 好 有16 607 种。2005 年，Goodwin V 和Yorgov V［9］证明了至少存在70种长度为88的双偶极值码。本文对码长为50到70之间的二元双偶极值码进行研究。

2 基本知识

二元的［n，k］编码C是指二元域GF（2n）上的k维线性子空间，n称为编码的码长。C的每个元素称为一个码字。对编码C的每一个码字u＝（u1，u2，…，un），其重量wt（u）是u的非零位的位数。两个 码 字u＝（u1，u2，…，un）和v＝（v1，v2，…，vn）的距离指它们在对应位取值不同的位数，用dis（u，v）表示，dis（u，v）＝wt（u－v）。最小距离为d的［n，k］编码称为［n，k，d］编码。对一个编码C，令C⊥＝｛v｜（u，v）＝0，∀u∈C｝（（u，v）为GF（2n）上的内积），如果C＝C⊥，则C在该内积下自对偶。

对［n＝2k，k，d］二元自对偶码，若其码字的重量都是4的倍数，则称该编码是双偶编码。对一个长度为n的双偶编码的距离d≤4［n/24］＋4，若等号成立，编码是极值码［10］。∀σ∈Sn（Sn为n阶对称群），∀u∈C，定义uσ＝（uσ（1），uσ（2），…，uσ（n）），则Cσ和C是等价的。如果Cσ＝C，σ就是编码C的一个自同构，C的所有自同构形成了Sn的一个子群，称之为C的自同构群，用AUT（C）表示。设置换σ∈AUT（C），若σ的阶为奇素数p，有c个独立的循环和f个固定点，则这个置换具有型p－（c，f）。

引理1［11］C是有型p－（c，f）的自对偶编码［n，n/2，d］，p是一个奇素数，定义g（k）＝d＋d/2＋…＋d/2k－1，则：

（1）pc≥g（（p－1）c/2），如果d≤2［（p－1）c/2］－2，等号不满足；

（2）若f＞c，则f＞g（（f－c）/2），若d≤2［（f－c）/2］－2，等号不满足。

对长度为56 的二元双偶码讨论，得到p－（c，f）只有以下几种可能：3－（18，2），3－（16，8），3－（14，14），5－（10，6），7－（8，0），7－（7，7），13－（4，4）。本文考虑有型为7－（8，0）的二元双偶极值码。

3 码的构造

对长度为56的编码，当具有型7－（8，0）时，自同构形式为：

σ＝（1，2，…，7）（8，9，…，14）…（50，51，…，56）

令Ω1＝（1，2，…，7），Ω2＝（8，9，…，14），Ω8＝（50，51，…，56）。

令F（σ）＝｛u∈C｜uσ＝u｝，对∀u∈F（σ），s，l∈Ωi，1≤i≤8，有us＝ul。定义映射（ηu）i＝uj，j∈Ωi，i＝1，2，…，8。把η（F（σ））称为由C导出的收缩码。显然F（σ）由收缩码η（F（σ））唯一确定。

令R＝GF（2）［x］/〈x7＋1〉，x是 不 定 元，〈x7＋1〉是x7＋1 生成的理想。x7＋1＝h0（x）h1（x）h2（x），其中，h0（x）＝x＋1，h1（x）＝x3＋x2＋1，h2（x）＝x3＋x＋1。令Ij＝〈（x7＋1）/hj（x）〉，j＝0，1，2，则R＝I0⊕I1⊕I2。

对长度为7 的向量（a0，a1，…，a6），可看成R上的多项式a0＋a1x＋…＋a6x6［12］。设P是R上偶重量多项式的集合，则P＝I1⊕I2，且I1≅I2≅GF（23）。把I1和I2看成长度为7的编码，表1给出I0、I1和I2的元素，α和γ是I1和I2的本原元。

Table 1 Elements of I0，I1and I2表1 I0、I1 和I2 的元素

令Ei（σ）＝｛u∈C｜且有u｜Ωj∈Ii，1≤j≤8｝，i＝1，2。根据文献［11］得C＝F（σ）⊕E1（σ）⊕E2（σ）。对编码C的每个元素u＝u1u2…u56，定义j＝1，2，…，8；Ei（σ）＊＝｛u＊｜u∈Ei（σ）｝，i＝1，2。令E（σ）＊＝E1（σ）＊⊕E2（σ）＊，∀u∈E（σ）＊，有映射：E（σ）＊→P。由于C是二元双偶极值码，由文献［3］知，η（F（σ））是一个［8，4］二元双偶码，［8，4］二元自对偶码在等价情况下只有和A8两种，的生成矩阵为：

A8的生成矩阵为：

由于二元双偶极值码的码字重量都为4的倍数，显然η（F（σ））等价于A8。

引理2［13］两个有相同自同构σ的双偶极值码C和C′是等价的充分必要条件是C可经过下列变换得到C′：

（1）7个8循环；

（2）在E1（σ）＊的列中，用α的幂取代原来的值；

（3）在（E1（σ）＊）中，用xt取代x，1≤t≤6。

3.1 K＝2的情形

根据引理2，在等价情况下，K＝2时，E1（σ）＊的生成矩阵为：

此时，E2（σ）＊的生成矩阵为：

把A8生成矩阵中的粗体的1和0分别用7个1和7个0代替［14］，E1（σ）＊、E2（σ）＊、生成矩阵中的每个元素对应一个3×7的循环矩阵，且这个矩阵的第一行对应于生成矩阵中的元素在表1的一个7维数组。这样我们得到了二元双偶极值码在K＝2 的生成矩阵。经过运用Matlab程序，不论i、j、k、l取什么值，该生成矩阵生成的编码最小距离均为8，故得到：

定理1 当E1（σ）＊的维数为2时，不存在有7阶自同构的二元双偶极值码［56，28，12］。

3.2 K＝4的情形

当E1（σ）＊的维数K＝4时，E1（σ）＊的生成矩阵为：

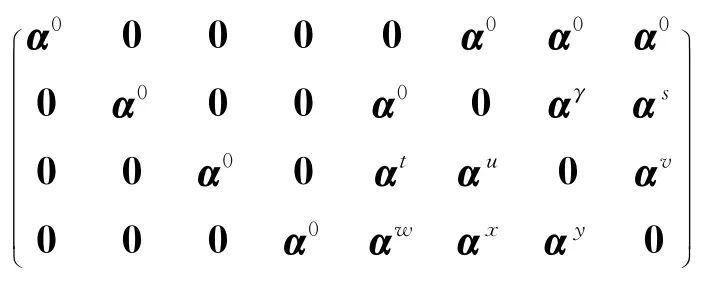
对应E2（σ）＊的生成矩阵为：

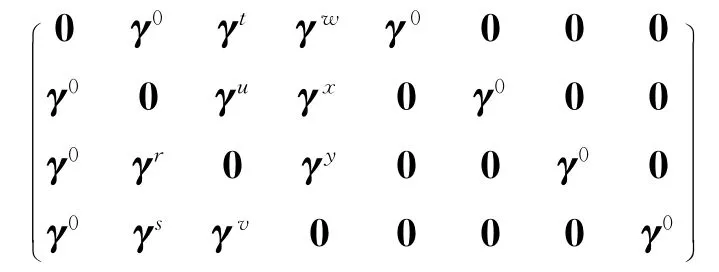
则码长为56 的二元双偶极值码的生成矩阵为：

前4行粗体的1和0都表示元素全为1和0的1×7的行向量，后8行的每一个元素都代表一个3×7的循环矩阵，且循环矩阵αi，γj（i，j＝0，r，s，t，u，v，w，x，y｜r，s，t，u，v，w，x，y∈｛0，1，…，6｝）的第一行对应表1中的元素。粗体0表示3×7的零矩阵，运行Matlab程序，得到当r、s、t、u、v、w、x、y取表2中的值时，二元双偶极值码的最小距离确为12。

Table 2 Values of r，s，t，u，v，w，x，y表2 r，s，t，u，v，w，x，y的取值

表2中＃代表7个0，例如当r、s、t、u、v、w、x、y取值为01＃000＃2时，E1（σ）＊所对应的生成矩阵为：

E2（σ）＊的生成矩阵为：

长度为56的二元双偶极值码的生成矩阵如图1所示。

Figure 1 Generator matrix of the extremal self－dual doubly－even binary codes with length of 56图1 长度为56的二元双偶极值码的生成矩阵

因此，得到如下定理：

定理2 当E1（σ）＊的维数K＝4 时，长度为56的有7－（8，0）型自同构的二元双偶极值码共有75种。

4 有相似型的双偶极值码

由引理2知，对长度为60 的有7－（8，4）型的双偶极值码，η（Fσ（C））是一个［12，6］码，根据文献［3］，［12，6］二元自对偶码在等价情况下只有三种和B12。的生成矩阵为：

在该生成矩阵中，粗体的0代表1×7的零向量，黑体的1代表1×7的行向量，且所有元素全为1，其余的1和0仅表示自身。

因为有7－（8，4）型自同构的长度为60的双偶极值码最小距离为12。显然η（Fσ（C））不等价于同样的讨论可得η（Fσ（C））不等价因此，η（Fσ（C））一定等价于B12。E1（σ）＊、E2（σ）＊的生成矩阵同上。有7－（8，4）型自同构的长度为60的双偶极值码的生成矩阵如下：

注：该生成矩阵后8 行中黑体元素与码长为56的二元双偶极值码生成矩阵中后8行的元素一致。

长度为60的双偶极值码的最小距离为12，对生成矩阵运行Matlab程序，得到与长度为56的双偶极值码相类似结论：

定理3 当E1（σ）＊的维数为2时，不存在有7阶自同构的二元双偶极值码［60，30，12］。

定理4 当E1（σ）＊的维数K＝4 时，长度为60的有7－（8，4）型自同构的二元双偶极值码共有3种（r、s、t、u、v、w、x、y取值为最后三个值时）。

由引理1知，长度为66、68、70的码，都不存在有7－（8，m）（m＝10，12，14）型的自同构。对长度为62和64的双偶极值码进行相似讨论，得：

定理5 当E1（σ）＊的维数为2时，不存在有7阶自同构的二元双偶极值码［62，31，12］和［64，32，12］。

定理6 当E1（σ）＊的维数K＝4 时，长度为62的有7－（8，6）型自同构的二元双偶极值码共有2 308种。

定理7 当E1（σ）＊的维数K＝4 时，长度为64的有7－（8，8）型自同构的二元双偶极值码共有2 976种。

5 结束语

本文针对线性码中长度为50到60之间的双偶极值码进行讨论，试图找出其生成矩阵和分类情况，但对长度较长的线性码，要找到这样的线性码非常困难。长度越长，码字的复杂程度越高，因此总是限定其有一个特殊的自同构来进行讨论。根据特殊自同构将它分成几个长度较短的线性码的直和，来得到其生成矩阵和分类情况。长度为52的线性码最小距离为10，它不存在双偶极值码，长度为56、60、62和64的双偶极值码分别有7－（8，0）型、7－（8，4）型、7－（8，6）型和7－（8，8）型的自同构。本文得到了这些情形下的生成矩阵及分类情况，这些对解码工作的发展有着积极意义。对长度更长的双偶极值码和这些码的应用是本文作者研究的下一个目标。

［1］ Ning Ping.Exploration for parallel computing of CRC16checksum on FPGA［J］.Computer Engineering ＆Science，2014，36（6）：1023－1027.（in Chinese）

［2］ Huffman W C.On the classification and enumeration of selfdual codes［J］.Finite Fields and Their Appplications，2005，11（3）：451－490.

［3］ Pless V.A classification of self－orthogonal codes overGF（2）［J］.Discrete Math，1972，3：209－246.

［4］ Bouyuklieva S，Yankov N，Kim J.Classification of binary selfdual［48，24，10］codes with an automorphism of odd prime order［J］.Finite Fields and Their Applications，2012，18（6）：1104－1113.

［5］ Aguilar－Melchor C，Gborita P，Kim J－L，et al.Classification of extremal and s－extremal binary self－dual codes of length 38［J］.IEEE Transactions on Information Theory，2012，58（4）：2253－2262.

［6］ Yorgov V.The extremal codes of length 42 with automorphism of order 7［J］.Discrete Mathematics，1998，190：201－213.

［7］ Yorgov V.Erratum to“The extremal codes of length 42 with automorphism of order 7”［J］.Discrete Mathematics，2011，311：1860－1861.

［8］ Bouyuklieva S，Yankov N，Russeva R.Classification of the binary self－dual［42，21，8］codes having an automorphism of order 3［J］.Finite Fields and Their Applications，2007，13（3）：605－615.

［9］ Goodwin V，Yorgov V.New extremal self－dual doubly－even binary codes of length 88［J］.Finite Fields and Their Applications，2005，11（1）：1－5.

［10］ Conway J H，Sloane N J A.A new upper bound on the minimal distance of self－dual codes［J］.IEEE Transactions on Information Theory，1990，36（6）：1319－1333.

［11］ Yorgov V Y.Binary self－dual codes with automorphism of odd order［J］.Problems of Inform Transmission，1983，19：11－24.

［12］ Han S，Kim J－L，Lee H，et al.Construction of quasi－cyclic self－dual codes［J］.Finite Fields and Their Applications，2012，18（3）：613－633.

［13］ Bouyuklieva S，Bouyukliev I.An algorithm for classification of binary self－dual codes［J］.IEEE Transactions on Information Theory，2012，58（6）：3933－3940.

［14］ Wang Rong，Wang Jun－xin.［52，26，10］binary self－dual codes with type of（17，3，1）［J］.Computer Engineering and Applications，2012，48（19）：46－48.（in Chinese）

附中文参考文献：

［1］ 宁平.FPGA 上实现CRC16纠错编码并行计算的探讨［J］.计算机工程与科学，2014，36（6）：1023－1027.

［14］ 王荣，王俊新.有（17，3，1）型的二元自对偶编码［52，26，10］［J］.计算机工程与应用，2012，48（19）：46－48.