云环境下基于Bayesian主观信任模型的动态级调度算法*
齐 平,王福成,朱桂宏
(铜陵学院数学与计算机学院,安徽 铜陵244000)
1 引言
云计算(Cloud Computing)是继并行计算、分布式计算、网格计算后的新型计算模式[1]。云计算平台利用虚拟化技术将多种计算资源(包括网络、服务器、存储、应用和服务等)在云端进行整合,对资源进行统一管理和调度,使得这些资源可以根据负载的变化动态配置,以达到最优化的资源利用率。因此,采用何种资源提供策略对这些大规模资源进行组织和管理,实现资源提供的高效灵活和按需分配,对云计算具有重要意义。
近些年在云计算资源管理方面已有了较多的研究,针对不同的计算任务和优化目标,云资源调度算法可以分为以下几类:(1)以提高资源利用率和降低任务完成时间为目标[2,3];(2)以降低 云计算中心能耗为目标[4~6];(3)以提 高 用户QoS(Quality of Service)为目标[7,8];(4)基于经济学的云资源管理模型研究[9,10];(5)多目标优化的混合算法[11,12]。
然而,由于云环境中包含着大量分散、异构资源,这些资源不仅地理位置分布广泛,甚至属于不同的自治系统,因而这些资源节点往往具有动态性、异构性、开放性、自愿性、不确定性、欺骗性等特征。云服务的可靠性是指用户提交的服务被成功完成的概率,是从用户的角度反映云完成用户提交服务的执行能力。在拥有无数资源节点的云环境中,节点的不可靠不可避免,因此如何获取可信的云资源,并将应用任务分配到值得信任的资源节点上执行成为云资源调度算法研究中急需解决的关键问题之一。
目前,在国内外分布式系统资源管理的相关研究中,有关如何获取可信资源的研究已经取得了不少成果。Dogan A 等人首先提出了RDLS(Reliable Dynamic Level Scheduling)算法,研究如何在异构分布式系统中获取可信资源[13,14]。在此基础上,随后的研究包括:Dai Yuan-sun等人[15]提出了网格服务可靠性概念,采用最小档案扩展树对网格服务可靠性进行了求解;Levitin G[16]针对星型网格,提出了考虑服务可靠性和服务性能的信任评估算法;Foster I等人[17]将云服务和网格服务进行比较,给出了云服务可靠性的评估方法。上述文献采用不同的信任模型,从不同角度研究网格服务、云服务的可靠性,并给出了相应的调度算法,有效地提高了任务执行的成功率。
然而,自从Blaze M[18]首先提出了信任管理概念后,Josang A 等人[19,20]引入证据空间(Evidence Space)的概念,以描述二项事件后验概率的Beta分布函数为基础,将信任分为直接信任和推荐信任,根据节点间交互的肯定经验和否定经验计算出实体能够完成任务的概率,并以此概率作为实体信任度的度量。基于证据的信任模型都是通过量化实体行为和计算实体信任度来评估实体间的相互信任关系。而在上述研究中,建立的信任评估模型并未考虑资源节点本身的行为特性。文献[21,22]在此基础上,综合考虑时间、权重等相关因素,利用Bayesian方法构造了一个基于节点行为的可信度评估模型,并将其引入网格服务、云服务的可靠性研究中,分别提出了Trust-DLS和Cloud-DLS 算法。
在文献[21,22]所提出的算法中,通常假设资源分配具有公平性,即在有限的资源条件下,节点之间不会因为争夺资源而相互影响,造成损害,任意两对节点之间的交互都是独立的,交互信息都是真实可靠的。然而,在真实的云环境中,为得到更多的资源,节点可能会通过需求欺骗、长期占用等手段非法使用资源,成为自私节点而对资源分配的公平性造成破坏;此外,在非可信网络环境中,节点也有可能被攻击而成为恶意节点,提供虚假的交互信息。这些自私节点和恶意节点蚕食系统资源,在破坏资源分配公平性的同时,使得云平台内正常节点因资源需求无法满足而不能正常作业,从而降低系统的可靠性。节点间交互过程中可能出现的这些威胁,都会导致作为信任值评估证据的样本空间不一定完整和可靠,因而现有的信任评估模型不太适用。
Bayesian方法是建立在主观概率的基础上,通过对历史经验、各方面信息等客观情况的了解,再进行分析推理后得到的对特定事件发生可能性大小的度量,本文借鉴社会学中人际关系信任模型,旨在构造一种云环境下基于Bayesian方法的主观信任管理模型。本文提出的Bayesian主观信任模型是在文献[21,22]基础上,并对其进行了较大的扩充,主要体现在以下几点:(1)研究了信任的定义、描述、评估方法和合成、传递、推导机制;(2)针对原有信任模型对推荐信任关系的评估较为简单的问题,细化了推荐信任关系及相应的评估方法;(3)考虑网络中节点的不确定性、欺骗性等问题,研究风险因素,引入了惩罚机制和分级剪枝过滤机制。最后将该模型引入传统的DLS算法中,提出了基于Bayesian主观信任管理模型的动态级调度算法,仿真实验结果表明,提出的BST-DLS 算法能够以较小的调度长度为代价,有效地提高云环境下任务执行的成功率。
2 Bayesian主观信任模型
人们在生活中进行各种各样的交易、交互和通信都是基于一个基础理念——信任。信任本质上是一个社会心理关系,在人际关系网络中,信任是对他人可信行为的评价,而个体的可信与否往往取决于其他个体的推荐。云计算平台下的资源节点与人际关系网络中的个体具有很大的相似性,这表现在以下几点:(1)节点在和其他资源节点交互时,会留下反映其行为特征的交互信息;(2)不同的节点可以通过其不同的主观判断标准选择交互节点,节点具备信任的主观性;(3)节点之间的交互关系可以是一对一、一对多,也有可能是多对多或者多对一;(4)和信任关系类似,节点间的交互具有一定的传递性。因此,云环境下的资源节点可以根据其历史交互经验进行信任评估。
在信任评估模型中,节点间信任关系分为两类:一类为直接信任关系,如图1a所示,当节点i和节点j之间存在可作为可信度评估依据的直接交互,即可以设法估算出直接交互成功的概率,称为直接信任度评估,用Tdt表示直接信任度;另一类为推荐信任关系,如图1b所示,当节点i和节点j之间不存在可作为可信度评估的直接交互,而节点i可以获取其他节点(例如节点k)关于节点j的可作为可信度评估依据的交互,这种需要通过第三方来建立的信任关系,称为推荐信任度评估,用Trt表示推荐信任度。
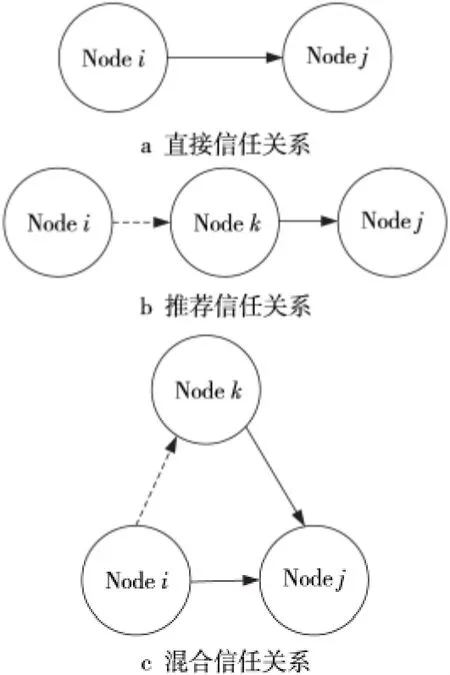
Figure 1 Trust relationship among nodes图1 节点间信任关系
当同时存在直接信任关系和推荐信任关系时,如图1c所示,为混合信任关系,需要将上述两种信任关系进行合并,得到总体的信任评估。如同在人际关系网络中,当个体之间进行信任评估时,往往既存在直接信任关系也存在推荐信任关系,不同的个体由于其个性、情绪等主观因素不同,具有不同的量化判断标准。本文选择线性函数作为两种信任关系的合并函数,如式(1)所示:

其中,λ表示个体对两种信任关系的调节因子,当0<λ<0.5时,表示个体更信任推荐信任关系,而当λ>0.5时,表示个体相信直接交互经验超过其他个体的推荐经验。
2.1 直接信任关系
直接信任是节点根据历史交互经验,对目标节点未来行为的主观期望,在这里借鉴文献[23]提出的模型,根据二项事件后验概率分布服从Beta分布来求解信任值。设两个云资源节点i和j,使用二项事件(交互成功/交互失败)描述它们之间的交互结果;当节点i和j之间发生n次交互后,其中成功交互的次数为α,失败交互的次数为β;同时假设随机变量x为一次交互过程中获得成功的概率,且x服从(0,1)的均匀分布U(0,1)。定义i对j的直接信任度Tdt为:
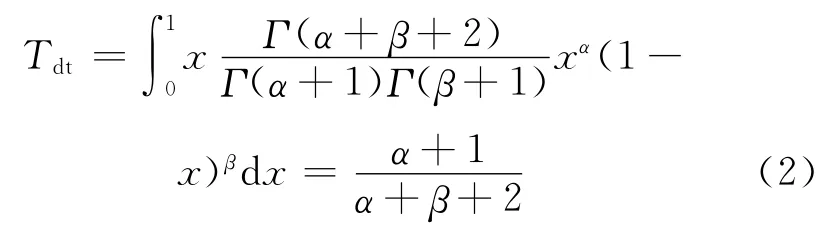
由式(2)可以看出,直接信任关系的评估与节点间成功交互次数以及总交互次数有关。虽然通过式(2)可以得到节点间的直接信任度,然而当节点间没有交互或者交互较少时,较少的样本数将不足以评估节点间直接信任关系。
针对该问题,本文使用区间估计理论[24]对信任度的置信水平进行度量,设(Tdt-δ,Tdt+δ)为直接信任度Tdt的置信度为γ的置信区间,δ为可接受误差,则Tdt的置信度γ计算公式如下:

由于区间估计的置信度与精度相互制约,因此先选定置信度阈值为γ0,然后通过增加总的交互次数n提高精度,直到达到可接受水平,即γ≥γ0时,可以根据这时的直接交互信息进行信任度计算。此时的样本容量n0、可接受误差δ和置信度阈值γ0之间的关系由式(4)给出:

通过上述分析可知,根据节点间直接交互样本的置信度值,可以将直接信任关系评估作如下设定:(1)当节点间不存在直接交互,或交互样本置信度值γ<γ0时,设定节点间的直接信任度Tdt=1/2;(2)当交互样本置信度值γ≥γ0时,节点间的直接信任度Tdt按照式(2)计算。
2.2 推荐信任关系
推荐信任关系由两类或多类直接交互关系形成,由于推荐信任关系涉及多方实体的交互关系,因而较难评估,这表现在:(1)根据推荐节点之间的相互关系,可以把推荐信任关系进一步分为单径信任推荐关系和多径信任推荐关系;(2)由于恶意节点和自私节点的存在,在推荐信任关系中,并不能保证所有的推荐者都是可信的,也不能确定所有可信的推荐者所推荐的信息都是准确的。
因此,针对推荐信任关系的上述特点,借鉴人类接受推荐信息的心理过程,本文利用Bayesian方法模拟人类判断推荐信息的认知模型,建立抵御恶意节点推荐的机制,使得信任模型更加合理。
2.2.1 单径推荐信任关系
如图2所示为单径推荐信任关系模型,在单径推荐信任关系传递过程中,推荐信任的传递由节点间的信任关系和该信任关系的可靠程度(即信任强度)构成。
定义1 信任强度是指在推荐信任传递的过程中,节点间信任关系的可靠程度;它刻画了主体节点对中间推荐节点和目标节点之间信任关系的相信程度。信任强度用S表示,且满足0≤S≤1。
定义2 推荐信任关系由中间推荐节点对目标节点的信任关系和该信任关系的可靠程度组成,可以表示为推荐信任向量(T,S)。
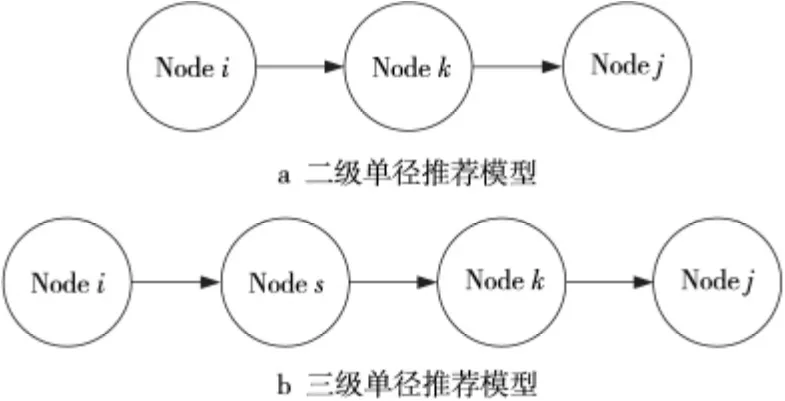
Figure 2 Recommendation trust relationship(single path)图2 单径推荐信任关系
图2a为含有三个节点的二级单径推荐关系,设节点i对中间推荐节点k的直接信任度为节点k对目标节点j的直接信任度为则节点j向节点i传递的推荐信任向量为(Tkj,Skj)。其中Skj定义为主体节点i对节点k传递信任信息的相信程度,因此满足式(5):

图2b为含有四个节点的三级单径推荐关系,设节点i、s、k、j之间的直接信任度分别为和则节点j向节点s和节点i传递的推荐信任向量为(Tkj,Skj)和(Tsj,Ssj),满足式(6):

同理可以得到多级单径推荐关系的评估方法,当存在n个节点(1,2…,n)的n-1级单径推荐关系时,节点n对节点1 的推荐信任向量为(T2n,S2n),其中
通过上述公式可以发现,推荐信任在传递的过程中经过了若干中间推荐节点,推荐信任值发生了衰减。而这正符合人类判断推荐信息的认知模型,即经过多人传递的推荐信息,其可信度逐渐降低。
2.2.2 多径推荐信任关系
在云平台中,资源节点之间常常有多条路径,图3所示为两条路径的推荐信任关系模型:包含路径{i,k,s,j}和路径{i,d,f,j}。设节点j通过两条路径向i传递的推荐信任向量分别为(Tkj,Skj)和(Tdj,Sdj),那么节点i可以根据式(7)得到节点j的多径推荐信任。

其中,ω1和ω2为两条路径推荐信任的权重,有ω1=Skj/(Skj+Sdj),ω2=Sdj/(Skj+Sdj)。同理可以得到多级(n级)多径推荐信任关系模型。设多条路径推荐信任向量分别为{(T1,S1),(T2,S2),…,(Tn,Sn)},那么节点i可以根据式(8)得到节点j的多径推荐信任。

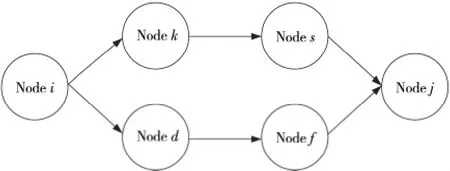
Figure 3 Recommendation trust relationship(multipath)图3 多径推荐信任关系
2.2.3 推荐信任关系的进一步讨论
在实际的云计算平台中,云资源节点除正常节点外,通常同时还存在自私节点和恶意节点,因此并不能保证所有推荐节点传递的推荐信息都是非恶意的。同时,当推荐路径中存在恶意节点时,该推荐路径传递的推荐信息也是不合理的。恶意节点和恶意推荐往往会提供虚假的交互信息或篡改历史交互结果,导致作为信任值评估证据的样本空间不一定完整和可靠。
针对上述问题,本文在评估推荐信任关系之前,首先建立分级剪枝过滤机制,过滤偏离直接信任度过大的推荐和可信度较低的推荐;再通过惩罚机制对多径推荐信任的终点是同一推荐节点这一易出现恶意推荐的情况进行讨论。
(1)分级剪枝过滤机制。
如前文所述,节点可以通过搜索网络中的其他节点和目标节点的历史交互信息获取推荐信任关系。在多径推荐信任关系模型中,主体节点和目标节点之间往往会存在多条推荐路径(推荐路径可以为一个推荐节点,也可以由多个推荐节点组成的多级推荐关系)。然而,由于恶意节点的存在,并不是所有的推荐信息都是可靠的,因此需要过滤掉恶意和无用的推荐信息。参照人类接受推荐的认知过程可知:①可信度较低的推荐者的推荐信息参考价值较低;②偏离直接交互经验或心理预期较大的推荐难以接受。因此,本文使用分级剪枝过滤机制在可选推荐路径中筛选有用的推荐信息,对推荐信任度较低或推荐偏差较大的推荐进行剪枝过滤。
定义3(推荐偏差) 设节点i和节点j的直接信任度为推荐路径Pk的推荐信任度为则推荐偏差dk为:

其中,推荐路径Pk推荐信任度的偏差dk越大,被接受的可能性越小,当节点i和节点j不存在直接交互时,设定直接信任度的值为1/2。
对于信任度较高的推荐,如果其推荐偏差较大,在一定的偏差范围内可以接受该推荐,而对于信任度较低的推荐,可接受的偏差范围则较小。本文使用文献[25]提出的信任等级划分方法,对推荐路径按照其信任度的不同划分其等级,并提供不同的可接受范围。信任等级划分方法如式(10)所示:

其中,x表示信任度,l(x)表示其信任等级。
按照信任度划分为不同信任等级后,其分级剪枝过滤过程如下:
①对于推荐路径{P1,P2,…,Pn},根据路径推荐信任度将其划分为l+1个等级,按照不同的等级包含在不同的推荐路径集合{Pk}l中,对每一信任等级l,其可接受推荐偏差为εl。
②设0<m<l,对于信任等级低于m的较低信任度的推荐路径集合进行剪枝,排除低信任度的推荐路径。
③对于剩余推荐路径集合{Pk}(l|l>m),推荐路径Pk的可接受范围由其推荐偏差决定,如式(11)所示:

(2)惩罚机制。
在多径推荐信任关系模型中,当多条推荐路径的终点为同一推荐节点时,如果该节点恰好为恶意节点进行恶意的信任推荐,那么最终得到的评估结果一定是不合理的。如图4所示,当推荐路径{i,k,s}和{i,d,f}的终点为节点m时,节点m的信任传递对节点i和节点j之间的推荐信任评估有着重要意义。针对该问题,本文引入惩罚机制[26]并加以讨论。

Figure 4 Punishment mechanism in recommendation trust relationship(multipath)图4 多径信任推荐关系中的惩罚机制
设多径推荐信任关系模型中包含n个节点,其中含有c个自私节点和z个恶意节点,定义I为推荐路径上第1个推荐节点是恶意节点的事件,Hk表示推荐路径上第一个恶意节点占据第k个位置的事件,则从第k个位置开始推荐路径上存在恶意节点的事件可以用Hk+=Hk∨Hk+1∨Hk+2∨…表示。因此,当推荐路径上存在恶意节点的情况下,设恶意节点冒名正常节点的概率为P(I|H1+),满足式(12):

针对上述问题,引入惩罚因子ps,用于调整多径信任推荐中一些推荐路径的终点可能是同一个推荐节点时,该节点为恶意节点对推荐信任评估带来的影响。如图4所示,当两条推荐路径的推荐信任向量分别为(Tkj,Skj)和(Tdj,Sdj),且两条推荐路径中含有相同的节点m时,节点i可以根据式(13)得到节点j的新的多径推荐信任:

其中,ω1和ω2为两条路径推荐信任的权重。
在引入惩罚因子后,恶意节点冒名正常节点的概率P′(I|H1+)为:

由式(12)和式(14)可以看出,引入惩罚因子ps后,恶意节点冒名正常节点的概率减少,能够在一定程度上提高系统的可靠性。
2.3 时间因素
为体现信任评估的动态性,本文考虑时间因素对信任评估的影响。借鉴人类对历史信息的认知方法可知,不同时期的历史交互信息对信任评估过程产生的影响是不同的,越接近的历史交互信息影响越大,而时间跨度越长的历史交互信息影响越小直至对评估失去意义而不对其进行考虑。
类似文献[27],在这里采用时间分段的概念,将时间段设置为一天,并引入时间影响力衰减因子η刻画不同时期历史交互信息的重要程度。因此,对于n个时间段,设时间段i的成功交互和失败交互次数分别为αi和βi,则第n个时间段后总的交互成功次数和失败次数α(n)和β(n)如式(15)所示:

其中,0≤η≤1,η=0表示只考虑最近一次的历史交互影响,而η=1表示不考虑时间影响力衰减因子。
3 基于Bayesian主观信任模型的动态级调度算法
根据上一节讨论的Bayesian主观信任模型,本文充分考虑云资源节点的可信度,针对节点中存在恶意推荐问题,扩展了传统的DLS 算法[28],使得基于有向无环图(DAG)的云资源调度算法更加全面合理。
DLS算法是一种静态启发式的表调度算法,主要用于将基于DAG 的应用分配到一个异构的资源节点集合上。在调度的每一步,DLS 算法通过寻找具有最高“动态级”的任务vi-资源mj对,从而将任务vi调度到资源mj上执行,完成任务分配。任务-资源(vi-mj)对的动态级DL(vi,mj)定义如式(16)所示:

其中,SL(vi)为任务静态级,在一个调度期间内为常数,指DAG 中从任务vi到终止节点的最大执行时间;表示任务vi在资源mj上执行的时间,表示任务vi调度到资源mj上所需输入数据可获得的时间,表示资源mj空闲时可以用于执行任务vi的时间;Δ(vi,mj)表示资源mj的相对计算性能,为任务vi在所有资源上的平均执行时间与其在资源mj上的执行时间之差。
当任务调度到目标节点上执行时,可信度反映目标节点提供服务的可靠程度,DLS算法考虑资源的异构性,能够适应资源异构性的特征,但没有考虑到云资源的可信度对任务调度效果的影响。为解决该问题,文献[22,23]考虑节点间行为特性和历史交互信息,提出了可信动态级调度算法,并应用到网格服务和云服务中。然而,该算法假设资源分配具有公平性,认为各节点给出的历史交互信息都是真实可靠的,并未考虑自私节点和恶意节点对交互信息和推荐信任评估结果的影响。因此,本文引入分级剪枝过滤机制和惩罚机制,提出云环境下基于Bayesian主观信任模型的动态级调度算法(BST-DLS),对于任务vi和云资源节点nj,其可信动态级BST-DL(vi,mj)定义如式(17)所示:

其中,TS(vi,nj)表示云资源节点ns调度任务vi到云资源节点nj上时对nj可信度的评估,即第2节中讨论的合并信任度T。
4 仿真实验及结果分析
为验证提出的信任评估模型和动态级调度算法,本文在PlanetLab 环境[29]中设计了基于云仿真软件CloudSim[30]的实验平台。分布于全球的计算机群项目PlanetLab始于2003年,由普林斯顿大学、华盛顿大学、加州大学和Intel研究人员共同开发,其目标是提供一个用于开发下一代互联网技术的开放式全球性测试实验平台。在Planet-Lab的网络模拟实验环境中,设定节点数和节点之间的链路数预先给定,链路间的数据传输速度介于[1,10]Mbit/s。
云仿真软件CloudSim 是一个通用、可扩展的新型仿真框架,它通过在离散事件模拟包SimJava上开发的函数库支持基于数据中心的虚拟化建模、仿真功能和云资源管理、云资源调度的模拟。同时,CloudSim 为用户提供了一系列可扩展的实体和方法,用户根据自身的要求调用适当的API实现自定义的调度算法。本文所有的仿真实验中,每组实验分为10次,最终结果采用平均值。相关实验参数设置如下:根据文献[22,23]讨论,信任关系调节因子λ和时间影响衰减因子η均设置为0.8;式(3)和式(4)中δ和γ0的取值分别为0.1 和0.95;同时按照式(18)将信任等级划分如下:
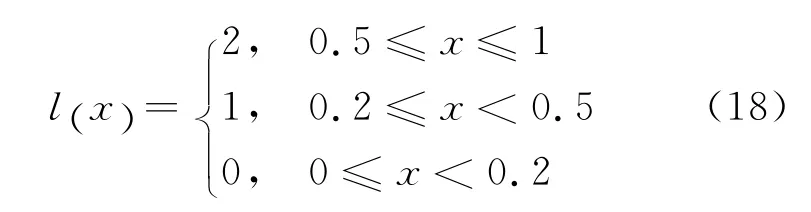
其中,对于信任等级l(x)=0 的推荐路径进行剪枝,对于信任等级l(x)=1 和l(x)=2 的推荐路径,其可接受偏差范围εl分别设为ε1和ε2。
在实际的云计算平台中,由于不同类型的恶意节点通过组合都可以产生一类新的恶意节点,因此对恶意节点的刻画较为困难。为简化实验,本文仅对以下几类节点进行测试:(1)简单恶意节点,这类节点提供的服务是不真实的;(2)诋毁恶意节点,这类节点诋毁与其交互过的正常节点,其目的是借此降低其信誉度;(3)合谋恶意节点,这类节点通过修改交易信息,夸大同伙节点的可信度,同时诋毁正常节点。此外,设置两类自私节点,分别占节点总数的10%,它们在分配到任务时,以80%和50%的概率执行任务失败。
本文首先对提出的惩罚机制和分级剪枝过滤机制进行讨论,主要讨论惩罚因子ps以及分级剪枝过滤机制中的参数对信任度评估的影响。
4.1 信任模型的有效性
(1)惩罚机制ps。
为考察多径推荐信任关系中引入惩罚机制的有效性,当惩罚因子ps的取值分别为0.3、0.7、1时,对任务执行成功率进行比较。
实验中相关参数设置如下:云资源节点数为200,链路数为200,任务数为100,设定网络中存在的恶意节点为提供不真实服务的简单恶意节点。
由式(13)可知,惩罚因子ps可以调节惩罚机制的影响力,当ps=1 时,未使用惩罚机制,而当ps的值越小则惩罚机制的影响力越强。如图5所示,当网络中的恶意节点不超过20%时,ps=1和ps=0.3、ps=0.7的任务执行成功率相似;随着网络中的恶意节点比例增加,任务执行成功率均有不同程度的降低,而当恶意节点比例超过35%时,未考虑惩罚机制时的任务执行成功率下降速度较快,且数值明显低于其他两类,这充分体现了本文提出的惩罚机制的有效性。

Figure 5 Impact of penalty factor ps on average ratio of successful execution图5 惩罚因子ps 对平均执行成功率的影响
值得一提的是,当网络中恶意节点所占比例小于10%时,未使用惩罚机制的任务执行成功率略高于使用惩罚机制的任务执行成功率。这是由于在多径推荐信任关系模型中,惩罚机制是针对多条推荐路径的终点为同一推荐节点,且该节点恰好为恶意节点的情况。因此,如果网络中存在较少的恶意节点或不存在恶意节点,则该惩罚机制会在一定程度上降低算法选择最可靠路径的可能性,从而使得任务执行成功率有一定程度的降低。
(2)分级剪枝过滤机制。
为考察本文提出分级剪枝过滤机制的有效性,对于信任等级l(x)=1和l(x)=2的推荐路径,对其可接受偏差(ε1,ε2)分别取(0.1,0,2)、(0.2,0,4)和不考虑该机制时的任务执行成功率进行比较。为表达清楚,用Ε1、Ε2和Ε3分别表示可接受偏差(ε1,ε2)的取值为(0.1,0,2)、(0.2,0,4)和未使用分级剪枝过滤机制的情况。
其他实验环境设置如下:云资源节点数为200,链路数为200,任务数为100,惩罚因子ps=0.7,设定网络中存在的恶意节点为提供不真实服务的简单恶意节点。
实验结果如图6所示,随着网络中恶意节点的比例的增加,Ε1、Ε2和Ε3的任务执行成功率均有不同程度的降低,其中未考虑分级剪枝过滤机制的Ε3成功率降低较快,而Ε1和Ε2在恶意节点比例超过30%时仍然具有相对较高的任务执行成功率,说明了本文提出分级剪枝过滤机制的有效性。
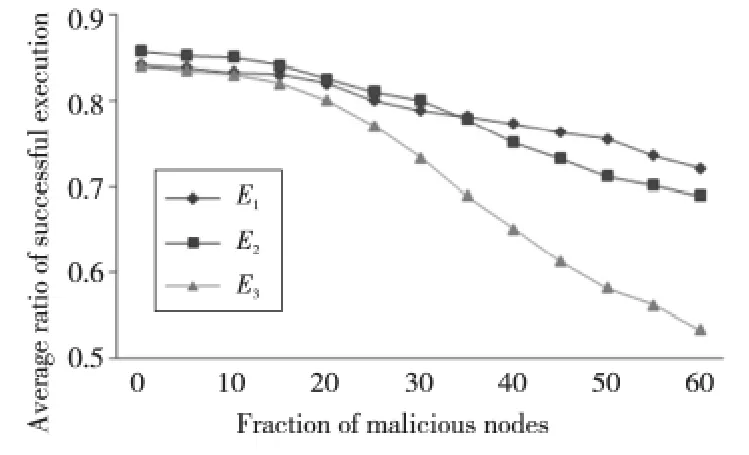
Figure 6 Impact of hierarchical pruning mechanism on average ratio of successful execution图6 分级剪枝过滤机制对平均执行成功率的影响
当恶意节点比例超过40%时,可以看出E1的执行成功率略高于E2,说明在恶意节点比例较大的网络环境中,适合采用更小的可接受范围以保证任务执行的可靠性。
4.2 各类恶意节点情况下的比较
该仿真实验针对网络中存在三类典型的恶意节点,即简单恶意节点、诋毁恶意节点和合谋恶意节点,比较本文提出的BST-DLS算法、Cloud-DLS算法和传统的DLS算法在不同类型恶意节点情况下的性能。实验相关参数设置如下:云资源节点数为200,链路数为200,任务数为100,设置惩罚因子ps为0.7,可接受偏差(ε1,ε2)取(0.1,0,2)。
(1)简单恶意节点。图7为恶意节点为简单恶意节点情况下,BST-DLS算法、Cloud-DLS算法和传统的DLS算法的任务执行成功率。从图7可以看出,当增加恶意节点所占比例时,三种算法的任务执行成功率都呈下降趋势。BST-DLS算法与Cloud-DLS算法、DLS算法相比下降速度最慢,当恶意节点比例达到40%时,Cloud-DLS 算法和DLS算法任务执行成功率分别只有50.9%和18.9%,而BST-DLS算法能够有效地抵御恶意节点,任务执行成功率为77.4%,说明BST-DLS 算法能够有效抑制简单恶意节点的攻击。

Figure 7 Average execution success ratio(simple malicious nodes)图7 简单恶意节点情况下的平均执行成功率
(2)诋毁恶意节点。图8为恶意节点为诋毁恶意节点情况下,BST-DLS算法、Cloud-DLS算法和传统的DLS算法的任务执行成功率。诋毁恶意节点通过提供不真实服务诋毁与其交易过的可信节点,通过图8可以看出,虽然当增加恶意节点比例时,三种算法的任务执行成功率都呈下降趋势,但是在有40%为诋毁恶意节点的情况下,BST-DLS算法仍然具有75.7%的任务执行成功率,明显高于其他两种算法,较为有效地抑制了诋毁恶意节点的影响。
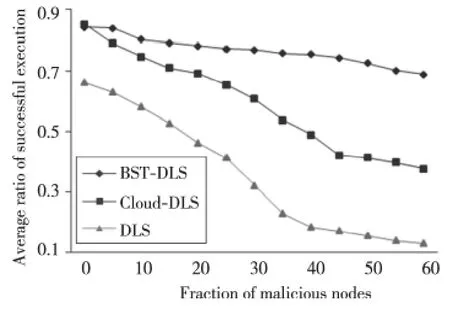
Figure 8 Average execution success ratio(denigration malicious nodes)图8 诋毁恶意节点情况下的平均执行成功率
(3)合谋恶意节点。图9为恶意节点为合谋恶意节点情况下,BST-DLS算法、Cloud-DLS算法和传统的DLS算法的任务执行成功率。合谋恶意节点通过提供不真实服务信息夸大同伙节点可信度的同时,也会诋毁与其交易过的可信节点,试图降低可信节点的信任度。由图9可见,当增加合谋恶意节点的比例时,三种算法的任务执行成功率同样都呈下降趋势,在有40%为合谋恶意节点的情况下,BST-DLS 算 法 具 有72.9%的 任 务 执 行 成 功率,明 显 高 于Cloud-DLS 算 法 和DLS 算 法 的47.1%和19.6%。

Figure 9 Average execution success ratio(collusion malicious nodes)图9 合谋恶意节点情况下的平均执行成功率
由上述实验结果可以看出,本文提出的BSTDLS算法在网络中存在三类典型的恶意节点的情况下,通过分级剪枝过滤机制和惩罚机制可以有效地抑制恶意节点,保证任务执行的可靠性。而Cloud-DLS算法和DLS算法由于并未对恶意节点作任何处理,因此当恶意节点比例增加时,恶意节点很容易获得较高的可信度。同时,在网络中存在诋毁恶意节点和合谋恶意节点的情况下,往往可信节点的信任度还会由于恶意节点的诋毁反而变得较低。恶意节点由此得到大量的交互,并使得这些交互失败而导致系统可靠性降低。
4.3 不同节点数情况下的比较
该仿真实验在网络中具有不同节点数的情况下,比较本文提出的BST-DLS 算法、Cloud-DLS算法和DLS算法在任务执行成功率和调度长度方面的性能。实验相关参数设置如下:设定实验中随机产生100~1 000个云资源节点,任务数为100,链路数为200;设置惩罚因子ps为0.7,可接受偏差(ε1,ε2)取(0.1,0,2),设定网络中存在的恶意节点为提供不真实服务的简单恶意节点,恶意节点占网络中节点的比例为40%。

Figure 10 Average ratio of successful execution of DLS,Cloud-DLS and BST-DLS algorithms with varying numbers of nodes图10 不同节点数下DLS、Cloud-DLS和BST-DLS的平均执行成功率比较
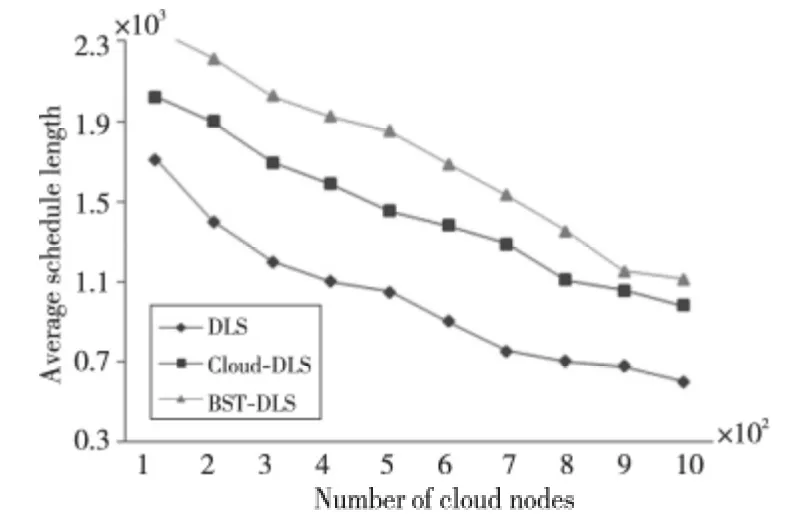
Figure 11 Average schedule length of DLS,Cloud-DLS and BST-DLS algorithms with varying numbers of nodes图11 不同节点数下DLS、Cloud-DLS和BST-DLS的平均调度长度比较
由图10、图11可见,当网络中恶意节点比例为40%时,随着网络中总节点数的增加,三种算法的任务执行成功率均略有提高,而调度长度均有不同程度的减少。图10中,BST-DLS算法的平均任务执行成功率为82.39%,明显高于Cloud-DLS算法的60.89%和DLS算法的23.48%,充分体现了本文提出BST-DLS算法的有效性。图11中本文提出的BST-DLS算法的平均调度长度为1 721.7,高于Cloud-DLS 算 法 的1 447.1 和DLS 算 法 的1 009.6。
综上可知,BST-DLS算法与DLS算法相比平均执行成功率和平均调度长度的增加分别为250.89%和70.53%,与Cloud-DLS算法相比平均执行成功率和平均调度长度的增加分别为35.3%和18.97%。可见,本文提出的BST-DLS 算法虽然能够显著地提高系统的可靠性,但在获得较高的任务执行成功率的同时,也牺牲了一定的调度长度,且该算法在可靠性方面性能的提高远高于所增加的调度长度。
5 结束语
本文深入研究云环境下节点间直接信任及推荐信任的传递与合成问题,针对云环境中存在自私节点和恶意节点的情况,引入惩罚机制和分级剪枝过滤机制,通过对云环境下节点可信度的评估,提出一种云环境下基于Bayesian方法的主观信任模型和相应的可信动态级调度算法。该算法作为一种有效的评价分析和推导工具,能够为云环境中主体节点的信任决策提供有效的支持,使得应用任务在值得信赖的环境下运行。本文的下一步工作将考虑云环境中的相关安全机制与时间花费、价格花费等服务质量因素相结合,满足不同用户的服务质量要求。
[1] Rajkumar B,Shin Y C,Broberg V S,et al.Cloud computing and emerging IT platforms:Vision,hype,and reality for delivering computing as the 5th utility[J].Future Generation Computer Systems,2009,25(6):599-616.
[2] Darbha S,Agrawal D P.Optimal scheduling algorithm for distributed memory machines[J].IEEE Transactions on Parallel and Distributed Systems,2002,9(1):87-95.
[3] Lee Y C,Zomaya A Y.A novel state transition method for metaheuristic-based scheduling in heterogeneous computing systems[J].IEEE Transactions on Parallel and Distributed Systems,2008,19(9):1215-1223.
[4] Zhu D,Mosse D,Melhem R.Power-aware scheduling for and/or graphs in real-time systems[J].IEEE Transactions on Parallel and Distributed Systems,2004,15(9):849-864.
[5] Kim K H,Buyya R,Kim J.Power aware scheduling of bagof-tasks applications with deadline constraints on DVS-enabled clusters[C]∥Proc of the 7th IEEE International Symposium on Cluster Computing and the Grid,2007:541-548.
[6] Bunde D P.Power-aware scheduling for makespan and flow[J].Journal of Scheduling,2009,12(5):489-500.
[7] Li M S,Yang S B,Fu Q F,et al.A grid resource transaction model based on compensation[J].Journal of Software,2006,17(3):472-480.
[8] Xu B M,Zhao C Y,Hua E Z,et al.Job scheduling algorithm based on Berger model in cloud environment[J].Advances in Engineering Software,2011,42(3):419-425.
[9] Buyya R,Murshed M M,Abramson D,et al.Scheduling parameter sweep applications on global grids:A deadline and budget constrained cost-time optimization algorithm[J].Software Practice and Experience,2005,35(5):491-512.
[10] Blanco C V,Huedo E,Montero R S,et al.Dynamic provision of computing resources from grid infrastructures and cloud providers[C]∥Proc of Grid and Pervasive Computing Conference,2009:113-120.
[11] Topcuoglu H,Hariri S,Wu M Y.Performance-effective and low complexity task scheduling for heterogeneous computing[J].IEEE Transactions on Parallel and Distributed Systems,2002,13(3):260-274.
[12] Mezmaz M,Melab N,Kessaci Y,et al.A parallel bi-objective hybrid metaheuristic for energy-aware scheduling for cloud computing systems[J].Journal of Parallel and Distributed Computing,2011,71(10):1497-1508.
[13] Dogan A,Ozguner F.Reliable matching and scheduling of precedence constrained tasks in heterogeneous distributed computing[C]∥Proc of the 29th International Conference on Parallel Processing,2000:307-314.
[14] Dogan A,Ozguner F.Matching and scheduling algorithms for minimizing execution time and failure probability of applications in heterogeneous computing[J].IEEE Transactions on Parallel and Distributed Systems,2002,13(3),308-323.
[15] Dai Yuan-sun,Xie Min.Reliability of grid service systems[J].Computers and Industrial Engineering,2006,50(1/2):130-147.
[16] Levitin G ,Dai Yuan-sun.Service reliability and performance in grid system with star topology[J].Reliability Engineering and System Safety,2007,92(1):40-46.
[17] Foster I,Zhao Y,Raicu I,et al.Cloud computing and grid computing 360-degree compared[J].IEEE Grid Computing Environments(GCE 2008),2008:1.
[18] Blaze M,Feigenbaum J,Lucy J.Decentralized trust management[C]∥Proc of the IEEE Computer Society Symposium on Research in Security and Privacy,1996:164-173.
[19] Josang A.Trust-based decision making for electronic transactions[C]∥Proc of the 4th Nordic Workshop on Secure Computer Systems(NORDSEC’99),1999:1.
[20] Josang A.A logic for uncertain probabilities[J].International Journal of Uncertainty,Fuzziness and Knowledge-Based Systems,2001,9(3):279-311.
[21] Wang W,Zeng G S,Yuan L L.A reputation multi-agent system in semantic web[C]∥Proc of the 9th Pacific Rim International Workshop on Multi-Agents,2006:211-219.
[22] Wang W,Zeng G S,Tang D Z,et al.Cloud-DLS:Dynamic trusted scheduling for cloud computing[J].Expert Systems with Applications,2012,39(5):2321-2329.
[23] Mui L,Mohtashemi M,Halberstadt M.A computational model of trust and reputation[C]∥Proc of the 35th Hawaii International Conference on System Sciences,2002:1.
[24] Thomas L,John S J.Bayesian methods:An analysis of statisticians and interdisciplinary[M].New York:Cambridge University Press,1999.
[25] Jameel H,Hung L X,Kalim U,et al.A trust model for ubiquitous systems based on vectors of trust values[C]∥Proc of the 7th IEEE International Symposium on Multimedia,2005:674-679.
[26] Shi Jin-qiao,Cheng Xiao-ming.Research on penalty mechanism against selfish behaviors in anonymous communication system[J].Journal on Communication,2006,27(2):80-86.(in Chinese)
[27] Josang A,Ismail R.The beta reputation system[C]∥Proc of the Bled Conference on Electronic Commerce,2002:1.
[28] Sih G C,Lee E A.A compile-time scheduling heuristic for interconnection-constraint heterogeneous processor architectures[J].IEEE Transactions on Parallel and Distributed Systems,1993,4(2):175-187.
[29] Peterson L,Bavier A,Fiuczynski M,et al.Towards a comprehensive PlanetLab architecture[R].Technical Report PDN-05-030.New Jersey:PlanetLab Consortium,2005.
[30] Calheiros R N,Ranjan R,De Rose C A F,et al.CloudSim:A novel framework for modeling and simulation of cloud computing infrastructures and services[R].Technical Report GRIDS-TR-2009-1.Australia:Grid Computing and Distributed Systems Laboratory,The University of Melbourne,2009.
附中文参考文献:
[26] 时金桥,程晓明.匿名通信系统中自私行为的惩罚机制研究[J].通信学报,2006,27(2):80-86.

