基于DSP+FPGA 的LFMCW 雷达测距信号处理系统设计*

陈林军，涂亚庆，刘 鹏，沈艳林

(后勤工程学院 后勤信息与军事物流工程系，重庆401311)

0 引 言

线性调频连续波(linear frequency modulated continuous wave，LFMCW)雷达测距系统具有精度高、适用范围广、工作电压低和安全性高等优点，在化工、冶金和油气储运行业有广泛应用［1］。在理论研究方面，LFMCW 雷达测距问题实质是中频信号的频率估计问题，文献［2 ～6］提出了多种高精度频率估计方法，由于实验条件限制，目前很多计算复杂的方法只实现了离线验证。在信号处理系统方面，雷达测距系统一般采用基于单片机、数字信号处理器(DSP)或现场可编程门阵列(FPGA)的方案。但是，单片机的软硬件资源有限，难以实现复杂算法［7］;DSP 具有很强的浮点运算能力，但不能够并行运行程序且外设驱动能力不如FPGA［8］;FPGA 外设驱动能力强，资源丰富，且程序高速并行运行，但是其实现浮点运算相当复杂［2］，给测距算法的嵌入增加了难度。

本文充分利用DSP 和FPGA 各自的优势，设计了基于DSP+FPGA 的LFMCW 雷达测距信号处理系统，实验验证表明:系统能够满足所提方法对硬件资源的需求，为高精度频率估计方法提供了在线实验验证手段，为实现高精度连续雷达波测距系统打下了坚实基础。

1 LFMCW 雷达测距原理及其信号处理系统方案

LFMCW 雷达测距原理为:信号处理系统输出调制电压，驱动VCO(压控振荡器)产生线性调频的正弦信号作为天线发射信号，发射信号和回波信号经过混频器处理后得到中频信号，测量中频信号的频率进而得到距离信息。

信号处理系统是LFMCW 雷达测距装置的核心，其设计方案如图1 所示。系统以FPGA 和DSP 为核心，FPGA主要负责A/D 转换器、D/A 转换器和LCD 的控制，DSP 主要用于实现测距的数字信号处理算法和系统与上位机的通信。

图1 信号处理系统硬件结构Fig 1 Hardware structure of signal processing system

电源模块为整个信号处理系统供电，表1 列出了设计中使用的主要芯片的型号及其供电要求。表1 中包含5 种幅度的直流电压，此外，D/A 转换电路后的运放电路供电为9 V，因此，电源模块采用9 V 电源供电，通过电源芯片降压后得到其它芯片的供电电压。

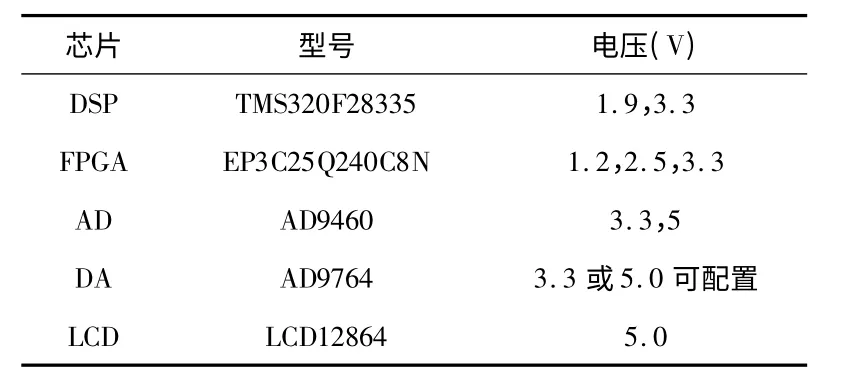
表1 主要芯片型号Tab 1 Types of main chips

2 FPGA 控制模块设计

信号处理系统的FPGA 控制模块主要分为三个部分:数据采集模块、调制波形产生模块和结果显示模块，图2 是整个FPGA 控制模块的块状图(引脚略)。

图2 中共有3 个不同时钟信号，分别是A/D 转换时钟clk_ad，D/A 转换时钟clk_da 和FPGA 内部逻辑时钟clk，它们都是通过FPGA 内部锁相环分频得到。

2.1 数据采集模块

数据采集模块主要器件是A/D 转换器，其工作过程由时钟信号进行控制，AD 从时钟信号有效到输出转换结果要经过13 个时钟周期的延迟，每个时钟周期输出一个16 位的数据，FPGA 通过通用IO 口采集AD 的输出结果。

数据采集模块实现的是存储A/D 转换结果并将数据传送给DSP 进行处理的功能。如图2(a)所示，该模块主要由一个异步FIFO 和一个FIFO 控制逻辑构成。数据从AD 到FIFO 的传输过程由FIFO 控制逻辑进行控制，而数据从FIFO 到DSP 的传输过程则由DSP 的读操作进行控制。

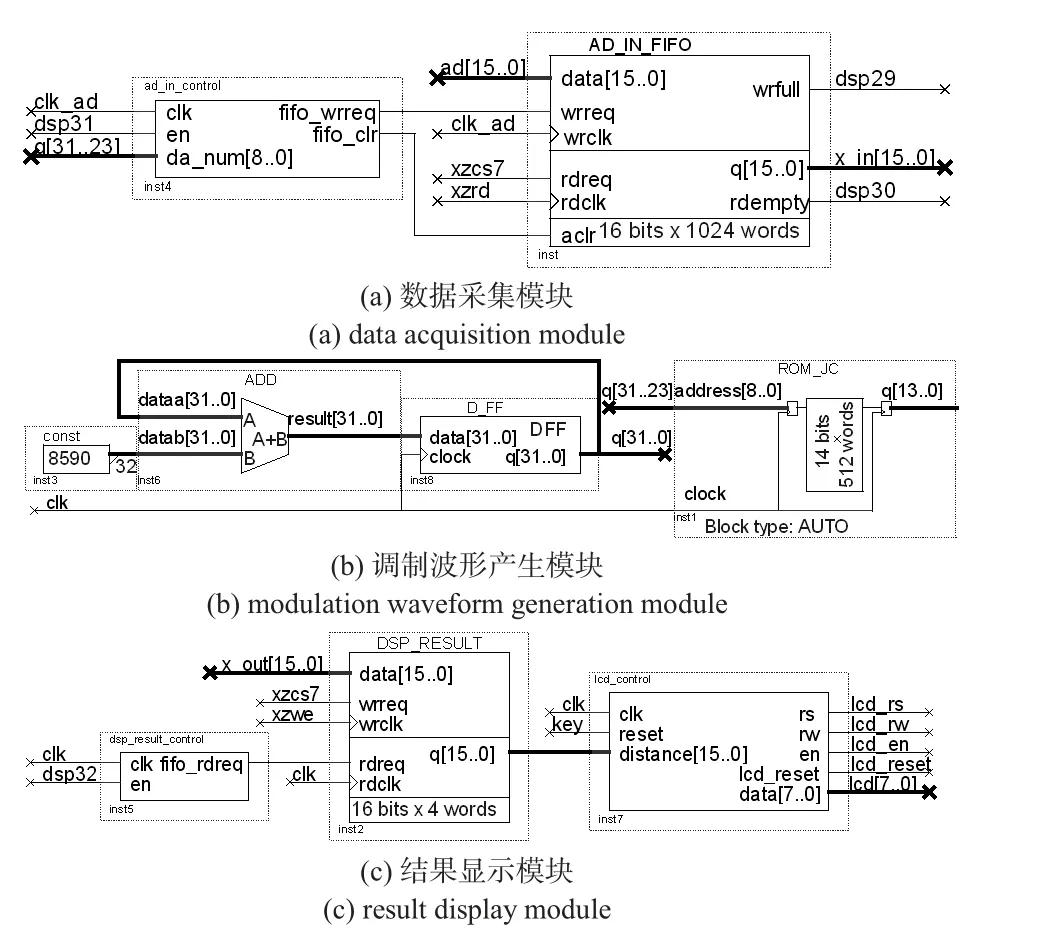
图2 FPGA 控制模块块状图Fig 2 Block diagram of FPGA control module

2.2 调制信号产生模块

调制信号产生模块实现数字频率合成器(DDS)功能，即生成并输出数字锯齿波信号，利用D/A 转换器将数字锯齿波信号转换成模拟锯齿波信号，经过放大滤波后作为VCO 的输入扫频电压。

如图2(b)所示，该模块主要由三个部分组成:累加器、D 触发器和ROM 存储器。累加器输入的常数值决定累加器的溢出周期T，其计算公式如式(1)所示

其中，N，fda，C 分别为累加器的数据宽度，clk_da 的频率和累加常数值。该模块的ROM 存储器中保存的是一个周期的锯齿波波形，由于VCO 调频存在非线性，使用经过非线性校正后的波形能够有效减小调频非线性对雷达测距精度的影响。

2.3 结果显示模块

结果显示模块实现结果可视化功能，该模块接收DSP处理得到的距离信息并将距离信息输出显示到LCD 屏。如图2(c)所示，结果显示模块有三部分组成:FIFO 控制逻辑、异步FIFO 和LCD 控制逻辑。与数据采集模块中的FIFO 控制逻辑相似，结果显示模块中的FIFO 控制逻辑也起着协调DSP 和FIFO 的作用。当DSP 处理完采样信号，得到距离信息后，DSP 对FIFO 进行写操作，数据传输完毕后，FIFO 控制逻辑将FIFO 读使能置1，数据由FIFO 读出到LCD 控制逻辑。LCD 通过内部逻辑逐位将距离信息显示到LCD 屏。

3 DSP 程序设计

3.1 程序流程

DSP 是信号处理的核心，主要实现数据的读取、处理和输出功能。DSP 程序流程如图3 所示，主要分为系统初始化、双核通信、信号处理算法实现和结果输出等环节，其中，双核通信和信号处理算法实现环节在中断程序中实现。

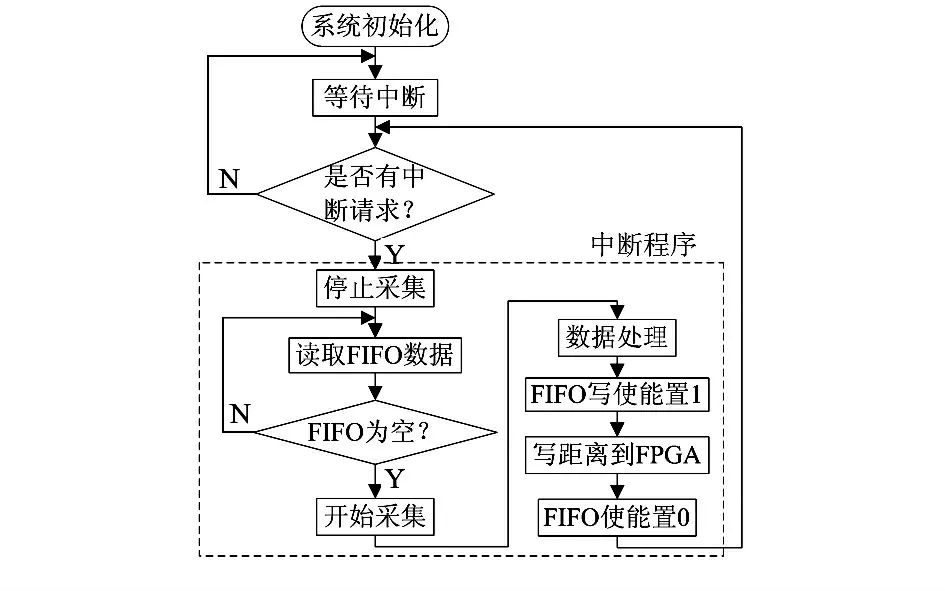
图3 DSP 程序流程Fig 3 Flow chart of DSP program

系统开始工作后，首先进行系统初始化，然后系统等待触发中断程序。在中断程序中，DSP 完成与FPGA 的通信和信号处理。DSP 收到FPGA 发出的读取数据的中断请求后，控制FPGA 停止缓存数据并通过XINTF 外部接口读取FPGA 内部FIFO 缓存的数据，数据读取完毕后控制FPGA 继续缓存;然后DSP 通过嵌入的信号处理算法计算出距离信息，最后将距离信息写入到FPGA 的FIFO 中，同时，也可以通过RS—232 将距离信息发送到上位机进行显示。

3.2 算法实现

本文采用基于相位匹配法的测距算法，该算法理论精度高，误差接近克拉美罗下限(CRLB)。该算法的核心是利用相位匹配法估计角频率ω，如式(2)所示［6］

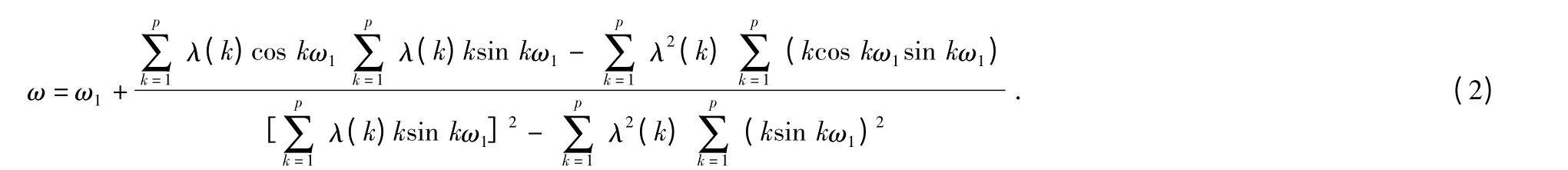
其中，λ 和ω 分别表示自相关信号、自相关信号长度和利用PHD 法［9，10］计算自相关信号角频率。

基于相位匹配法的测距算法中运用了大量的加法和乘法运算，其中包含很多重复计算，例如:k 每变化一次，kω1需计算6 次，cos kω1计算2 次，sin kω1计算4 次。为提高运算速度，尽量减少重复计算，本文采用中间变量保存kω1，cos kω1和sin kω1的计算结果。在存储空间分配上，由于只有计算λ(k)时会调用原始采样数据，因此，将cos kω1和sin kω1的结果保存在原始采样数据所在的存储空间。

4 实验验证与分析

为验证信号处理系统的效果，设计了利用信号发生器的加噪正弦信号模拟雷达中频信号的实验，调制波形通过示波器进行观察测量。

实验中，设置N=32，fda=50 MHz，C=8 590，通过示波器观察调制电压的输出，得到周期为10 ms 的稳定锯齿波。由此可知，调制信号产生模块设计正确，工作正常。在雷达系统应用中，可以根据不同的VCO 的电调特性改变ROM中的波形数据，与不同的雷达前端配套使用。

设实验模拟的雷达前端的调频带宽为1 GHz，调频周期为10 ms，噪声电平设置为50%(可调节的最大值，其对应SNR=13.86 dB)，则实验中信号发生器输出的5 组正弦波的参数及其对应的理论距离和实测距离如表2 所示，其中实测距离为5 次测量的平均值。

由表2 可知，本文设计的信号处理系统能够实现中频信号采集、数据处理和结果显示的功能，说明数据采集模块、结果显示模块和信号处理系统硬件和软件设计正确。对于信号发生器产生的加噪单频正弦信号模拟测距实验，测量精度达到了1 mm，验证了基于相位匹配法的测距算法的测距效果。

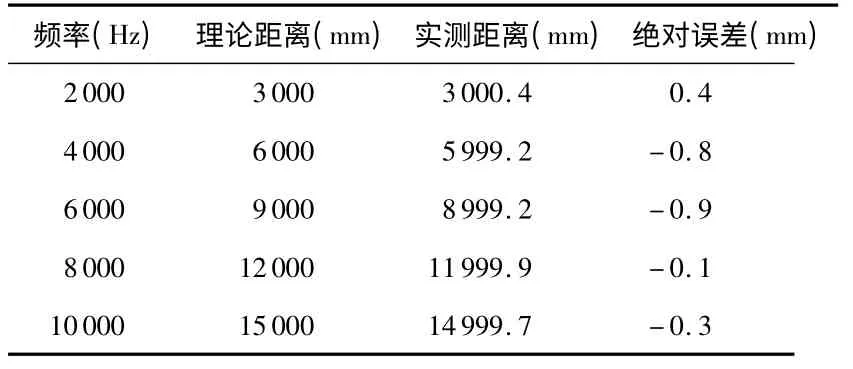
表2 实验结果Tab 2 Experimental results

5 结 论

本文设计了以DSP+FPGA 双核架构的雷达信号处理系统，完成了硬件系统的搭建和软件系统设计，实现了基于相位匹配法的测距方法，并进行了实验验证。

实验结果表明:基于DSP+FPGA 的LFMCW 雷达测距信号处理系统板上资源丰富，外设驱动能力强，能和多种不同雷达前端结合使用;运算能力强，适用于复杂测距算法验证且硬件对算法造成的精度损失小;相位匹配法用于测距精度高且便于在DSP+FPGA 架构的信号处理系统中实现。

［1］ 刘良兵.频率估计的信息融合方法及其应用［D］.重庆:后勤工程学院，2008:1－2.

［2］ 詹启东，涂亚庆.基于Rife 法的线性调频连续波雷达测距算法及实现［J］.兵工学报，2014，35(5):748－752.

［3］ 肖 玮，涂亚庆，刘良兵，等.频率估计的多段差频正弦信号加权融合算法［J］.中国科学技术大学学报，2012，42(2):124－132.

［4］ 苏 丹，涂亚庆，沈艳林，等.异频信号的交叉信息融合频率估计方法［J］.仪器仪表学报，2014，35(1):15－22.

［5］ 苏 丹，涂亚庆，罗健源，等.基于迭代的交叉信息融合频率估计方法［J］.四川大学学报:工程科学版，2013，45(4):156－162.

［6］ Shen Y L，Tu Y Q，Chen L J，et al.A phase match－based frequency estimation method for sinusoidal signals［J］.Review of Scientific Instruments，2015，86(4):045101.

［7］ 岳文豹，杨 录，张艳花.FMCW 雷达近程测距系统设计［J］.电子技术应用，2012，38(4):73－75.

［8］ 唐慧强，赵长超，薛 莉.无线FMCW 雷达测距系统的设计［J］.测控技术，2014，33(1):55－58.

［9］ Pisarenko V F.The retrieval of harmonics from a covariance function［J］.Geophysical Journal of the Royal Astronomical Society，1973，33(3):347－366.

［10］Lui K W K，So H.Modified pisarenko harmonic decomposition for single－tone frequency estimation［J］.IEEE Transactions on Signal Processing，2008，56(7):3351－3356.