基于相位生成载波的全光纤传感器定位研究*

许海燕，吴红艳，肖 倩

(1.复旦大学，上海200433;2 河海大学 物联网工程学院，江苏 常州213022)

0 引 言

光纤传感技术是伴随着光纤通信的发展而迅速发展起来的，其中，由于光纤分布式振动测量技术可实现线状的、长距离大范围的实时、连续监测，分布式振动传感技术成为近年来研究的热点技术之一。分布式光纤传感器已被广泛应用于周界安防、油气及电力线路安全保障等领域，为经济的发展和社会的稳定提供了保障［1，2］。

基于迈克尔逊干涉仪的全光纤振动传感器对外界振动信号的定位原理是通过“陷波点”的频率来确定振动点位置［3～5］。用这种方法进行定位时得到的信号频谱，其陷波点位置不清晰，且阶数较少，原因在于光纤结构存在缺陷，造成光在光纤中传输时会发生瑞利散射，产生的回光干涉信号的频谱与通过法拉第旋转镜反射的光干涉得到的频谱发生叠加，由此造成信号频谱陷波点的不清晰，影响定位的精度。

本文通过在传感臂的末端加入相位调制器，进行相位调制，能够消除频谱的叠加，提高定位的精度。

1 结构与原理

1.1 系统结构

干涉型光纤传感器的原理是:根据光弹效应，当外界振动信号作用在光纤上时，光纤长度和折射率等发生变化，光程变化导致光相位变化［6，7］。通过构造光路使两路相干光干涉，从干涉光强中就能得到光相位变化的信息，即外界振动信号的信息。干涉型光纤传感器主要应用的是迈克尔逊(Michelson)干涉仪、马赫—曾德尔(Mach-Zenhder)干涉仪、Sagnac 干涉仪以及各干涉仪之间混合组成的干涉系统。本文构造了一个基于迈克尔逊干涉仪的全光纤振动传感系统，其基本结构如图1 所示。

图1 相位调制器的分布式光纤传感器Fig 1 Distributed optical fiber sensor with phase modulator

图1 中，波长为1 310 nm 的超辐射二极管SLD 发出的光经过3×3 耦合器DC1 产生初始相位差为的两束相干光，分别经过光路IP1:1—3—4—5—6—5—4—3—2 和光路IP2:2—3—4—5—6—5—4—3—1，在耦合器DC1 内部发生干涉，输出两路干涉信号至光电二极管PIN1 和PIN2。其中，DC2 为2×2 耦合器，C 为长度数公里的延时线圈，4 处为外界扰动点，5 为相位调制器，6 为法拉第旋转镜。

根据文献［3，4］，通过PIN1 和PIN2 检测到的干涉信号可以解调出随扰动信号线性变化的相位信号，该信号的频谱有凹陷点，称为“陷波点”。陷波点频率f(k)与扰动点距法拉第旋转镜间的距离L 之间满足为

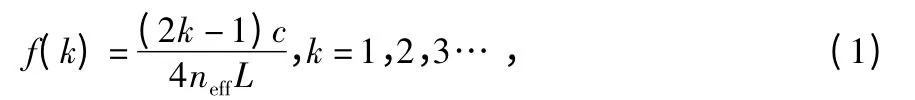
式中 k 为第k 阶陷波点，c 为真空中的光速，neff为光纤的有效折射率。由于光在光纤中传播时会发生瑞利散射形成回光［7，8］，假设发生散射的位置与扰动点的距离为L1，则两路回光经过干涉得到的信号频谱会产生另一组陷波点

因为光在光纤中发生散射的位置无法确定，所以，通过这组陷波点无法定位扰动点的位置，而这组陷波点的存在会影响到有效陷波点f(k)的检测。图1 所示的系统，将相位调制器放置在末端，并且在相位调制器上加高频的调制信号，使得只有到达传感臂末端的光会被相位调制，产生高频的相位变化，因此，经过耦合器干涉后的信号集中在高频;散射产生的回光不会被调制，未被调制的光干涉后信号的频谱集中在低频。这样可以用高通滤波器将低频信号滤除，消除其对陷波点检测的影响。

1.2 相位载波解调原理

在相位调制器上加载调制幅度为φ0，角频率为ω0的载波时，光电二极管获得的光强信号可以表示为［9］

式(3)、式(4)中包含外界振动信号产生的相位差φs(t)，为了获得用于定位的信号φs(t)，采用以下解调的方法。

将式(3)用第一类贝塞尔函数展开得［7］

式中 Jk为第一类k 阶贝塞尔函数。式(5)中含有ω0的各次倍频项，将式(5)乘以cos ω0t 后进行低通滤波，滤除ω0及其各次倍频，即可得到

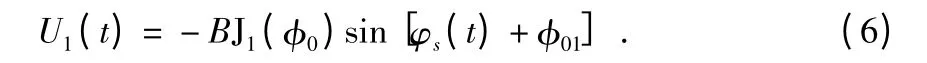
对式子(4)表示的信号做同样的处理可得到

上式积分并经过高通滤波器后得

式中 V(t)为与外界扰动信号呈正比的信号，从V(t)信号的频谱可以得到与扰动点位置相关的陷波点频率。

2 实验结果与实验分析

2.1 不加相位载波进行定位

在法拉第旋转镜前不加相位调制器时，PIN1 和PIN2接收到的干涉光强可以表示为

取传感臂(图1 中3 ～5 之间)的长度为30.3 km，在传感臂的起始位置(3 处)用较大的力弹光纤。PIN1 和PIN2获得的信号I1(t)和I2(t)如图2(a)，(b)所示;I1(t)和I2(t)经过相位解调可以获得与扰动信号呈正比的信号φs(t)，如图2(b)所示;用Welch 法对信号φs(t)作频谱估计，得到的频谱如图2(c)所示。

扰动点位置与陷波点频率的关系为

式中 光纤等效折射率neff≈1.5，c 为光在真空中的速度。

φs(t)的频谱上有3 个陷波点，它们的频率以及代入式(12)计算得到的相应的扰动点位置如表1 所示。

图2 无相位载波的定位结果，实际扰动点位置L=30.3 kmFig 2 Positioning result without phase carrier involved，while real L=30.3 km

表1 陷波点频率和定位结果Tab 1 Frequency of trapped waves point and positioning result

扰动点位置为L=29.679 km，均方误差为δ=8.554，定位的绝对误差为621 m，相对误差为2%。

2.2 加相位生成载波进行定位

在相位调制器上加频率为176.3 kHz，幅度3.5 V 的电信号，进行相位载波调制。在传感臂的起始位置(3 处)弹光纤。PIN1 和PIN2 获得的信号与载波混频并滤波后得到式(6)、式(7)表示的信号U1(t)和U2(t)，设置采集卡的采样率400 kHz，得到的信号分别如图3(a)，(b)所示;将图3(a)，(b)中的两路信号微分并与交叉相乘后相减得到的信号(t)经过积分和高通滤波器可得与外界扰动呈正比的信号V(t)，如图3(c)所示。信号V(t)用Welch 法进行频谱估计，其频谱如图3(d)所示。

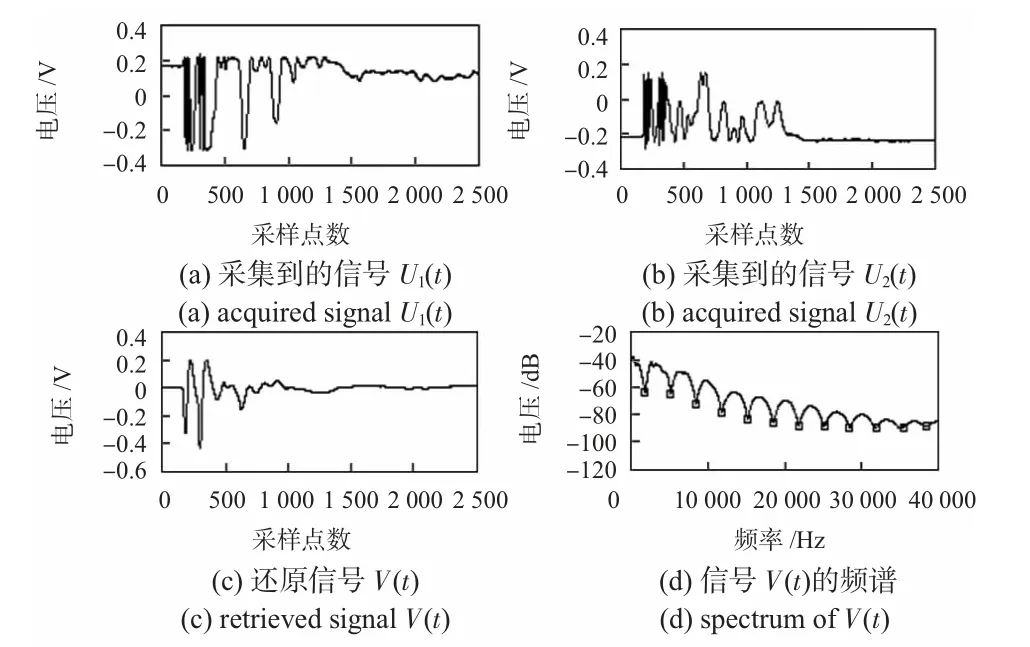
图3 加相位载波的定位结果，实际扰动点位置L=30.3 kmFig 3 Positioning result with phase carrier，while real L=30.3 km

从图3(d)所示的频谱中得到的陷波点的频率位置和代入式(12)计算得到的扰动点位置如表2 所示。

表2 陷波点频率和定位结果Tab 2 Frequency of trapped waves point and positioning result

3 结 论

实验结果显示:采用在法拉第旋转镜前加相位调制器进行相位载波调制的方法可以有效地增加陷波点的级数，并且使陷波点清晰，陷波点的位置能够准确估计，利用各级陷波点计算出的扰动点位置准确性高，最大定位误差在50 m内。这种方法在光路上只需要在原有反射头前接入一个相位调制器进行调制，电路上加两个乘法器和两个滤波器进行解调即可，易于实现，且能够大大提高定位的精度。

［1］ He Z Y，Hotate K.Distributed fiber-optic stress-location measurement by arbitrary shaping of optical coherence function［J］.Journal of Lightwave Technology，2002，20(9):1715－1723.

［2］ Culshaw B，ersey A.Fiber-optic sensing:A historical perspective［J］.Journal of Lightwave Technology，2008，26(9):1064－1078.

［3］ 尹崇博，贾 波，肖 倩，等.分布式光纤传感器触发模式识别的研究［J］.传感器与微系统，2008，27(7):15－20.

［4］ 吴红艳，贾 波，叶 佳.基于光纤干涉定位系统的信号解调技术［J］.传感器与微系统，2007，26(5):45－47.

［5］ 贾 波，钱松荣，华中一，等.全光纤干涉系统用于光纤长度测量实验［J］.光电子激光，2002，29(1):73－75.

［6］ 邢进华，钱 斌，冯金福.用光纤白光干涉技术测量晶体的弹光系数［J］.光子学报，2007，36(5):890－893.

［7］ 张 悦，张记龙，李 晓，等.光纤中拉曼散射回波超高灵敏度探测技术研究［J］.光谱学与光谱分析，2009，29(5):1300－1303.

［8］ 任国斌，王 智，娄淑琴，等.单模光纤的瑞利散射损耗研究［J］.铁道学报，2003，25(5):61－63.

［9］ 王泽锋，胡永明，孟 洲，等.干涉型光纤水听器相位载波调制—解调中信号混叠产生的机理及解决方案［J］.光学学报，2008，28(1):92－98.