15 kW 开关磁阻电机调速系统仿真与测试

徐新明 卞永明 杨 濛 戴松贵

(同济大学机械与能源工程学院1，上海 201804;上海同新机电控制技术有限公司2，上海 200949)

0 引言

近年来，电力驱动技术得到了飞速的发展并且已经在工业和电动汽车领域得到了成功应用［1］。电力驱动系统是由发电机或者电池向电动机供电，电动机驱动负载，将电能转换成运动的动能。电力驱动系统中使用的驱动电机主要有直流电机、感应电机与永磁同步电机［2］。开关磁阻电机(switched reluctance motor，SRM)由于结构简单、成本低，启动转矩大，调速范围广，可在极高的转速下工作，能适应高温和强振动的工作环境，其在电力驱动系统应用中得到越来越多的关注。相对于其他电机，SRM 结构简单，功率转换电路效率高，这使得SRM 能够代替电力驱动系统中的其他电机。

本文以15 kW 的SRM 为研究对象，分析SRM 的运行原理与数学模型，在Simulink 中建立开关磁阻调速系统(switched reluctance motor drive，SRD)的仿真模型，对系统的转速响应、转矩响应进行仿真;设计搭建了系统的试验台架，对电机进行静态和动态试验，测试电机的特性测试曲线、效率以及电机在低速状态下转矩的波动［3-4］。

1 SRM 系统原理

1.1 SRM 结构与运行原理

从结构上来讲，SRM 是一种同步电机，也是最简单的电机。它只是定子上有线圈绕组，转子是由简单的硅钢片压制而成，没有线圈或永磁铁。由于其定子、转子均为凸极式构造，因此又称双凸极结构。不同结构的SRM 只有相数以及转子极数、定子极数上的区别。

最基本的三相SRM 定子有6 极，转子有4 级，称为6/4 结构。将定子和转子的极数同时增加一倍，即可得到12/8 结构的SRM;如增加两倍，则可得到24/16 结构的SRM。最基本的四相SRM 定子有8 极，转子有6 极，称为8/6 结构。若将定子和转子的极数同时增加一倍，即得到了16/12 结构的SRM。其他SRM还包括4/2、6/2、10/4、12/10 等结构。正是这种简单的构造使得SRM 有着低成本的优势［5］。

SRM 运行过程中转矩具有磁阻性质，其运行原理遵循“磁阻最小原理”［6］——磁通总是要沿磁阻最小的路径闭合，因磁场扭曲而产生切向磁拉力。当转子凸极与定子凸极错位时，气隙大、磁阻大;一旦定子磁极绕组通电，就会形成对转子凸极的磁拉力，使气隙变小——磁路磁阻变小。与此同时，用驱动开关按一定逻辑关系切换定子磁极绕组的通电顺序，即可形成连续旋转的力矩［7］。SRM 的运行是由电机转子位置传感器、功率变换器和控制器共同配合实现的，具体运行过程如图1 所示。

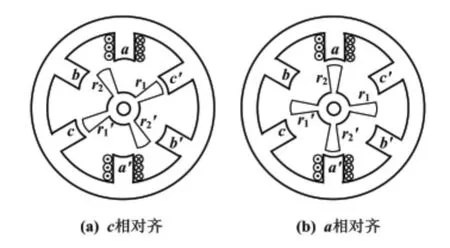
图1 6/4 结构SRM 运行原理Fig.1 The operating principle of SRM

当转子的r1和r1'极分别与定子的c'和c 极对齐，在定子a 相通入图1(a)中所示方向直流时，a 相绕组产生磁通，磁通从定子的a'极经过空气扭曲进入转子r2'极，再由转子r2极扭曲经过空气进入定子a 极，最后通过定子外圈闭合。因为a 极与r2极、a'极和r2'极分别错位，气隙大，磁阻不是最小，扭曲的磁场将分别产生a 极对r2极、a'极对r2'极的拉力，进而使得转子顺时针方向旋转。当a 极与r2极、a'极与r2'极对齐，a 相绕组断电，b 相绕组通电，如图1(b)，定子的b 极将分别吸引转子r1、r1'极，使转子继续沿顺时针转动。同样当c 相绕组通电后，将使转子的r1和r1'极分别与定子的c'和c 极对齐，完成转子旋转一周。如果改变a、b、c 三相的通电顺序，电机的转子将反向旋转，跟电流的方向无关［8］。

1.2 SRM 数学模型

SRM 运行原理虽然看似简单，但是其内部的电磁关系和运行特性都非常复杂，电流、电感及磁通呈非线性变化。通过线性化SRM 的模型之后，得到单相绕组的瞬时电压方程为:

式中:u 为绕组两端电压;i 为绕组电流;Rm为绕组的电阻;φ 为绕组产生的磁通。

由于SRM 的双凸极结构和磁场饱和因素的影响，绕组磁通φ 是绕组电流i 和转子旋转角度θ 和的函数。因此式(1)可以表示为:

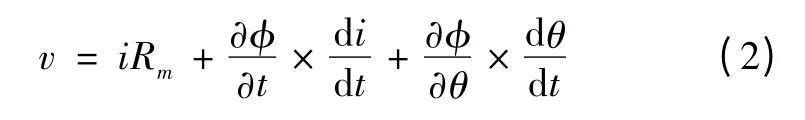
当正常运行时，SRM 的输出转矩取决了外部负载的大小，转子的运动机械方程表示为:

式中:Te为电机输出转矩;J 为系统转动惯量;w 为机械角速度;KΩ为摩擦系数;TL为负载转矩。

SRM 单相绕组瞬时输出转矩表示为:

式中:Wc为单相绕组的磁共能。SRM 输出转矩是随绕组线圈磁通量而变化，其大小与绕组线圈电流的平方成正比。

2 系统仿真

在Matlab/Simulink 环境下，建立以转速和电流为反馈的电压型PWM 双反馈SRD 系统模型［9-10］。SRD系统的功率电路采用三相不对称半桥式功率变换器结构，每相结构中包括两个IGBT 功率管和两个续流二极管。在导通期间，下桥臂IGBT 常开，上桥臂在PWM信号驱动下导通和关闭，以调节加在此相绕组上的正电压，实现调速。在上下IGBT 功率管都关断时，绕组两段形成负电压，绕组电流通过二极管续流，将能量返回到电源。转子的位置由位置检测模块测量得到，根据转子的位置，通过调节相绕组的导通角和关断角来控制扭矩的产生。

2.1 转速响应仿真

在空载、100 Nm 负载状态下，分别将电机调至额定转速1 500 r/min进行仿真，仿真结果如图2 所示。在空载下状态电机转速很快从0 达到目标转速，上升时间小于1 s，转速有小量的超调，响应迅速，如图2(a)所示。

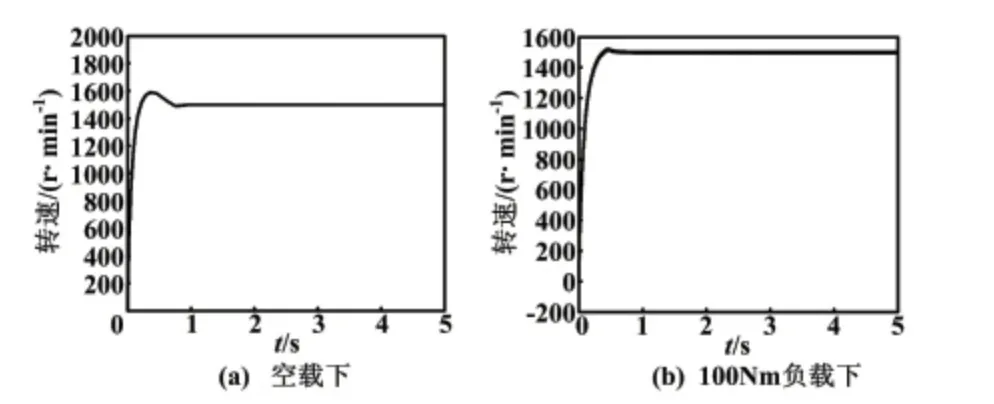
图2 转速阶跃响应曲线Fig.2 Step response curves of rotational speed

在电机额定转矩100 Nm 负载条件下，将电机转速调至额定转速1 500 r/min。电机在1 s 内迅速达到目标转速，且从转速响应的放大图中可以发现，电机转速波动范围很小，最大值1 502.5 r/min，最小值1 498 r/min，波动幅度0.1%，如图2(b)所示。

图3 为空载和负载50 Nm 状态下的转速方波阶跃响应图。转速在阶跃上升或者是阶跃下降都在1 s 内完成达到稳定，转速在阶跃上升的过程中，空载状态下有一部分转速的超调，而负载状态下无超调。

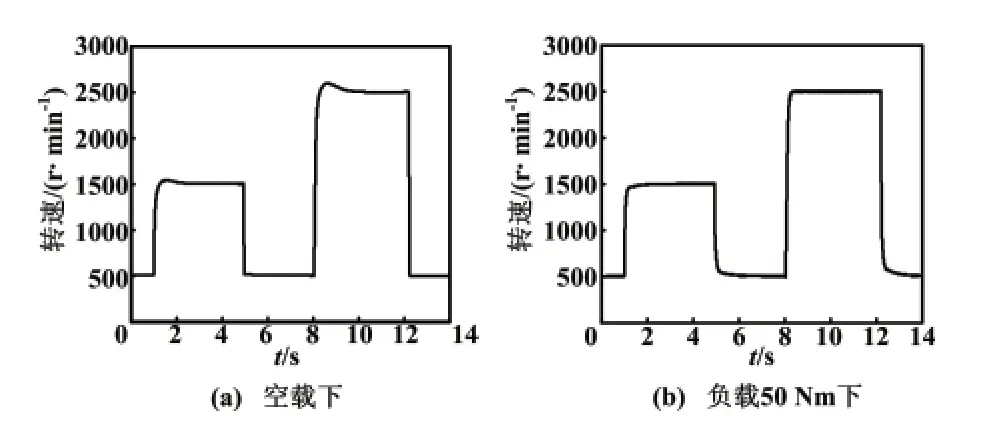
图3 转速方波响应曲线Fig.3 Square wave response curves of rotational speed

2.2 转距响应仿真

将电机转速调至额定转速与1/2 额定转速，在两种转速下驱动电机转矩方波加载，分别得到电机在转速1 500 r/min 和800 r/min 下转矩方波的响应结果如图4 所示。

图4 转矩方波响应曲线Fig.4 Square wave response curves of torque

当负载从低到高阶跃时，由于电机输出的功率不能阶跃，电机输出的功率变换需要一定的时间来转变，故负载的陡增会造成电机转速的急剧下降。当控制器检测到转速误差时，调节输出电压，直至恢复负载阶跃之前的转速状态。电机转速的急剧下降幅度与负载阶跃的大小有关，负载阶跃越大，转速下降越大。同理当负载阶跃下降时，瞬时的输出功率不变，导致转速急剧上升，直至控制器调节输出功率来降低输出的转速。同时仿真结果也表明，无论是转矩的阶跃增大或是阶跃减小，都会引起电机转速的急剧变化，但是在短时间内系统又会达到平衡状态，说明电机对转矩的阶跃响应优秀。

3 系统台架测试

整个电机系统试验台架主要由SRM、转速转矩传感器、液压泵、联轴器、负载溢流阀台架底座及相应的安装机架组成［11］。测试的对象为15 kW 的SRM，额定转速1 500 r/min，额定转矩100 Nm，测试将对电机的静态性能与动态性能进行分别测试。

3.1 电机静态测试

(1)特性测试。

将电机转速设置为多个转速点。通过调节溢流阀的压力来调节每个转速下电机的负载大小，测试电机在各个转速点下可以输出的最大转矩。测试过程中，SRM 能够输出的最大稳定转矩则是电机的有效最大输出转速，工作点稳定时间不少于20 s。

通过测量，得到如图5 所示的转速、转矩、电流与效率之间的变化关系。由测量结果可以看出电机的最大效率达到88%，电机除了运行在500 r/min 时效率稍低，在其他转速下效率都超过了80%。

图5 电机测试数据图Fig.5 The motor test data

(2)低速下转矩波动测试。

将SRM 转速低于1 000 r/min 以下定为低速，分别测试1 000、800、500 与300(单位:r/min)转速下转矩的波动情况。测试结果如图6、图7 所示。

低速试验结果表明，SRM 在低速时，转矩脉动较大，且转速越低，脉动越大。在负载转矩100 Nm 下，转矩波动幅度的最大值为3%，发生在最低转速300 r/min时。在负载转矩为50 Nm 下，转矩波动幅度的最大值达到10%，发生在转速300 r/min 时。同时，当转速相同时，负载转矩越大，电机输出的转矩波动幅度反而越小。不同转速下的转矩波动情况如表1所示。

图6 转矩在100 Nm 时的波动情况Fig.6 Torque ripple at 100 Nm

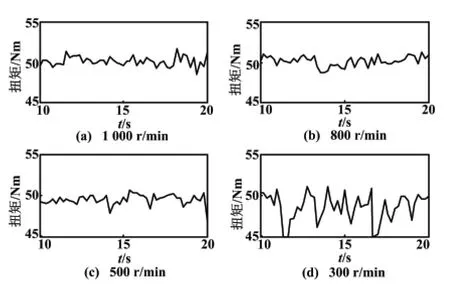
图7 转矩在50 Nm 时的波动情况Fig.7 Torque ripple at 50 Nm

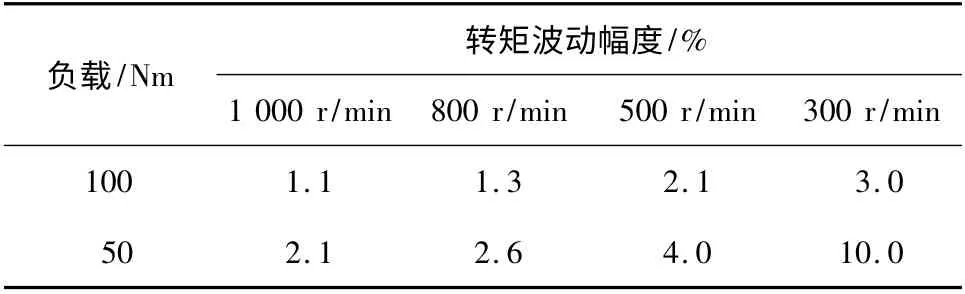
表1 转矩波动幅度Tab.1 The amplitude of torque ripple

3.2 电机动态测试

(1)空载下转速响应测试。

空载下转速响应曲线如图8 所示。在空载状态下，将SRM 分别设置转速至额定转速1 500 r/min 和最高转速3 000 r/min，电机转速响应曲线如图8(a)所示。电机从启动到目标转速不超过3 s，到达目标转速之后有小量超调，然后趋于稳定。此外，电机自由停车所需时间与停车之前转速有关，1 500 r/min 停车需要10 s，3 000 r/min 停车需要15 s，转速越高停车时间越长，这符合惯性定律。

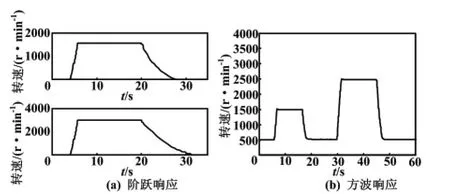
图8 空载下转速响应曲线Fig.8 Rotational speed response curves under unloading

图8(b)为电机在空载下转速方波响应曲线。电机在转速500→1 500→500→2 500(单位:r/min)转速阶跃过程中，转速响应迅速，上升时间和下降时间均不超过3 s，说明SRM 调速性能优秀。

(2)转矩方波响应测试。

转矩方波响应曲线如图9 所示。

图9 转矩方波响应曲线Fig.9 Square wave response curves of torque

图9(a)为转速1 500 r/min 时，50→100→50(单位:Nm)转矩方波响应曲线。图9(b)为在转速800 r/min 时，50→100→50(单位:Nm)转矩方波响应曲线。

表2 为转矩方波响应结果。

表2 转矩方波响应时间Tab.2 Torque step square wave response time

4 对比分析

4.1 仿真结果分析

SRD 系统空载时，电机从启动到达额定转速1 500 r/min，稳定时间小于1 s，响应迅速，转速最大值达到1 600 r/min，超调量大约7%。目标转速为3 000 r/min时，电机响应与在1 500 r/min 下特征基本相同;电机对转速的阶跃方波响应都在1 s 内完成并达到稳定。转速在阶跃上升的过程中，空载状态下有小量的转速超调，而负载状态下无超调;在额定负载、额定转速条件下，电机同样在1 s 内迅速达到目标转速。在电机转速稳定后，电机转速波动范围很小，最大值1 502. 5 r/min，最小值1 498 r/min，波动幅度0.1%。在额定负载下，电机的输出转矩波动较大，最大值101. 8 Nm，最小值98. 2 Nm，波动幅度达到1.8%。在转矩阶跃响应过程中，转矩的阶跃导致转速的急剧变化，电机转速在短时间内稳定，说明SRM 对转矩的变化响应优秀。

4.2 试验结果分析

电机在静态试验过程中，实际测试得到的驱动电机的转矩和功率外特性曲线与理想外特性曲线基本重合。整个系统的效率在其额定转速1 500 r/min 附近时效率最高，可以达到88%，其余转速下系统效率都大于80%，但是在转速为500 r/min 时效率低于80%。在低速状态下，电机的输出转矩波动较大，在300 r/min@50 Nm 的情况下，转矩波动达到10%，说明SRM 的低速确实不理想，所以实际使用中应该尽可能地避免在低速下工作。在电机的动态响应过程中，电机从启动到目标转速的上升时间小于3 s，在空载下有小幅超调，在负载状态下基本无超调。同时对转速阶跃响应迅速，响应时间均小于3 s，说明SRM 对转速的响应优秀。在转矩的阶跃响应过程中，负载转矩从100 Nm 阶跃至50 Nm 时，电机响应时间大约为1 s，负载转矩从50 Nm 阶跃至100 Nm 时，电机的响应时间为2.9 s@1 500 r/min、4.1 s@800 r/min。这说明电机转速高的情况下，电机的输出转速对外负载的变化响应快。

4.3 仿真与试验对比

(1)在电机转速响应过程中，电机的输出转速形态在仿真与试验中表现大致相同，只是在对转速响应的稳定时间与超调量有些差异，这是由仿真与实际电机控制系统中的控制参数的差异而导致的。仿真与试验中的转速响应超调量在空载过程中分别为7%和3%，负载状态下，仿真与试验的超调量都为0，说明负载对超调有抑制作用，具体比较如表3 所示。

(2)通过仿真与试验，综合SRM 对转矩阶跃的响应，可以得到在额定转速1 500 r/min 下电机的输出转速与转矩。仿真与试验中转速与转矩的对比结果如图10 所示。

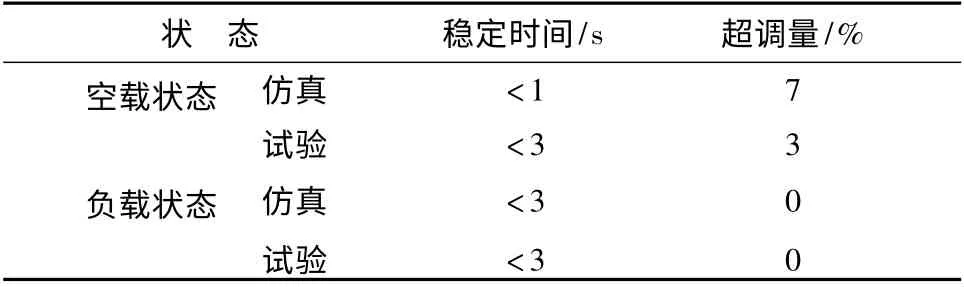
表3 转速响应仿真与试验结果对比Tab.3 The comparison between simulation and the test results of rotational speed response

图10 转速、转矩在仿真与试验中的对比结果Fig.10 The comparison between simulation and the test results of rotational speed and torque

当转矩阶跃变化时，会导致转速的急剧跳变。当转矩为阶跃上升时，仿真与试验时的转速分别跳跃至1 300 r/min 与1 400 r/min。当转矩为阶跃下降时，仿真与试验时的转速分别跳跃至1 600 r/min 与1 800 r/min。跳变的形态相同，说明仿真与试验结果的正确性，但跳变的幅度不同，这是由于试验中的转矩调节是通过控制负载液压阀的开关来实现的。仿真中的负载阶跃是理想的方波，而试验中用电磁阀控制负载转矩的变化，将阀芯位置从左位调节至右位有一定的响应时间，阀芯短暂地经过中位时，会产生近似零负载的状态，虽然时间非常短，但还是会反映到电机输出转矩与转速的变化上，因而导致试验中的转速跳跃幅度比仿真中的转速跳跃幅度大。此外可以发现试验中的转矩波动比仿真中的转矩波动大得多。究其原因为用液压泵作为负载，负载的大小与转速的平方成正比，微小的转速变化，便会产生较大的转矩变化，而转矩的变化又会反过来影响转速的变化，从而导致试验中的转矩波动较仿真中大。

5 结束语

利用Matlab/Simulink 搭建SRD 系统仿真模型，并对系统进行了转速与转矩响应仿真。搭建了SRD 系统的试验台架，对电机分别进行了静态和动态的试验，得到了电机的外特性测试曲线及效率曲线，并对装载机的运输工况和作业工况进行了模拟。仿真与试验结果逼近，误差较小，说明仿真模型真实反映了SRD 系统，具有实际的指导作用，也验证了SRD 系统控制策略的正确性。试验结果说明SRM 对转速、转矩响应性能优秀，SRM 的效率最高达到88%，发生在额定转速附近。仿真与台架试验结果都表明SRM 的转矩脉动较大，特别是低速300 r/min 时会超过10%。可以通过控制策略或者改变功率变换器的结构形式等方法来降低SRM 的转矩波动量。

［1］ Pantos M. Exploitation of electric-drive vehicles in electricity markets［J］.Power Systems IEEE Transactions on，2012，27:682-694.

［2］ Jin C，Zheng S，Tian H. Anti-drive system design and hierarchy control strategy of electric drive vehicle［J］. Transactions of the Chinese Society for Agricultural Machinery，2014，45(4):22-27.

［3］Guettaf A，Benchabane F，Bennis O，et al.Torque ripple minimization in switched reluctance motor using the fuzzy logic control technique［J］.International Journal of Systems Assurance Engineering＆ Management，2014(5):182-186.

［4］ Navardi M J，Babaghorbani B，Ketabi A. Efficiency improvement and torque ripple minimization of switched reluctance motor using FEM and seeker optimization algorithm［J］. Energy Conversion ＆Management，2014，78(2):237 -244.

［5］ Yun T H，Kim S J，Kim H J，et al. Switched reluctance motor:US，doi:US8633628 B2［P］.2014.

［6］ 刘旭，潘再平.煤矿输送机用开关磁阻电机驱动系统［J］. 煤炭学报，2009，34(2):280 -283.

［7］ 牟宏均.电动汽车所用牵引电机的性能简介及选择［J］.电脑知识与技术，2009，5(18):4921 -4923.

［8］ Krishnan R.Switched reluctance motor drives:modeling，simulation，analysis，design，and applications［M］.CRC Press，2001.

［9］ 蒯松岩，汤锐智，马金洋，等.基于电感模型的开关磁阻电机参数优化［J］.电工技术学报，2015，7(7):97 -104.

［10］Dos Santos F L M，Anthonis J，Naclerio F，et al. Multiphysics NVH modeling:simulation of a switched reluctance motor for an electric vehicle［J］. IEEE Transactions on Industrial Electronics，2014，61(1):469 -476.

［11］Liu Z，Gao D. An AC drive test-platform of asynchronous motor［J］. Shanghai Haishi Daxue Xuebao，2010，31 (2):40 -44.