混杂系统故障诊断的粒子滤波与键合图方法

林吉凯 帕孜来·马合木提

(新疆大学电气工程学院，新疆 乌鲁木齐 830047)

0 引言

混杂系统是一类其所含元件同时包含了连续和离散状态行为的系统，对其进行准确的状态估计是设计其闭环控制系统和基于模型的故障诊断算法的关键。混杂系统的建模和诊断方法有多种［1-3］，其中，键合图对混杂系统建模有其独特的优势，在机械及电气系统中得到了广泛的应用;粒子滤波算法在递推非线性状态估计领域显示了其优越性，广泛应用于信号处理、经济学和工程学等领域，故障诊断是其中一个重要方面。文献［4］以混杂键合图为基础，提出基于功率的模式跟踪方法，可有效识别系统故障，但对计算要求高。文献［5］用粒子滤波实现了系统状态和参数的在线估计，但系统模型的精确性有待提高。

1 基于故障诊断的粒子滤波算法

1.1 粒子滤波理论

令非线性随机系统的状态空间模型为:

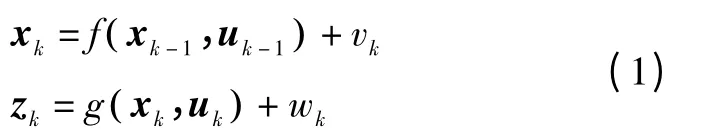
式中:xk∈Rn表示k 时刻的系统状态向量，其初始概率密度函数已知为p(x0);uk∈Rp表示k 时刻的输入(控制)向量;zk∈Rq表示输出向量;vk和wk分别为状态噪声和观测噪声;f(·)和g(·)分别表示状态转移函数和观测函数。

假设vk，wk，xk相互独立且vk和wk的分布已知，将系统状态看作是马尔科夫链的，即p(xk∣x0:k-1，z1:k-1，u1:k)=p(xk∣xk-1，uk)，粒子滤波就是通过系统的测量输出zk来递推构建状态的后验概率密度函数p(xk∣z1:k)。因此，粒子滤波包含两个阶段:预测和更新。预测阶段利用式(1)中的状态转移函数来预测前一时刻状态的概率密度，即先验概率密度。更新阶段利用最新的观测值，通过贝叶斯递推来修正先验概率密度，得到后验概率密度。这一过程可由以下三式说明:

其中，式(2)为k 时刻状态xk的先验概率密度，式(3)为后验概率密度。

这样，就可用离散加权来逼近时刻k 的后验概率密度函数:

这里δ(·)是狄利克雷函数，wk(i)是第i 个粒子的权值(i=1，…，N)。权值都是非负的，且所有粒子权值和为1，即:具体权值计算方法可参见重要性采样算法［6］。

粒子滤波的一个主要缺陷是粒子退化，即经多次迭代后，除一个粒子权值较大外，其他所有粒子权值均趋于零。这会导致大量时间浪费在传播对后验概率分布几乎无影响的粒子上。因此，必需对粒子进行重采样。粒子滤波达到理想近似效果所需要的最小粒子数可由有效采样值来计算:

因此，通过比较Neff和设定的阈值Nthr∈［1，N］就可判别是否出现了粒子退化。当Neff＜Nthr时，需要进行重采样。很多学者都提出了不同的重采样算法，具体可参见文献［7］～文献［9］。

1.2 混杂系统故障诊断的粒子滤波算法

混杂系统用一个离散模式集合表示系统的运行模型或故障状态，用一个连续变量集合模拟反应系统行为的连续变化值。一般来说，系统状态指模式加连续变量，模式仅是状态的离散部分。粒子滤波利用系统模型跟踪连续状态，并把估计状态作为观测函数来更新粒子权值。当粒子进入故障模式时，表明系统发生了故障，此时观测函数将会增加这些粒子的权值。

令S 为系统离散故障和运行模式的有限集，sk∈S为k 时刻检测到的系统模式，xk表示系统在k 时刻的多变量连续状态，{zk}为基于测量模型p(zk∣xk，sk)得到的系统状态观测序列。系统的任何故障和运行模式的变化都会改变其动态性能，粒子滤波对混杂系统进行状态估计和故障诊断就是利用后验概率密度p(xk，sk∣z1:k)来估计其边缘分布p(sk∣z1:k)。在混杂系统中，用{()，…，，)}表示系统状态的N 个采样或粒子，则式(6)可改写为:

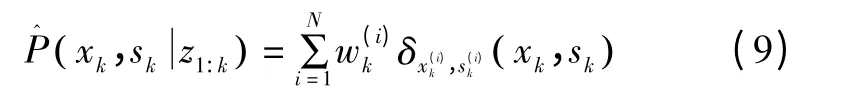
当N→∞时，式(9)会逼近真实的后验概率密度。

根据上述粒子滤波理论，给出混杂系统故障诊断的粒子滤波算法，图1 为算法的直观形式［10］。

图1 粒子滤波故障诊断算法Fig.1 Particle filtering fault diagnosis algorithm

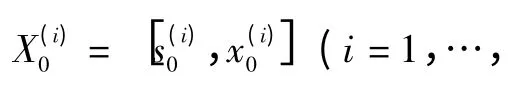
②预测。当从模式sk-1到模式(j=1，…，M，M为系统模式数目)的转移概率函数Tsk-1s(j)k不为零时，则在模式下，粒子。对每一模式计算重要性权值:

对模式sk中的所有粒子权值进行归一化处理。

④重采样。在模式sk下，根据权值大小，重采样N个新的粒子，取代原来的粒子。令k=k+1 并转步骤②。

2 三容水箱诊断键合图模型

2.1 三容水箱结构及故障分析

图2 给出了三容水箱的物理结构模型。该系统由三个串联水箱、储水槽、手动阀、电磁阀、水泵及控制器组成。每个水箱底部都装有压力传感器(P1、P2、P3)来测量水箱液位，传感器将测得的液位信号送入CPU，通过控制电磁阀的开闭达到控制水箱液位的目的。

图2 三容水箱系统结构Fig.2 Structure of the three-tank system

多容水箱系统故障主要分为三类:元部件故障、传感器故障和执行器故障。对如图2 所示的三容水箱系统来说，可能存在的故障有管道阻塞、水箱渗漏、电磁阀故障、控制器故障及压力传感器故障。据统计，在实际系统故障中，70% ～80%都是传感器故障。考虑到简化模型的需要，并结合实际工业现场故障发生概率情况，本文仅考虑三个传感器的故障。对其他故障，本文所提方法同样适用，仅故障越多，系统模型就越复杂，粒子滤波需要跟踪的系统模式也就越多。

2.2 水箱系统的键合图模型

键合图是一种图形化的系统动力学建模方法，在系统的键合图模型基础上，可对系统故障进行定性和定量的分析［11］。根据键合图理论，建立图2 所示三容水箱的键合图模型，如图3 所示［12］。

图3 三容水箱键合图模型Fig.3 Bond graph model of three-tank system

根据模型近似原理，在键合图模型中加入虚拟传感器，经转化得系统的诊断键合图，如图4 所示。

图4 三容水箱诊断键合图模型Fig.4 Diagnostic bond graph model of three-tank system

图4 中，Mse 为外部顶点势源，其值为势传感器的测量输出me;Df1、Df2、Df3分别相当于实际系统中的三个压力传感器P1、P2、P3的测量值，传感器的输出为水箱液面高度:mei= hi(k)，i=1，2，3。根据图4 所示的水箱诊断键合图模型，可得系统的结构方程，如表1所示。

表1 诊断键合图的结构方程Tab.1 Structural equations of diagnostic bond graph

对节点01组成的结构方程，由键合图元的静态函数关系可得:

式中:Df1为传感器的测量值。这表明，影响传感器P1输出的参数为Sf、C1、me1、R1和R2。根据节点02和03的结构方程，可分别推出式(11)、(12)如下:

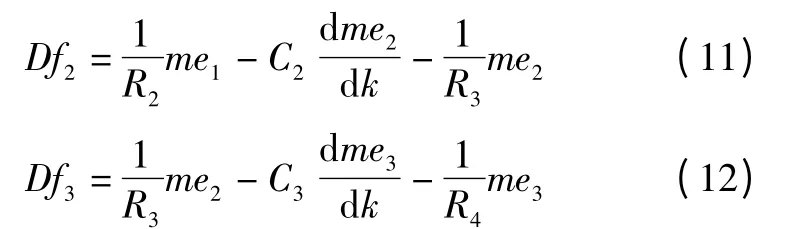
这表明，影响传感器P2输出的参数为R2、me1、me2、C2和R3，影响传感器P3输出的参数为R3、me2、me3、C3和R4。以上各式中，Ri表示管道的阻力，Ci表示水箱的水容量，Sf 表示水泵的流速，fi、ei(对应表1 中的f、e)分别为键合图的流和势变量。

3 传感器故障仿真分析

3.1 故障模式

用粒子滤波方法跟踪系统运行模式需借助系统的状态方程，把式(10)、(11)、(12)改写为:

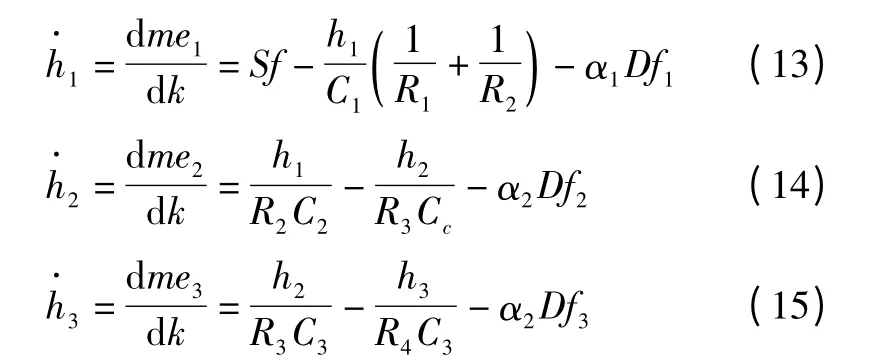
以上三式中，αi∈ 0，[ ]1 为传感器故障系数，αi=1表示传感器无故障，αi=0 表示传感器完全损坏。

本系统有三个传感器，因此故障模式有23=8 种。表2 给出了系统所有模式(正常模式和故障模式)及判别标准。

表2 故障模式Tab.2 Fault modes

令系统的连续状态向量为x =［h1，h2，h3］T，则系统的状态方程可描述为［13］:

其中，q∈{m0，m1，m2，m3，m4，m5，m6，m7}表示系统的离散模式，u(k)表示电磁阀控制信号，v(k)表示状态噪声。

3.2 故障仿真分析

假设初始时三水箱液位相同:h1= h2= h3=45 cm，且α1=α2= α3=1。系统运行时，阀门全部打开。当系统运行到k =100 s 时，设置α2=0.75，系统进入模式1;当系统运行到k=200 s 时，设置α1=0.5，α3=0.6，系统进入模式5。图5 给出了粒子滤波状态估计结果，图6 是水箱1 的液位变化。

图5 系统状态估计结果Fig.5 Result of system state estimation

图6 水箱1 的液位变化Fig.6 Liquid level change of tank-1

从图5 可以看出，系统约10 s 后进入稳定状态;在100 s 时，状态发生波动，但由于此时设定的阈值α2=0.75 接近正常状态(0.8)，粒子滤波器在跟踪约30 s后恢复正常状态;在200 s 时，由于传感器发生了显著故障，粒子滤波器很好地捕捉到了系统状态变化。系统正常运行时，水箱液位应保持恒定，由图6 可以看出，水箱1 的液位在100 s 和200 s 时发生变化，表明传感器P1发生了故障。

4 结束语

混杂系统由于复杂的性质，在建模和故障诊断上存在很多挑战。本文介绍了一种粒子滤波和键合图相结合的混杂系统故障诊断方法，针对三容水箱传感器故障，经理论分析和仿真实验验证了该方法的有效性。该方法结合了两种理论的各自优势，对实现混杂系统的故障诊断有一定的借鉴意义。下一步的工作是将该方法应用到THJ-2 型高级过程控制系统实验装置中，实现其在实际系统中的应用。

［1］ 李卫东，刘曰锋.混杂系统研究综述［J］. 自动化技术与应用，2008，27(1):1 -4.

［2］ 王文辉，刘帅，周东华.混杂系统故障诊断方法综述［J］.系统工程与电子技术，2006，28(12):1853 -1857.

［3］ 郑刚，谭民，宋永华. 混杂系统的研究进展［J］. 控制与决策，2004，19(1):7 -11.

［4］ Arogeti S A，Wang D，Low C B，et al.Energy-based mode tracking of hybrid systems for FDI［J］. Systems Man and Cybernetics:Systems，IEEE Transactions on，2013，43(1):14 -28.

［5］ 莫以为，萧德云. 基于进化粒子滤波器的混合系统故障诊断［J］.控制与决策，2004，19(6):611 -615.

［6］ Doucet A，Godsill S，Andrieu C. On sequential monte carlo sampling methods for bayesian filtering ［J］. Statistics and Computing，2000，10(3):197 -208.

［7］ Candy J V. Bootstrap particle filtering［J］. Signal Processing Magazine，IEEE，2007，24(4):73 -85.

［8］ Liu J S，Chen R，Logvinenko T. A theoretical framework for sequential importance sampling with resampling［C］//Sequential Monte Carlo Methods in Practice.Springer New York，2001:225 -246.

［9］ 杜京义，殷梦鑫. 一种改进的粒子滤波算法应用于故障诊断［J］.系统仿真学报，2014，26(1):62 -66.

［10］Tafazoli S，Sun X.Hybrid system state tracking and fault detection using particle filters［J］. Control Systems Technology，IEEE Transactions on，2006，14(6):1078 -1087.

［11］王中双.键合图理论及其在系统动力学中的应用［M］.哈尔滨:哈尔滨工程大学出版社，2000.

［12］帕孜来·马合木提，董小亮，杨莲，等. 新型解析冗余关系法在传感器故障诊断中的应用［J］. 传感器与微系统，2014，33(7):157 -160.

［13］Koutsoukos X D.Estimation of hybrid systems using discrete sensors［C］//Decision and Control，2003. Proceedings. 42nd IEEE Conference on.IEEE，2003:155 -160.