Walsh 变换与数学形态学的特征提取对比研究

经 哲 郭 利

(军械工程学院导弹工程系，河北 石家庄 050003)

0 引言

液压泵是液压系统的“心脏”，其性能好坏直接决定着整个液压系统能否正常运行。液压泵的振动信号因包含丰富的状态信息，且易于获取，是分析液压泵故障诊断重要的特征信号之一。对于轴向柱塞式液压泵而言，其振动信号常含有较多的冲击成分，因此，对液压泵振动信号中冲击成分的频率特征进行提取，是实现液压泵故障诊断的基础。

Walsh 变换与数学形态学近年来常被用于信号的特征提取［1-6］。Walsh 变换与Fourier 变换相似，也是信号的处理方法之一，与建立在复数乘法之上的Fourier 变换相比，Walsh 变换中只有简单的加减法，所以Walsh 变换的计算速度极快，其相应的功率谱较Fourier 功率谱而言，敏感性和抗噪能力更强［6］。数学形态学［7］通过结构元素探针在信号中的移动可以提取信号的冲击特征，和时域、频域的其他数学方法不同，其抑制脉冲干扰能力较强［8］。

针对液压泵振动信号常含有冲击成分的问题，本文将Walsh 变换和数学形态学引入到信号特征提取中来，通过仿真和实验分析，数学形态学在提取信号冲击特征频率方面优于Walsh 变换。

1 Walsh 变换

Walsh 函数系是一组完备的正交函数系，由+1 和-1 两个元素构成。在实际工程应用中，常利用离散Walsh 变换处理有限长序列离散信号。离散Hadamard变换和离散Walsh 变换本质上相同，只是排列次序略有差异。Hadamard 变换具有简单的递推关系，对于高阶矩阵的计算其更加简单直接，因此，常利用Hadamard 变换进行高阶矩阵的计算。

离散Hadamard 变换的代数式可定义为:

式中:{B(K)}为Hadamard 变换后的系数序列;K =0，1，2，…，N-1;n=0，1，2，…，N-1。

根据矩阵形式的定义，可得Hadamard 变换的矩阵定义式:

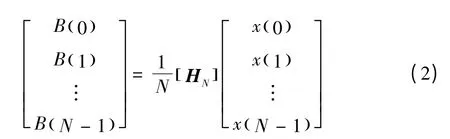
式中:HN为N 阶Hadamard 矩阵。

常见的Walsh 变换有三种排序方式，分别为Walsh序、Paley 序和Hadamard 序。三种序列之间可以互相转换，关系如下:

在计算功率谱时，常选用Walsh 序的变换系数:C(0)，C(1)，…，C(N-1)，则Walsh 变换的功率谱为［9］:

2 数学形态学

2.1 数学形态学基本运算

数学形态学的基本运算包含腐蚀和膨胀两种算子［10］。设一维多值信号x(n)的定义域为X = {0，1，2，…，N-1}，一维结构元素序列y(n)的定义域为Y={0，1，2，…，M-1}，其中N 和M 都是整数，且N ＞M，则x(n)关于y(n)的膨胀和腐蚀分别定义为:

数学形态学中的腐蚀运算有抑制正向冲击和平滑负向冲击的作用，而膨胀运算则相反，在平滑正向冲击的同时抑制了负向冲击。

利用腐蚀和膨胀的概念，可将x(n)关于y(n)的开、闭运算分别定义为:

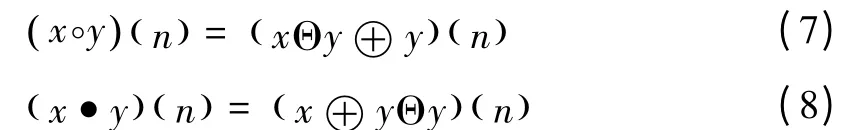
数学形态学中的开运算常用来去除信号边缘的毛刺，同时可以滤除信号上方的峰值噪声;闭运算常用于平滑或抑制信号下方的波谷噪声，起到填补信号漏洞和裂纹的作用。

2.2 形态学滤波器

利用形态学的开、闭运算可以构建两种常用的滤波器:平均滤波器(AVG)和差值滤波器(DIF)。二者分别表示如下:

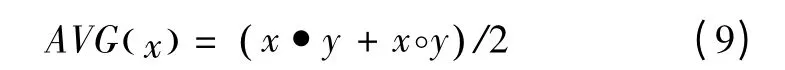
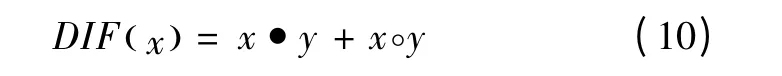
AVG 可以在消除信号正、负冲击的同时平滑信号，而DIF 可以提取信号中的正、负冲击。

2.3 形态学结构元素

结构元素形状和大小的选择对滤波效果有重要的影响，是形态学的基本算子之一。常用的形状有三角、半圆、菱形等。结构元素越复杂，计算量越大，提取信号的效果也越好。考虑到提取效果和计算量等综合因素，处理信号时常选用扁平的圆盘形作为结构元素［11］。

3 仿真信号分析

在对比研究中，采用如下形式的仿真信号模拟液压泵出现故障时的振动信号:

在信号s(t)中，冲击分量包含两部分［12］:x1(t)模拟液压泵振动信号中的固有冲击成分，x2(t)模拟液压泵出现故障时故障引起的冲击成分。n(t)代表白噪声成分，加噪后信号的信噪比为-5 dB。仿真信号的采样频率为2 048 Hz，采样点数4 096。图1 为s(t)的时域图和频谱图。

图1 仿真信号的时频图Fig.1 The time-frequency diagram of simulation signal

由仿真信号易得，信号冲击成分的能量主要集中在270 Hz。现分别利用Fourier 功率谱、Walsh 功率谱和形态学差值滤波器对信号进行特征提取，结果如图2 所示。由仿真图可以看出，Fourier 功率谱在提取10 Hz和30 Hz 的冲击频率特征的同时，能够提取10 Hz的2 倍频，但是15 Hz 和26 Hz 混淆了频率特征的提取。Walsh 功率谱提取的9.75 Hz 与29.75 Hz 与冲击成分频率十分接近，但是其提取出46.75 Hz 与87 Hz 亦对频率特征的提取造成一定的影响。由形态学差值滤波器对频率特征进行提取，能准确地提取10 Hz的1、2、3、4 倍频和30 Hz 的1、2 倍频，10 Hz 的3 倍频和30 Hz 相重合，所以30 Hz 处的频谱幅值较大。综上所述，形态学差值滤波器的特征提取效果最好。

图2 特征提取曲线Fig.2 Feature extraction curves

4 液压泵实测信号分析

在液压泵的常见故障模式中，斜盘磨损和滑靴松动是最容易发生的两种故障。滑靴与斜盘之间的摩擦副是斜盘式轴向柱塞泵多对摩擦副中最复杂的一对［13］，对液压泵的性能影响较大。在液压泵工作过程中，出现斜盘磨损故障或出现松靴故障时，都会影响其正常工作，降低液压泵寿命，甚至发生重大事故。

本文采用的试验器件名称及型号如表1 所示。

表1 试验器件名称及型号Tab.1 The name and model number of experimental devices

其中，驱动电机的额定转速为1 480 r/min;液压泵的柱塞数为7，理论排量为10 ml/r，额定转速为1 500 r/min，液压泵主溢流阀压力为10 MPa，采样频率为20 kHz，采样点数为10 000。由于泵轴的转速为1 500 r/min，单个柱塞附加冲击的基频为f = n/60(n 为电机的转速)，则本试验的液压泵的冲击振动基频为1 480/60 ×7 =172.667 Hz。

采集到的松靴和斜盘磨损的信号的时频图分别如图3、图4 所示。

图3 松靴状态下的时频图Fig.3 The time-frequency diagram of loose slipper state

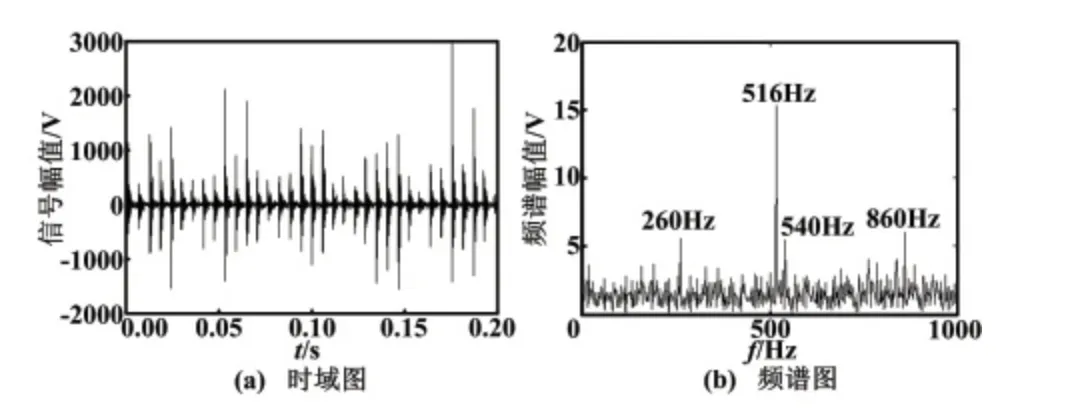
图4 斜盘磨损状态下的时频图Fig.4 The time-frequency diagram of swash-plate wear state

从采集信号的频谱图中只能看出液压泵振动信号的能量主要集中在几个频率上，并不能提取信号基频等频率特征。下面分别对振动信号求取Fourier 功率谱、Walsh 功率谱以及通过形态学差值滤波器提取信号的特征频率，结果如图5 所示。

图5 斜盘磨损信号特征提取曲线Fig.5 Featur e extraction curves of swash-plate wear te signal

图5 中，A 代表振幅。由图5 对比分析可得，Fourier 功率谱提取出的170.9 Hz、354 Hz 和517.6 Hz与理论分析的基频172.667 Hz、2 倍频345.334 Hz 和3 倍频518.001 Hz 较为接近，但频谱幅值较低，效果一般。Walsh 功率谱提取出的接近基频的170.9 Hz 幅值较高，频率特征较明显，但358.9 Hz 与859.4 Hz 与2 倍频345.334 Hz、5 倍频863.335 Hz 相差较多，且提取出的频率有干扰成分。由形态学差值滤波器提取的172 Hz、344 Hz、516 Hz 与688 Hz 与理论分析的基频及其2、3、4 倍频较为接近，效果最好。松靴信号特征提取曲线如图6 所示。

图6 松靴信号特征提取曲线Fig.6 Feature extraction curves of loose slipper state signal

由图6 对比分析可得，Fourier 功率谱提取的344.2 Hz与振动信号基频的2 倍频较为接近;而Walsh功率谱提取的168.5 Hz 与178.2 Hz 在基频附近，但是基频已被湮没，48.83 Hz 等频率对特征频率的分析噪声一定的影响。形态学差值滤波器提取的172 Hz、344 Hz与振动信号的基频及其2 倍频较为接近，虽然50 Hz 等频率也有一定的影响，但基频幅值较高，可以提取信号的特征频率。

5 结束语

传统的Fourier 功率谱与Walsh 功率谱、形态学差值滤波器均能提取液压泵振动信号的特征频率，为故障预测和诊断打下良好基础。通过仿真试验和液压泵模拟故障实验，结果表明，形态学差值滤波器在提取频率特征方面优于Fourier 功率谱和Walsh 功率谱。

［1］ 杨宇祥，吕林涛，乐静，等. 基于Walsh 函数的多频率同步信号合成方法［J］.仪器仪表学报，2011，32(7):1540 -1545.

［2］ 郝博，王军，王昭诚.基于Walsh 序列的云传输广播网的扩频编码［J］.清华大学学报:自然科学版，2014，54(4):413 -418.

［3］ 贾宏雷，江桦，王权. 基于形态学处理的突发信号宽带检测算法［J］.太赫兹科学与电子信息学报，2013，11(6):911 -916.

［4］ 王凤利，段树林，于洪亮，等.基于EEMD 和形态学分形维数的柴油机故障诊断［J］.内燃机学报，2012，30(6):557 -562.

［5］ 卢绪祥，刘雨佳，李录平，等.形态滤波在滑动轴承声发射信号降噪中的应用［J］.动力工程学报，2013，33(4):278 -284.

［6］ 肖杰，刘树林，上官长存，等.Walsh 变换在滚动轴承早期故障特征提取中的应用［J］.轴承，2010(2):44 -47.

［7］ SERRA J.Morphological filtering:an overview［J］.Signal Process，1994，38(4):3 -11.

［8］ 侯高雁，吕勇，肖涵，等.基于EEMD 自适应形态学在齿轮故障诊断中的应用［J］.振动与冲击，2014，33(18):145 -148.

［9］ 李宝安，李行善，刘星.Walsh 变换对冲击信号序列特征提取的研究［J］.北京航空航天大学学报，2003，29(9):802 -806.

［10］罗洁思，于德介，彭富强，等.基于EMD 的多尺度形态学解调方法及其在机械故障诊断中的应用［J］.振动与冲击，2009，28(11):84-86.

［11］赵昭，刘利林，张承学，等.形态学滤波器结构元素选取原则研究与分析［J］.电力系统保护与控制，2009，37(14):21 -25.

［12］Wang Yukui，Li Hongru，Ye Peng. Fault feature extraction of hydraulic pump based on CNC de-noising and HHT［J］.Journal of Failure Analysis and Prevention，2015，15(1):139 -151.

［13］张长英，龚晓群，李萍萍，等. 斜盘式轴向柱塞泵的减摩降噪措施［J］.液压与气动，2013(12):118 -120.