周期热作用下房间辐射传递函数实验研究

李 丽，王丽慧，黄 晨，吕留根，陈剑昌，白天宇

(上海理工大学 环境与建筑学院，上海 200093)

房间得热与负荷不等的原因是得热中存在辐射得热，在不考虑潜热负荷时，房间瞬时动态负荷也可等于瞬时对流得热与辐射负荷之和，为此空调房间辐射负荷是形成空调动态负荷的关键因素。目前广泛应用的动态负荷计算方法包括谐波反应法、反应系数法和传递函数法［1－2］。其中，在应用传递函数法计算房间负荷时，采用传递函数系数和房间得热便可计算获得房间负荷［3］。房间传递函数表征房间总负荷和房间总得热的关系，而辐射传递函数则表征房间辐射负荷和房间辐射得热的关系。目前，各学者对房间传递函数以及常用方法计算空调负荷的研究较多，Chen 和Yu［4］在对香港气象参数的研究中得到了3 ～5 个z 传递函数系数以反映建筑围护结构特性。上海交通大学连之伟教授［5］通过建立模型实验，求解得到了房间传递函数系数及其变化规律，该校谷波教授对比研究了Z 传递函数法和辐射时间序列法计算空调负荷［6］的不同，并编辑软件［7］简化了空调动态负荷计算。在大空间非空调区向空调区转移的辐射得热中，如何计算由此形成的辐射负荷是大空间分层空调负荷计算的关键问题之一，但目前对于辐射传递函数系数的研究较少，关于壁面辐射特性以及辐射负荷的研究更少。本文试图通过实验的方法求解房间辐射传递函数系数，同时通过实验研究房间辐射负荷与各面辐射负荷的变化特性，为大空间辐射转移负荷的研究提供实验依据。

1 房间辐射传递函数实验原理

仅对绝热房间某一壁面加热，以此作为房间唯一热源。高温加热面通过辐射热传递将引起各非加热面壁温升高，各面接受辐射得热后，部分辐射得热被房间围护结构吸收和贮存，另一部分则与空气进行对流换热，形成房间辐射负荷。即在绝热房间内，定义各非加热面的净辐射得热量之和为房间辐射得热QR，而各非加热面接受高温加热面辐射得热后产生的对流得热则为该面的辐射负荷，定义房间辐射负荷Qi，d为各非加热面的对流得热量(辐射负荷)之和，该房间辐射负荷可通过实验结果计算得到。房间辐射传递函数则可由辐射负荷根据最小二乘法［8］拟合获得。

1．1 房间辐射得热

考虑到房间各面进行辐射热传递为多次反射和吸收，故采用有效辐射法计算房间辐射换热量。对于一个封闭的空间，某表面的有效辐射为本身辐射和其它表面投射辐射的反射之和，即房间各面有效辐射换热量Ji(i=1，2…6)可采用下式［9］计算

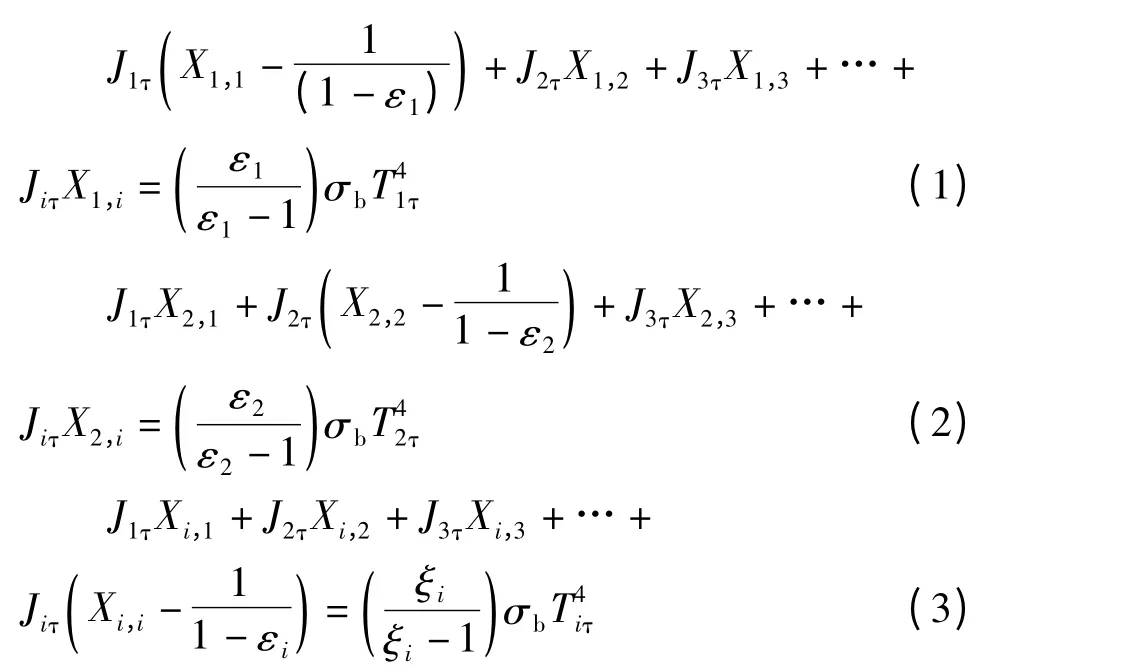
式中

σb——黑体辐射常数/W·m－2·℃－4，σb=5.67 ×10－8W/(m2·℃4);

Tiτ——τ 时刻壁面i 的温度/℃;

Jiτ——τ 时刻壁面i 的有效辐射/W·m－2;εi——壁面i 的发射率;

Xi，i——壁面i 对于壁面i 的角系数。

根据式(1)～式(3)可计算房间各面的净辐射得热量，其计算如式(4)

式中 qriτ——τ 时刻壁面i 的净辐射得热量/W，

(i=1，2……5);

Ebiτ——τ 时 刻 黑 体 辐 射/W·m－2，Ebiτ=σbT4iτ。

房间辐射得热为各非加热面的净辐射得热量之和，计算式如式(5)

式中 Qrτ——τ 时刻房间辐射得热/W;

Ai—— 壁面i 面积/m2。

1．2 房间辐射负荷

绝热房间各非加热面在获得辐射热以后，会部分形成负荷，采用热平衡方法，便可对各壁面进行对流辐射分离［10］，即

式中 CLQriτ——τ 时刻壁面i 的辐射负荷，即壁面

接受辐射热后形成的对流热/W;

qiτ——τ 时刻壁面i 热流/W·m－2(采用建通热流密度计和里氏热流计测得)。

通过实验测得qiτ，便可通过式(4)和式(6)计算获得各非加热面的辐射负荷，由各非加热面对流换热量之和即为房间辐射负荷CLQrτ1，计算式如式(7)

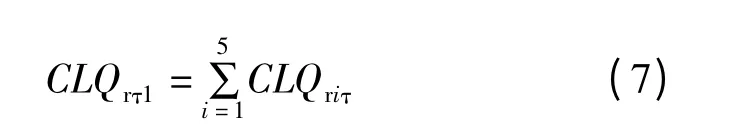
另一方面，基于绝热房间假说，由房间热平衡计算得到房间辐射负荷如式(8)

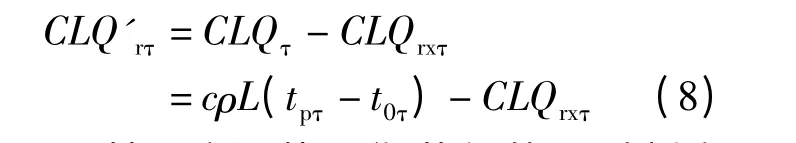
式中 CLQ'rτ——基于房间热平衡获得的τ 时刻房间辐射负荷/W;

CLQτ——τ 时刻房间总负荷/W，(由该时刻的房间送、回风实验值计算获得);

CLQrxτ——τ 时刻房间x 加热面分离的对流热负荷/W，(也可由x 面热平衡计算);

c——空气比热/J·kg－1·℃－1，取c =1005J/kg·℃;

L——房间送风量/m3·s－1;

t0τ、tpτ——τ 时刻送、回风温度/℃;

ρ——空气密度/kg·m－3。

利用各面辐射分离求解获得辐射负荷式(7)与采用实验热平衡获得辐射负荷的相对误差定义式(9)，以判别论文实验的准确性，各工况相对误差采用了周期内各实验值平均值，从而获得各工况δ1为

1．3 房间辐射传递函数

由式(5)和式(7)获得房间辐射得热和辐射负荷后，采用最小二乘法便可计算房间辐射传递函数系数，其辐射负荷计算式［11］如式(10)

其中，v0为当前计算时刻的辐射得热转变成当前辐射负荷的比例，v1是前一时刻的辐射得热转变为当前时刻辐射负荷的比例;而ω1通常为负值，说明在计算即时辐射负荷时，必须计入前一时刻的部分辐射负荷。同理，其相对误差定义为，各工况相对误差δ2与δ1相同的处理方法。

2 实验设计

2．1 实验系统

实验小室(2．5 m×2．1 m×2．5 m)位于建筑中间层区，小室四面墙体和顶板为100 mm 厚聚氨酯保温库板制作，地面为2 mm 厚不锈钢板，房间各面均贴有2 mm 厚的电热膜。该实验房间位于一普通空调房间之中，没有外墙。环境室内温度可控，实验小室内景构造如图1，风口布置见图2。

图1 实验室内景图

图2 实验室风口

图3 实验系统原理图1 －表冷器;2 －电加热;3 －变频送风机;4 －空气处理机组;5 －送风口;6 －回风口;7 －电热膜加热面(南墙);8 －电热膜调压器

如图3 所示为实验系统原理图，室内气流组织为顶部散流器送风，风道沿屋顶敷设。整个空调系统采用全新风送风，回风直接排出室外。实验中房间回风温度主要由表冷器1 和电加热2 调节控制;房间送风量则采用变频送风机3 调节控制;南墙壁面电热膜7 由电热膜输入功率的调压器8 调节，实验时以模拟输出功率的周期性变化为调节目标。

2．2 实验方法与实验工况

考虑到加热面内加热电热丝布置并非完全均匀，正式实验前，首先进行了各壁面的温度和热流密度的均匀性代表测点预实验，根据均匀性实验结果设计了如图4 的测点布置方案。实验中共布有温度测点23 个，热流密度测点10 个。其中南墙加热面，贴有4 个温度测点，2 个热流密度测点，其它墙面贴有2 个温度测点，东、西、北墙面各贴有2、3、1 个热流密度测点;屋顶、地面各贴2 个温度测点和1 个热流密度测点。送、回风风口各有温度测点3 个;室内仅布1 根测线共3 个测点以测量垂直方向空气温度。另采用风量罩测定实验风量。实验中各参数测量用仪器性能见表1。

图4 实验温度和热流测点布置图

表1 实验仪器的性能参数

实验中南墙电热膜输入功率为周期性变化，以获得周期性扰量作用下的房间辐射负荷。实验时室内空气温度设定为25℃。实验在变壁面平均热流和变换气次数(改变房间通风量)两种变参数条件下进行，共5 个实验工况，且实验中每个工况均进行多个连续周期的实验，以消除壁温等实验参数初始条件的影响。实验结果表明，对研究对象进行2 个及以上的周期后，前后两个周期对应时刻的加热面和非加热面壁温最大误差分别为2．1%和7．0%，此时可认为最后周期的壁温基本无初始条件的影响。下述研究分析均以最后一个周期的实验结果为依据，实验各工况详见表2。

表2 实验工况表

3 实验结果及分析

3．1 热平衡及其辐射传递系数实验结果及分析

根据式(1)～式(8)，在热平衡实验中，获得变壁面热流和变换气次数两种实验条件下实验分离辐射负荷δ1平均误差为7．4%，最大11．5%，说明该文提出的辐射分离方法计算辐射负荷合理、可行，详见表3。

采用最小二乘法并利用分离所得辐射负荷，可获得各工况下平均辐射传递函数系数，由此计算房间辐射负荷CLQr2，详见表3，结果表明，传递函数法计算的辐射负荷相对误差δ2各工况均小于15%，平均误差10．5%，基本满足ASHRER 数据传递函数的小于20%的分类标准［12］，即可归为一类传递函数。

图5 展示工况2 扰量、分离辐射负荷以及传递函数计算辐射负荷曲线，两曲线与图中热平衡实验获得辐射负荷均极为吻合，所以可认为用实验分析方法求解辐射传递函数进而计算辐射负荷可行。

表3 实验条件下房间辐射传递函数系数和辐射负荷

房间辐射传递函数系数主要和围护结构材料有关［11］。本实验中，两种变参数即加热面加热量和室内换气次数变化条件下，其辐射传递系数变化均较小，采用辐射传递函数均值各工况中引起的最大误差分别为:6．5%、7．3%、8．2%、8．0%、5．7%，均在10%以内。因此可以认为变壁面加热量和换气次数对辐射传递函数影响可以忽略。

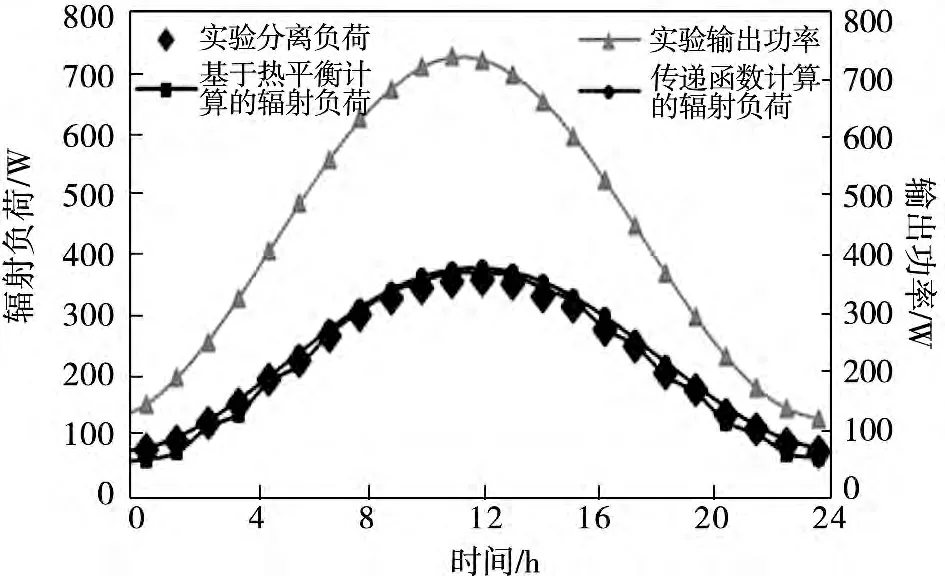
图5 Case2 房间分离辐射负荷和基于热平衡计算的辐射负荷对比分析图

3．2 辐射负荷特性分析

按式(6)可得工况2 和工况5 房间各壁面辐射负荷，见图6 ～图7。由图可知，房间各壁面辐射负荷变化规律相似。其中，房间各面中北墙的辐射负荷最大，屋顶的辐射负荷最小，且各面辐射负荷达到峰值的时间几乎相同。这是因为房间南墙为加热面，北墙与南墙角系数最大，即从南墙获得的辐射能量最多，即在其它实验条件不变的情况下，角系数越大的表面，辐射负荷越大;对于房间的屋顶和地面，与南墙具有相同的角系数，但屋顶布有送、回风口，有效面积较小，此外因室内略有分层现象，屋顶壁面温度甚至要高于地板温度2℃左右，屋顶辐射换热也比地板要低，从而导致屋顶辐射负荷较小。

图6 Case2 房间各面辐射负荷

图7 Case5 房间各面辐射负荷

图8 变壁面热流条件下北墙辐射负荷

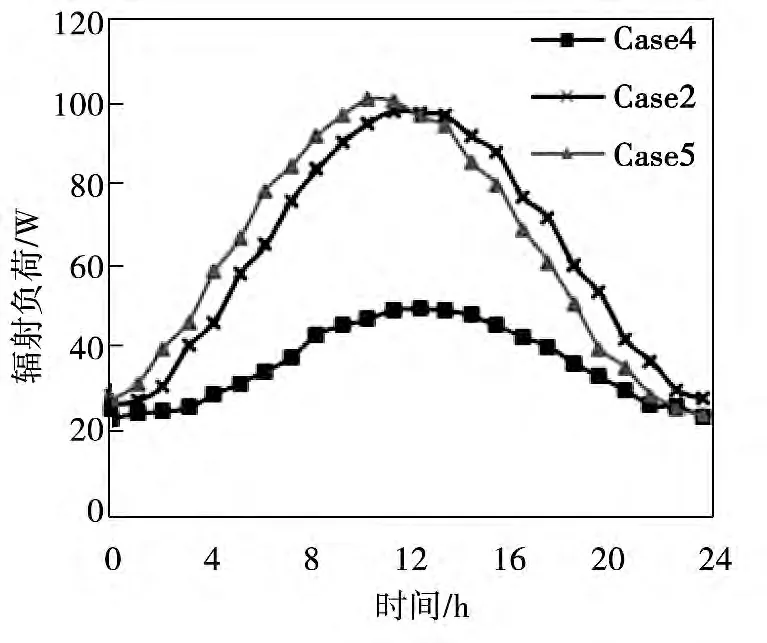
图9 变换气次数条件下北墙辐射负荷

图10 两种变参数条件下北墙辐射负荷均值变化曲线

研究变壁面热流和变换气次数条件下北墙的辐射负荷特性，由图8 可得，随着房间壁面热源增大，北墙辐射负荷峰值增大，辐射负荷达到峰值的时间略短，这是由于实验房间蓄热能力有限，扰量增加时，随着壁面热流的增加，房间辐射得热转化负荷量较大;由图9 可得，在变换气次数条件下，北墙辐射负荷变化曲线略有不同。随着换气次数增大，北墙辐射负荷均减小，且辐射负荷达到峰值的时间逐渐减小，这是因为对流换热系数受换气次数影响所致，随着换气次数增大，对流换热系数会有所增加［13］，对流换热增强，则相应辐射换热减小，辐射负荷峰值也会有所降低。图10 为北墙辐射负荷均值随变壁面热流均值和房间换气次数增加的变化曲线。壁面热流均值增加，辐射负荷均值随之增加，但并非线性增加，而房间换气次数增加，辐射负荷均值接近线性变化。

4 结论

(1)实验热平衡条件下，对比分析变壁面热流和变换气次数两种实验条件的分离辐射负荷，其相对平均误差为7． 4%，说明实验系统热平衡条件较好;

(2)通过实验可获得变壁面热流和变换气次数条件下的辐射传递函数系数，采用传递函数均值计算的辐射负荷相对热平衡条件下的辐射负荷的平均误差10．5%，共同反映实验系统和均值辐射传递函数系数两者因素的综合影响;

(3)对比分析实验各工况采用传递函数均值计算的辐射负荷与实验分离辐射负荷，其最大相对误差均在10%以内，说明通过实验方法获得房间辐射传递函数的方法可行;

(4)讨论房间墙面辐射负荷特性结果表明，房间各壁面辐射负荷变化规律相似，与加热面对立的壁面辐射负荷最大，且该面辐射负荷均值随着壁面热源的增大非线性增加，随换气次数的增加近似可认为线性降低。

［1］Stephaenson D G，Mitalas G P． Cooling load calculations by thermal response factor method［J］． ASHRAE Transactions，1967，73(3):1．1 －1．7．

［2］Mitalas G P． Comments on the z －transfer function method for calculating heat transfer in buildings［J］．ASHRAE Transactions，1978(84):667 －674．

［3］罗智特，杜雁霞，贾代勇．空调动态负荷计算方法及比较［J］．制冷与空调，2005，5(2):57 －61．

［4］TY Chen，Z Yu． A statistical method for selection of sequences of coincident weather parameters for design cooling load calculations［J］．Energy Conversion and Management，2009(8):13 －821．

［5］连之伟，马仁民，李海林．下送风室内热源条件下房间传递函数的实验研究［J］．西安冶金建筑学院学报，1992，24(2):123 －129．

［6］黄彬彬，谷波，韩华．房间空调逐时冷负荷两种计算方法的比较［J］．流体机械，2009，7(1):64 －66．

［7］王朋．建筑空调动态负荷计算分析［D］．上海:上海交通大学，2008．

［8］姚君磊，赵红，赵凯璇，等． 基于最小二乘法的NTC热敏电阻动态标定方案探究［J］． 节能技术，2013，31(4):363 －366．

［9］章熙民，任泽霈，梅飞鸣．传热学［M］．5 版．北京:中国建筑工业出版社，2007:237 －238．

［10］王丽，刘志铮，王岳人． 低温地板辐射采暖埋管结构尺寸设计实验研究［J］．节能技术，2010，28(1):11 －14．

［11］赵荣义，范存养，薛殿华，等．空气调节［M］．4 版．北京:中国建筑工业出版社，2009:48 －49．

［12］EF Sowell，Classification of 200640 parametric zones for cooling load calculations［J］．ASHRAE Transactions，1988b，94(2):754 －777．

［13］马仁民，顾瑞英，邢秀强． 集中热源送风房间墙体内侧对流放热系数实验研究［C］． 王如竹编． 全国暖通空调制冷1990 年学术年会资料集(上)． 北京:中国制冷学会，1990:182 －185．