改进重复控制在低采样频率逆变器中的应用

赵强松 叶永强 徐国峰 竺明哲 潘 雪

(1.南京航空航天大学自动化学院 南京 2100162.中原工学院电子信息学院 郑州 450007)



改进重复控制在低采样频率逆变器中的应用

赵强松1，2叶永强1徐国峰1竺明哲1潘 雪1

(1.南京航空航天大学自动化学院 南京 2100162.中原工学院电子信息学院 郑州 450007)

针对低采样频率逆变器传统控制方法控制效果不理想的问题，提出采用分数相位超前补偿重复控制(FPLCRC)策略；在分析传统重复控制存在问题的基础上，给出相位超前补偿提高控制系统稳定性的原理，根据逆变器稳定性和稳态误差的要求，分别设计补偿环节的陷波器、低通滤波器和分数超前拍次，并采用拉格朗日插值方法予以实现；最后通过MATLAB/Simulink进行建模和分析，所搭建的逆变器实验平台验证了方法的正确性和可行性。

低采样频率 逆变器 重复控制 分数相位超前补偿 拉格朗日插值

0 引言

恒压恒频(Constant Voltage Constant Frequency，CVCF)脉宽调制(Pulse-Width Modulation，PWM)变换器广泛用于各种工业场合。非线性负载及死区导致的谐波严重影响变换器输出波形质量。

重复控制(Repettive Control，RC)将重复信号发生器作为内模置于闭环系统中，可完全跟踪周期参考信号或抑制周期扰动信号，实现极低的稳态误差，目前已应用于不间断电源(UPS)[1，2]、动态电压调节器(DVR)[3]、有源滤波器(APF)[4]、逆变器[5-8]等场合。

随着变换器功率等级的提高，为了减少运行损耗，PWM开关频率随之降低，而一般变换器系统的采样频率等于或2倍于开关频率[9，10]，因此，系统的采样频率也会降低。而目前重复控制在变换器中的良好控制效果都是在高采样频率(10 kHz或以上)下取得的[1-8]。但高采样频率不仅需要高精度、高速率的传感器，而且由于控制器需要对采集的数据进行实时处理和分析，高采样频率还会过多的占用CPU的时间和内存资源。因此，如果适当降低采样频率也能够取得良好控制效果，将大大节约系统成本。但采样频率的降低将会严重影响变换器输出波形质量，甚至导致重复控制器不稳定。

相位超前补偿重复控制(Phase Lead Compensation Repetitive Control，PLCRC)可补偿相位滞后、增加控制带宽、提高系统跟踪精度和误差收敛速度[8，11，12]。但在低采样频率变换器中，传统整数超前相位补偿重复控制将不能满足系统稳定的需要。

本文以独立逆变器为例，针对其低采样频率时存在系统不稳定的问题，分析整数相位超前补偿重复控制在低采样频率情况下过补偿或欠补偿的缺陷，从而引入分数相位超前补偿环节。进而对分数相位超前重复控制器重新设计，并给出其设计步骤和依据。采用拉格朗日插值理论实现了分数超前拍次的相位补偿。最后通过Matlab/Simulink进行仿真和分析，并搭建了一台单相独立逆变器实验样机，验证了方法的正确性和可行性。

1 单相逆变器数学模型

单相独立逆变器数学模型如图1所示。

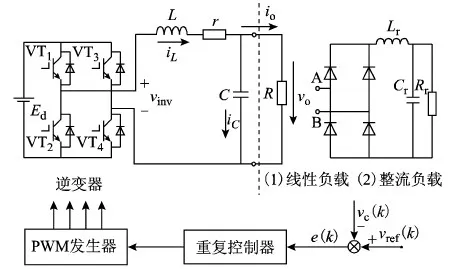
图1 重复控制逆变器系统

图1中L为滤波电感，C为滤波电容，r为考虑死区时间及电感电阻等因素的等效电阻，R为线性负载，Lr、Cr和Rr构成整流负载，io为输出电流，iL为电感电流，iC为电容电流，Ed为直流母线电压，vinv为逆变器输入电压。以电感电流和电容电压为状态变量，其连续状态空间方程为

(1)

逆变器输入电压vinv与输出电压vc之间的传递函数GP(s)为

(2)

2 低采样频率下传统PLCRC存在的问题

目前大多数逆变器重复控制策略都是在高采样频率下取得良好的控制效果，但在某些应用场合，采用较低采样频率时，传统整数PLCRC(超前环节zm中m为整数)将难以满足系统稳定的要求，主要表现在：

1) 设计重复控制器的陷波器时，其谐振频率难以保证在原系统的谐振点上，造成逆变器谐振峰和陷波器难以“完美”对消，可能造成系统不稳定。

2)设计重复控制器超前环节的补偿器时，可能无法找到合适的补偿拍数，造成相位过补偿或欠补偿。

图2为相位补偿环节在采样频率分别为10 kHz、5 kHz和2.5 kHz时的相频特性曲线。由图2可知，不同的采样频率，z的相位随角频率变化的速度不同。因为z=ejωT，T为采样周期，相角θ=ωT=ω/f，则采样频率越小，相角增长越快。超前环节zm中m取整数时在低采样频率下的相位角补偿变快，会对GP(s)造成过补偿或欠补偿，从而使系统鲁棒性变差或不稳定。

图2 3种采样频率下的相位超前补偿环节的相频特性

3 PCLRC的原理

PLCRC系统控制框图如图3所示。PLCRC与传统RC的不同在于被控对象P(z)前引入了补偿环节S(z)，以补偿P(z)的相位滞后以及系统参数变化等引起的系统不稳定。

图3 PLCRC系统控制图

图3中，为了设计S(z)中相位超前环节，将RC内模的延时环节z-N移到前向通道上。其中kr为重复控制增益，Q(z)为增强系统稳定性而设计的零相位低通滤波器或常数。系统的误差表达式为

(3)

则系统的稳定条件为

(4)

由式(4)可知，相位超前补偿环节S(z)、增益kr和Q(z)影响系统稳定。补偿环节S(z)分为相位超前补偿zm、陷波器S1(z)和低通滤波器S2(z)三部分。设计S(z)时，先根据P(z)的幅频特性选取S1(z)和S2(z)，然后根据S1(z)S2(z)P(z)的相频特性选取超前拍次m，使zmS1(z)S2(z)P(z)在中低频段接近于零相位和零增益。

为了设计相位超前补偿环节zm，令

G(z)=S1(z)S2(z)P(z)

则有

S(z)P(z)=zmS1(z)S2(z)P(z)=zmG(z)

(5)

式中G(eiωT)=Mg(eiωT)exp[iθg(eiωT)]， 其中Mg(eiωT)和θg(eiωT)分别为G(eiωT)的幅频特性和相频特性。由于Q(z)为零相位，所以Q(eiωT)=Mq(eiωT)。 由式(4)可得

(6)

对式(6)两边平方后，整理得

(7)

(8)

由于0≤Mq(eiωT)≤1，则式(8)中右边的第一项为非负值，于是kr满足式(9)。

(9)

只要kr满足式(9)，就一定满足式(8)。式(9)成立，则必须满足

(10)

式(9)和式(10)分别给出了参数kr和m的选择范围。

文献[11]指出相位补偿环节对RC系统的整体性能影响最多，因而补偿器S(z)=zmS1(z)S2(z)是重复控制策略设计的重点，其中zm是设计的核心。

在传统相位超前补偿重复控制中，采样频率较高，一般在10 kHz以上，此时为了提高系统稳定性，常采用超前相位补偿环节补偿m拍，m为整数。而当采样频率降低时，超前补偿拍数m可能变为分数，此时传统PLCRC将不能取得良好控制效果。

4 分数相位超前RC的设计

当采样频率降低时，高采样频率下传统PLCRC整数超前补偿环节zm中的m将变为分数。本文将这种控制方法称为分数相位超前重复控制(Fractional Phase Lead Compensation Repetitive Control，FPLCRC)。

FPLCRC主要有3个参数需要设计：增益kr、内模参数Q、分数相位超前补偿环节。

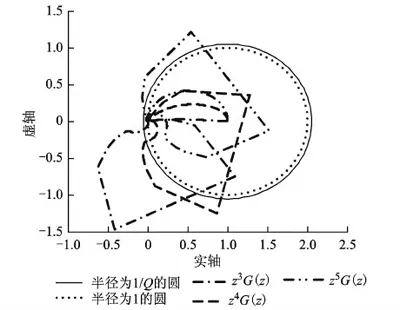
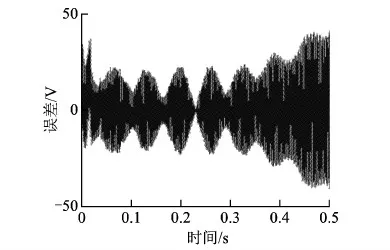
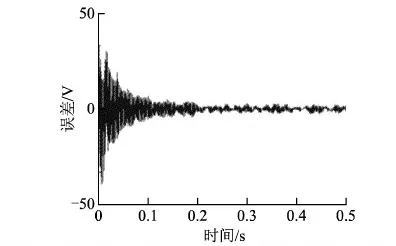
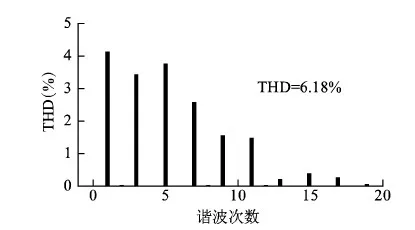
文献[13]认为kr取值范围为0

Q牺牲系统稳态误差来增加系统稳定性，可以为低通滤波器或小于1的常数。根据经验取Q=0.95，系统的稳态误差较小且鲁棒性好[14]。

分数相位超前补偿环节设计分为3步：①陷波器S1(z)设计；②低通滤波器S2(z)设计；③超前拍次m设计。

独立逆变器的滤波器电感L=1.35 mH，电感等效电阻r=0.1 Ω，滤波电容C=60 μF，采样周期T=250 μs(即采样频率f=4 kHz)时，逆变器在不同线性负载下的幅频特性曲线如图4所示。

由图4可知，幅频特性在560 Hz左右存在谐振峰，且不随负载阻值的变化而变化。阻值越大谐振峰越尖锐。显然系统空载时谐振峰最大，此时系统的传递函数为

(11)

采用ZOH方法将其离散化，变为

(12)

图4 逆变器在不同负载时的幅频特性

4.1 陷波器的设计

陷波器的目的是用来抵消系统谐振频率特性的谐振峰。陷波器一般选梳状滤波器，本质为零相位低通滤波器，其表达式为

(13)

由于系统的谐振频率为fr=560 Hz，对应角频率ωr=2πfr=3 518 rad/s。由于z=eiωT=eiθ， 则

(14)

令S1(θ)=0， 解得2cosrθ+a=0。 令a=2， 则rθ=π， 所以

为方便实现，r取整数4。此时，陷波器S1(z)为(z4+2+z-4)/4， 其频率特性为在频率fr附近幅值迅速衰减，其他频率处幅值无衰减或衰减很小，而相频特性为0，不会引入相位滞后。

4.2 低通滤波器的设计

低通滤波器S2(z)用于对高频信号的衰减以增强系统的抗扰动能力。S2(z)引入的相位滞后可用超前环节补偿。通常选用二阶低通滤波器，形式为

(15)

式中：阻尼比ζ选为1；ωn最好选在谐振频率处，由于整流负载会带来奇数次谐波，所以本文中ωn选在4 084 ras/s处，即13次谐波处。此时

(16)

此时，P(z)得到补偿，补偿后的系统传递函数为G(z)=S1(z)S2(z)P(z)，其伯德图如图5所示。由图5可知，补偿后系统的幅频特性得到提高，谐振峰消失了，高频处幅值快速衰减，抑制高频谐波能力增强。补偿引起的相位滞后可用相位超前补偿环节zm改善。

图5 补偿前后系统的bode图

4.3 分数超前环节设计

由式(10)可知，系统的理想情况是θg(eiωT)+mωT=0， 即补偿后的系统zmG(z)的相位为零。根据实际系统，可确定m的范围为3～5。当m分别为3、4、5时，zmG(z)的奈氏曲线如图6所示。

图6 zmG(z)的奈氏曲线(m=3，4，5)

由图6可知，m分别为3、4、5时对应的奈氏曲线都不完全在特征圆(以(1，0)为圆心，1为半径的圆)内。如果m取4和5之间的数，zmG(z)的奈氏曲线可能完全在特征圆内，保证系统稳定。

式(6)中，kr=1，得到

(17)

定义1 如果Qmax表示Q能取得的最大值，式(17)中的Q的稳定裕度为Δ，那么

(18)

Δ的意义在于满足式(18)的所有Q，都能使得系统稳定条件(式(6))成立。且Δ大于零，系统稳定，稳定裕度随Δ的增大而增大；Δ小于零，系统不稳定。

超前补偿环节zm中m为分数时，数字系统无法实现，因此采用拉格朗日插值法利用整数拍次近似分数拍次。对于m为分数的超前环节zm，其N阶拉格朗日插值实现公式为

(19)

式中h(n)为系数，可表示为

(20)

当D→N/2，即插值点D靠近采样数据的中心位置时，插值效果最好[15]；N为阶次，N越大精度越高，但计算量变大，本文中N取5，此时可得到m=4.1～4.9时zm的拉格朗日插值实现。

图幅频特性曲线

根据式(18)可知

(21)

5 仿真及实验结果分析

5.1 仿真

为验证FPLCRC分析的正确性，在Matlab/Simulink环境下搭建仿真平台，参数如表1所示。

表1 系统仿真参数Tab.1 Main parameters of simulation system

图8和图9为逆变器在空载情况下超前环节zm中m分别为4和5时的系统输出误差。图10为相位超前补偿z4.5时的误差响应曲线。

图8 m=4时系统空载输出误差

图9 m=5时系统空载输出误差

图10 m=4.5时系统空载输出误差

可见，空载运行时，在整数相位超前补偿环节m分别为4和5的情况下逆变器输出电压误差发散，系统不稳定，而在分数相位超前补偿环节m为4.5时逆变器输出误差经过约0.2 s变的很小。

图11为分数超前补偿时逆变器在阻性负载下输出电压误差。此时系统稳态误差小于2 V，THD仅为0.95%，而且逆变器由空载状态到阻性负载状态过渡过程中误差在0.05 s内快速收敛至稳定状态。

图11 阻性负载下误差响应

图12和图13分别为逆变器系统接整流负载时，开环控制下逆变器输出电压和电流波形及电压波形的FFT分析。由图13可知，输出电压的THD为6.18%，且3、5、7、9、11等奇数次谐波含量较多。

图12 无重复控制时(整流负载)电压电流波形

图13 无重复控制时输出电压FFT分析

图14和图15分别为FPLCRC时，逆变器输出波形和输出电压的FFT分析。此时，输出电压的THD降为1.28%，且低次谐波明显得到抑制。

图14 FPLCRC(整流负载)电压电流波形

图15 FPLCRC(整流负载)输出电压FFT分析

5.2 实验

为进一步验证FPLCRC理论分析的正确性及有效性，搭建了基于TMS320F2812的数字处理器的单相逆变器实验样机。参考电压幅值100 V，母线电压200 V，整流负载电容1 000 μF，电感0.1 mH，电阻100/6 Ω。

空载情况下，FPLCRC闭环控制逆变器输出电压波形如图16所示，THD为1.94%。

阻性负载情况下，FPLCRC逆变器闭环输出电压电流波形如图17所示。

整流负载逆变器输出波形带来奇次谐波，引起输出电压波形畸变。逆变器开环无重复控制时，其输出电压电流波形如图18所示，输出电压波形波峰处有明显凹陷，13次及以下奇次谐波大量存在。输出电流波形为间断的脉冲状。

图16 空载情况下FPLCRC逆变器输出波形

图17 阻性负载情况下FPLCRC逆变器输出波形

图18 逆变器开环控制输出波形

为减小非线性负载引起的输出电压波形畸变，逆变器加入相位超前补偿重复控制。图19和图20为相位超前补偿拍数m分别为4和5时，逆变器输出波形。

图19 m=4时逆变器输出波形

图20 m=5时逆变器输出波形

由图19和图20可知，由于实验系统模型与理想模型存在参数误差，逆变器系统在整数PLCRC下是稳定的。尽管此时的电压波形比无重复控制时有所改善，但逆变器输出电压波形仍然畸变较大。

图21为加入FPLCRC后逆变器输出电压电流波形。由图可知，采用分数相位超前补偿重复控制后，逆变器输出电压波形明显改善，波形畸变率明显减小，各次谐波含量大幅降低，THD=3.27%。

图21 m=4.5时逆变器输出波形

由仿真及实验结果可知，无论线性负载还是非线性负载，采用FPLCRC时低次奇次谐波大大降低，达到了理想的控制效果。

6 结论

针对低采样频率时整数拍数超前重复控制导致控制系统不稳定的问题，提出了一种改进的分数相位超前重复控制策略。引入了分数相位超前补偿环节，将相位超前补偿拍数由传统只能为整数的情况扩大至分数。详细分析了分数相位超前补偿原理，并给出了控制器的设计过程。仿真和实验结果验证了所提出控制策略能够提高系统稳定性，并能有效抑制整流负载产生的奇次谐波。

[1] Jiang S，Cao D，Li Y，et al.Low THD，fast-transient，and cost-effective synchronous-frame repetitive controller for three-phase UPS inverters[J].IEEE Transactions on Power Electronics，2012，27(6)：2994-3005.

[2] Escobar G，Martinez P，Leyva-Ramos J，et al.Repetitive-based controller for a UPS inverter to compensate unbalance and harmonic distortion[J].IEEE Transactions on Industrial Electronics，2007，54(1)：504-510.

[3] 黄朝霞，邹旭东，童力，等.基于极点配置和重复控制的电流型单相动态电压调节器[J].电工技术学报，2012，27(6)：252-260. Huang Zhaoxia，Zou Xudong，Tong Li，et al.Research on current control mode single-phase dynamic voltage regulator based on pole-assignment and repetitive control[J].Transactions of China Electrotechnical Society，2012，27(6)：252-260.

[4] 宫金武，查晓明，陈佰锋.一种快速重复控制策略在APF中的实现和分析[J].电工技术学报，2011，26(10)：110-117. Gong Jinwu，Zha Xiaoming，Chen Baifeng.Analysis and realization of a fast repetitive controller in active power filter system[J].Transactions of China Electrotechnical Society，2011，26(10)：110-117.

[5] Ye Yongqiang，Zhang Bin，Zhou Keliang，et al.High-performance cascade type repetitive controller for CVCF PWM DC-AC converter：Analysis and design[J].IET Electrical Power Applications，2007，1(1)：112-118.

[6] 王斯然，吕征宇.LCL型并网逆变器中重复控制方法研究[J].中国电机工程学报，2010，30(27)：69-75. Wang Siran，Lü Zhengyu.Research on repetitive control method applied to grid-connected inverter with LCL filter[J].Proceedings of the CSEE，2010，30(27)：69-75.

[7] 陈东，张军明，钱照明.一种具有频率变化适应性的并网逆变器改进型重复控制方法[J]，电工技术学报，2014，29(6)：64-70. Chen Dong，Zhang Junming，Qian Zhaoming.An improved repetitive control scheme for grid-connected inverter with frequency-varying adaptability[J].Transactions of China Electrotechnical Society，2014，29(6)：64-70.

[8] Zhang Bin，Zhou Keliang，Wang Danwei.Multirate repetitive control for PWM DC/AC converter[J].IEEE Transactions on Industrial Electronics，2013，61(6)：2833-2890.

[9] Dannehl J，Wessels C，Fuchs F W.Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL filters[J].IEEE Transactions on Industrial Electronics，2009，56(2)：380-388.

[10]Hoffmann N，Fuchs F W，Dannehl J.Models and effects of different updating and sampling concepts to the control of grid-connected PWM converters-A study based on discrete time domain analysis[C].Proceedings of the 2011-14th European Conference on Power Electronics and Applications，Birmingham,2011.[11]Ye Yongqiang，Zhou Keliang，Zhang Bin，et al.High-performance repetitive control of PWM DC-AC converters with real-time phase-lead FIR filter[J].IEEE Transaction on Circuit and System(Ⅱ)，2006，53(8)：768-772.[12]Zhang B，Wang D，Zhou K，et al.Linear phase lead compensation repetitive control of a CVCF PWM inverter[J].IEEE Transactions on Power Electronics，2008，55(4)：1595-1602.

[13]Longman R.Iterative learning control and repetitive control for engineering practice[J].International Journal of Control，2000，73(10)：930-954.

[14]Zhang Kai，Kang Yong，Xiong Jiang，et al.Direct repetitive control of SPWM inverter for UPS purpose[J].IEEE Transactions on Power Electronics，2003，18(3)：784-792.

[15]Laakso T，Välimäki V，Karjalainen M，et al.Splitting the unit delay tools for fractional delay filter design[J].IEEE Signal Processing Magazine，1996，13(1)：30-60.

Application of Improved Repetitive Control Scheme to Inverter with Low Sampling Frequency

ZhaoQiangsong1,2YeYongqiang1XuGuofeng1ZhuMingzhe1PanXue1

(1.College of Automation Engineering Nanjing University of Aeronautics &AstronauticsNanjing 210016 China 2.School of Electronic Information Zhongyuan University of Technology Zhengzhou 450007 China)

For the less effectiveness of conventional control methods，this paper proposes the fractional phase lead compensation repetitive control (FPLCRC) scheme.At the basis of analyzing the problems of conventional repetitive control at low sampling frequency，the principle that phase lead compensation can improve the stability of inverter is provided.The notch filter，the low pass filter，and the fractional phase lead compensator are designed，respectively to meet the requirement of the inverter stability and the steady error.Fractional phase lead compensator can be implemented by Lagrange interpolation.MATLAB/Simulink is the model and simulation platform and an inverter experimental platform is used to validate the effectiveness of the proposed control strategy.

Low sampling frequency，inverter，repetitive control，fractional phase lead compensation，Lagrange interpolation

国家自然科学基金(61473145)、中央高校基本科研业务费专项资金和江苏省研究生培养创新工程(KYLX_0279)、河南省高等学校重点科研项目计划(15A413020)资助。

2014-12-22 改稿日期2015-08-02

TM464

赵强松 男，1982年生，博士研究生，研究方向为逆变器控制，重复控制理论。

叶永强 男，1972年生，教授，博士生导师，研究方向为电力电子控制及应用控制理论。(通信作者)