匝道桩基施工对地铁结构变形的数值分析

朱红霞，周文权，梁 桥

(1. 武汉地铁集团有限公司, 武汉 430077; 2.湖南工程学院 建筑工程学院, 湘潭 411104)



匝道桩基施工对地铁结构变形的数值分析

朱红霞1，周文权2，梁 桥2

(1. 武汉地铁集团有限公司, 武汉 430077; 2.湖南工程学院 建筑工程学院, 湘潭 411104)

针对番禺新光快速路匝道桩基穿越既有地铁工程附近土层，通过建立三维有限元模型，分析了桩基施工过程对于既有地铁结构变形的影响.通过计算分析可知，桩基施工顺序对隧道结构的变形、轴力和弯矩的影响都较小，说明桩基施工对隧道结构没有明显影响.

桩基；地铁结构；隧道；数值分析

0 引 言

近年来，随着国民经济的迅速发展，城市化进程不断加快，我国交通事业也得到了迅猛的发展[1,2]．以公路为主的地面交通网络迅速发展，修建里程数不断增加.同时，为缓解道路拥堵，解决交通和社会协调发展的问题，在一些经济发达大中型城市逐步形成了以地下铁道为主的现代城市轨道交通格局[3].由于城市用地紧张，地铁工程往往修建在公路下方，导致上部构筑物和下部隧道工程出现相互影响的问题，如不处理好将对整个交通工程的安全带来不利的影响[4,5].本文以番禺新光快速路匝道桩基施工为背景，采用数值模拟的方法就桩基施工对近距离既有地铁结构变形的影响进行分析，可为将来类似工程的设计、施工提供参考.

1 工程概况

拟建新光快速路南大路立交南侧匝道工程位于番禺区大石礼村，其中该工程的ND、NF匝道由南大路开始，沿新光快速路两侧并行一段距离后与新光快速路既有路基相接.已建地铁三号线“大石-汉溪”区间盾构隧道由北向南从新光快速路下方穿过.ND、NF匝道由桥梁和路基组成，两条匝道各设一座桥梁，基础采用直径1.2 m 的钻孔灌注桩，采用旋挖钻机成孔，桩长约25.0～32.0 m，桩底标高约-13.46～-20.32 m；位于地铁上方的路基基底采用厚约3.0 m抛石挤淤或浅层换填的处理方式.经核查，地铁盾构隧道结构外侧与ND匝道桥墩基础桩之间的最小水平净距离约3.88 m，为桩基施工控制的关键位置，相应范围内地铁隧道结构底与路基基底之间的最小垂直距离约8.2 m，相应范围内地铁隧道结构顶标高约-4.21 m，底标高约-10.2 m.该工程线路和桩基的平面布置如图1所示.

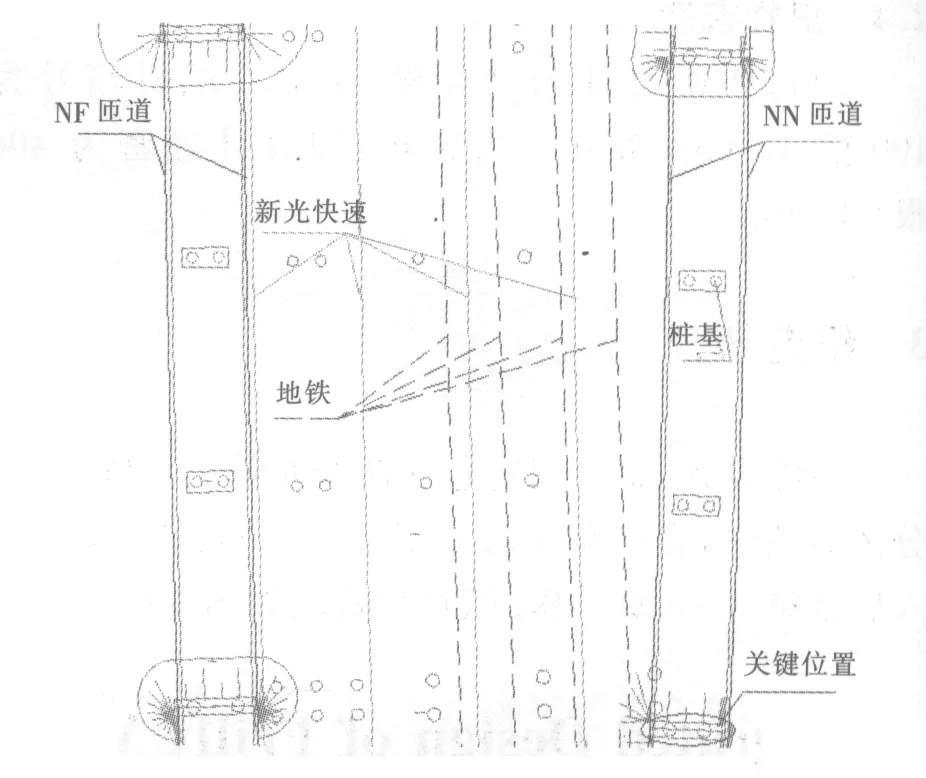
图1 线路及桩基相对位置的平面布置图

运营中的既有地铁三号线是广州市的重要交通生命线，安全性要求高.因此，在该匝道基础工程施工期间，了解匝道基础工程施工阶段地铁结构及周边地层动态变化，明确基础工程施工对地铁影响程度，把握施工过程中地铁结构所处的安全状态，对安全管理，避免出现工程安全事故无疑具有重要的现实意义.

2 建立几何及材料模型

桩基础与地铁隧道距离最近的位置，其基础施工对地铁的影响势必最大，此处是施工控制的关键位置.因此，本文对此关键位置进行有限元计算分析.采用Plaxis 3D Tunnel进行模拟计算.

此位置处有两根单桩，地面高程为8.7 m ，稳定水位深2.5 m ；两根桩中心间距5.0 m，桩径1.2 m，桩底标高-20.315 m；地铁隧道直径6.0 m，顶高程取-4.2 m,底高程取-10.2 m，管片厚度30 cm，地铁上下行线的水平净间距为7.0 m，竖向高程相同.为便于模拟，将圆形桩断面等效为矩形断面，采用等效刚度法，令两种断面情况下混凝土模量相等.根据面积相等，则式中，d为桩径；l为换算的方形断面边长.

(1)

由式(1)得到等效的桩基方形断面边长l为1.063 m.

根据现场勘察资料，模拟采用的岩土体物理力学参数值参见表1，强风化的泥质粉砂岩透水性比较好，可以认为在整个施工过程中都是排水的，但因地铁隧道位于此岩土层中，为了考虑地铁结构与此岩土层存在的软弱界面，在此另设一层泥质粉砂岩，设定其界面强度折减因子Rinter=0.8，其他参数值与表1中的强风化泥质粉砂岩相同；粉质粘土位于地下水位以下，透水性较差，在桩基钻孔施工中，钻孔速度很快.因此在成孔施工阶段，将粉质粘土考虑为不排水状态更符合工程的实际情况，故本文另定义一粉质粘土层，材料类型为不排水，其他参数值与表1中粉质粘土相同，用以模拟成孔时粉质粘土层的不排水性质.桩基混凝土强度等级C25，物理力学参数取值参见表1；另外，本工程两相邻桩基的中心间距为5 m，为了防止后施工桩基施工对先施工已灌注混凝土桩基产生过大的不利影响，在已浇注的桩基混凝土强度达到75%设计强度的时候再施工另一临近桩基，因此，定义另一混凝土材料，其弹性模量是表1中混凝土的75%，即2.1*107 kN/m2，用以模拟混凝土强度达到75%时的情况，其他参数取值与表1中混凝土材料相同.地铁衬砌混凝土强度等级C50，用弹性板来模拟，材料性质如表2所示.

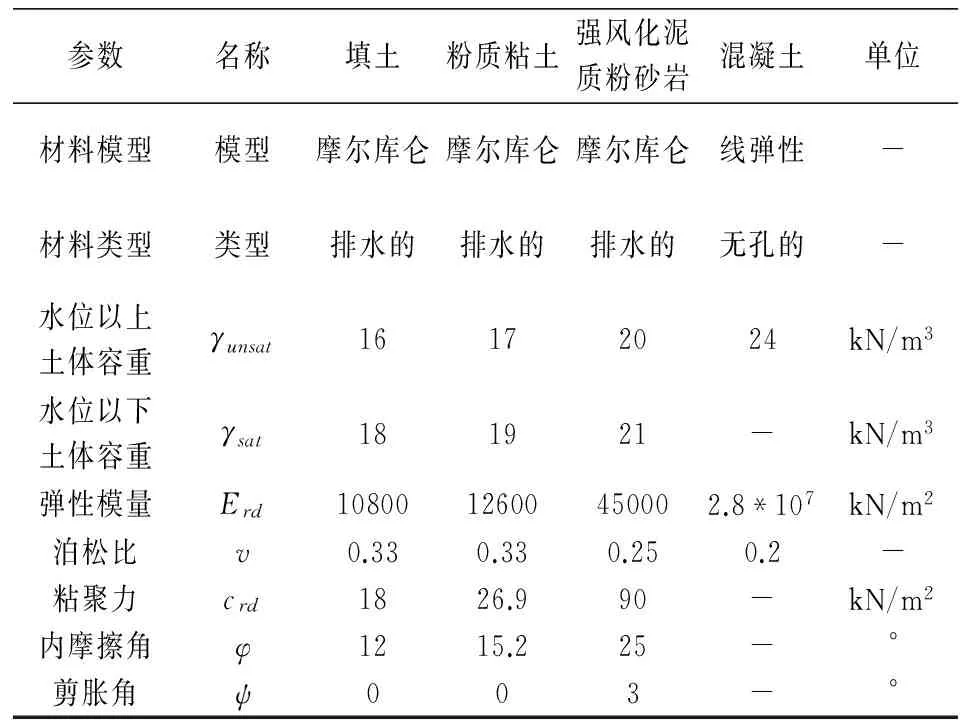
表1 岩土体和混凝土材料性质

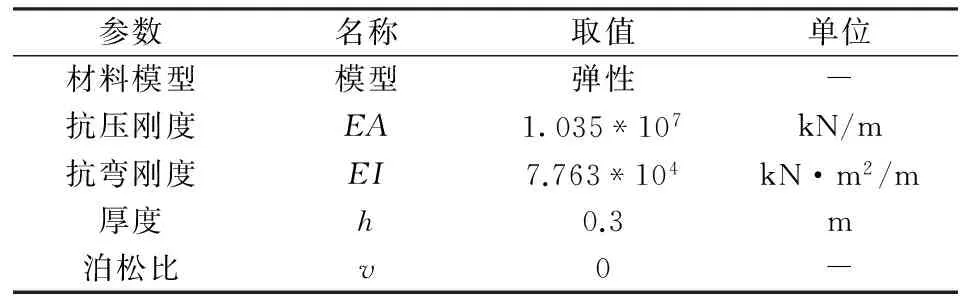
表2 地铁隧道衬砌材料性质

按照上述建立的此处横断面的几何和材料模型如图2所示，此模型长50 m，深度方向深40 m；划分单元后的三维几何材料模型如图3所示,采用15节点单元;考虑此模型在沿地铁运行方向的对称性，图3中所示只取了一半模型.借助于合适的边界条件来进行模拟，即桩基中心轴线对应的隧道横断面沿一个方向拉伸建立三维模型，在此三维模型中，沿地铁方向的长度为15 m，此方向桩基的等效边长为原等效边长的一半即0.532 m，需要说明的是，在未钻孔前，模型中所示的桩基位置的材料仍是对应的岩土体.此模型边界采用标准固定边界约束，即在模型底部施加完全固定约束，而模型侧面施加滑动约束，即在深度方向可以自由发生变形.隧道衬砌及桩基边缘是发生变形的关键部位，故对隧道内部开挖的土体及桩位置处的土体在生成单元时进行了网格加密.

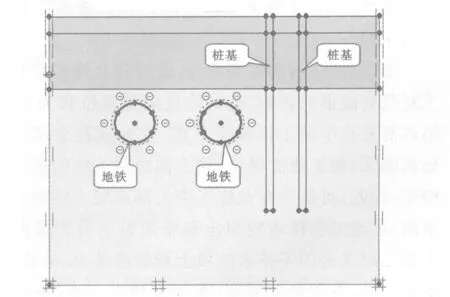
图2 横断面模型图

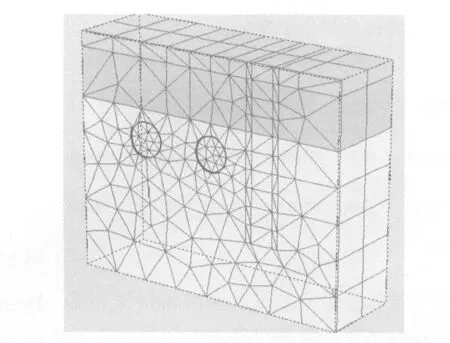
图3 三维模型图

3 初始条件

建立划分单元的三维几何材料模型后，就可以生成初始条件，即在地下水和土体自重作用下土体中水压力和应力的生成，因土体在自重作用下已经历漫长的过程，固结已经完成，所以在生成初始条件时，所有的土体材料都是排水的，而结构在这时是没有被激活或不存在的.

4 施工阶段的计算划分

此过程采用分部施工的模拟方法，下一阶段的计算基于上一阶段计算完成后的土体和结构应力状态，采用增量法计算模拟.

第1阶段：地铁修建.冻结两条隧道内的土体模拟开挖，并激活地铁衬砌结构模拟衬砌修建，为了很好地模拟地铁结构与其周围岩土体的相互作用，在衬砌外侧设置了界面单元，因此，需要更改地层土的材料性质，将底层土的材料更改为泥质粉砂岩(Rinter=0.8).地铁隧道修建完成至今已有很长的时间，因此，所有岩土体的材料类型均为排水的，但隧道内的土体已开挖，应设为干类组材料.最后，重新生成孔隙水压力.

第2阶段：右侧桩基成孔.此过程是模拟桩基施工对既有隧道的影响，故此阶段应重置位移为0.冻结右侧桩孔中的土体模拟开挖，桩基成孔采用旋挖钻机施工，施工速度很快，而上部两层土体的透水性较差，因此，可认为在此施工中上部两层土体是不排水的，可通过将排水的填土和粉质粘土分别修改为上述已定义过的不排水的填土和粉质粘土.另外，旋挖施工中，有少量的泥浆，重度要稍大于水，故在冻结桩孔中土体的同时，在孔壁施加重度为10.5 kN/m3的液体压力，在地面处液体压力为0，则在孔底液体压力则为304.5 kN/m3.最后，重新生成孔隙水压力,如图4所示.

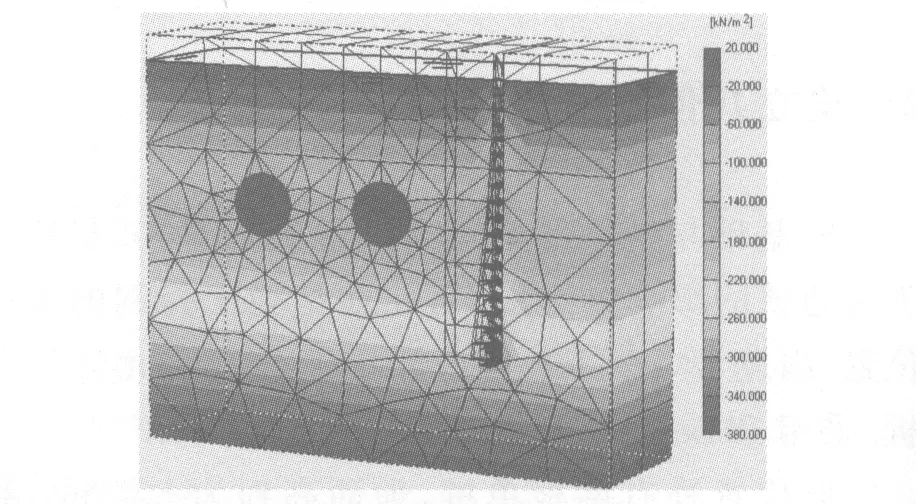
图4 第2阶段孔隙水压分布

第3阶段：右侧桩孔灌注混凝土.在这一阶段，将原施加于孔壁的液体重度修改为24 kN/m3来模拟灌入的流体混凝土.

第4阶段：右侧桩基混凝土达到75%设计强度.在这一阶段，激活右侧桩孔中的土体材料并将其修改为已定义的75%设计强度的混凝土材料，并将其设为不含水的干类组材料.重新生成孔隙水压力.

第5阶段：在右侧桩基混凝土达到75%设计强度时进行左侧桩基成孔.这样可以避免左侧桩基施工对右侧桩基产生过大的影响.冻结左侧桩孔中的土体材料模拟其开挖并在孔壁施加重度为10.5 kN/m3的液体压力.设定完成后，重新生成孔隙水压力.

第6阶段：左侧桩孔灌注混凝土.这一过程与第3阶段右侧桩孔灌注混凝土的模拟相同.

第7阶段：混凝土达到设计强度等级.这一阶段，混凝土凝固达到设计强度，因此，将桩孔位置处的土体激活并将其修改为前述已设定好的混凝土材料，同时将混凝土材料设定为不含水的干类组材料，重新生成孔隙水压力.另外，混凝土从灌注到凝固并达到设计强度，历经时间较长，应认为所有材料都是排水的，因此，这一阶段将上部两层土体的材料再次修改为排水的.最后，重新生成孔隙水压力.

为了对比两根桩不同施工顺序对地铁变形的影响，对先施工左侧桩基再施工右侧桩基的施工方案也进行了模拟，模拟的阶段划分与先施工右侧桩基的相同，也分为7个施工阶段.

5 模拟计算结果及分析

将先施工右侧桩基的施工方案定为方案1，先施工左侧桩基的定为方案2.

因右侧隧道距离桩基位置最近，桩基的施工对其的影响比对左侧隧道的要大，所以取右侧隧道为分析对象.不同施工阶段结束时桩基与地铁最近位置处的横断面上(此横断面上地铁隧道距离桩基最近，为最危险断面)右侧隧道结构的变形见表3.

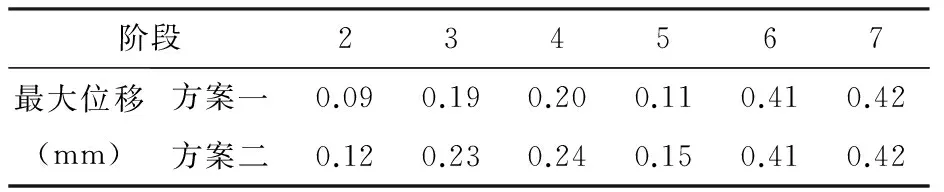
表3 各个施工阶段结束时右侧隧道结构的累计最大位移

每个施工阶段的累计最大位移反映了桩基施工对隧道结构的影响程度，因此，将每个施工阶段结束时的累计最大位移统计如表3所示，其累计最大位移大小的变化如图5所示(因本文为分析桩基施工对隧道结构变形的影响，地铁结构已经使用，所以第二阶段开始的位移设为0).

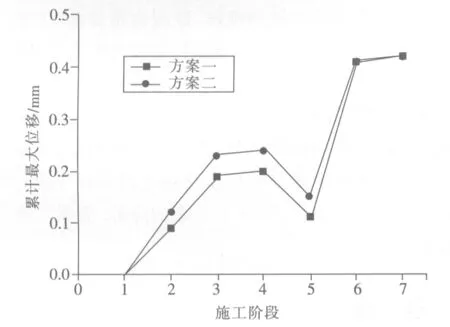
图5 各个施工阶段结束时右侧隧道结构的累计最大位移

由图5及表3中可以看出：

(1)方案二的施工引起的隧道结构累计最大位移在施工中稍大于方案一，但桩基施工完成后两施工方案引起的隧道结构位移相同.

(2)第4阶段和第7阶段均是混凝土材料强度的形成时期，此阶段对隧道结构的位移影响很小，两阶段引起的隧道位移两种方案均为0.01 mm，近似可以认为第4阶段和第7阶段的施工对隧道结构变形没有影响.

(3)第2阶段方案一的累计位移略大于方案二的累计位移，说明桩基与隧道越近，其开挖对隧道结构的变形影响越大.

(4)针对方案一，在右侧桩基成孔后即第2阶段完成时，隧道结构产生向桩基位置的位移，这是因为桩孔开挖导致了隧道右侧应力释放的缘故，浇注混凝土后即第3阶段隧道结构又发生背离桩基方向的位移，是因为液体混凝土的重度大于原桩位处土体材料的，对孔壁土体产生了挤压所造成的.而在第4阶段完成时，混凝土强度达到其设计强度的75%这一过程引起的隧道结构变形只有0.01 mm,对隧道结构的变形几乎没有影响.第5阶段开挖左侧桩基又因隧道右侧应力释放而使隧道向桩基位置产生了回移，但此阶段累计位移依然背离桩基方向，第6阶段左侧桩基灌注混凝土又因混凝土对孔壁的挤压作用而使隧道产生背离桩基位置的位移，第7阶段混凝土强度上升期对隧道结构的变形影响甚微.在第7阶段完成时即两桩基混凝土达到设计强度是隧道结构累计位移达到最大0.42 mm.同样，方案二的施工呈现与方案一同样的规律，最大累计位移也发生在第7阶段也为0.42 mm.

(5)总体看来，两种施工方案对隧道结构变形的影响都很小，隧道产生的最大位移只有0.42 mm.

对于隧道内力，施工过程中隧道结构产生最大内力的阶段应为控制阶段，用以判断对隧道结构的影响程度，两种方案产生的最大累计轴力均发生在第7阶段，如图6所示.而产生的最大累计弯矩均发生在第2阶段，如图8所示.各个施工阶段最大累计轴力的变化情况如表4和图7所示；最大累计弯矩的变化情况如表5和图9所示.

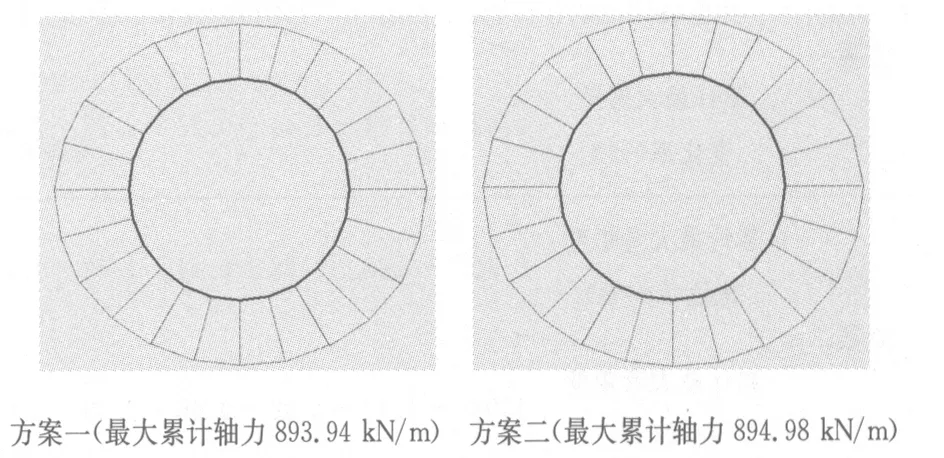
方案一(最大累计轴力893.94 kN/m) 方案二(最大累计轴力894.98 kN/m)

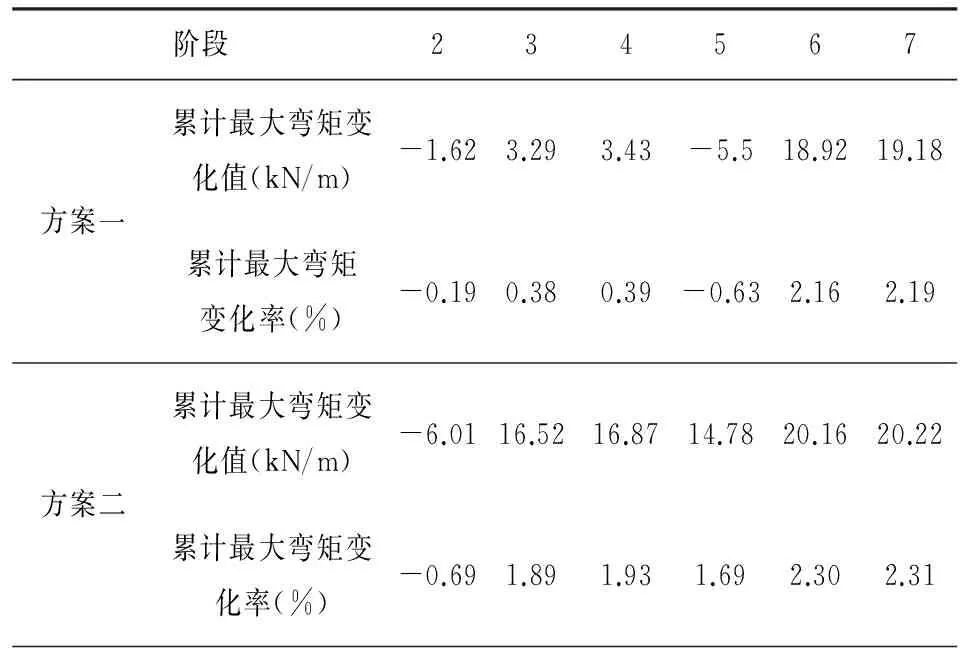
阶段234567方案一累计最大弯矩变化值(kN/m)-1.623.293.43-5.518.9219.18累计最大弯矩变化率(%)-0.190.380.39-0.632.162.19方案二累计最大弯矩变化值(kN/m)-6.0116.5216.8714.7820.1620.22累计最大弯矩变化率(%)-0.691.891.931.692.302.31

注明：第1阶段结束时隧道结构最大轴力为874.76 kN/m 负值代表增加，正值代表减小

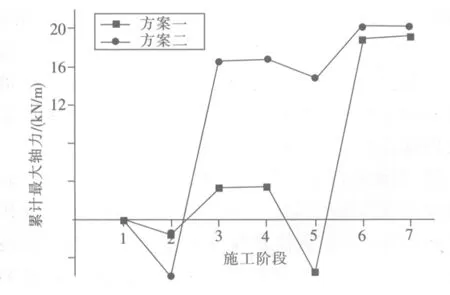
图7 各个施工阶段结束时右侧隧道结构的累计最大轴力变化(相对于第1阶段)

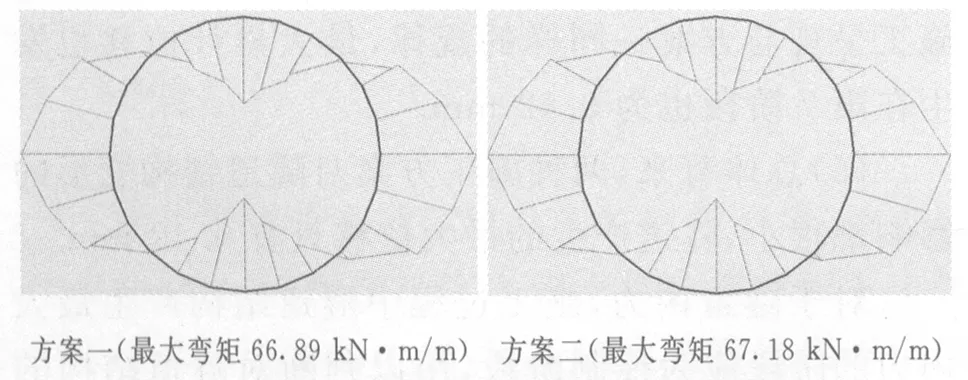
方案一(最大弯矩66.89 kN·m/m) 方案二(最大弯矩67.18 kN·m/m)

阶段234567方案一累计最大弯矩变化值(kN/m)0.41-0.94-0.94-0.15-1.71-1.64累计最大弯矩变化率(%)0.62-1.41-1.41-0.23-2.57-2.47方案二累计最大弯矩变化值(kN/m)0.70-0.98-0.88-0.44-1.72-1.73累计最大弯矩变化率(%)1.05-1.47-1.32-0.66-2.59-2.60

注明：第1阶段结束时隧道结构最大弯矩为66.48 kN·m/m，负值代表增加，正值代表减小

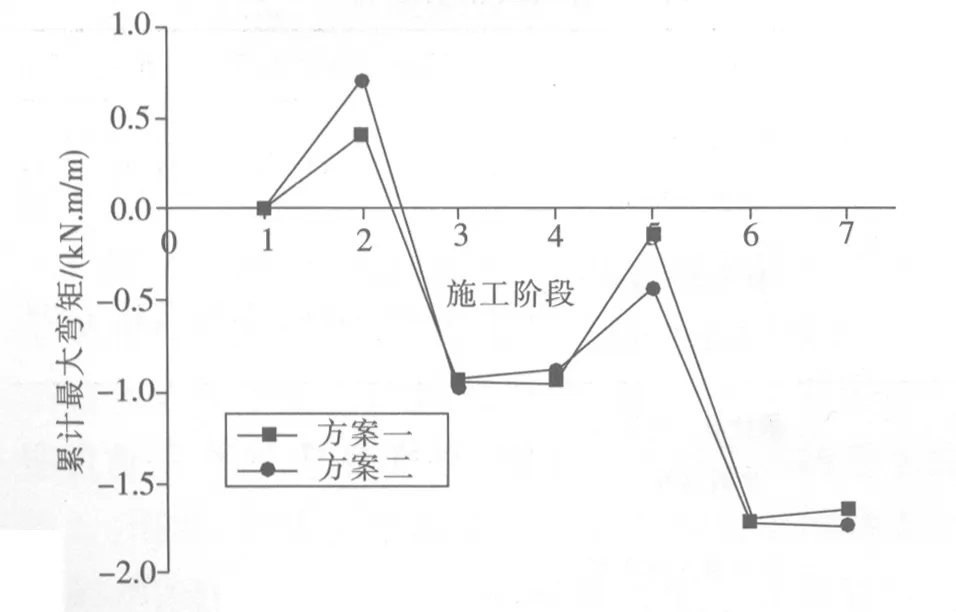
图9 各个施工阶段结束时右侧隧道结构的累计最大弯矩变化(相对于第1阶段)

从图6～图9以及表4和表5我们可以看出：

(1)方案二引起的隧道累计最大轴力和累计最大弯矩要略大于方案一.但两种方案引起的累计轴力和累计弯矩变化均很小，方案一和方案二引起的最大累计轴力变化率分别为2.19%和2.31%，最大累计弯矩变化率分别为0.62%和1.05%.并且产生最大累计轴力的施工阶段(第7阶段)弯矩的变化率呈现负值(意味着比第一阶段的弯矩要小)，而产生最大累计弯矩的阶段(第2阶段)轴力的变化率呈现负值，因此可以认为两种方案对隧道结构内力的影响均很小.

(2)针对方案一，轴力在开挖右侧桩孔时减小，这是因为隧道附近土体卸载造成的，而在浇注时又增加，则是因为液体混凝土对隧道周围土体起到了再加载的效应，而混凝土强度上升期隧道轴力变化极其微小，可以近似认为没有影响，紧接着施工左侧桩基时也呈现处同样的规律，原因也是如此.方案二轴力的变化规律与方案一相同，原因与方案一相同.

(3)弯矩的变化规律正好与轴力相反，对于方案一，在开挖桩孔时增加，这是因为开挖桩孔引起了隧道向着桩基方向的位移，导致了弯矩的增加，而灌注混凝土对孔壁土体产生挤压使隧道回移并在背离桩基方向产生了位移，导致了弯矩的降低.方案二也是如此.

6 结 论

由上述数值模拟计算和分析，可以得到如下结论：

(1)方案一在施工过程中对隧道结构变形的影响要略小于方案二，但两种方案最终对隧道结构变形的影响程度相同，均使隧道结构产生了0.42 mm的累计最大位移，对隧道结构变形的影响较小.

(2)桩基与隧道的距离不同，开挖桩孔时引起的隧道结构变形也不同，距离越小，开挖引起的隧道结构变形也越大.

(3)两种方案所引起的隧道结构变形随施工阶段变化的原因是挖孔和浇注混凝土对隧道周围土体产生了卸载和加载效应所引起的.

(4)两种施工方案对隧道结构内力的影响较小.方案一和方案二引起的最大累计轴力变化率分别为2.19%和2.31%，最大累计弯矩变化率分别为0.62%和1.05%.并且产生最大累计轴力的阶段弯矩的变化率呈现负值，产生最大累计弯矩的阶段轴力的变化率同样呈现负值.

(5)两种施工方案累计轴力随施工阶段的变化规律和累计弯矩相反.累计轴力和累计弯矩的变化均是因为挖孔和浇注混凝土对隧道周围土体产生了卸载和加载效应所引起的.

(6)总体看来，无论哪种施工方案，对隧道结构的变形、轴力和弯矩的影响都较小，说明桩基施工对隧道结构的影响比较小.

[1] 孟 光，张建新，伍廷亮.地铁荷载作用下隧道土体变形的数值模拟[J].天津城市建设学院学报，2012,18(2):103-107.

[2] 胡海波.地铁隧道穿越既有桥梁及地裂缝带施工的现场监测与数值模拟研究[D].中南大学硕士论文，2009.

[3] 王庆国，孙玉永.旋喷桩加固对控制盾构下穿铁路变形数值分析[J].地下空间与工程学报，2008,4(5):860-864.

[4] 于 宁，朱合华.盾构隧道施工地表变形分析与三维有限元模拟[J].岩土力学，2004,25(8):1330-1334.

[5] 王建秀，田普卓，付慧仙，等.基于地层损失的盾构隧道地面沉降控制[J].地下空间与工程学报，2012,8(3):569-576.

Numerical Analysis of Subway-structural Deformation for Ramp Pile Foundation Construction

ZHU Hong-xia1,ZHOU Wen-quan2,LIANG Qiao2

(1.Wuhan Metro Group Co., Ltd，Wuhan 430077, China;2.School of Architecture and Civil Engineering, Hunan Institute of Engineering, Xiangtan 411104, China)

Based on the ramp piles of Xin-guang freeway in Pan-yu passing the soil layer near the existing subway project, a 3D- FEM model is built to analyze the effects of pile construction process for the existing metro structural deformation. Analysis result shows that the deformation, axial force and bending moment of existing tunnel structure are small for pile foundation construction sequence.

pile; subway structure; tunnel; numerical analysis

2014-09-16

湖南省高校科研项目(12C0621).

朱红霞(1970-),男，高级工程师，硕士，研究方向：地铁工程.

TU455.43

A

1671-119X(2015)01-0070-06