抗野值强跟踪Kalman 滤波在风场估计中的应用*

李 阳，孔 毅，赵现斌

(1.解放军理工大学 气象海洋学院，江苏 南京211101;2.中国人民解放军94994 部队，江苏 南京210017)

0 引 言

随着气象无人机技术的发展，利用无人机搭载皮托静压管进行空中风［1］探测日益引起国内外关注。皮托静压管测风是把无人机作为探测平台［2］，搭载机载气象传感器和数据采集装置进行风速测量。这种大区域、长时间、连续风场探测方法在航天器发射与返回、重要武器试验、战场气象测量、恶劣天气监测、龙卷风近距环境探测监视等应用中具有独特的作用和优势。

在高空风场探测过程中，由于受传感器工作状态、环境杂波等因素的影响，量测数据中经常存在一些异常值。因此，风场数据处理方法是无人机测风的一项重要内容，对提高测风精度具有重要意义。当前常使用Kalman滤波算法对风场数据进行处理，但其过于依赖系统噪声和量测噪声的统计特性，且缺乏对测量数据过失误差的抗扰性和对传感器突发性故障的容错能力［3］，降低了滤波精度和抗野值能力，容易造成系统的不稳定。

本文针对气象无人机的测风特点和Kalman 滤波在数据处理中的局限性，将强跟踪Kalman 滤波和抗野值算法应用于无人机探测数据处理中，达到抑制滤波发散，提高滤波精度的目的。

1 滤波算法

1.1 Kalman 滤波算法

Kalman 滤波是典型的最小方差(MMSE)估计方法，采用 递归技术，利用k－1时刻状态值给出k的预测值，并保证该均方误差最小。建立离散系统模型

状态方程

量测方程

上述模型中，Xk为状态向量，Zk为观测向量，φk|k－1为k－1 时刻到k 时刻的状态转移矩阵，Hk为量测矩阵，Wk－1和Vk分别是均值为零，方差为Qk－1和Rk且相互独立的过程噪声和量测噪声。由于Kalman 滤波是一个带回馈的估计方法，可将其分为时间更新和量测更新两个阶段。

时间更新方程:

状态一步预测

一步验前误差方差阵

量测更新方程:

增益阵

滤波方程

验后误差方差阵

新息序列

上述方程未提供相关噪声的估计模型，且无人机测风受噪声影响较大，因此，需对系统噪声和量测噪声进行分析。由于系统干扰存在稳定性，可设系统噪声方差Q 为定值;量测噪声受周围环境的影响较为明显，需对量测噪声方差R 在线估计。利用Sage-Husa 自适应滤波［4］，得到量测噪声方差

1.2 改进的强跟踪Kalman 滤波算法

强跟踪Kalman 滤波［5］是在Kalman 滤波理论的基础上提出的，为保证滤波器的可靠收敛，在一步验前误差方差阵中引入可在线计算的时变渐消矩阵［6］。该方法在风场突变时具有很强的跟踪能力，同时对噪声统计特性的敏感性也较低。因此，将式(4)修改为

其中

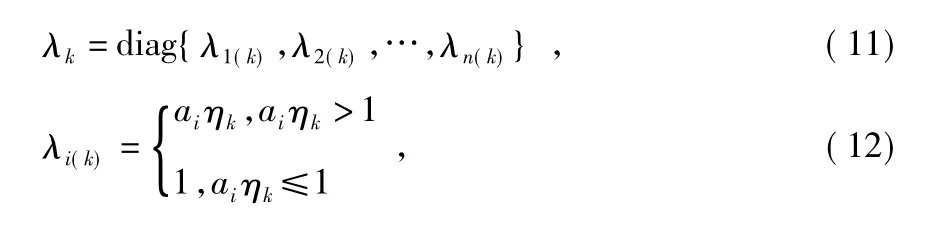
应用统计方法，可用算术平均值将v0(k)近似表示

式中 各项加权系数均为1/k，但风场估计中应该强调新进信息的作用，因此，可以改变因子，使和式中的各项乘以不同的加权系数。应用指数加权方法，新建加权系数μi，并使其满足

由等比数列求和公式可推导出

其中，a 为遗忘因子，式(15)中的和式各项乘以加权系数μk－i，代替原来的1/k，得到v0(k)近似估计算法

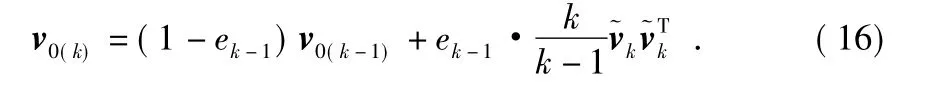
1.3 抗野值修正算法

带有野值的数据样本往往会使Kalman 滤波器对系统的状态预报修正错误，使滤波结果发生偏移，以往常采用3δ 准则进行野值判别，但其判别尺度把握不灵活且修正值的准确度不高。为了提高抗野值能力，保证滤波精度，文献［7］提出了一种利用新息序列加权的方法来消除野值影响的方法。当量测数据不包含野值时，滤波器能够有效利用新息，同时对量测噪声进行在线估计;当量测数据中存在野值时，能克服其不利影响，尽可能还原系统真实状态。抗野值算法如下

其中

式(18)为压缩影响函数;式(19)为权矩阵;式(20)为选取的门限常数序列。此外，λk为矩阵的最大特征值，为以χ2(m)分布置信度为(1－α) ×100%的上分位点，通常情况下α 取0.05 或0.025，m 为量测数据Zk的维数。上述模型抗野值原理是通过引入压缩影响函数，改变野值的影响权重，抑制野值带来的异常新息，达到抗野值的目的。

2 抗野值自适应滤波算法

自然风大致可分解为定常风、紊流、风切变和突风四个分量［8］。通常情况下，在风场探测系统中，将风速表示成定常风和紊流之和，并在此基础上叠加量测噪声，一旦量测值中出现野值或滤波发散时，误差协方差阵都将无界，此时实际的新息往往比理论预计的大很多倍。实际的新息用vk表示，理论预计误差的新息用新息序列协方差阵E［vk来描述，。因此，野值是否存在或滤波是否发散的依据为

式中 κ 为判别因子，其大小往往取3 或4。当其成立时，量测值Zk为正常量测值，直接采用引入Sage-Husa 的Kalman 滤波进行最优估计;反之，说明量测值Zk为野值或滤波发散。设置连续野值门限值，当连续的野值数多于该门限值或滤波发散时采用改进的强跟踪Kalman 滤波算法;当存在少数野值时采用抗野值修正算法。抗野值强跟踪Kalman 滤波算法流程如图1。

3 测风实验与结果分析

3.1 风场模型建立

飞行仿真中，定常风用低频风模型［9］描述，紊流场由基于空间相关函数的方法［10］建立，风切边、突风等在内的大气扰动分量直接叠加到量测噪声上，本文不予单独考虑，建立风场模型

式中 VD，VW，y 分别为定常风速、紊流风速和量测风速;a为紊流场衰减系数;vD，vW，vO为互不相关的零均值高斯白噪声，方差分别为QD，QW，RO。a 和QW由采样步长h、紊流尺度L 和紊流强度σ 决定

3.2 模拟数据处理

在模拟风场中，加入服从高斯分布的量测噪声，设置滤波各参数初值如下

由于风是一种大范围分布的空气运动，受周围环境和测量仪器的影响导致数据中掺杂野值，因此，仿真中在多处加入孤立野值和连续野值。分别使用Kalman 滤波算法和本文提出的抗野值强跟踪Kalman 滤波算法进行滤波处理，图2 是不同滤波算法的风速估计比较图。

图2 仿真模型风速估计对比图Fig 2 Comparison of wind speed estimation in simulation model

由图2 可以看出:Kalman 滤波具有一定的风场跟踪能力，但并未取得理想的滤波效果，受成片野值影响，结果出现大幅度跳变，滤波出现发散;而抗野值强跟踪Kalman 滤波在保证滤波精度的同时，能够有效抑制孤立野值或连续的影响，且精度较高，具有良好的鲁棒性。因此，抗野值强跟踪Kalman 滤波算法无论在滤波的精度还是收敛性方面均远优于Kalman 滤波，适合工程应用。

3.3 实测数据处理

以某型气象无人机2008 年4 月17 日飞行探测数据为例，将本文方法用于实测数据处理中，如图3 所示。图中可以看到无人机初期和末期处于爬升和下降阶段，受气流扰动较为严重，风速值出现一定幅度的波动，甚至出现野值，两种数据处理方法都具有一定的跟踪能力，但Kalman 规避连续野值的效果不佳，且滤波精度不高，而抗野值强跟踪Kalman 滤波成功处理了连续野值，表现出较好的抗野值能力。图4 是图3 的局部放大图。由图4(a)可知，抗野值强跟踪Kalman 滤波算法较Kalman 滤波算法具有更好的风场跟踪能力;由图4(b)可知，抗野值强跟踪Kalman 滤波算法具有更优秀的抗野值能力。

图3 风速估计对比图Fig 3 Comparison of wind speed estimation

图4 风速估计局部对比图Fig 4 Local comparison of wind speed estimation

4 结 论

滤波的精度和稳定性是无人机测风数据处理的关键，常用的Kalman 滤波算法的跟踪能力和抗野值能力欠佳。因此，本文结合Sage-Husa 滤波算法、强跟踪滤波算法、抗野值修正算法的特点，根据实际新息和理论预计的判别关系，自适应选择滤波算法。最后利用仿真和实测风场数据证明了该方法不仅克服了孤立野值和成片野值对滤波带来的不利影响，同时也保证了滤波精度，具有较强的鲁棒性，可作为无人机测风系统有效的数据处理方法。

［1］ 张晓芳，严 卫.中高层大气探测技术的研究进展［J］.气象科学，2007，27(4):457－463.

［2］ Kang H，Yang Q，Butler C，et al.Optimization of sensor locations for measurement of flue gas flow in industrial ducts and stacks using neural networks［J］.IEEE Transactions on Instrumentation and Measurement，2000，49(2):228－233.

［3］ 胡 锋，孙国基.Kalman 滤波的抗野值修正［J］.自动化学报，1999，25(5):692－696.

［4］ Efe M，Bather J A，Atherton D P.An adaptive Kalman filter with sequential rescaling of process noise［C］∥American Control Conference，1999:3913－3917.

［5］ Ristic B，Arulampalam M S.Tracking a manoeuvring target using angle-only measurements algorithms and performance［J］.Signal Processing，2003，83:1223－1238.

［6］ 柯 晶，钱积新.基于逻辑转换的改进强跟踪卡尔曼滤波器［J］.电子学报，2002，30(6):925－927.

［7］ 高 宁，周跃庆，杨 晔，等.抗野值自适应卡尔曼滤波方法的研究［J］.中国惯性技术学报，2003，11(3):25－28.

［8］ 肖亚伦，金长江.大气扰动中的飞行原理［M］.北京:国防工业出版社，1993.

［9］ 蔡 崧，产竹旺.基于自适应滤波的风场测量仿真试验平台［J］.计算机工程，2003，29(18):192－194.

［10］陆宇平，胡亚海.基于空间相关函数的二维紊流场数值生成法［J］.南京航空航天大学学报，1999，31(2):139－145.