大视场星敏感器标定技术*

李勉洪，丁国鹏，郑伟波

(中国科学院 上海技术物理研究所，上海200083)

0 引 言

星敏感器是以恒星为参照物的高精度空间姿态测量装置，它通过探测识别天球坐标系中恒星来确定卫星、导弹等航空航天飞行器相对于惯性坐标系的三轴姿态，具有重要的应用价值。目前，星敏感器正沿着高可靠性、小型一体化、自主、大视场、高数据更新率、高精度的方向发展［1］。单星测角精度是星敏感器整体精度的基础，它直接影响姿态角测量精度。大视场光学系统会引入的非线性畸变，随着星敏感器的视场角增大，将会影响其测量精度。另外，加工装配误差使得探测器平面存在倾斜旋转，这将导致图像出现倾斜畸变，从而影响星敏感器的测量精度。因此，必须对于大视场星敏感器进行标定，实现畸变校正，以便提高星敏感器整体测量精度。

目前，通常采用畸变模型法［2］及其改进方法，比如:分区线性畸变模型校正［3］实现畸变校正，或者通过直接映射法［4］进行畸变校正。但是大视场光学系统的畸变无法准确进行数学建模，精度要求越高，模型越复杂，参数越多，位置变换关系越复杂，不适合实时计算。而随着视场角和探测器分辨率的增大，直接映射法需要建立庞大的位置映射表，而采用细分法进行亚像元质心定位后，其映射表将变得更大，不适用于嵌入式系统。对此，本文提出一种基于遗传算法优化的BP 神经网络算法进行大视场星敏感器的标定方法，利用BP 神经网络的泛化能力表达复杂的非线性畸变模型，再通过遗传算法优化克服BP 神经网络局部优化的缺陷。

1 星敏感器标定原理

1.1 单星成像模型

空间物体到相机成像平面的成像过程通常可以看作是一个中心投影的过程，一般使用针孔成像模型来描述，如图1所示。图中Oc为投影中心，在摄像机模型中称为光心，其到成像平面π 的距离f 称为焦距。过点Oc垂直成像平面π 的直线称为主轴，其与成像平面的交点Os称为主点。空间恒星Pc与光心Oc的连线与成像平面的交点Ps即为该恒星在成像平面所成的像。

图1 星敏感器成像原理图Fig 1 Imaging principle of star sensor

根据上述投影模型建立摄像机坐标系OcXcYcZc，成像平面坐标系OsXsYs以及计算机图像坐标系OiXiYi，假设恒星P 在该坐标系下的单位向量为Pc=［X，Y，Z］，其在成像平面所成的像在图像坐标系下通过质心定位获得的坐标记为Pi=［u，v］，单位为像素(pixel)，主点Os在图像坐标系的坐标记为Po=［u0，v0］，则可以建立如下投影关系的数学描述

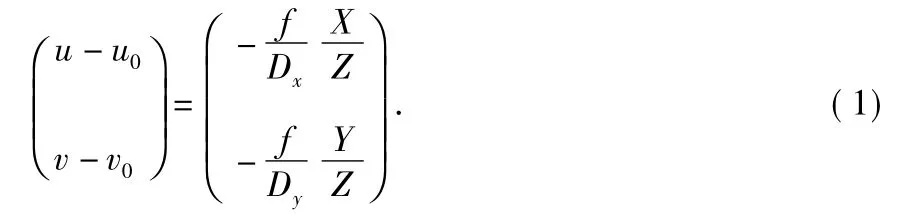
其中，Dx，Dy分别为探测器像元的高和宽。

1.2 单星测角原理

图2 所示为单星测角系统。

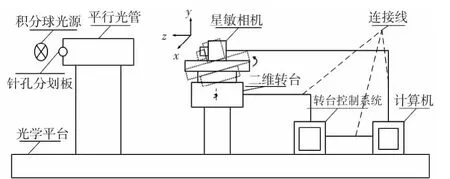
图2 单星测角系统Fig 2 Single star angle measurement system

该系统在测量过程中使用了高精度的二维转台(精度为0.001°)，把大视场星敏相机固定在二维转台上，积分球光源通过针孔分划板的光被平行光管准直后形成的平行星光在相机成像平面的主点位置产生星点像。转动二维转台，记下此时二维转台的旋转角度值为［ωx，ωy］，则由坐标系旋转矩阵可以获得平行光管产生的星点目标在摄像机坐标系的单位向量为

由式(1)和式(2)可以获得星点像坐标与转台角位置的关系

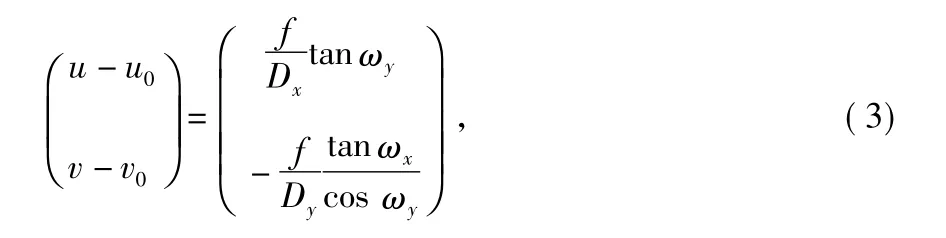
则根据星点像质心位置，可以反推得出二维转台的角位置

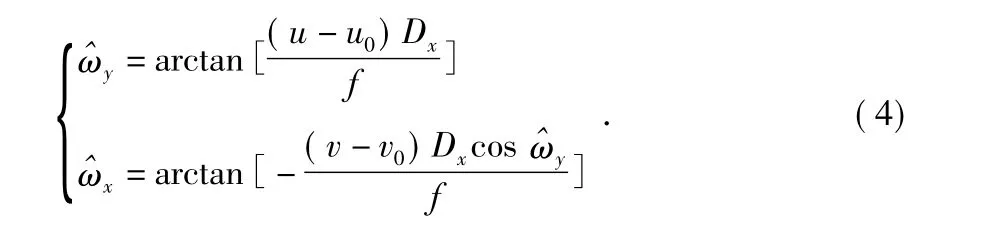
1.3 标定原理

星敏感器光学系统存在不同程度的几何畸变，视场越大，畸变程度越严重。另外由于存在加工误差和装配误差，探测器成像平面与光学系统的光轴并不严格垂直，探测器成像平面与理想安装方式有一个旋转角度，成像平面主点位置发生偏移，这些因素都将导致实际星像点的质心位置P'i=［u'，v'］与理想星像点质心位置Pi=［u，v］并不重合，从而引入测角误差，影响星敏感器精度。

星敏感器的标定原理是通过一些已知的参考点，即无失真图像中某些星像点质心位置和畸变图像相应星像点质心位置间对应关系，建立起整个图像中畸变坐标与理想坐标之间的映射关系，从而达到标定的目的。

鉴于星敏感器畸变模型无法准确建模以及直接映射法在大视场和大分辨率图像的应用场景下数据量庞大的缺陷，本文采用BP 神经网络来表达星敏感器畸变这一非线性系统，并通过遗传算法优化BP 神经网络，从而实现大视场星敏感器的标定。

2 标定方法与关键算法

2.1 BP 神经网络模型

BP 神经网络是一种多层前馈神经网络，其网络拓扑结构如图3 所示。其中，ai，bk为神经网络阈值，wij，wik为神经网络权值。从图3 可以看出:BP 神经网络可以看成一个非线性函数，神经网络权值和阈值为该函数的参数。输入信号从输入层经隐含层逐层处理直至输出层，如果输出层得不到期望输出，则反向传播，根据误差调整网络的权值和阈值，从而使BP 神经网络不断逼近期望输出。

图3 BP 神经网络拓扑图Fig 3 Topological diagram of BP neural network

2.2 获取神经网络训练样本集

假设星敏相机的视场角为θx×θy，其中，θx为水平视场角，θy为垂直视场角;图像尺寸为M×N，焦距为f，采用图2所示的测角系统，将星敏相机固定于二维转台上，保证相机光轴于平行光管光轴，采集图像并获得星像点的位置坐标为C00=［x00，y00］，分别以Δθx和Δθy的角度增量在相机视场范围内旋转二维转台X 方向和Y 方向，则可以得到二维转台在视场范围内的角位置为

在上述二维转台的每个角位置获取图像并通过文献［5］所述质心定位算法获得对应星像点sij的坐标位置

其中，xij和yij分别为图像平面的行坐标和列坐标。

根据以下公式

构造畸变样本集合

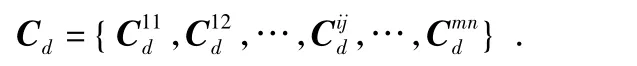
根据公式(3)可以获得星像点Sij对应的理想成像坐标记为由此构造期望输出理想样本集Cu=。根据式(8)采用最大最小法归一化Cd，Cu得到归一化的输入样本集和对应的输出样本集

其中

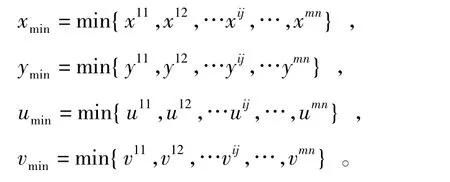
2.3 遗传算法优化BP 神经网络算法

BP 神经网络是以梯度下降法为基础的非线性优化方法，不可避免存在局部极小问题。而且实际问题的求解空间往往是极其复杂的多维曲面，存在许多局部极小点，更使网络陷入局部极小点的可能性增加，采用随机初始化神经网络的权值和阈值的方法很难使得网络训练达到全局最优［6］。本文采用遗传算法对BP 神经网络进行优化，通过遗传算法得到更好的网络初始权值和阈值，其基本思想就是利用个体代表网络的初始权值和阈值，通过遗传操作寻找最优个体作为BP 神经网络的最优初始权值和阈值。具体操作步骤如下:

1)确定神经网络拓扑结构，采用三层BP 神经网络，输入层节点数p=2，输出层节点数q=2，隐含层节点数l ＜，其中，a 为0～10 之间的常数，输入层和隐含层的节点转移函数采用log－sigmoid 函数，输出层节点转移函数采用线性函数。

2)通过遗传算法优化BP 神经网络的初始权值和阈值。遗传算法的基本要素包括染色体编码方法、适应度函数、选择、交叉和变异等遗传操作以及运行参数。

本文采用实数串编码方式，每个个体均用一个实数串表示，由输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值和输出层阈值4 部分组成，第i 个个体ai表示为{ai1，ai2，…，ain}其中，n=(p+q+1)×l+q，i=1，2，…，N，N 为种群规模。

采用神经网络预测误差大于某个阈值的比例作为个体的适应度值，即将每个个体作为BP 神经网络初始权值和阈值，用训练样本集进行初步训练，得到的预测误差大于某个阈值的比例作为个体适应度，个体适应度越小，个体越优。

采用实数交叉，第k 个染色体ak和第l 个染色体al在j 位的交叉操作方法如下

其中，b 为0 ～1 之间的随机数。

变异操作，选取第i 个个体的第j 个基因aij进行变异，变异操作如下

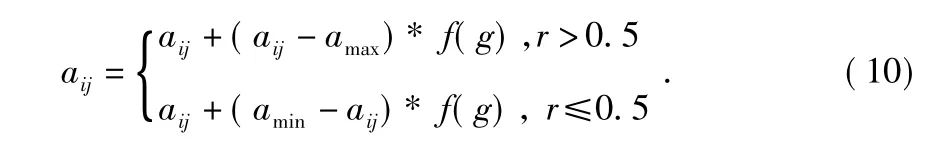
其中，amax为基因aij的上界，amin为基因aij的下界，f(g)=r2(1－g/Gmax)2，r2为一个随机数，g 为当前迭代次数，Gmax为最大进化次数，r 为0 ～1 之间的随机数。

遗传算法优化的具体步骤如下:

a.设置种群规模、进化次数、交叉概率以及变异概率;并在初始化范围内初始化每个个体，并计算每个个体的适应度;

b.进行选择、交叉和变异操作获得新一代种群，计算该种群每个个体的适应度，从中找出最优个体并替换最差个体;

c.判断是否达到终止条件，即进化次数是否结束，若不是，则返回上一步;

d.将最优个体的实数编码保存下来，作为下步神经网络训练的初始权值和阈值。

3)训练BP 神经网络，设置最大训练次数，学习速率和最大误差平方和，在每一轮迭代中，分别取训练样本集中畸变坐标样本作为神经网络输入，计算神经网络输出向量Oij，并与对应的理想输出样本比较。将比较误差用于调节神经网络连接权值和阈值，反复训练神经网络，直到满足终止条件，即到达迭代次数或者误差满足要求，保存该神经网络的结构和模型参数。

4)获得不同隐含层节点数下的神经网络结构及其模型参数，比较误差，保存最优的神经网络和模型参数作为最终畸变校正的模型。

3 实验与结果

实验用星敏感器的具体参数如表1 所示。

表1 星敏感器参数Tab 1 Parameters of star sensor

根据2.1 小节所述采集获得神经网络训练样本集，其中Δθx=Δθy=1°，共获得个4 870 个有效样本。其对比图如图4 所示。

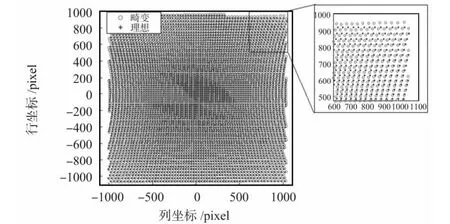
图4 畸变坐标和理想坐标对比图Fig 4 Comparison of distorted coordinates and ideal coordinates

根据上述训练样本训练遗传算法优化的BP 神经网络，设置BP 神经网络最大训练次数为800，学习速率η=0.01，允许最大误差平方和为ε=0.001，设置遗传算法种群规模为15，进化次数为50，交叉概率为0.3，变异概率为0.2，训练得出神经网络结构参数，进行坐标畸变校正。可以得到校正坐标和理想坐标的对比图如图5 所示。

图5 校正坐标与理想坐标对比图Fig 5 Comparison of calibrated coordinates and ideal coordinates

在与训练样本集不同的转台角位置获取测试样本集进行校正，并与文献［7］中所述的分区拟合方法进行比较，计算后误差分析如表2 所示。

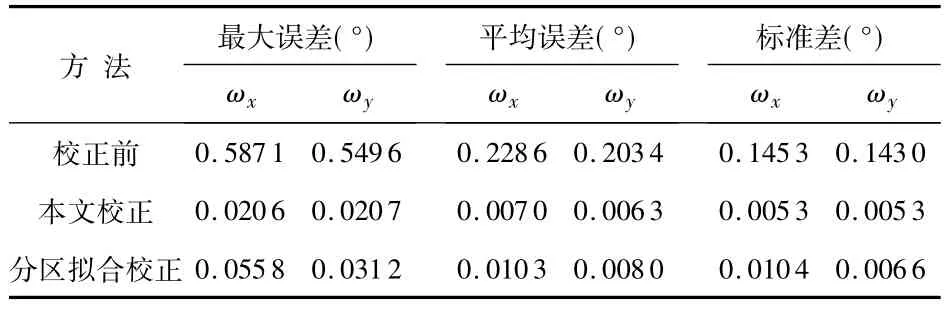
表2 误差分析Tab 2 Error analysis

假设分区整体拟合法将整个视场分为M×N 个区域，则拟合所得的参数个数为6×M×N，另外还需要M+N 个辅助参数，则总共有M+N+6MN 个参数，本实验采用M=N=3 的分区参数，则总共有60 个参数。而本文方法需要5l+2 个神经网络模型参数，其中，l 为隐含层节点数，取值范围为2 ～12，另外需要10 个辅助参数，本实验中l=9，因此，总共需要57 个参数。

而由表2 可以得出，遗传算法优化BP 神经网络算法的平均绝对误差和最大绝对误差相比分区整体拟合法均有所降低，在所需参数相近的情况下，精度比分区整体拟合法提高将近1 倍，这说明本文提出的大视场星敏畸变校正方法是一种有效的方法。

4 结 论

本文分析了影响星敏感器测角精度的因素，建立了大视场星敏感器标定系统，提出使用BP 神经网络表达大视场星敏感器畸变这一非线性模型，并采用遗传算法优化BP神经网络，克服其容易陷入局部优化的缺陷。实验结果表明:本文提出的标定方法精度高，使得单星测角误差由标定前的0.14°降低到0.0053°，测角精度提高将近30 倍，并且效率高，稳定性好。

［1］ 孙高飞，张国玉，郑 茹，等.星敏感器标定方法的研究现状与发展趋势［J］.长春理工大学学报:自然科学版，2010，33(4):8－14.

［2］ 杨比武，郭晓松.摄像机镜头非线性畸变校正方法综述［J］.中国图像图形学报，2005，10(3):269－274.

［3］ 刘力双，孙双花，吕乃光，等.一种图像测量系统的现场标定和畸变校正方法［J］.传感器与微系统，2008，27(5):66－68.

［4］ 邓 雷，龚惠兴.一种实用广角成像系统几何畸变数字实时校正方法［J］.红外技术，2006，28(10):571－575.

［5］ 李玉峰，郝志航.星点图像超精度亚像元细分定位算法的研究［J］.光学技术，2005，31(5):666－668.

［6］ 秦庆兵.基于神经网络的摄像机畸变校正研究［D］.沈阳: 东北大学，2010.

［7］ 乔培玉，何 昕，魏仲慧，等.高精度星敏感器的标定［J］.红外与激光工程，2012，41(10):2779－2784.