泥浆脉冲发生器转子水力转矩多相流数值模拟

，， ，

(1.浙江大学 海洋学院，浙江 杭州 310058；2.华中科技大学 船舶与海洋工程学院，湖北 武汉 430074；3.中船重工第715研究所，浙江 杭州 310023)

0 引言

泥浆脉冲发生器是随钻测量、随钻测井系统中重要的组成部分[1]。脉冲发生器中转子的水动力学特性直接影响到脉冲发生器的性能。

程烨对工作流体为纯水时往复式脉冲发生器水力转矩做过详尽的分析[1]，并提出了对脉冲发生器的修改意见[3]。王智明等就高速泥浆脉冲发生器进行过设计研究[4]，以及探讨在不同环境参数下，定转子形状对水动力矩的影响[5-6]。高勇海就深水油气钻探的多相流动进行相关研究，得到了井筒任意一时刻的温度、压力场、各相体积分数等物理[7]。韩洪升等通过实验对油井内多相流动的压力分布进行了相关研究，该方法误差较小[8]。白博峰等从宽广的实验参数出发，对多相流的压力和压差信号进行分析和流型在线识别进行研究[9]。目前，从多相流角度对往复式脉冲发生器的水动力学特性进行研究比较缺乏。

本文利用CFD数值仿真技术对各种情况下的脉冲发生器的内部流场进行仿真分析，着重分析多相流因素对转子水动力矩的影响和流体介质中固相物质的分布特性。

1 数学模型

流体的运动受到相关物理守恒定律的支配，这些基本守恒定律包括：质量守恒定律、动量守恒定律和能量守恒定律。当流域系统处于湍流状态时，系统必须同时遵守湍流输运方程。本研究中，忽略温度变化的影响，即不引入能量方程。

(1)连续性方程

(1)

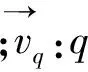
(2)流体相q的动量方程

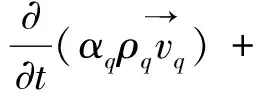
(2)

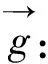
(3)固体相s的动量方程

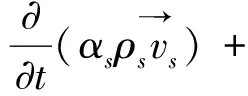
(3)

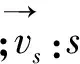
本研究中，流体通过转子会形成复杂运动形式，是湍流状态。这里介绍不可压缩流体的标准方程：

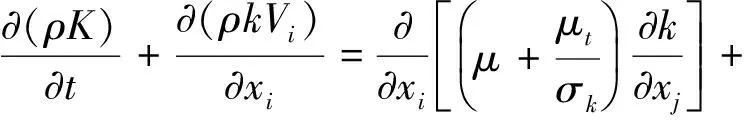
←GK+Gb-ρε-YM

(4)

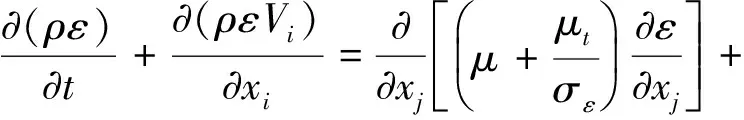
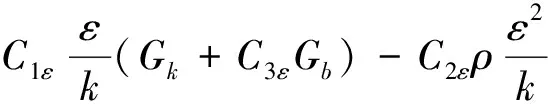
(5)

其中，ρ：流体密度；Vi：速度的指标计法，i向速度；μ：流体动力粘度；Gk：由平均速度梯度导致人湍动能生成项；Gb：由浮力引起的湍动能生成项；C1ε、C2ε、C3ε为经验常数，FLUENT中的默认值为：C1ε=1.44、C2ε=1.92、C3ε=0.09；σk、σε分别为湍动能和湍动耗散率对应的普朗特数，FLUENT中的默认值为：σk=1.0、σε=1.3；YM：可压缩湍流脉动膨胀对总的耗散率的影响；ε：耗散率；μt：湍动粘度；k：湍动能；xi、xj坐标的指标记法。

本研究中采用标准模型求解该流动问题，控制方程由1、2、3、4、5组成，采用有限体积法对控制方程进行求解。

2 数值分析

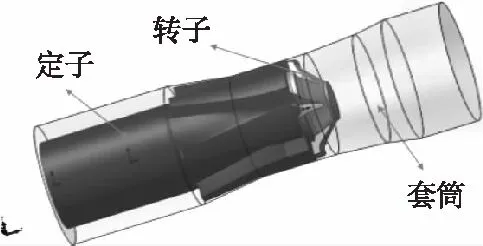
图1 脉冲发生器三维模型图

本文研究中的脉冲发生器结构复杂，特别是有许多细小构件。在保证计算精度前提下，将研究对象简化为套筒、定子和转子的组合，并对脉冲发生器内部流场做出一定简化处理。简化后脉冲发生器三维模型如图1所示。

用Gambit软件对建立好的模型进行网格划分，使用非结构网格划分方法，采用动网格技术实现网格更新，转子运动方程由UDF(User-defined function)嵌入到Fluent中。而后使用CFD计算软件对模型进行不同条件下的流场特性仿真分析。本文中通过控制转子的匀速运动或静止在不同位置仿真流场，以得到稳态水力转矩。流场仿真的过程中，考虑固、液二相流的影响，采用求解精度较高的Euler模型，二相流入流速度10.5 m/s，水相和固相的速度均为10.5 m/s，固相细砂的体积分数为1%，细砂质量中位径0.000 5 m，出口压力0.65 MPa，采用四面体网格划分，网格数为2.58×106，计算步长2×10-5，计算10 000步，定转子间隙为1.5 mm，转子旋转速度为2rad/s。

图2和图3分别是转子迎流和背流面水相体积分数分布云图。在定、转子相互衔接处，水相体积分数明显降低，细砂相体积分数达到最高。某些特定区域内细砂体积分数高达34.2%，远大于总体多的1%的细砂体积分数含量。可以推断在脉冲发生器中，定转子相衔接处会大量聚集固相物质。

3 多相流因素影响分析

3.1 多相流因素的影响分析

当流体工作介质为固、液二相流时，转子水动力转矩会受到细砂的影响，同时也需考虑水和细砂间的相互作用，这与工作介质是纯水时是不同的。这里以定转子间隙1.5 mm、细砂体积分数1%，转子转速2 rad/s,入流速度10.5 m/s的情形，分别研究流体工作介质为纯水和固、液二相流时的情况，进行数值仿真。

转子转动角度对于水力转矩的影响十分明显。随着转动角度增大，转子水力转矩随之增大，并在接近20°时，转子水力转矩达到最大值，这个地方即定转子接近闭合处。最大水力转矩为8.018 4 N·m。水动力转矩达到最大值后随着转子的继续转动，转子水动力转矩减小。值得注意的是转子转动之初，定转子并无相对转动角度，但是存在一个很小的转动力矩0.993 N·m。

转动角度在0到5°时，基于二相流的模拟结果和纯水的结果差别极小；而当转动角度在5°到10°时，转子水动力矩小于纯水时的值；到转动角度增大至15°至20° 时，二相流时的水动力矩明显大于纯水时的结果，之后纯水时的水动力矩基本大于二相流时的情况。总体而言，二相流结果和纯水结果有一定差别，但总体上讲两者差距不大。

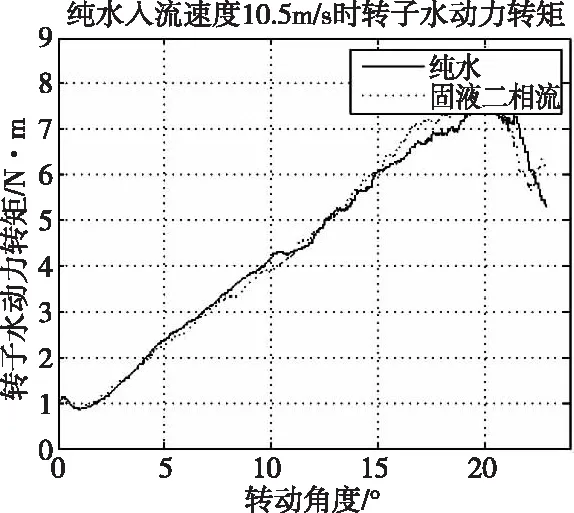
图4 不同流体工作介质下水动力转矩与转动关系图

由图4可知，固、液二相流因素对转子水动力转矩的影响较小。程烨[2]在其论文中所得出结论是流体工作介质为在纯水中时进行研究得出的。所以，这也部分证明程烨在其论文中得出的结论具有一定的适用性。

当然，固、液二相流对转子水力转矩存在一定的影响，特别是在定转子闭合处附近，固、液二相流的影响相较而言比较明显，此处固、液二相流使转子水力转矩偏大。经过计算，可知这种转子水力转矩的差距不仅仅是由二相流相对于纯水的流体密度变化所引起的。故而，可以推断：固相物质细砂对转子存在一定的作用，流体工作介质中液相和固相存在的相互作用，这种相互作用影响到转子的水力转矩。但更重要的是，定转子闭合附近，固相物质细砂在转子附近大量聚集导致转子水力转矩相对于纯水时有比较明显的变化。

对转子迎流面进行如下研究。

如图5和6所示为在不同流体工作介质条件下转子迎流面的压强云图。可以看出，转子表面压强分布基本一致，即多相流的因素并未改变压强的分布规律。但由于细砂相的作用，固、液二相流为流体工作介质时，压强数值相对于纯水时偏大,同时在转子表面会出现局部压强偏高的情况，与纯水是压强平缓过度不同，可以推断细砂在转子表面的聚集影响到转子表面的局部压强的分布。

速度矢量分布规律大体一致，多相流因素并未改变速度梯度分布的规律。但与此同时也可观察出，以固、液二相流为流体工作介质的条件下，转子表面处速度值偏大。比如，流体工作介质为纯水时水的最大速度值为84.5 m/s，流体工作介质为固、液二相流时水相的最大速度值可以达到104 m/s。

3.2 入流速度的影响分析

本文研究过程中，通过往复式脉冲发生器的流量分为2 500 L/min、2 000 L/min和1 500 L/min三种情况。因此在研究中，将选用6.3 m/s、8.4 m/s和10.5 m/s三种入流速度进行研究。其他的变量为：定转子间隙为1.5 mm、细砂体积分数含量为1%和转子旋转速度为2 rad/s。

由图9可知，往复式脉冲发生器实际工作时，在各入流速度下多相流因素对转子水力转矩存在一定影响，相对于纯水，二相流时的转子水动力矩和纯水时水力转矩相差在7.7%以内。这是由于细砂相与水相的相互作用和细砂相对转子的作用导致的。同时，转子水力转矩直接与入流速度成正相关的关系。

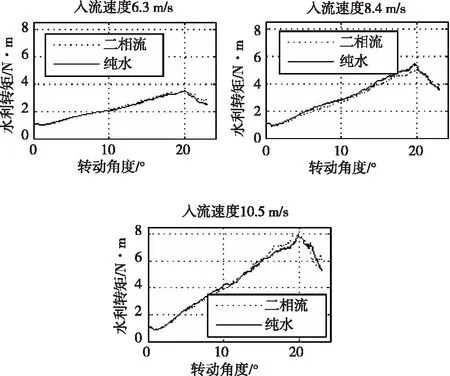
图9 不同流体工作介质各入流速度时转子水动力转矩

大致看来，转子水动力转矩与速度的平方成正比关系，即与通过脉冲发生器的流量成正相关关系。与此同时，当其他变量一致时，转子水力转矩并非严格与速度的平方成正比的关系。这一点可以从表1中转子的最大水力转矩值与速度的平方的商的数据中明确观察到。所以，可以推断随着速度的增大，流体工作介质中水相与固相的相互作用和固相对转子的作用会愈加明显。

固、液二相流中的水相和细砂相的速度在转子附近处达到最大值。水相和细砂相的速度严格与入流速度正相关。其中水相速度最大值大概与入流速度有着接近10倍的关系。

选取转子迎流面为研究对象，转子迎流面水相的体积分数分布云图如图10、11、12。

转子附近二相流中细砂的体积分数改变剧烈，入流速度为6.3 m/s、8.4 m/s和10.5 m/s时，细砂相最高体积分数为0.386、0.368和0.370。如图11、图12、图13表现的细砂体积分数的分布规律可知，二相流中各相的分布与入流速度的大小无关。

3.3 旋转速度的影响分析

将流体工作介质改变为固、液二相流，细砂体积分数1%，其他条件不变。转速为零时的计算结果如表2呈现。选取旋转速度为1 rad/s、2 rad/s和转子静止时的三种情况进行数值计算。

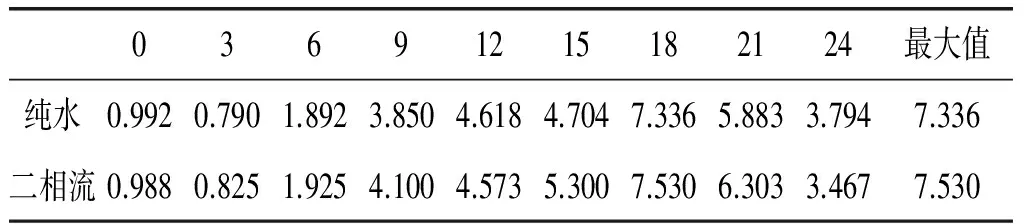
表2 转子静止时二相流和纯水时各相对转动角度下水力转矩值

将计算结果与流体工作介质为固液二相流时进行对比，有图13。

图13 不同流体工作介质时各旋转速度下转子水力转矩与转动角度关系图

由图13可知，在各旋转速度下，固、液二相流相对于纯水而言，对转子水力转矩的影响不大。在只是宏观上考虑转子水力转矩时，可以忽略二相流的影响。

3.4 定转子间隙的影响分析

定转子间距对水动力特性的影响十分重要。在实际钻井过程中，由于不同井深对于信号发生强度的要求不同，这里主要通过定转子间隙实现。本节采用细砂体积分数为1%、入流速度为10.5 m/s、转子转速为2 rad/s的基本条件，分析定转子间距为1 mm、1.5 mm和2 mm三种情况下流体介质为固、液二相流和纯水时的转子水动力转矩。

如图14所示，再次证明一般情况下多相流因素对转子转动力矩影响较小。定转子为1 mm时，流体介质纯水和二相流时，定、转子闭合处附近转子水力转矩的差异正好说明二相流因素在一定时候对转子转矩存在比较大的影响。

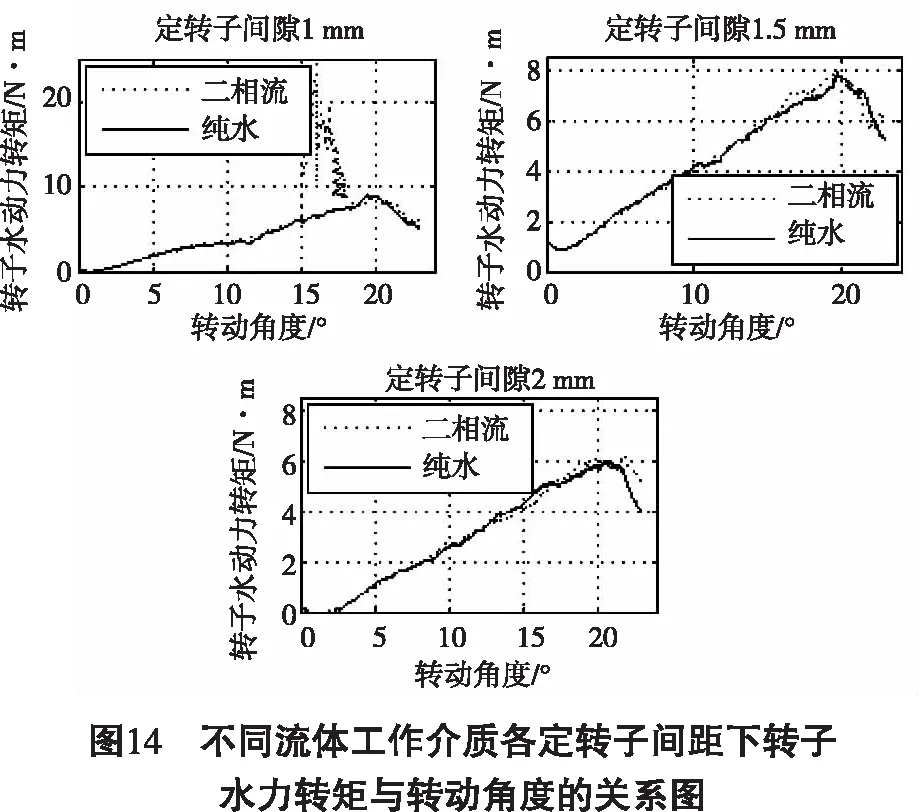
由表3中转子处水和细砂的最大速度值可以看出，随着转子定转子间距的增大，速度将降低，转子处压强降低，这也证明了，定转子间隙增大，转子处流动剧烈程度会降低，流动趋于平缓，水和细砂速度降低。

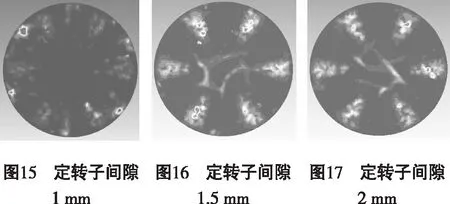
在定、转子之间截取平行于转子的平面，通过Fluent后处理功能观察此面上流体中相的分布情况。这里以水相为标准研究。

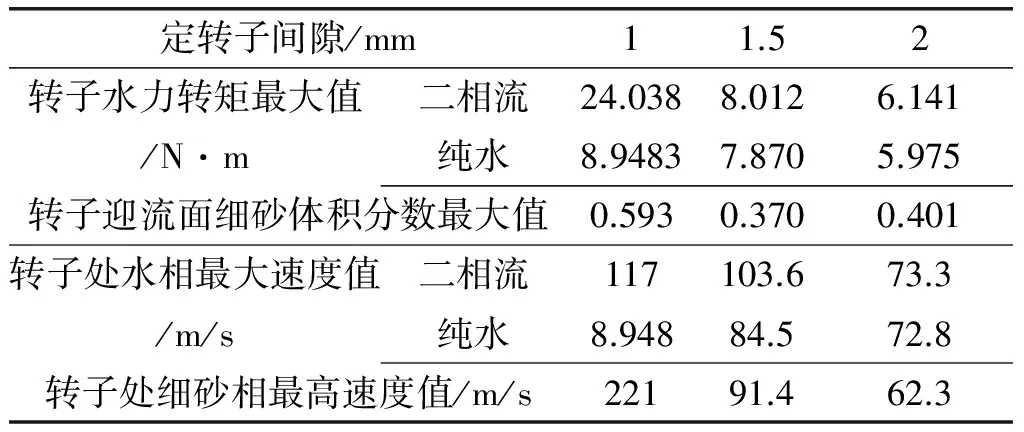
表3 不同定转子间隙下转子水力转矩

如表3所示，转子为1 mm时，定、转子间隙之间的细砂相体积分数最大。综合比较三种情况下水相的分布图和表3所示细砂相体积分数最大值，可以知道二相流中定转子处相的分布与定转子间隙存在一定的关系。

3.5 细砂体积分数的影响分析

在实际工作过程中，所使用的钻井液各种各样，固相的体积分数含量也各不相同。同时，当选定某种钻井液之后，在实际钻探过程中，由于流动的复杂性，在整个流道中钻井液并非绝对均匀混合。因此，有必要针对不同的固相体积分数这个变量进行研究，以探索不同固相物质体积分数对转子水动力力学性能的影响。本小节中采用定转子间隙为1.5 mm、入流速度为10.5 m/s、转子以2 rad/s的速度匀速旋转的基本条件，研究细砂体积分数分为0.2%、0.6%和1%三种情况。同时以纯水时的情况作为对比。

图18 不同固相体积分数时转子水动力与转动角度的关系

根据图18可知，流体工作介质中细砂的体积分数对于转子宏观上的水力力矩的影响不大。在研究转子整体的水力转矩，而不考虑局部受力的情况下。是可以忽略流体工作介质中固相物质的影响。

根据表4可知，随着细砂体积分数的增加，转子最大水力转矩有微小的增加。表明：二相流中固相物质对转子水力转矩能起到一定的作用,但这种作用并不明显。

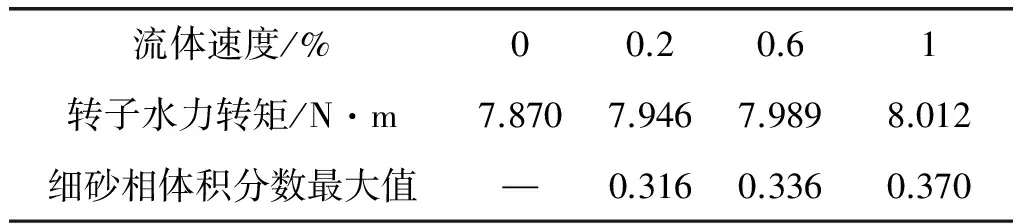
表4 不同细砂含量下最大转子水力转矩

由图19、图20和图21可知，随着二相流中细砂体积分数的增加，转子表面处产生的固相物质的集聚的现象愈发明显。从中也可以看出，细砂虽然在转子表面聚集，但在转子表面也并非均匀分布，而是在叶片的迎流处再次集聚，导致局部的细砂体积分数异常的高于平均值。这一点在表3中细砂相体积分数最大值中也有明显的体现。

4 结论

1)定转子衔接区域体现出固相物质聚集的特性，某些情况下个别区域固相物质体积分数可达50%，因此转子叶片将受到固相物质复杂的作用力；

2)相较与流体工作介质为纯水的情况，多相流因素对往复式脉冲发生器中转子的水力转矩有一定的影响，但总体而言影响较小；

3)定转子区域固相物质聚集情况与流体入流速度相关性较小，与定转子间隙和固相物质体积分数的相关性较大，即定转子间隙和流体工作介质中固相物质体积分数会对定转子间隙处固相物质的分布影响较大。

[1] Chin W C.MWD siren pulser fluid mechanics[J].Petrophsics,2004,45(4)363-370

[2] 程烨.往复式脉冲器转子水力特性研究[D].浙江大学硕士学位论文，2014

[3] 程烨，王智明，陆庆超，瞿逢重，王赤忠.往复式泥浆脉冲发生器转子水力转矩[J].石油学报，2014,35(2)385-389

[4] 王智明，菅志军，李相方，等.连续波高速率泥浆脉冲器设计研究[J]. 石油天然气学报，2008, 30(2)611-613

[5] 王智明，肖俊远，管志军.旋转阀泥浆脉冲器转子水力特性研究[J].石油矿场机械，2012,41(3)：1-3

[6] 王智明，肖俊远，管志军.基于CFD的旋转阀泥浆脉冲发生器转子结构参数研究[J].现代制造技术与装备，2011(6)3-4，26

[7] 高永海.深水油气钻探井筒多相流动与井控的研究[D].中国石油大学博士学位论文.2007

[8] 韩洪升，陈家琅.油井内多相流动压力分布的计算方法[J].大庆石油地质与开发，1990.6.Vol9(2)49-59

[9] 白博峰，郭烈锦，王忠勇，张西民.油气水多相流压力和压差信号特征分析和流型在线识别[J].工程热物理学报，2002.5.Vol23(3)357-360

[10] 车得福，李会雄.多相流及其应用[M].西安：西安交通大学出版社，2007:66