混合磁化永磁联轴器的优化设计

， ，

(合肥工业大学 机械与汽车工程学院，安徽 合肥 230009)

0 引言

近年来，许多国外研究学者对磁力联轴器永磁体的充磁方向进行了研究，并提出了方形、平行结构之间的磁力解析计算方法，Yonnet[1]，Fuvaev[2], Lemarquand[3]提出的基于磁极理论两块立方、平行永磁体之间的力矩计算公式是极其重要的一种，这对永磁联轴器传动转矩的计算提供了一种新的方法。在实际工程应用中，公式计算存在很大的局限性，计算结果误差较大。通过Maxwell对这种联轴器进行计算，分析其传动特性，可直接获得最优的传动结构参数。

1 径向、切向磁化磁联轴器的结构原理

径向、切向充磁永磁联轴器的结构是一种将径向磁化的永磁联轴器和切向磁化的永磁联轴器充磁方式的一种混合设计。图1(a)、(b)分别为径向、切向磁化的永磁联轴器。根据这两种磁化方向，可以将两种磁化方式结合，得到径向、切向磁化永磁联轴器[4]。这种径向、切向磁化的混合型结构最大的优点就是：当径向磁化磁体体积等于切向磁化磁体体积时，具有最大传动扭矩，几乎是单一磁化型的2倍[5]，下面的所有分析模型中，径向磁化和切向磁化永磁体体积均相等。

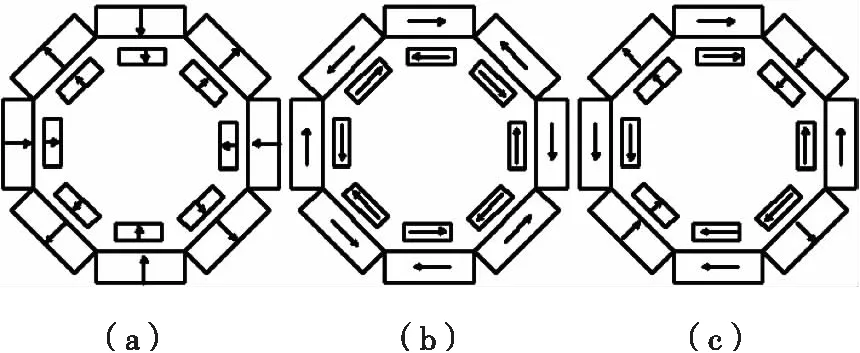
图1 磁力联轴器结构原理图

2 径向、切向磁化永磁联轴器模型

根据该联轴器的结构原理，利用Maxwell建立分析计算的三维模型。在此，首先分析在相同的永磁体体积的条件下，三种不同的充磁方式传递转矩的优劣。在该模型中最大半径Rmax=45 mm固定(Rmax为紧密排列的外永磁体内表面内切圆半径)；最小半径Rmin=38 mm固定(Rmin为紧密排列的内永磁体内表面内切圆半径)；磁极对数m分别取8、12、16、20、24对；同时为了减小分析的误差，本联轴器永磁体长度取L=1 000 mm，在Maxwell ansoft中二维计算时，设定轴向长度为1 000 mm。切向充磁的永磁联轴器中不能有轭铁存在，否则所有的磁通将全部聚集在铁芯中，因此只分析全永磁体的理论模型，并不考虑其安装情况[5]。

表1 模型建立的参数

根据表1各建模参数，在Maxwell Ansoft 里建立模型，由于此联轴器在结构上是严格的中心对称体，因此只要对模型进行二维截面分析。

3 分析结果

3.1 径向、切向磁化永磁联轴器磁场分布

计算分析采用的磁力联轴器模型参数如下：磁极对数m=16；外永磁体宽度为24 mm，厚度为5 mm；内永磁体宽度为18 mm，厚度为5 mm。在Maxwell中建立模型，并完成了材料属性、网格划分、边界类型等一系列求解条件的设置，最后进行了分析。图2显示了分析的结果, 由本图可以直观地了解磁力联轴器处于最大传动转矩位置时的磁场分布和磁密大小；其中气隙的磁场强度基本在0.664 72T和1.1965T之间。

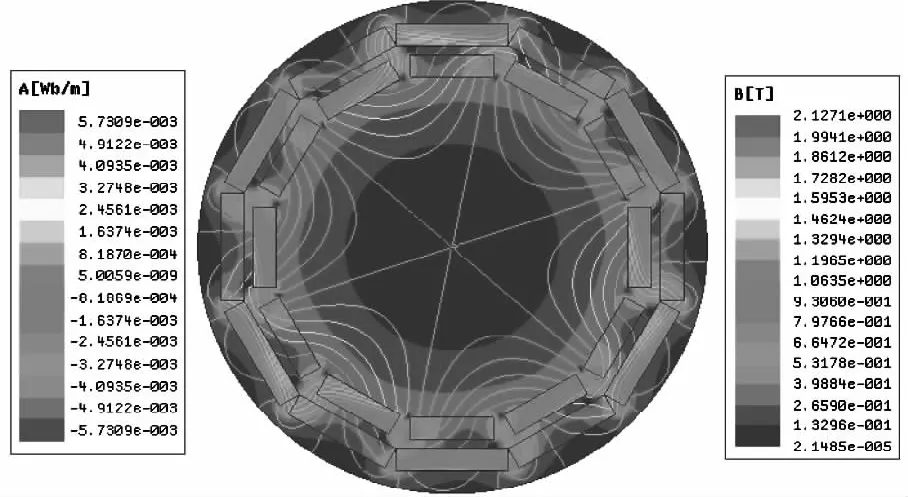
图2 径向、切向充磁计算模型

3.2 传动与角度的关系

径向、切向磁化的永磁联轴器属于同步磁力联轴器，正常工作时，其内、外转子处于相对静止的状态，并存在一个稳定的角度差；磁力联轴器的角度和传动转矩的关系决定了磁力联轴器的工作性能。本文对磁极对数m分别为8、12、16、20、24的磁力联轴器模型在其磁体分布的半个周期内进行计算，其对应的半周期分别为：90°、60°、45°、36°、30°，得到的扭矩关系如图3所示。

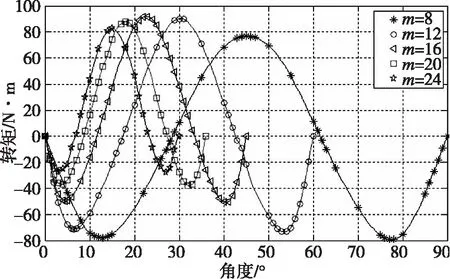
图3 传动转矩与角度差的关系

由图3可以得到如下结论：

1)磁力联轴器的最大转动转矩随着磁极对数的增加呈先增加后减小的趋势；其主要原因是当磁极对数较少时气隙磁密度没有达到饱和状态，因此传动转矩随着永磁体对数的增加而增加，当磁极对数增加到一定数目时，气隙磁密度达到饱和或过饱和，此时漏磁的增加速率快于磁密增加的速率，从而出现传动转矩下降的趋势[6]；最佳的磁极对数为12或16，可传递的最大转矩为90 N·m。

2)最大正向传动转矩基本都是在磁体分布周期的1/4处，即内、外转子角度差分别为45°、30°、22.5°、18°、15°时对应的传动转矩是磁联轴器的最大传动转矩。

3)最大反向传动转矩随着磁极对数的增加而呈下降的趋势，在磁极对数为8时，正负最大传动转矩几乎一样，但磁极对数增加至24时，最大负转矩比最大正转矩的一半还小，而且正向传动转矩的分布区域所占的比例也随着磁极对数的增加而增加。由于联轴器的工作区域越宽越有利于力矩的传动，联轴器工作也越稳定。因此，取正传动区域为联轴器理想工作区时，增加磁极对数可增宽联轴器的工作区域，从而提高联轴器工作的稳定性。

3.3 磁极厚度对传动转矩的影响

3.3.1 外永磁体厚度与转矩的关系

永磁体的厚度对磁力联轴器的最大传递力矩有着决定性作用，是磁力联轴器设计的重要参数。将五组模型的内永磁体固定为5 mm，内、外转子角度差设为各自的最大传动转矩处，即1/4周期，对各组外转子永磁体在不同厚度条件下进行计算得到图4所示结果。

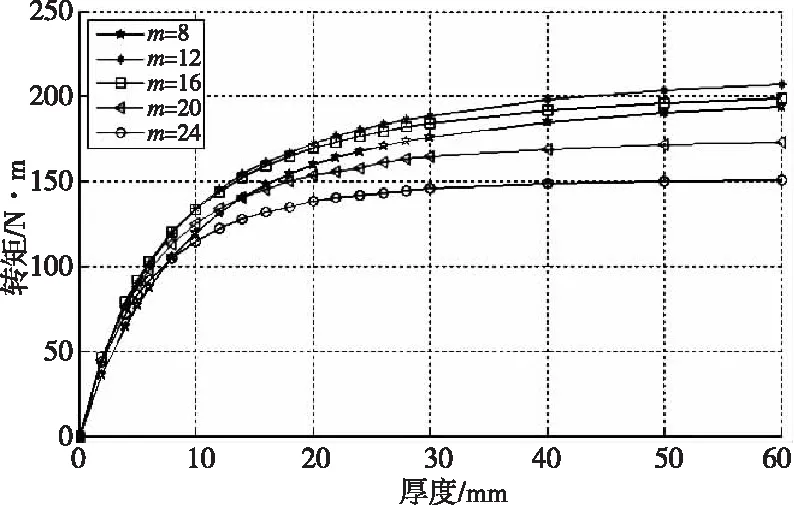
图4 外永磁体厚度对转矩的影响

由图4可知：当磁体厚度增加时，磁力联轴器的最大传动转矩也随着上升；当永磁体厚度增加到20 mm时，转矩增加的幅度快速减小，当永磁体厚度增加到40 mm以后，最大传动转矩基本不再上升。产生这一现象的主要原因是磁体厚度较小时，产生的气隙磁场密度较小。随着永磁体厚度不断增加，并达到一定值时，气隙磁场密度达到饱和，所增加的磁势与增加的磁阻和漏磁相当而抵消，气隙磁场密度趋于稳定。因此，在设计这种磁力联轴器时，应选取适中的磁体厚度；永磁体太薄，不能产生饱和的气隙磁场，传动能力较低；永磁体太厚，将造成不必要的浪费，还增大了联轴器整体结构。由计算结果可知，最佳的永磁体厚度为20 mm。

3.3.2 内永磁体厚度与转矩的关系

对于内永磁体的厚度而言，其长度和宽度是互相变化的，当外永磁体紧密排列且磁极对数确定时，外永磁体的宽度就是唯一的。因此，当内永磁体也与外永磁体同样紧密排列时，具有最大的传动效果，其参数关系如图5所示。

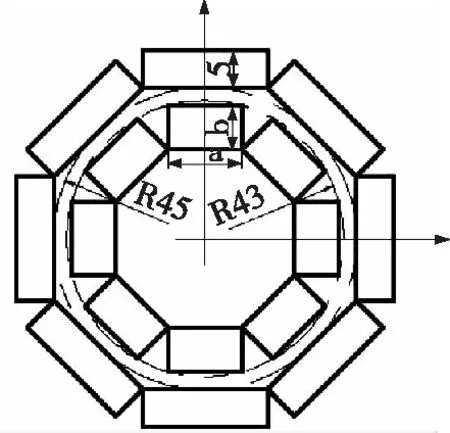
图5 内磁体参数关系

由图5可以看出内永磁体厚度越大，那么宽度则越小，为得到最佳的宽度和厚度的组合使得该联轴器具有最大传动结构，设内永磁体宽度a=2X，则厚度：

式中，m为磁极对数。

根据上述关系对内永磁体的不同尺寸进行计算得到如图6的结果。

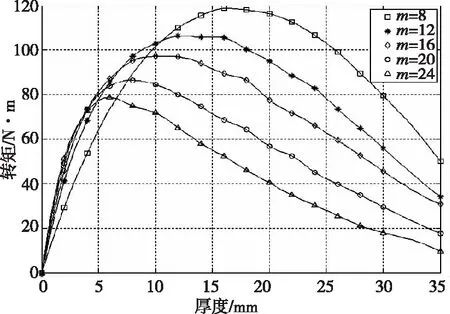
图6 内永磁体厚度对转矩的影响

由图6可知：对于每个不同磁极对数的磁力联轴器模型都存在一个最优的内永磁体宽度和厚度的组合a×b，它们分别为：21.26 mm×16 mm，15 mm×14 mm，12.9 mm×10 mm，10.98 mm×8 mm，9.67 mm×6 mm。由此可得出当内永磁体a/b的比值大约为1.33时，具有最大的传动转矩。当外永磁体为尺寸固定时，不同内永磁体下的最大传动转矩会随着磁极对数的增加而降低；产生这种现象的原因是由于磁体厚度达到一定值时，气隙磁场已饱和；此时磁极对数的增加只会带来漏磁的增加，反而降低了传动能力。同样，模型内永磁体磁体厚度的最佳值也随着磁极对数的增加而降低；这是由于磁极对数越多，气隙磁场强度越大，当同时增加磁体厚度时，磁极对数大的联轴器，其最大输出扭矩必先达到最大值。所以，对于磁极对数较大的磁力联轴器，其内永磁体厚度也相应减小。

4 优化设计

根据上述分析的结果，对磁极对数m为8、12、16的最优组合及其邻近的组合进行计算比较，进一步找出最优的结构，如表2所示。

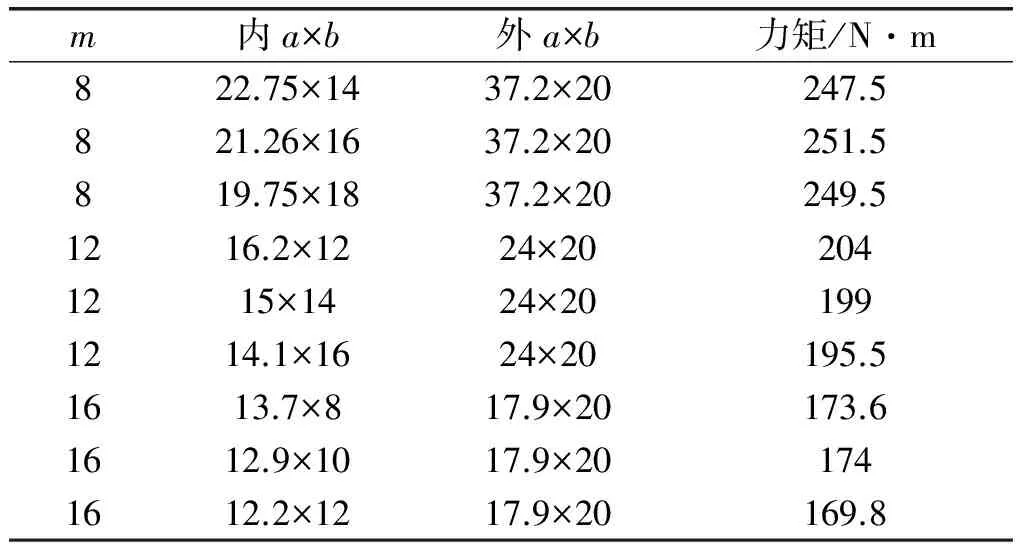
表2 优化计算结果

由表中可以看出当磁极对数为8时，磁力联轴器具有更大的传动转矩，其中m=8，外磁体为37.2 mm×20 mm，内磁体为21.26 mm×16 mm的组合是所有组合中传递转矩最大的。

5 结论

本文通过对不同尺寸的径向、切向磁力联轴器进行计算和分析得到如下结论：

1)这种磁化的磁力联轴器在内、外转子角度差为磁体排列周期的1/4时具有最大传动转矩；当磁体厚度较小，产生的气隙磁场未饱和时，不同磁极对数的联轴器，其最大转矩会随着磁极对数的增加，呈先上升后减小的趋势。

2)联轴器的最大正向转矩与最大反向转矩的比值会随着磁极对数的增加而增加。联轴器的理想工作区分布比例也随着磁极对数的增加而增加。联轴器的工作区域越宽越有利于传动，联轴器工作也越稳定，因此，一定范围内增加联轴器的磁极对数可以增宽联轴器的工作区域，以此提高联轴器工作的稳定性。

3)当内转子永磁体尺寸一定时，联轴器的传动转矩将随着外永磁体厚度的增加而增加，但增加的速率将逐渐减小；若外永磁体尺寸一定时，内永磁体尺寸将获得结构的最优，且最优组合的最大传动转矩会随着磁极对数的增加降低，磁极对数越多，内永磁体的厚度越小。

4)经过优化计算可以得出最优结构参数：m=8，外磁体为37.2 mm×20 mm，内磁体为21.26 mm×16 mm可以传递251.5 N·m的负载。

[1] G. Akoun and J. P. Yonnet .3-D analytical calculation of the forces exerted between two cuboidal magnets.IEEE Trans. Magn., vol. 20,pp. 1962-1964, Sept. 1984

[2] V. V. Fufaev and A. Y.Krasil’nikov.Torque of a cylindrical magnetic coupling.Elektro-teknika, vol. 65, no. 8, pp. 51-53, 1994

[3] F. Bancel and G. Lemarquand.Fy(theta) and fz(teta) forces between magnets.IEEE Trans. Magn., submitted for publication

[4] Charpentier J F, Lemarquand G..Optimal design of cylindrical air-gap synchronous permanent magnet couplings[J].IEEE Trans. Magn.,vol. 35, no. 2, March 1999

[5] 王玉良，孙春一.永磁联轴器的磁路结构及其特性[J].磁性材料及器件，2005(8)9-11

[6] 杨超君.鼠笼转子磁力联轴器空载气隙磁场有限元分析[J].江苏大学学报，2010，31(04)：437-441

[7] (美)亨塞尔曼(Hanselman,D)，(美)利特菲尔德(Littlefield,B)著.精通Matlab 7[M].朱仁峰译.北京：清华大学出版社，2006.5:243-247

[8] 赵博，张洪亮.Ansoft 12在工程电磁场中的应用[M].北京：中国水利水电出版社，2010.1：91-118