SBE18 pH 传感器动态特性研究*

李 冬，廖和琴，田 雨

(1.天津大学 电气与自动化工程学院，天津300072;2.国家海洋技术中心 海洋测量传感器技术研究室，天津300112)

0 引 言

由于化石燃料燃烧、森林砍伐以及其他人为因素，大气中的CO2浓度显著提高［1］。海洋吸收了1980～1994 年之间排入大气中CO2的28%～34%［2，3］。海洋表面pH 值较工业革命之前下降了0.1，预计到2100 年，海洋表层pH 还会下降0.3 ～0.5［4］。海洋酸化被认为是对海洋生物系统尤其是贝壳类和钙质类生物的主要威胁［5］。海洋层pH 测量是研究海洋酸化最重要的手段，pH 传感器的动态特性是一个重要特性，对于测量方法和测量数据处理有重要意义。

SBE18 是由美国海鸟公司推出的海洋测量研究用pH传感器。在经常标定的情况下，SBE18 pH 值测量精度能达到0.1，是海洋测量领域目前的精度最高，测量最稳定的pH 传感器之一。

CTD 传感器中温度传感器和电导率传感器动态特性一直是研究的重点［6］，pH 传感器动态响应也偶有涉及［7，8］。研究CTD 传感器动态特性时，通常将一阶系统作为传感器的动态模型，将时间常数作为传感器动态特性的参数。实际测量发现SBE18动态特性与一阶系统相差甚远，时间常数无法完全描述SBE18 的动态过程。本文提出了辨识SBE18 动态模型的方法，辨识出了SBE18 的动态模型，并分析了环境因素对传感器动态模型参数的影响。

1 传感器动态特性测试平台与测试方法

传感器动态特性测试平台槽体分为A，B 两区，中间用密封隔板隔开。两区均安装有加热器、热交换器、感应式温度电导率传感器、溶解氧传感器、pH 传感器，能分别实时监控两区水体的温度、电导率、溶解氧和pH 等参数，并能将两区水温分别控制在设定值的±0.1 ℃偏差范围内。测量装置的结构框图如图1。

图1 传感器动态响应测量平台结构框图Fig 1 Structure block diagram of sensor dynamic response measurement platform

测量前，将两区水温控制在20 ℃;分别加入适量邻苯二甲酸氢钾和硼砂缓冲剂;隔板打开后，A，B 两区水体在隔板处形成厚度为2～5 cm，pH 梯度为80～200/m 的水层，该水层是测量传感器阶跃响应的理想位置。测量时，打开密封隔板，同时传感器在驱动电机的牵引下以速度0.1，0.5，1.0，1.5 m/s 穿过pH 跃层，从A 区运动到B 区;由于该跃层厚度不能完全忽略不计，这相当于给传感器一个非理想的阶跃输入。测量过程中传感器输出信号通过电缆传递到采集板卡，采集板卡将模拟信号转换为数字信号，存储在上位机上。上位机数据处理软件计算出传感器的动态响应参数。

2 SBE18 动态特性参数测定原理

本文首先通过pH 传感器的定标公式，证明可以使用输出电压计算传感器的动态特性参数，然后给出了各阶备选模型的时域微分方程，提出给定参数条件下求解各阶模型时域微分方程的数值解法，最后阐述了使用遗传算法求解最优模型参数的方法。

2.1 SBE18 pH 传感器定标公式

SBE18 输出电压为0～5 V，其定标公式为

其中，Vout为传感器输出电压，pHoffset为pH 偏置电压，pHslope为pH 拟合斜率，K 为以开氏温标计算的环境温度，R气体常数，F 为法拉第常数。由式(1)可计算出pH 值。pHoffset，pHslope，R，F 均为常数，在一次测量过程中，A，B 两槽水体温度设为同一值，pH 值与传感器的输出电压呈线性关系，因此，本文中采用传感器输出电压—时间曲线来测定传感器的动态响应参数。

2.2 备选模型集时域微分方程

设传感器的传递函数为H(s)，传感器的输入信号为X(s)、输出信号为Y(s)，则Y(s)=H(s)·X(s)，在不考虑传感器放大系数和输入信号幅值的情况下，不妨设传感器的开环放大系数为1，即H(0)=1，则

其中，H1，H2，H3分别为一阶、二阶、三阶系统模型，τ1，τ2，τ3为其参数;t0输入信号跃变时刻，y(0)为传感器输出稳定初值，y(∞)为传感器输出稳定终值。H1，H2，H3对应的时域微分方程分别为

2.3 给定参数备选模型时域解数值解法

本文采用Bogacki-Shampine 算法求解时域微分方程。Bogacki-Shampine 方法是一种具有前后一致特性的三阶龙格库塔法，内嵌一个二阶龙格库塔法，可实现变步长计算［9，10］，在容许误差较大时，求解效果好于Dormand-Prince算法［11］。对于任意一组τ1τ2τ3t0，使用Bogacki-Shampine算法求解式(7)～式(9)，即可得到各阶模型的时域数值解yc(tc(i))，其中，tc是时间序列，yc是幅值序列。该算法的基本问题是在时间区间［t0，tf］内求解初值问题y'=F(t，y)，y(t0)=y0。Bogacki-Shampine 算法在［tn，tn+1］之间的递推公式如下

其中，yn为初值问题在tn处的数值解，hn为步长，即hn=tn+1－tn。这里，zn+1为精确解的二阶近似，yn+1为精确解的三阶近似，因此，zn+1和yn+1的差值可用作变步长。

2.4 模型误差判定

本文将模型误差分为幅值误差Ev和阶跃时刻误差Et。幅值误差Ev为传感器实际输出序列y(t(i))与模型时域数值解yc(tc(i))在时间区间［t0.05，t0.95］内的均方差和传感器输出变化幅值的比值，即

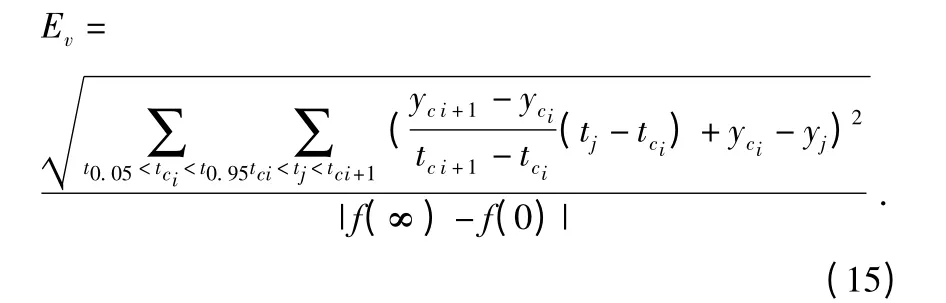
阶跃时刻误差Et为模型阶跃开始时刻t0与实际阶跃开始时刻tr0之差值的绝对值，即

其中，实际阶跃开始时刻tr0为稳定初值f(0)与实际输出曲线的最后一个交点。

2.5 备选模型最优参数优化方法

本文使用Matlab 遗传算法求解各阶系统的最优τ1τ2τ3t0［12，13］。遗传算法是一种受进化论启发的优化算法，不同于确定性求解方法，遗传算法通过受控的随机方式向最优解趋近［14］，非常适合求解空间大，峰值单一，系统模型复杂，不要求绝对全局最优的问题。

遗传算法求解的基本问题是

3 实验数据分析处理

SBE18 pH 传感器输出信号为电压信号，容易受到电磁辐射和工频交流电的干扰，本文使用软件对原始数据进行50 Hz 理想低通滤波。

3.1 最佳传感器动态模型的确定

为了评价各阶模型的适应性，对同一组传感器输出的数据分别使用各阶模型进行优化，各阶模型优化曲线与实际输出曲线进行对比如图2。评价模型优劣指标有三个，1)优化后模型的幅值误差Ev;2)优化后模型的阶跃时刻误差Et;3)模型参数数量N。Ev表征了实际输出曲线与优化曲线在取样区间内的重合度;Et表征了实际曲线与优化曲线阶跃开始时刻的差值，由于实际非理想阶跃输入的影响，该差值是必然存在的;模型参数数量N 决定了模型的复杂度，求取参数所需的时间与应用参数的难度。各阶系统适应性评价指标如表1 所示。

图2 各阶系统优化曲线与实际输出曲线对比Fig 2 Comparison of optimized curve and real output curve of each order system

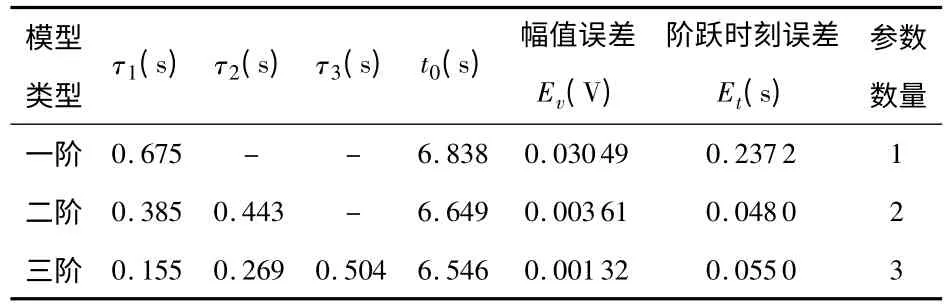
表1 使用不同传感器模型的优化结果误差Tab 1 Optimized result error of different kind of models

由以上数据分析可知，幅值误差Ev和阶跃时刻误差Et都随模型的阶数增大而减小，但模型阶数越高确定模型所需的参数N 也会越多;二，三阶模型的幅值误差Ev和阶跃时刻误差Et远小于一阶系统;三阶系统模型的幅值误差Ev略小于二阶系统，两系统的幅值误差Ev都足够小。求解复杂模型参数耗费时间多，同时复杂模型也会给使用带来不便，因此，本文将二阶系统选定为SBE18 的动态响应模型。

3.2 环境因素对模型参数的影响

实际传感器的动态特性参数不是一组固定值，它会随着传感器的使用环境改变而改变。影响pH 传感器动态特性的因素主要有两个:1)传感器的附近水流速度;2)水体pH 梯度变化方向。本文中分别在0.1，0.5，1.0，1.5 m/s 四个速度和pH 由高到低、由低到高两个方向上求取了传感器模型的参数，结果如表2 所示。

表2 不同流速和pH 变化方向下的模型参数Tab 2 Model parameters under different velocity of flow and pH change direction

随着流速增大模型参数均减小，且流速大于1.0 m/s以后传感器参数趋于稳定，因此，维持1 m/s 左右的流速有助于传感器输出快速稳定。传感器的动态参数受传感器输入信号变化方向影响十分显著，pH 值由高到低变化时，传感器的动态特性参数明显大于当pH 值由低到高变化时的数值。

4 结 论

SBE18 的参数指标里仅标明了特定流速下时间常数，没有标明该值的具体测量环境，而且时间常数也无法描述传感器的具体动态过程，这给不少相关海洋科技工作者带来很大的不便。本文深入研究了SBE18 动态参数的测量方法，分别分析了一，二，三阶系统模型对传感器动态过程的适应性，得出二阶系统模型与SBE18 动态特性符合较好;同时，求取不同流速和pH 梯度变化方下传感器二阶系统模型参数，并分析了两者对模型参数的影响。通过大量的实验数据分析得出，模型参数随流速增大而减小，且流速大于1m/s 后传感器动态特性参数趋于稳定;pH 梯度变化方向对模型参数影响大，pH 由高到低变化时传感器动态特性参数明显大于pH 由低到高时的变化。

［1］ Wootton J T，Pfister C A，Forester J D.Dynamic patterns and ecological impacts of declining ocean pH in a high-resolution multiyear dataset［C］∥Proceedings of the National Academy of Sciences，2008:18848－18853.

［2］ Millero F J.The marine inorganic carbon cycle［J］.Chemical Reviews，2007，107(2):308－341.

［3］ Sabine C L，Feely R A，Gruber N，et al.The oceanic sink for anthropogenic CO2［J］.Science，2004，305(5682):367－371.

［4］ Caldeira K，Wickett M E.Oceanography:Anthropogenic carbon and ocean pH［J］.Nature，2003，425(6956):365－365.

［5］ Caldeira K，Wickett M E.Ocean model predictions of chemistry changes from carbon dioxide emissions to the atmosphere and ocean［J］.Journal of Geophysical Research:Oceans，2005，110(C9):1978－2012.

［6］ Gregg M C，Hess W C.Dynamic response calibration of sea-bird temperature and conductivity probes［J］.Journal of Atmospheric and Oceanic Technology，1985，2(3):304－313.

［7］ Oelbner W，Zosel J，Berthold F，et al.Investigation of the dynamic response behaviour of ISFET pH sensors by means of laser Doppler velocimetry(LDV)［J］.Sensors and Actuators B:Chemical，1995，27(1):345－348.

［8］ Hara H，Ohta T.Dynamic response of a Ta2O5-gate pH-sensitive field-effect transistor［J］.Sensors and Actuators B:Chemical，1996，32(2):115－119.

［9］ Bogacki Przemyslaw，Shampine Lawrence F.A 3(2)pair of Runge-Kutta formulas［J］.Applied Mathematics Letters，1989，2(4):321－325.

［10］Shampine L F，Reichelt M W.The Matlab ode suite［J］.SIAM Journal on Scientific Computing，1997，18(1):1－22.

［11］Dormand J R，Prince P J.A family of embedded Runge-Kutta formulae［J］.Journal of Computational and Applied Mathematics，1980，6(1):19－26.

［12］Conn A R，Gould N I M，Toint P.A globally convergent augmented Lagrangian algorithm for optimization with general constraints and simple bounds［J］.SIAM Journal on Numerical Analysis，1991，28(2):545－572.

［13］Conn A，Gould N，Toint P.A globally convergent Lagrangian barrier algorithm for optimization with general inequality constraints and simple bounds［J］.Mathematics of Computation of the American Mathematical Society，1997，66(217):261－288.

［14］Child B F M，Venugopal V.Optimal configurations of wave energy device arrays［J］.Ocean Engineering，2010，37(16):1402－1417.